Des maths dans les oeuvres du peintre tchèque František Kupka.
Des tableaux fascinants
Une récente exposition au Grand Palais, à Paris, a mis en valeur les œuvres du peintre tchèque František Kupka (né le 23 septembre 1871 à Opočno en Bohême orientale, Tchéquie, et mort à Puteaux, le 24 juin 1957). Le dossier pédagogique de l’exposition-rétrospective est consultable en suivant le lien.
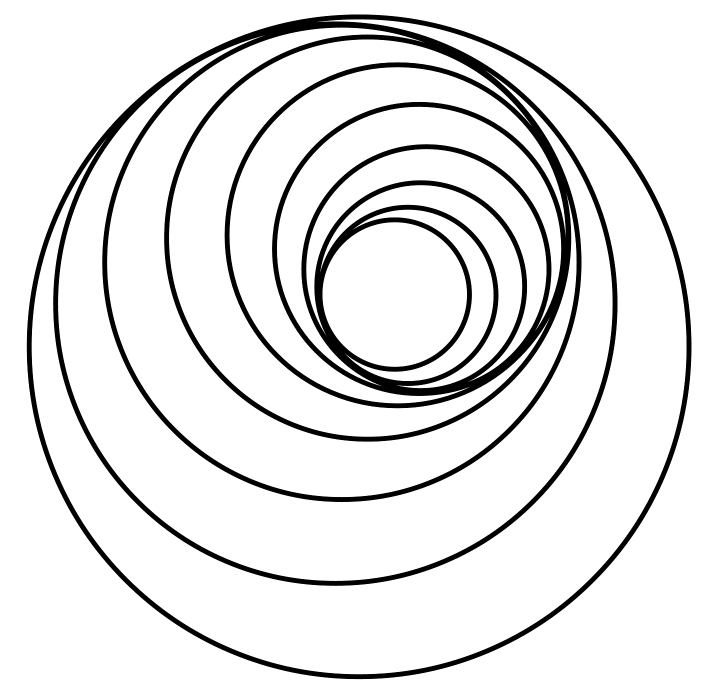
Dans la grande diversité de ses tableaux, intéressons-nous à cette « abstraction noir et blanc », peinte en 1928 et visible au musée d’art moderne du centre Pompidou à Paris.
La simplicité de cette œuvre et la disposition des cercles que nous y voyons ne peuvent qu’intriguer le mathématicien. Comment l’artiste a-t-il disposé les cercles pour produire un tel effet ?
Invitation : les illustrations de cet article sont cliquables ; les liens associés fournissant davantage d’informations sur les œuvres ou figures présentées.
Un peu de simplicité
Commençons par une situation plus simple : deux cercles. Heureusement, Kupka y a aussi pensé (ci-contre)…
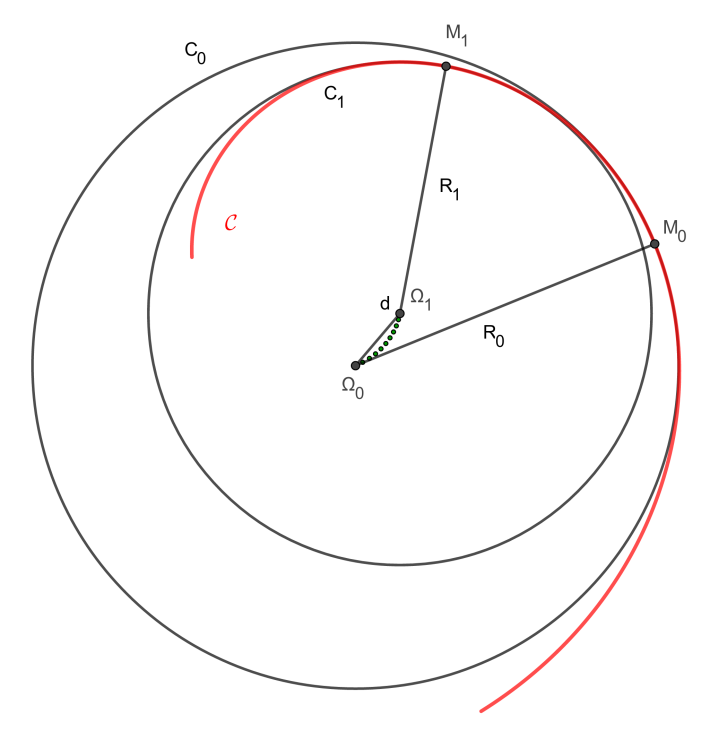
Considérons donc deux cercles \( C \) et \(C'\) du plan, de centres \(O\) et \(O'\) et de rayons \(R\) et \(R'\). On peut déjà tracer la droite \(D=(OO')\). Notons aussi \(d=d(O,O')\) la distance des deux centres.
Si les deux cercles se coupent, on peut nommer \(M\) l’un des deux points communs ; le triangle \(OMO'\) ayant des côtés de longueurs \(R\), \(R'\) et \(d\), l’inégalité triangulaire impose que chacun de ces côtés soit plus petit (au sens large) que la somme des deux autres, ce qui donne : \[ d\leq R+R',\ R\leq d+R'\Leftrightarrow R-R'\leq d,\ R'\leq d+R\Leftrightarrow R'-R\leq d \] ce qu’on peut résumer en : \[(1)\ |R-R'|\leq d\leq R+R' \]
Cet encadrement ne fait que traduire l’inégalité triangulaire pour la distance \(d\) : \[ |d(O,M)-d(M,O')|\leq d(O,O')\leq d(O,M)+d(M,O')\]
Inversement, supposons que cette inégalité ait lieu, les cercles se coupent-ils ? Pour confirmer cela, prenons un repère d’origine \(O\), de sorte que les équations de \(C\) et \(C'\) s’écrivent : \[ (2)\ \left\{ \begin{array}{l}(C)\ x^2+y^2=R^2\\(C')\ (x-d)^2+y^2=R'^2\end{array} \right. \]
Un éventuel point \(M\) commun, de coordonnées \((x,y)\), existe si, et seulement si le système (2) est vérifié. De manière équivalente, par soustraction, nous avons : \[ (2')\ \left\{ \begin{array}{c} x^2+y^2=R^2 \\ R^2+d^2-R'^2=2dx\\ \end{array} \right. \Leftrightarrow (3)\ \left\{ \begin{array}{c} x^2+y^2=R^2\\x=\frac{R^2+d^2-R'^2}{2d}\\ \end{array} \right. \]
Le système (3) revient à l’intersection du cercle \(C\) avec une droite perpendiculaire à la droite \(D\), et admet des solutions si, et seulement si la valeur de \(x\) permet de déterminer \(y\), soit encore si cette valeur vérifie \(x^2\leq R^2\). On écrit cette condition en détail : \[ (4)\ \left\{ \begin{array}{rll} R^2-R'^2+d^2\leq 2dR&\Leftrightarrow (R-d)^2\leq R'^2&\Leftrightarrow -R'\leq R-d\leq R'\\ R'^2-R^2-d^2\leq 2dR&\Leftrightarrow R'^2\leq (R+d)^2&\Leftrightarrow R'\leq R+d\\ \end{array} \right. \] ce qui revient exactement aux conditions (1) vues précédemment.
Dans le cas d’un cas d’égalité dans (1), on peut démontrer que les cercles sont tangents.
- Si \(R+R'\lt d\), les cercles sont « extérieurs » ;
- Si \(d\lt |R-R' | \), ils sont « intérieurs » l'un à l'autre.
C'est ce dernier cas qui intéresse Kupka.
Deux, trois … de nombreux cercles
Maintenant que nous savons positionner deux cercles, comment en placer une série et obtenir cet effet « tournoyant » ? Un autre tableau de Kupka va nous mettre sur la piste, avec des cercles beaucoup plus rapprochés et « presque » tangents.
En examinant ce tableau d’assez loin, l’œil « voit » une spirale à laquelle les cercles « collent ». C’est ce que nous allons préciser maintenant : comment créer des cercles qui « collent » à une courbe ?
Nous considérons donc une courbe plane \(\mathcal C\), décrite par un point \(M(s)\) dépendant d’un paramètre \(s\) variant entre 0 et \(L\)1. Le calcul différentiel va maintenant nous permettre de préciser notre questionnement ; dans la suite, nous noterons les vecteurs selon la convention internationale, en gras plutôt qu’avec des flèches. Le premier vecteur à considérer est la « vitesse » \(\frac{\mathrm d\mathbf M}{\mathrm{d}s}\) (qui dirige la tangente à la courbe au point \(M(s)\)), où le point \(M\) apparaît en gras puisque la dérivée d’un point est un vecteur2.
Pour simplifier les choses, nous allons supposer que le vecteur vitesse est unitaire ; en termes imagés, si une fourmi parcourt notre courbe de cette manière, elle avance à chaque instant en faisant 1 centimètre par seconde (si l’unité de temps est la seconde et l’unité de longueur le centimètre). De ce fait, la longueur du morceau de courbe compris entre les points \(M(s_0)\) et \(M(s_1)\) sera exactement \(s_1-s_0\)3.
Notons \(\mathbf{\tau }=\frac{\mathrm d\mathbf M}{\mathrm{d}s}\) le vecteur vitesse (tangent), et \(\mathbf{\nu}(s)\) le vecteur unitaire directement perpendiculaire à \(\mathbf{\tau}(s)\).
Pour aider le lecteur à suivre notre démarche, nous pouvons aussi considérer le cas particulier d’un cercle de rayon \(\rho\), paramétré en affixes par \(z(\theta)=\rho\mathrm e^{\mathrm i\theta},\,\theta\in\mathbb R\) ; la vitesse est en ce cas \(\frac{\mathrm dz}{\mathrm d\theta}=\mathrm iz\), de module \(\rho\) ; l’abscisse curviligne peut alors être choisie comme \(s(\theta)=\rho\theta\), amenant un nouveau paramétrage \(z(s)=\rho\mathrm e^{\mathrm i\frac s\rho}\), amenant \(\mathbf\tau=\frac{\mathrm dz}{\mathrm ds}=\mathrm i\mathrm e^{\mathrm i\theta}\) puis \(\mathbf\nu=\mathrm i\mathbf\tau=-\mathrm e^{\mathrm i\theta}\). Le vecteur normal pointe ici vers le centre du cercle, ce qui est bien … normal !
Le repère orthonormal direct \((M(s),\mathbf{\tau }(s),\mathbf{\nu }(s))\) est appelé le repère de Frenet4 au point \(M(s)\), et il « glisse » le long de la courbe quand \(s\) varie.
Nous allons maintenant chercher les dérivées de ces fonctions vectorielles de \(s\) ; en dérivant le produit scalaire5 exprimant que \(\mathbf{\tau}(s)\) est de longueur 1, nous obtenons : \[ 0=\frac{\mathrm d}{\mathrm ds}\langle \mathbf{\tau}(s)|\mathbf{\tau}(s)\rangle =\langle\frac{\mathrm d}{\mathrm ds}\mathbf{\tau}(s)|\mathbf{\tau}(s)\rangle +\langle\mathbf{\tau}(s)|\frac{\mathrm d}{\mathrm ds}\mathbf{\tau}(s)\rangle =2\langle\frac{\mathrm d}{\mathrm ds}\mathbf{\tau}(s)|\mathbf{\tau}(s)\rangle \]
Ainsi, le vecteur \(\frac{\mathrm d\mathbf{\tau }}{\mathrm{d}s}\) est perpendiculaire à \(\mathbf{\tau }(s)\) et donc colinéaire à \(\mathbf{\nu }(s)\) ; on pose ainsi \(\frac{\mathrm d\mathbf{\tau }}{\mathrm{d}s}=\gamma (s)\mathbf{\nu }(s)\) , le paramètre \(\gamma \) ainsi introduit s’appelant la courbure au point de paramètre \(s\)6. Excepté le cas embarrassant où \(\gamma(s)\) est nul (que nous éliminerons), et compte tenu du fait que \(\frac{\mathrm d\mathbf{\tau}}{\mathrm{d}s}\) est homogène à l’inverse d’une longueur7, nous pouvons poser \(\gamma(s)=\frac 1{R(s)}\) ; \(R(s)\) s’appelle le rayon de courbure au point de paramètre \(s\). En dérivant de même les égalités \(\Vert\mathbf\nu(s)\Vert^2=1\) et \(\langle \mathbf\tau(s)| \mathbf\nu(s)\rangle=0\), on trouve la formule \(\frac{\mathrm d\mathbf{\nu}}{\mathrm ds}=-\gamma(s)\mathbf{\tau}(s) % \quad,\qquad % \frac{\mathrm d^2\mathbf{\tau}}{\mathrm ds^2}=\frac{\mathrm d\gamma }{\mathrm ds}\mathbf{\nu}(s)-\gamma(s)^2\mathbf{\tau}(s) \)
Nous sommes maintenant bien équipés pour chercher un cercle qui « colle » au mieux à la courbe \(\mathcal C\) (comme le fait la tangente, mais avec une meilleure proximité grâce aux choix du centre et du rayon du cercle).
Imaginons donc un cercle de centre \(\Omega\) et de rayon \(\rho\) ; la proximité entre ce cercle et la courbe au point de paramètre \(s_0\) pourra être évaluée au moyen de la quantité \(\delta (s)=d(\Omega,M(s))^2-\rho^2\) pour \(s\) voisin de \(s_0\). Pour commencer, on va faire en sorte que \(\delta (s_0)=0\), amenant \(d(\Omega,M(s_0))=\rho\). On prend ensuite un développement limité de la fonction vectorielle \(\mathbf{\Omega M}(s)\) au voisinage de \(s=s_0\) (formule de Taylor-Young) et on le reporte dans le carré de la norme, développé en produits scalaires : \[ \begin{array}{rcl} \delta (s)&=&\Bigl\Vert\mathbf{\Omega M}(s_0)+(s-s_0)\mathbf{\tau }(s_0)+\frac 1 2(s-s_0)^2\gamma (s_0)\mathbf{\nu }(s_0)+o((s-s_0)^2)\Bigr\Vert^2-\rho^2\\ &=&2(s-s_0)\langle \mathbf{\Omega M}(s_0)|\mathbf{\tau }(s_0)\rangle+ \\ & & \hfill (s-s_0)^2\Bigl[1+ \gamma(s_0)\langle\mathbf{\Omega M}(s_0)|\mathbf{\nu}(s_0)\rangle\Bigr]+o((s-s_0)^2) \end{array} \]
Pour que cette quantité soit la plus petite possible lorsque \(s\) s’approche de \(s_0\), on prend \(\langle \mathbf{\Omega M}(s_0)|\mathbf{\tau}(s_0)\rangle =0\), ce qui revient à placer \(\Omega\) sur la normale à la courbe au point de paramètre \(s_0\), soit \(\mathbf{\Omega M}(s_0) =\lambda\mathbf{\nu}(s_0),\) \(\lambda\) étant un nombre réel restant à déterminer. Enfin, on peut faire en sorte que \(\gamma(s_0)\langle \mathbf{\Omega M}(s_0)|\mathbf{\nu}(s_0)\rangle =-1\), ce qui revient à prendre \(\lambda=\frac {-1}{\gamma(s_0)}\), soit en fin de compte : \(\mathbf{M}(s_0)\mathbf{\Omega}=R(s_0)\mathbf{\nu}(s_0)\).
En d’autres termes, la « bonne » position pour le centre du cercle se trouve en portant une longueur \(|R(s_0)|=\frac {1}{|\gamma(s_0)|}\) sur la normale et dans la direction de \(\mathbf{\nu }(s_0)\) si \(\gamma (s_0)>0\), ou dans la direction contraire sinon. Le point \(\Omega(s_0)\) ainsi défini s’appelle le centre de courbure, tandis que le cercle de centre \(\Omega(s_0)\) et de rayon \(R(s_0)\) s’appelle le cercle de courbure ou cercle osculateur8, tous relatifs au point de \(\mathcal C\) de paramètre \(s_0\).
Imitations
C’est ainsi qu’on peut produire un graphisme du genre de ceux que proposait Kupka en choisissant une courbe plane et en traçant quelques-uns de ses cercles osculateurs (régulièrement sélectionnés). Nous proposons ci-contre un tel exemple, basé sur une spirale logarithmique, en invitant le lecteur à se persuader du fait que cette figure n’est formée que de cercles, sans aucune courbe supplémentaire. L’artiste a utilisé d’autres spirales, bien à lui, comme nous le suggère cette œuvre Abstrakče XI faisant partie d’une brochure publiée en 1933…
Le secret final
Il nous reste à expliquer pourquoi les cercles osculateurs associés à une spirale (ou toute courbe dont la « courbure » varie de manière strictement monotone) sont « imbriqués » les uns dans les autres. Pour simplifier, nous supposerons désormais que la fonction \(s\mapsto\gamma(s)\) associée à la courbe \(\mathcal C\) est positive et strictement croissante. Examinons comment le centre de courbure \(\Omega(s)=M(s)+R(s)\mathbf\nu(s)\) se déplace quand \(s\) varie1 : \[ \frac{\mathrm d\mathbf{\Omega}}{\mathrm{d}s}=\frac{\mathrm d\mathbf M}{\mathrm{d}s}+\frac{\mathrm dR}{\mathrm{d}s}\mathbf{\nu}(s)+R(s)\frac{\mathrm d\mathbf{\nu }}{\mathrm{d}s} =\mathbf{\tau }(s)+\frac{\mathrm dR}{\mathrm{d}s}\mathbf{\nu }(s)-\mathbf{\tau }(s)=\frac{\mathrm dR}{\mathrm{d}s}\mathbf{\nu}(s) \]
Si nous considérons une portion de la courbe initiale \(\mathcal C\), obtenue pour \(s\) variant de \(s_0\) à \(s_1\), la longueur de la trajectoire décrite par \(\Omega\) est \[\int_{s_0}^{s_1}\Bigl\Vert\frac{\mathrm d\mathbf\Omega}{\mathrm{d}s}\Bigr\Vert\mathrm{d}s =\int_{s_0}^{s_1}\Bigl|\frac{\mathrm dR}{\mathrm{d}s}\Bigr|\mathrm{d}s=R(s_0)-R(s_1) \] parce qu’ici la fonction \(s\mapsto R(s)\) est décroissante.
Cependant, la longueur de l’arc de la courbe décrit par \(\Omega\) est au moins égale à la longueur de la corde qui le sous-tend, c’est-à-dire à la distance entre les deux centres \(\Omega(s_0)\) et \(\Omega(s_1)\). Cette inégalité s’écrit \(d(\Omega(s_0),\Omega(s_1))\leq R(s_0)-R(s_1)\), exprimant précisément que le cercle osculateur au point de paramètre \(s_1\) est « à l’intérieur » du cercle osculateur au point de paramètre \(s_0\).
En guise de conclusion
Les cercles osculateurs, tels que nous les avons découverts, jouent aussi un rôle dans toutes sortes d’applications : en mécanique bien sûr, mais aussi pour esquisser le tracé d’un ellipse en quatre coups de compas :
C’est ici que s’achève ce parcours autour de quelques-unes des œuvres abstraites de Kupka, qui nous a amenés à exercer notre regard, passant de l’observation à la compréhension, aboutissant à une exploration attentive d’un aspect aujourd’hui peu connu de la géométrie différentielle ; n’est-ce pas ce à quoi l’œuvre d’art comme celle de la nature nous invitent de manière plus générale, nous interpellant constamment pour peu que nous sachions manifester notre curiosité ?
Références :
[1] Bibm@th.net, Biographie de Jean-Frédéric Frénet
http://www.bibmath.net/bios/index.php?action=affiche&quoi=frenet
[2] Wikipedia, Article sur le cercle osculateur
https://fr.wikipedia.org/wiki/Cercle_osculateur
[3] Publimath, Fiche bibliographique sur le cercle osculateur
http://publimath.irem.univ-mrs.fr/publimath.php?r=cercle+osculateur&b=biblio&affichage=20
[4] Accromath, Virer sans déraper (automne 2014). Article introductif sur la courbure et les cercles osculateurs.
http://accromath.uqam.ca/2014/10/virer-sans-deraper
[5] Gottfried Wilhelm Leibniz, Meditatio nova de natura anguli contactus et osculi…
Reproduction fournie par Gallica (BnF)
Documents à télécharger
Texte au format PDF à imprimer ou à sauvegarder