La compétence « Développer – Factoriser » est ancrée dès l'école primaire 1 sur des exemples numériques au moment de poser la multiplication. Les stratégies mentales sont expliquées aux élèves avec des cas génériques, que ce soit pour calculer le produit \begin{equation} 45 \times 21 = 45 \times (20+1),\label{dev3}\end{equation} d'abord décomposé en la somme  $45 \times 20 + 45 \times 1$ ou pour calculer le produit $6 \times 18 = 6\times (20-2)$, d'abord transformé en la différence $6 \times 20 - 6 \times 2$ ou encore pour calculer la somme $23 \times 7 + 23 \times 3$, d'abord ramassée en le produit $23 \times(7+3) = 23 \times 10$.  Cependant, aucune théorie n'est exposée à ce stade. C'est véritablement au collège 2 que des premières propriétés sont édifiées dans le registre littéral, à travers les deux formules, à lire dans les deux sens, \begin{equation} {\color{red}k}({\color{blue}a} + {\color{brown}b})={\color{red}k}{\color{blue}a} + {\color{red}k}{\color{brown}b} \label{dev1} \end{equation} \begin{equation} {\color{red}k}({\color{blue}a} - {\color{brown}b}) = {\color{red}k}{\color{blue}a} - {\color{red}k}{\color{brown}b} \,, \label{dev2} \end{equation} formules que l'on peut résumer en la seule identité (\ref{dev1}) si l'on autorise ${\color{blue}a}$ et ${\color{brown}b}$ à être positifs ou négatifs.

Des codes couleur ont ici été utilisés afin de mieux suivre les rôles de chaque terme. On notera aussi que, dans un souci de place, les symboles $\times$ de multiplication sont été omis ; on veillera à ce que ce raccourci ne brouille pas les calculs pratiques. Ainsi ne confondra-t-on pas l'écriture $45\times 20 + 45\times 1$ issue de (\ref{dev3}) avec la somme $4\,520+451$  !

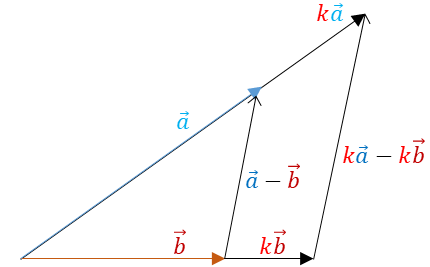
La formule (\ref{dev1}) sera étendue au lycée 3. D'une part, on y verra le paquet délimité par les parenthèses contenir des vecteurs. La réciproque du théorème de Thalès sera ainsi merveilleusement compilée dans cette phrase essentielle, \[ {\color{red}k}(\color{blue}{\vec{a}} -\color{brown}{\vec{b}})={\color{red}k}\color{blue}{\vec{a}} - {\color{red}k}\color{brown}{\vec{b}} \,,\]qu'illustre la figure 1. 

D'autre part, plusieurs facteurs pourront faire somme, ce qui donnera naissance à un paquet de tête dans le membre de gauche, et à la formule connue sous le nom de double distributivité :\begin{equation} ({\color{red}k}+{\color{green}\ell})({\color{blue}a} + {\color{brown}b}) = {\color{red}k}{\color{blue}a} + {\color{red}k}{\color{brown}b} +{\color{green}\ell}{\color{blue}a} + {\color{green}\ell}{\color{brown}b}  .\label{dev4} \end{equation}

L'usage veut qu'on présente le membre de droite de (\ref{dev4}) dans l'ordre lexicographique (comme dans un dictionnaire, le « mot » $k a$ est situé avant $k b$, lui-même avant $\ell a$, etc.), et qu'on ne joue pas immédiatement de la commutativité du produit (on ne remplace pas tout de suite $k a$ par $a k $ par exemple). Ceci permet de bien lister les combinaisons de lettres sans en oublier, surtout quand il y a davantage de paquets, comme sur les égalités plus générales $(k+\ell+\cdots)(a+b+\cdots) = ka + kb +\cdots+\ell a + \ell b + \cdots$

voire $(\alpha+\beta+\cdots)(k+\ell+\cdots)(a+b+\cdots)=\alpha k a + \alpha k b + \cdots$ .

Nous allons maintenant réinterpréter les relations (\ref{dev1}) et (\ref{dev4}) en nous aidant d'un facteur, au sens d'un postier, qui ferait sa tournée.

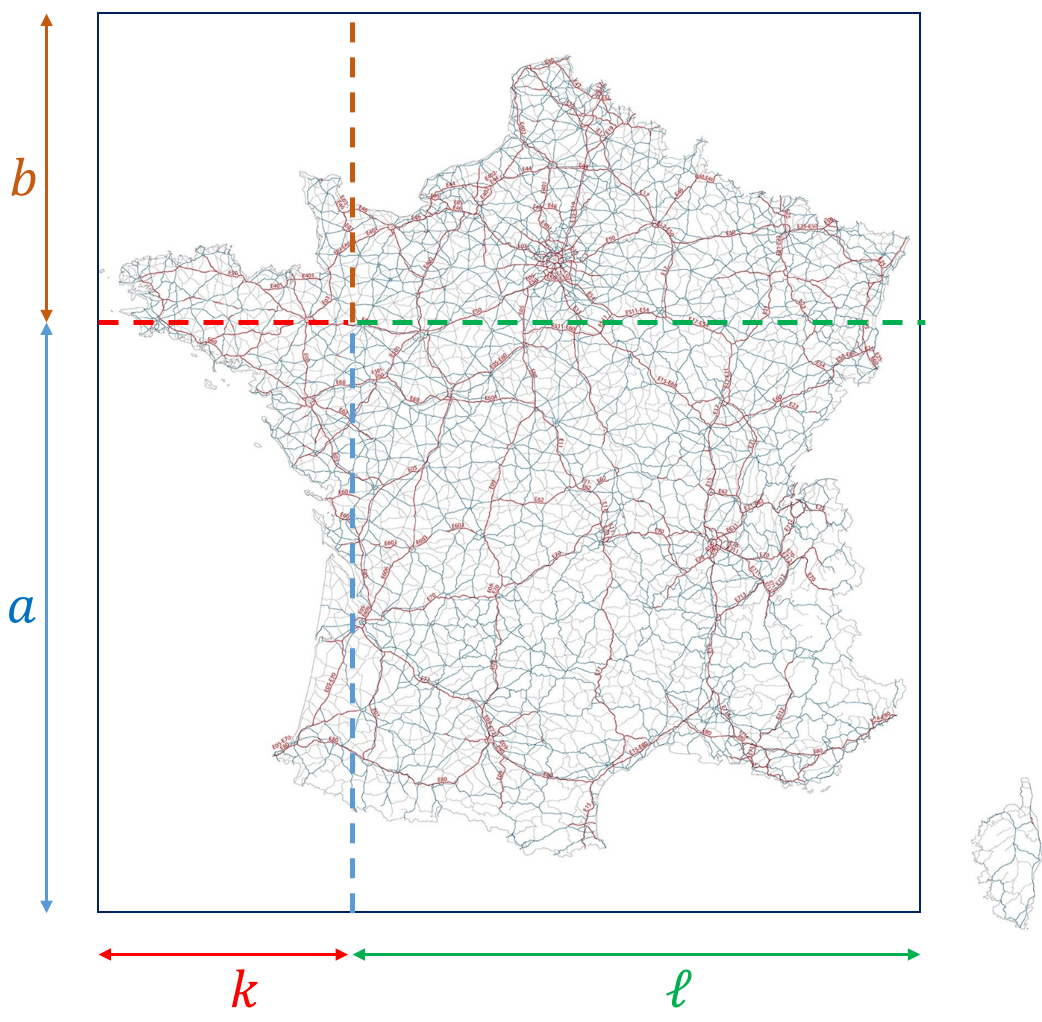
Le facteur a d'abord besoin d'une carte routière pour planifier son trajet. Celle de la figure 2, au format $({\color{red}k}+{\color{green}\ell})\times ({\color{blue}a} + {\color{brown}b})$ est déjà prédécoupée en quatre petits rectangles issus de son dépliage (selon les traits). Leurs aires, qui valent respectivement à ${\color{red}k}{\color{blue}a}$, ${\color{green}\ell} {\color{blue}a}$, ${\color{red}k}{\color{brown}b}$, ${\color{green}\ell} {\color{brown}b}$, s'assemblent en l'aire totale de valeur $({\color{red}k}+{\color{green}\ell})\times ({\color{blue}a} + {\color{brown}b})$. Ainsi, \[ ({\color{red}k}+{\color{green}\ell})\times ({\color{blue}a} + {\color{brown}b}) = {\color{red}k}{\color{blue}a} +{\color{green}\ell}{\color{blue}a} + {\color{red}k}{\color{brown}b} + {\color{green}\ell}{\color{brown}b} \, \] ce qui rend bien compte de l'identité (\ref{dev4}).

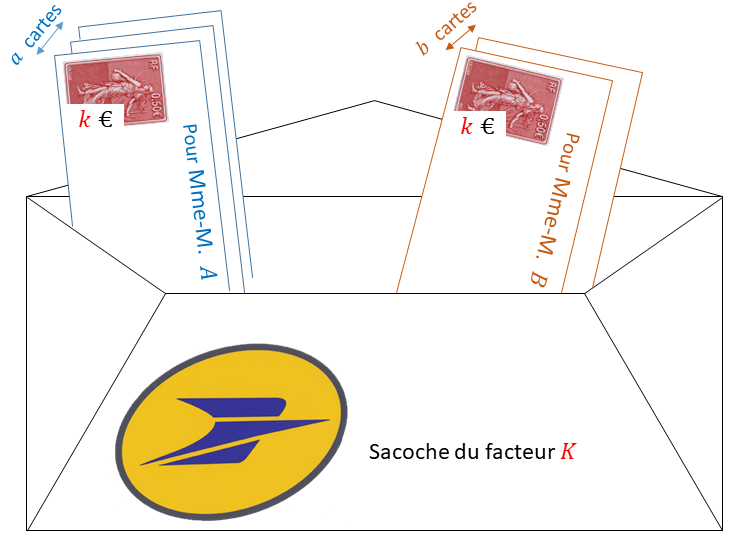
Jouons ensuite sur les mots : après les cartes routières, faisons place aux cartes postales et exploitons le lexique décrivant (\ref{dev1}) et (\ref{dev4}), qui ne doit certainement rien au hasard. Ceci va nous permettre quelques analogies, et nous offrir de nouvelles images. En effet, dans la formule (\ref{dev1}) lue de gauche à droite, le facteur ${\color{red}k}$ se distribue tour à tour sur les nombres ${\color{blue}a}$ et ${\color{brown}b}$. Dans ce processus de DÉVELOPPEMENT, la parenthèse – l'enveloppe donc – est décachetée. On passe alors insensiblement du registre mathématique au registre postal. Un peu comme si le facteur (appelons-ce messager ${\color{red}K}$) distribuait au gré de sa tournée et après les avoir extraites de sa sacoche – une grande ENVELOPPE donc – des cartes postales aux adresses d'un premier destinataire (appelons-le ${\color{blue}A}$) puis d'un second (appelons-le ${\color{brown}B}$) : ${\color{blue}a}$ cartes pour ${\color{blue}A}$, ${\color{brown}b}$ cartes pour ${\color{brown}B}$, chacune affranchie au tarif de ${\color{red}k}$ euros, figure 3.

Mais La Poste peut organiser deux tournées quotidiennes au lieu d'une (ce fut le cas jusqu'en 1983). Le service est (était ?) meilleur. Ceci justifie une majoration, mettons de ${\color{green}\ell}$ euros, figure 4, qui débouche sur le calcul de \[ ({\color{red}k}+{\color{green}\ell})({\color{blue}a} + {\color{brown}b}) \] égal à \[ ({\color{red}k}+{\color{green}\ell}) {\color{blue}a} + ({\color{red}k}+{\color{green}\ell}){\color{brown}b} \] et donc, en revenant aux achats effectués par chaque expéditeur, \[ {\color{red}k}{\color{blue}a} +{\color{green}\ell}{\color{blue}a} + {\color{red}k}{\color{brown}b} + {\color{green}\ell}{\color{brown}b} \,. \] La commutativité de l'addition réordonne cette somme comme en (\ref{dev4}).