L'ensemble $\mathbb{C}$ : premier volet d'un diptyque consacré aux nombres complexes, de leur introduction à leur utilisation au lycée.
Introduits en classe de première technologique (spécialité physique-chimie et mathématiques en STI2D 1) et, dans la voie générale, en classe de terminale (option mathématiques expertes 2), les nombres complexes y font l'objet d'une double approche : algébrique d'une part, géométrique d'autre part. De fait, c'est à l'époque de la Renaissance italienne que les complexes ont été « imaginés » pour résoudre dans $\mathbb{R}$ et via leur détour un problème d'algèbre pure : celui des équations du troisième degré 3. Et ce n'est qu'au XIXe siècle que l'Histoire leur accorda le statut de nombres de plein titre – et plus seulement d'anomalie, quand on su les interpréter géométriquement. D'un point de vue pédagogique, dissocier les deux entrées, algébrique et géométrique, pourrait cependant priver l'ensemble $\mathbb{C}$ d'une partie de son sens. Essayons ici de réconcilier la définition des lois qui le gouvernent avec les propriétés qu'on est en droit d'en attendre.
Définition des complexes...
Comment enseigner les nombres complexes ? Car on ne sait pas bien où donner de la tête. En effet,
- faut-il les définir comme un sous-espace de $\mathcal{M}_2(\mathbb{R})$ ?
- faut-il adopter la vision algébrique du corps de rupture de $X^2+1$ ?
- faut-il parachuter un nouvel élément, $\mathrm{i}$, qui cohabitera avec les réels tout en vérifiant certaines règles de calcul qui lui seraient propres ?
- faut-il les introduire en équipant $\mathbb R^2$ d'une loi multiplicative « tirée du chapeau » ?
Rigoureuses mais abstraites, les deux premières approches s'adressent à un public assez avancé. Quand les deux suivantes paraîtraient dogmatiques : de quel « chapeau » sort ce nombre « imaginaire », $\mathrm{i}$ ? Quant à cet étrange produit, $$(x,y)\times(x',y')=(xx'-yy',xy'+yx')\; ,$$ pour quelle raison serait-il associatif ? Enfin, quid des inversibles ? Il subsistera beaucoup de frustration pour un lycéen curieux qui voudrait dépasser la sentence au ton catégorique « on pose... et c'est comme ça !».
Alors pourquoi ne pas partir de la géométrie du plan euclidien ? Les objets y sont tangibles, les opérations concrètes, l'environnement familier. Le nombre réel $x$ s'identifie naturellement au point $M(x,0)$ de l'axe des abscisses ainsi qu'au vecteur horizontal de coordonnées $(x,0)$. L'addition de deux nombres réels $x$ et $x'$ revient à translater du vecteur $(x,0)$ le point $(x',0)$. Et, pourvu que $x$ ne soit pas nul, leur produit à appliquer l'homothétie de centre $O$ et de rapport $x$ au point $(x',0)$. Ainsi s'agit-il d'étendre au plan tout entier ces opérations en usant de transformations identiques voire un peu plus générales. Ceci garantirait cohérence et compatibilité : les opérations encore réalisées sur l'axe des abscisses resteraient inchangées et les autres, bien que plus « complexes », leur ressembleraient.
... par la géométrie
Risquons-nous donc, sans prétention ! Plaçons-nous dans le plan muni de son repère canonique $(O,\overrightarrow{\imath},\overrightarrow{\jmath})$ avec $OI=\overrightarrow\imath$ et $OJ=\overrightarrow\jmath$. Nous connaissons bien certaines transformations élémentaires :
- les translations d'une part. Pour un point $M$, on note $\tau_{M}$ la translation de vecteur $\overrightarrow{OM}$ ;
- les rotations et les homothéties centrales (par défaut, de centre $O$), d'autre part. On note $r_\varphi$ la rotation centrale d'angle $\varphi\in\mathbb R$ et $h_\lambda$ l'homothétie centrale de rapport $\lambda\ne 0$.
Que savons-nous de ces transformations ?
- elles sont bijectives ;
- les rotations centrales et les homothéties centrales commutent. Leur composée est qualifiée de similitude directe, et toute homothétie $h_x$ de rapport $x\lt 0$ s'apparente à la similitude de rapport (de similitude) $x\gt 0$ et d'angle de mesure $\pi$ ;
- $r_{\varphi}\circ r_{\varphi'}=r_{\varphi+\varphi'}$ et $h_{\lambda}\circ h_{\lambda'}=h_{\lambda\lambda'}$ ;
- $h_\lambda\circ r_{\varphi}\circ \tau_M=\tau_{h_\lambda\circ r_\varphi(M)}\circ h_\lambda\circ r_\varphi$, ce qu'illustre le schéma de la figure 1 ci-après.
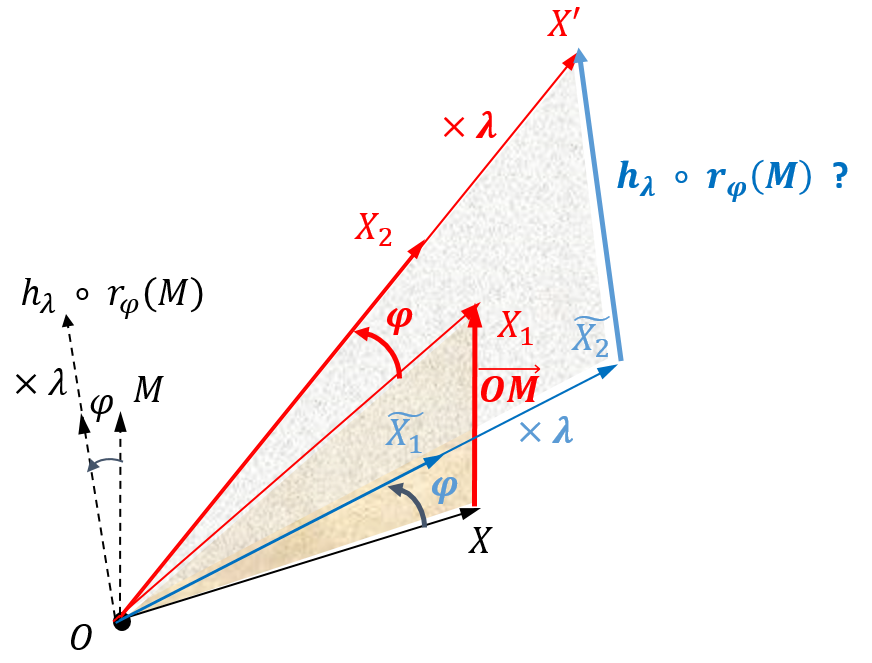
D'une part, $X \xrightarrow{\tau_{M}} X_1 \xrightarrow{r_\varphi} X_2 \xrightarrow{h_\lambda} X'$ et d'autre part $X \xrightarrow{r_\varphi} \widetilde{X_1} \xrightarrow{h_\lambda} \widetilde{X_2}$. Les triangles en surimpression $OXX_1$ et $O\widetilde{X_2}X'$ sont semblables. Donc $\widetilde{X_2}\xrightarrow{\tau_{h_\lambda \circ r_\varphi(M)}} X'$. Si bien que les deux enchaînements $h_\lambda\circ r_{\varphi}\circ \tau_M(X)$ et $\tau_{h_\lambda\circ r_\varphi(M)}\circ h_\lambda\circ r_\varphi(X)$ mènent au même point : $X'$.
Comment, dès lors, additionner $M$ et $M'$ ? En adoptant tout bonnement le modèle réel, soit $$M+M'=\tau_{M}(M').$$ On se convainc, crayon et papier en main, de la commutativité et de l'associativité de cette loi ainsi que de la neutralité de l'élément $O$ et de l'existence d'un opposé à chaque point.
Et comment multiplier $M \ne O$ et $M'$ ? En adaptant tout simplement le modèle réel, soit : $$M\times M'=h_M(M')$$ où l'on interprète « l'homothétie centrale de rapport $M$ » comme la similitude centrale de rapport (de similitude) $\lambda=OM$ et d'angle orienté $\varphi=(\overrightarrow\imath,\overrightarrow{OM})$. En d'autres mots, $h_M=h_{\lambda}\circ r_{\varphi}$. Si bien que : \[M\times M'=h_\lambda\circ r_\varphi(M').\] On remarque que $M\times M'=h_{\lambda}\circ r_\varphi\circ h_{\lambda'}\circ r_{\varphi'}(I)=h_{\lambda\lambda'}\circ r_{\varphi+\varphi'}(I)$; ce qui nous donne presque gratuitement la commutativité, l'associativité ainsi que l'inversibilité des points autres que $O$. Enfin, on vérifie que \begin{align*} M\times(M'+M'')&=h_{\lambda}\circ r_{\varphi}(M'+M'')=h_{\lambda}\circ r_{\varphi}\circ\tau_{M'}(M'')\\&=\tau_{h_{\lambda}\circ r_{\varphi}(M')}(h_{\lambda}\circ r_{\varphi}(M''))=h_{\lambda}\circ r_{\varphi}(M')+h_{\lambda}\circ r_{\varphi}(M'')\\&=M\times M'+M\times M'', \end{align*} et voici démontrée la distributivité à gauche, celle de droite découlant de la commutativité.
Certes, mais en pratique, comment construire géométriquement le produit $M\times M'$ ? On le sait égal au point $P(p,q)$ obtenu en faisant tourner $M'$ de l'angle orienté $\varphi = (\vec{\imath},\overrightarrow{OM})$ que le vecteur $\overrightarrow{OM}$ forme avec l'axe des abscisses, tout en coefficientant, chemin faisant, le vecteur $\overrightarrow{OM'}$ par la longueur $OM$. Une façon élémentaire d'y parvenir, sans composer explicitement rotation et homothétie, consiste à reproduire le triangle rectangle de sommets $O$, $x$, $M$ :
- en le posant sur le vecteur $\overrightarrow{OM'}$...
- ... mais en choisissant pour unité de référence la longueur $OM'$, ceci correspondant à un changement d'échelle...
ce que nous résumons dans le schéma très fonctionnel ci-dessous en figure 2.
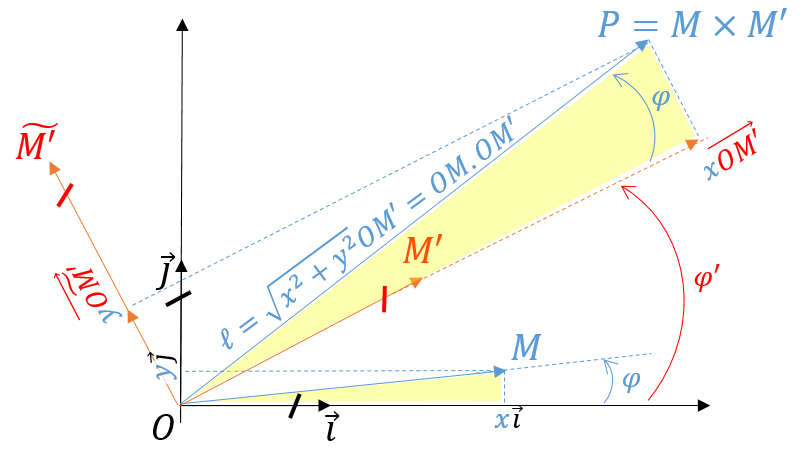
La construction du produit $P(p,q)$ des deux complexes $M(x,y$) et $M'(x',y')$ utilise le point auxiliaire $\widetilde{M'}=r_{O,\frac{\pi}{2}}(M')$. On notera que les triangles en surimpression, de sommets $O$, $x$, $M$ d'une part et $O$, $xM'$, $P$ d'autre part, sont semblables.
Quand $M(x,0)$ et $M'(x',0)$ occupent l'axe des abscisses, cette version restitue bien le produit $xx'$ habituel, y compris dans les cas d'école où
- $x$ serait nul. L'angle $\varphi$ n'a pas de valeur précise mais, $OM$ étant nul, la pondération du vecteur $\overrightarrow{OM'}$ par $0$ ramène au point $O$;
- $x$ serait négatif, dans la mesure où, dès lors, $\varphi = \pi$.
Expression algébrique du produit dans $\mathbb{R}^2$
Le calcul analytique de la somme $S=M+M'$ tombe immédiatement puisque pour $M(x,y)$ et $M'(x,y)$, \begin{align}\label{addition} M+M'(x+x',y+y'). \end{align}
Le calcul analytique du produit $P=M\times M'$ est un peu plus délicat. Notons à cet endroit qu'une définition « naturelle » de ce produit, naïvement calquée sur l'addition, conduirait à poser $M\star M'(xx',yy')$ mais ôte à l'opération toute chance d'intégrité. Nous aurions par exemple $I\star J=O$ tandis que $I\neq O$ et $J\neq O$, ce qui finalement ne serait pas si « naturel » que cela...
Revenons à notre produit $P=M\times M'$ tel que défini géométriquement en section 2, et dont l'expression analytique dérive aisément de la figure 2. Le vecteur $\overrightarrow{O\widetilde{M'}}$ naît de la rotation d'angle droit et direct du vecteur $\overrightarrow{OM'}(x',y')$, il a donc pour coordonnées $(-y',x')$. Comme \[ \overrightarrow{OP}\left\lvert \begin{matrix} p\\ q \end{matrix} \right. =x\;\overrightarrow{OM'} \left\lvert \begin{matrix} x'\\ y' \end{matrix} \right. + y\;\overrightarrow{O\widetilde{M'}} \left\lvert \begin{matrix} -y'\\ x' \end{matrix} \right. \] il vient sans subterfuge $p=xx'-yy'$ et $q=xy'+yx'$, et donc \begin{equation} \label{multiplication2} P(xx'-yy',xy'+yx') = M \times M'. \end{equation}
Voilà qui légitime une formule surgissant parfois des livres comme par « magie ». En plus d'induire la multiplication usuelle sur $\mathbb{R}$ (confondu avec $\mathbb{R} \times \{0\}$ ainsi qu'il a été expliqué plus haut), cette expression renoue sans surprise avec la loi dite du « produit externe » de multiplication par un scalaire où, quand $\lambda = (\lambda,0)$ est un simple réel, \begin{equation} \label{multiplication_externe} \lambda \times (x,y) = (\lambda x, \lambda y). \end{equation} Distribuer le facteur $\lambda$ sur les coordonnées $x$ et $y$ met ainsi en œuvre l'homothétie centrale de rapport (algébrique) $\lambda$ sur le point $M(x,y)$.
L'animation en JavaScript/JSXGraph réalisée pour la circonstance offre un rendu dynamique de la multiplication complexe. En option, on pourra assujettir multiplicande et multiplicateur à un axe ou à un cercle, ce qui revient à ne composer que par une rotation ou une homothétie.
Conjugaison et inverse
Si $M$ est un point non nul, avec $\lambda = OM$ et $\varphi=(\overrightarrow\imath,\overrightarrow{OM})$ dans la lignée des conventions d'écriture ci-dessus, notons $\overline M=r_{-2\varphi}(M)$, l'image de $M$ par la symétrie axiale selon l'axe des abscisses. Remarquons que $\overline O=O$. En termes de coordonnées, nous déduisons de $M(x,y)$, $\overline M(x,-y)$, ce qui implique $\overline{M+M'}=\overline M+\overline{M'}$.
Par ailleurs, $\overline I=I$, comme chez tout autre élément de l'axe des abscisses, si bien que \[\overline{M\times M'}=\overline{r_{\varphi+\varphi'}\circ h_{\lambda \lambda'}(I)}=r_{-\varphi-\varphi'}\circ h_{\lambda \lambda'}(I)=\overline M\times \overline {M'}\].
Par suite et pour $M$ non nul, $M\times \overline M=h_{\lambda^2}(I)=OM^2$ si bien que : \[\frac{1}{M}=\frac{\overline{M}}{OM^2}=(\frac{x}{x^2+y^2},\frac{-y}{x^2+y^2}).\]
En découle la structure de corps du plan $\mathbb{R}^2$ muni des lois $+$ et $\times$ qui lui sont dévolues.
L'ensemble $\mathbb{C}$
L'ensemble $\mathbb{C}$ des complexes n'est jamais que le nom attribué au produit cartésien $\mathbb{R}^2$ structuré par les lois $+$ et $\times$ ci-dessus.
Pour être (presque) tout à fait complet, il faut encore fixer une convention. Le complexe générique $z=(x,y)$ se décompose en vertu de (\ref{addition}), de (\ref{multiplication_externe}) et de la commutativité du produit en \begin{align*} z &= (x,y)\\ &=(x,0)+(0,y)\\ &=x(1,0)+y(0,1)\\ &=x(1,0)+(0,1)y \end{align*} On identifie $(1,0)$ et $1$ comme ci-dessus. On pose alors traditionnellement \[\mathrm{i} = (0,1)\] si bien que \begin{equation} z = x\;+\;\mathrm{i}y \end{equation} et que, géométriquement (méthode à préférer, la composée de deux rotations d'angle droit et direct donnant une symétrie centrale) ou par le calcul (méthode moins intuitive)... \begin{equation} \mathrm{i}^2= -1. \end{equation}
Refermons ce premier volet consacré aux complexes en signalant que leur ensemble $\mathbb{C}$ peut être muni d'une relation d'ordre totale. Pour classer $(x,y)$ et $(x',y')$, on peut comparer d'abord $x$ à $x'$ et, en cas d'égalité, $y$ à $y'$. Il s'agit là de l'ordre dit lexicographique, celui du dictionnaire réduit aux mots de deux lettres (ou digrammes). Cet ordre prolonge à $\mathbb{C}$ celui déjà en vigueur dans $\mathbb{R}$. Il n'est cependant pas compatible avec la multiplication par des complexes positifs. Ainsi a-t-on \begin{equation} 0<\mathrm{i} \end{equation} mais, contrairement au cas des réels positifs, cette inégalité ne se multiplie pas à elle-même, sans quoi aurions-nous \begin{equation} 0<\mathrm{i}^2=-1. \end{equation} Plus généralement, on montre qu'il n'existe aucun ordre sur $\mathbb C$ compatible avec la multiplication pour les éléments positifs : on dit que le corps $\mathbb C$ n'est pas ordonnable.