Un mesurage présente en général des imperfections qui occasionnent une erreur pour le résultat de mesure. On envisage traditionnellement qu’une erreur possède une composante aléatoire et une composante systématique.
Introduction
Dans les programmes de Terminale S de physique-chimie le problème des incertitudes lors de mesures de grandeurs a pris une nouvelle importance. La manière ancienne de donner un résultat de mesure avec une incertitude absolue, qui n’était plus utilisée, a été remplacée par une approche probabiliste des erreurs inhérentes à un processus de mesurage. En cela, le programme se met en accord avec les recommandations du Bureau International des Poids et Mesures et avec les pratiques industrielles.
Dans le guide publié par le BIPM en 2008 connu sous l’appellation de GUM (Guide to the expression of Uncertainty in Measurement) on peut lire en introduction :
« Un mesurage présente en général des imperfections qui occasionnent une erreur pour le résultat de mesure. On envisage traditionnellement qu’une erreur possède une composante aléatoire et une composante systématique. »
Les causes de la composante systématique de l’erreur peuvent en général être identifiées et corrigées, comme par exemple la dérive d’un instrument de mesure.
En revanche, la composante aléatoire ne peut pas être supprimée et il est donc important d’évaluer sa dispersion. L’outil naturellement utilisé est l’écart-type car il permet d’exprimer le résultat d’une mesure à l’aide d’un intervalle de confiance.
L’objet de cet article est de donner les éléments pour comprendre l’intérêt de cette nouvelle approche du problème des erreurs.
Bref historique
On mesure depuis très longtemps des grandeurs mais l’étude de l’incertitude associée est assez récente.
Au XVIIIe siècle une préoccupation majeure est la forme de la Terre. Newton avait conjecturé qu’elle est aplatie aux pôles. Pour le vérifier deux expéditions sont menées en 1735 et 1736 : une en Laponie par Maupertuis l’autre au Pérou par La Condamine, Godin et Bouguer afin de comparer les mesures d’un arc de méridien. Les mesures se font par la méthode de la triangulation et la seule méthode envisagée pour réduire l’incertitude est de procéder de la manière la plus précise possible.
Pour une portion que La Condamine et Bouguer avaient mesurée séparément les séries de chiffres étaient légèrement différentes. La Condamine, qui n’est pas mathématicien, suggère à Bouguer, qui lui l’est, de faire la moyenne arithmétique. Bouguer réfutera cette méthode avec hauteur et préférera faire une troisième série.
En 1791 Delambre et Méchain sont chargés par la Constituante de monter une expédition en vue de mesurer l’arc de méridien entre Dunkerque et Barcelone dans le but de définir la nouvelle unité universelle de longueur, le mètre, comme la dix-millionième partie d’un quart de méridien. Ils vont utiliser pour cela le cercle répétiteur de Borda (photo ci-dessous) qui permet de mesurer $n$ fois le même angle sans revenir à zéro. Pour obtenir la mesure de l’angle on divise par $n$ : Bouguer n’est plus là pour protester…
Il semble évident à l’époque que l’incertitude est divisée par $n$.
Un peu plus tard Gauss, passionné d’astronomie, se pose la question des erreurs de mesure et montre que la loi normale, déjà découverte comme loi-limite par Laplace, joue un rôle central dans l’évaluation des erreurs (Parzysz, 2013).
Les incertitudes à l’ancienne
Il y a encore une vingtaine d’années tous les cours de physique débutaient par un indigeste « calcul des incertitudes ». Le principe de départ était très simple : on encadre chaque valeur mesurée par les extrêmes supposés qu’elle peut atteindre ce qui se notait
\[x\pm \Delta x\]
On exposait ensuite un certain nombre de règles de composition des incertitudes dont celle-ci : l’incertitude (absolue) sur la somme ou la différence de deux grandeurs est la somme des incertitudes :
$$\Delta (x+y)=\Delta x+\Delta y$$
Pour comprendre en quoi cette méthode n’était pas précise, prenons le cas du cercle de Borda.
Supposons que l’on ait fait une série de n mesures du même angle \[{{x}_{1}},...,{{x}_{n}}\] Chacune d’elle est obtenue par des visées et donc comporte la même incertitude. Le cercle permet d’obtenir la mesure de la somme de n angles avec une seule lecture sur le cercle donc une seule incertitude e à ce moment.
Une évaluation de la mesure de l’angle sera donc \[x=\frac{1}{n}\left( \sum\limits_{k=1}^{n}{{{x}_{k}}}+e \right)\]
Un calcul de l’incertitude à l’ancienne donne : \[\Delta x=\frac{1}{n}n\Delta {{x}_{1}}+\frac{1}{n}\Delta e=\Delta {{x}_{1}}+\frac{1}{n}\Delta e\]
L’incertitude de lecture apparaît bien divisée par n mais l’intérêt de faire une moyenne n’apparaît pas sur l’incertitude de visée.
Le résultat d’une mesure vue comme variable aléatoire
Le point de vue moderne est de considérer que le mesurage d’une grandeur est modélisé par une variable aléatoire dont on peut alors quantifier la dispersion.
Une variable aléatoire réelle est une application de l’ensemble des éventualités dans l’ensemble des réels.
Dans le cas du mesurage, on peut supposer que les éventualités sont toutes les opérations de mesures possibles d’une même grandeur et la valeur de la variable aléatoire est le résultat du mesurage.
La loi de la variable aléatoire permet de calculer la probabilité qu’un résultat de mesurage donné se réalise. A priori n’importe quelle valeur positive est un résultat possible et donc les variables utilisées sont à densité.
On en verra des exemples classiques au paragraphe 4.2.
Une hypothèse raisonnable est que cette variable aléatoire a une espérance égale à la vraie valeur inconnue de la grandeur compte tenu de la correction de l’erreur systématique éventuelle.
Écart-type
L’écart-type permet de quantifier la dispersion de la variable aléatoire autour de son espérance : \[{{\sigma }_{X}}=\sqrt{ {\rm E} ((X- {\rm E} (X)){}^\text{2})}\] En physique on l’appelle l’incertitude-type.
Une propriété importante est la formule concernant l’écart-type de la somme de deux variables indépendantes : \[{{\sigma }_{x+y}}=\sqrt{\sigma _{X}^{2}+\sigma _{Y}^{2}}\] On a aussi : \[{{\sigma }_{aX}}=\left| a \right|{{\sigma }_{X}}\]
Appliquons cela dans le cas du cercle de Borda. On suppose les mesures aléatoires \[{{X}_{1}},...,{{X}_{n}}\] obtenues par visées de l’angle indépendantes de même écart-type et indépendantes de l’erreur de lecture finale E.
On a :
\[\sigma _{X}^{2}=\frac{1}{n^2}n\sigma^2+\frac{1}{n^2}\sigma _{E}^{2}=\frac{1}{n}\sigma ^2+\frac{1}{n^2}\sigma _{E}^{2}L\]
La composante issue des n visées
\[\frac{1}{n}\sum\limits_{k=1}^{n}{{{X}_{k}}}\]
a un écart-type divisé par \[\sqrt{n}\] par rapport à une seule visée.
Probabilités associées à l’écart-type
Pour calculer la probabilité que la variable $X$ s’écarte de son espérance de plus de un ou deux ou trois écarts-type, il est nécessaire de connaître la loi de $X$.
Sans information précise, on a les résultats suivants conséquences de l’inégalité de Bienaymé-Tchebychev :
\[ {\rm P} \left( \left| X- {\rm E} (X) \right|\ge a \right)\le \frac{\sigma {}^\text{2}}{a{}^\text{2}},\]
\[ {\rm P} \left( \left| X- {\rm E} (X) \right|\ge 2\sigma \right)\le 0,25\]
et
\[ {\rm P} \left( \left| X- {\rm E} (X) \right|\ge 3\sigma \right)\le 0,12\]
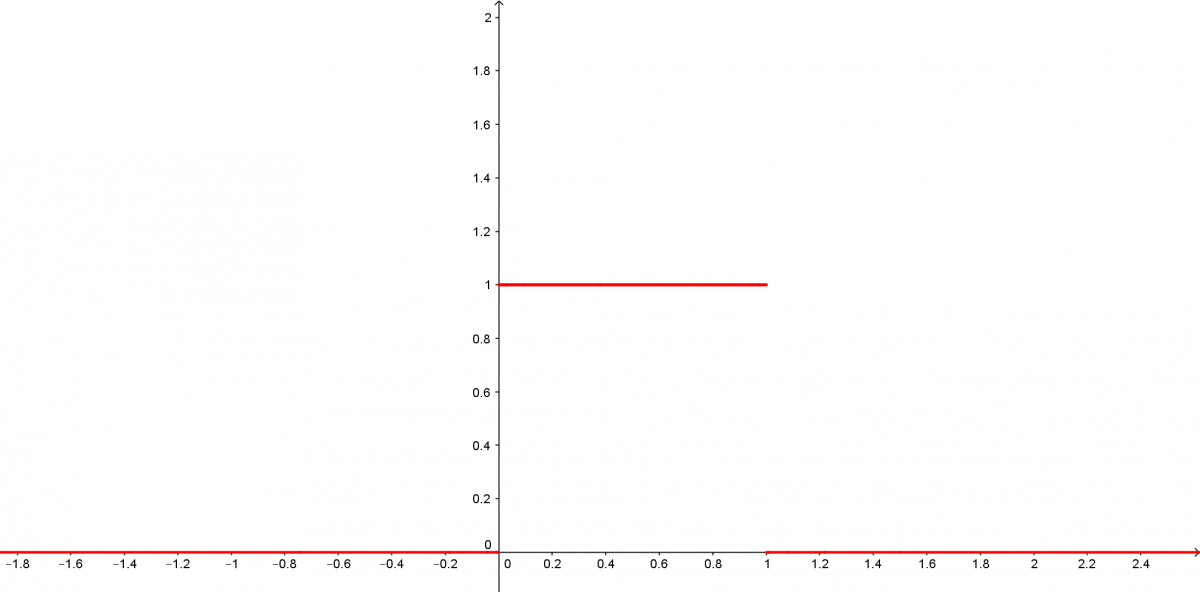
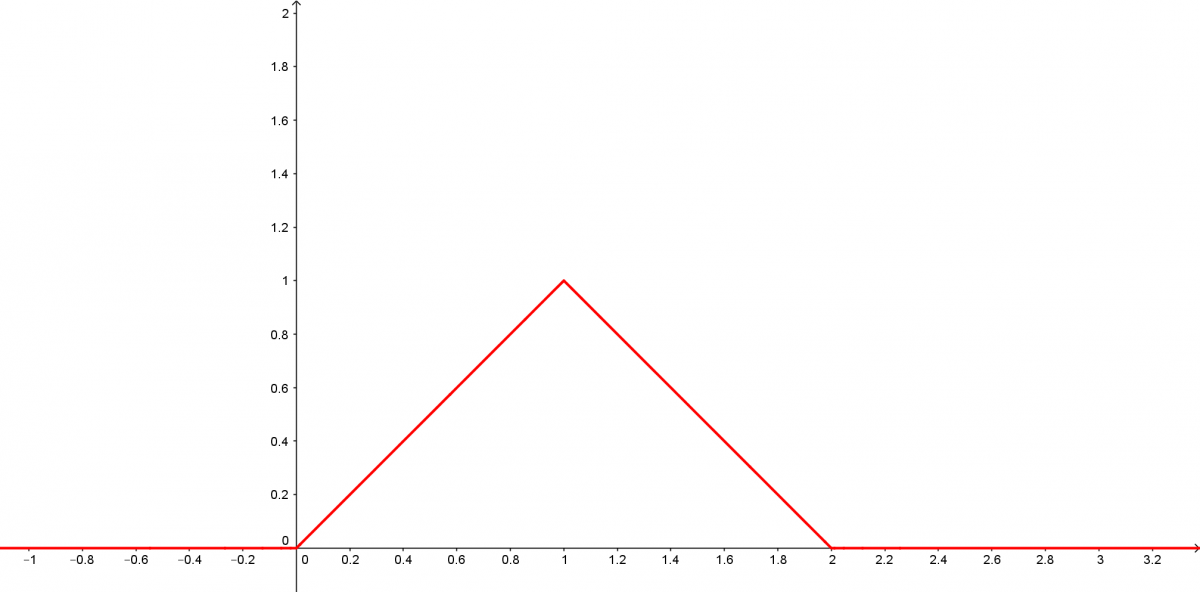
Les lois les plus utilisées dans les mesurages sont les lois uniformes, triangulaires et normales.
Voici l’allure du graphe de leurs densités.
Voici les résultats obtenus avec ces trois lois :
Voici les résultats obtenus avec ces trois lois La loi triangulaire est la loi de la somme de deux variables uniformes indépendantes et de même loi. Elle apparaît notamment lors d’un double mesurage.
Les calculs donnant ces résultats peuvent faire l’objet d’exercices en terminale en utilisant la formule \[\text{V}(X)=\int_{I}{t{}^\text{2}f(t)\text{d}t}-\left( {\rm E} (X) \right){}^\text{2}\]
Pour la loi uniforme on utilise sa densité et pour la loi triangulaire on peut utiliser la représentation graphique de la densité et des calculs d’aires de triangles.
Il faut noter que pour la plupart des lois usuelles \[ {\rm P} \left( -2\sigma \le X- {\rm E} (X)\le 2\sigma \right)\] est supérieur à 0,9.
Incertitudes composées
Il est fréquent qu’une grandeur soit fonction de plusieurs grandeurs que l’on peut mesurer :
\[G=f({{X}_{1}},...,{{X}_{n}})\]
On suppose que l’on connaît les écarts-type des variables \[{{X}_{1}},...,{{X}_{n}}\] et que f possède des dérivées partielles d’ordre 1.
On peut alors « linéariser » l’expression de f au voisinage du point \[( {\rm E} ({{X}_{1}}),...., {\rm E} ({{X}_{n}}))\] à l’aide d’un développement limité.
Voici l’expression pour le cas de deux variables :
\[f(X,Y)=f( {\rm E} (X), {\rm E} (Y))+\frac{\partial {{f}_{{}}}}{\partial x}( {\rm E} (X), {\rm E} (Y))\left( X- {\rm E} (X) \right)+\\ \frac{\partial {{f}_{{}}}}{\partial y}( {\rm E} (X), {\rm E} (Y))\left( Y- {\rm E} (Y) \right)+reste.\]
On suppose le reste négligeable et les variables indépendantes.
L’espérance de \[f(X,Y)\] vaut environ \[f( {\rm E} (X), {\rm E} (Y))\]
La variance de \[f(X,Y)\] vaut environ, grâce à l’indépendance,
\[\sigma _{X}^{2}(\frac{\partial f}{\partial x}( {\rm E} (X), {\rm E} (Y))){}^\text{2}+\sigma _{Y}^{2}(\frac{\partial f}{\partial y}( {\rm E} (X), {\rm E} (Y))){}^\text{2}\]
Exemple :
La période $t$ d’un pendule pesant simple de longueur $l$ dans le cas de petites oscillations est donnée par la formule \[t=2\pi \sqrt{\frac{l}{g}},\] et on a donc $g = 4π^2l/t^2.$
On en déduit une méthode permettant d’estimer la valeur de l’accélération de la pesanteur $g.$
On suppose que $l$ et $t$ sont mesurées et que le résultat de leurs mesurages sont deux variables aléatoires indépendantes $L$ et $T.$
Un estimateur de $g$ est alors la variable aléatoire \[G=4\pi {}^\text{2}\frac{L}{T{}^\text{2}}=f(L,T)\]
On suppose que le mesurage de l se fait avec une précision de 1mm et que toutes les valeurs de part et d’autre de la valeur observée sont équiprobables ce qui conduit à supposer que \[L-l\]suit une loi uniforme sur $\left[ -0,001;0,001 \right].$
On suppose que le mesurage de $t$ se fait par deux lectures du chronomètre, au début des oscillations et à la fin.
Pour diminuer l’incertitude on mesure 50 oscillations successives. Chacune de ces lectures est précise à 1/10 seconde près et comme pour $l$ toutes les valeurs autour de la valeur observée sont équiprobables.
Donc $T-t$ est la somme de deux lois uniformes indépendantes sur $\left[ -0,002;0,002 \right]$ ce qui fait que $T-t$ suit une loi triangulaire sur $\left[ -0,004;0,004 \right].$
Avec ces hypothèses, on peut vérifier que G est légèrement biaisé (c'est-à-dire que $ {\rm E} (G)\ne g$) mais l’approximation linéaire vue plus haut donne :
\[ {\rm E} (G)\approx f( {\rm E} (L), {\rm E} (T))=f(l,t)=g\]
Calculons une valeur approchée de la variance de G : \[\sigma _{G}^{2}\approx \sigma _{L}^{2}(\frac{\partial f}{\partial x}(l,t)){}^\text{2}+\sigma _{T}^{2}(\frac{\partial f}{\partial y}(l,t)){}^\text{2}\]
On a : \[\frac{\partial f}{\partial x}(l,t)=\frac{4\pi {}^\text{2}}{t{}^\text{2}}\] et \[\frac{\partial f}{\partial y}(l,t)=4\pi {}^\text{2}l\left( \frac{-2}{{{t}^{3}}} \right)\]
Supposons que l’on a un pendule de 1m et que la période mesurée soit de 2 secondes.
Avec les hypothèses faites on a : \[\sigma _{L}^{2}=\frac{(2\times 0,001){}^\text{2}}{12}\] et \[\sigma _{T}^{2}=\frac{0,004{}^\text{2}}{6}\]
Cela donne : \[\sigma _{G}^{2}\approx {{\pi }^{4}}{{10}^{-6}}\left( \frac{4}{12}+\frac{16}{6} \right)\] soit \[{{\sigma }_{G}}\approx \sqrt{3}\pi {}^\text{2}{{10}^{-3}}\approx 0,017\]
La loi de $G$ est difficile à obtenir exactement mais on peut en avoir une bonne estimation par simulation avec le logiciel Scilab.
On obtient en faisant 10000 itérations des estimations de l’espérance de G et de son écart-type. On peut alors en refaisant une nouvelle série de 10000 itérations obtenir une estimation de la probabilité que $G$ s’écarte de plus de deux écarts-type de son espérance.
On a obtenu par exemple pour ces trois quantités respectivement : 9,807 ; 0,0167 ; 0,035.
Voici ci-dessous un histogramme des valeurs de G obtenues qui donne un bon aperçu de la densité de G :
Nous verrons plus loin pourquoi on obtient une belle courbe en cloche.
La loi des erreurs de Gauss
Dans son ouvrage « Theoria motus corporum celestium » publié en 1809 Gauss introduit la loi normale par le principe du maximum de vraisemblance. (Chabert 1989, p. 13 )
Rappelons en quoi consiste ce principe. On suppose que l’on cherche un estimateur d’une quantité inconnue a, c’est à dire une variable aléatoire dépendant de a dont on espère que les réalisations fourniront de bonnes estimations de a.
On suppose que l’on a une réalisation ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ d’un n-échantillon ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$ de variables indépendantes de même loi dépendant du paramètre a que l’on veut estimer.
Dans le cas discret ${{X}_{1}}={{x}_{1}},{{X}_{2}}={{x}_{2}},...,{{X}_{n}}={{x}_{n}}$ avait une probabilité $ {\rm P} ({{X}_{1}}={{x}_{1}})\times ...\times {\rm P} ({{X}_{n}}={{x}_{n}})$de se réaliser.
On fait alors le raisonnement suivant : la vraie valeur de a étant inaccessible, on va chercher la plus vraisemblable possible ; c’est-à-dire, compte tenu de l’observation faite, celle qui rendrait la probabilité de cette observation maximale.
Cette valeur dépend de ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ et constitue une estimation de a.
Pour avoir un estimateur, on remplace ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ par ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$ dans l’expression obtenue. En pratique, on remplace a par une variable $A$ et on pose $f(x)= {\rm P} ({{X}_{1}}={{x}_{1}})\times ...\times {\rm P} ({{X}_{n}}={{x}_{n}}).$ On cherche alors la ou les valeurs de $A$ en fonction de ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ qui rendent maximale cette fonction.
Dans le cas continu, si les variables ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$ ont pour densité f, la probabilité précédente est nulle.
On considère alors que la probabilité de s’écarter de $d{{x}_{1}},d{{x}_{2}},...,d{{x}_{n}}$des valeurs ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ est à peu près égale à $f({{x}_{1}})d{{x}_{1}}\times ...\times f({{x}_{n}})d{{x}_{n}}$ et on cherche alors à rendre $f({{x}_{1}})....f({{x}_{n}})$ maximal.
Si on cherche à mesurer une grandeur $a$, le résultat d’une mesure est une variable aléatoire $X$ et l’erreur est donc $X-a.$
On suppose que l’erreur commise lors d’un mesurage suit une loi de densité $f$ telle que le maximum de vraisemblance soit atteint pour la moyenne des observations.
On cherche alors l’expression que doit avoir $f.$
Pour tous \[{{x}_{1}},...,{{x}_{n}}\] observés la fonction \[g(x)=f({{x}_{1}}-x)\times ...\times f({{x}_{n}}-x)\] doit donc être maximale pour la moyenne m des observations ce qui entraîne que \[g'(m)=0\]
En remarquant que la fonction de densité est positive, $g$ est maximale si et seulement si $\ln(g)$ est maximale. Comme \[\ln (g(x))=\sum\limits_{k=1}^{n}{\ln }f({{x}_{k}}-x)\] on obtient une condition nécessaire pour $f$ : \[\sum\limits_{k=1}^{n}{\frac{f'({{x}_{k}}-m)}{f({{x}_{k}}-m)}=0}\]
En posant \[h(x)=\frac{f'(x)}{f(x)}\] on obtient \[\sum\limits_{k=1}^{n}{h({{x}_{k}}-m)=0}.\]
1) Prenons $n=2$
On obtient \[h\left( {{x}_{1}}-\frac{{{x}_{1}}+{{x}_{2}}}{2} \right)+h\left( {{x}_{2}}-\frac{{{x}_{1}}+{{x}_{2}}}{2} \right)=0\]
Pour tous ${{x}_{1}},{{x}_{2}}$ on a donc
\[h\left( \frac{{{x}_{1}}-{{x}_{2}}}{2} \right)=-h\left( \frac{{{x}_{2}}-{{x}_{1}}}{2} \right)\]
$h$ est donc nécessairement impaire.
2) Prenons $n=3$
Pour tous ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ on a \[h\left( \frac{2{{x}_{1}}-{{x}_{2}}-{{x}_{3}}}{3} \right)+h\left( \frac{2{{x}_{2}}-{{x}_{1}}-{{x}_{3}}}{3} \right)+h\left( \frac{2{{x}_{3}}-{{x}_{1}}-{{x}_{2}}}{3} \right)=0\]
En posant \[u=\frac{2{{x}_{1}}-{{x}_{2}}-{{x}_{3}}}{3}\] et \[v=\frac{2{{x}_{2}}-{{x}_{1}}-{{x}_{3}}}{3}\] on obtient que pour tous $u$ et $v$
\[h(u)+h(v)=-h(-u-v)=h(u+v)\] par imparité.
Un résultat usuel d’analyse est que les seules fonctions continues vérifiant la linéarité pour la somme sont les fonctions linéaires. $h$ est donc nécessairement linéaire.
3) On pose donc $h(x)=\alpha x$
On en déduit \[\ln (f(x))=\frac{1}{2}\alpha x{}^\text{2}+b\] puis \[f(x)={{e}^{b}}{{e}^{\frac{1}{2}\alpha {{x}^{2}}}}\]
4) $f$ étant une densité on doit avoir $\alpha
\[\int_{-\infty }^{+\infty }{f(x)\text{d}x}\]
et
\[b=\sqrt{-\frac{\alpha }{2\pi }}\]
pour que celle-ci soit égale à 1.
5) Réciproquement, la densité trouvée conduit bien à un maximum de vraisemblance obtenu pour la moyenne.
Conclusion :
La seule loi des erreurs pour laquelle le maximum de vraisemblance est obtenu pour la moyenne est la loi normale centrée.
La méthode de la moyenne pour réduire l’incertitude
On a vu apparaître au paragraphe 6 un estimateur très utilisé : la moyenne arithmétique d’un n-échantillon ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$.
Cet estimateur peut également être obtenu par la méthode des moindres carrés. On cherche à estimer une grandeur par n mesures (comme dans le cercle de Borda).
On suppose que l’on a obtenu une réalisation de ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$ notée ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ et on cherche une valeur x rendant minimale la somme $\sum\limits_{k=1}^{n}{\left( {{x}_{k}}-x \right)}{}^\text{2}$. Un petit calcul de dérivée montre que cette valeur est la moyenne des ${{x}_{k}}$.
On retrouve l’estimateur ${{T}_{n}}=\frac{1}{n}\sum\limits_{k=1}^{n}{{{X}_{k}}}$ qui est donc parmi toutes les variables aléatoires celle qui minimise sa « distance » avec les variables ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$. Il est facile de voir que $V({{T}_{n}})=\frac{1}{n}V({{X}_{1}})$ (grâce à l’indépendance) et donc que l’estimateur ${{T}_{n}}$ est n fois plus « efficace » que ${{X}_{1}}.$
Le calcul des incertitudes en physique-chimie
On peut maintenant détailler les méthodes mises en œuvre pour quantifier l’incertitude sur un mesurage. Ces méthodes sont de type A et B.
Les méthodes de type A permettent de quantifier l’incertitude qui apparaît lorsque l’on fait plusieurs mesurages de la même grandeur (incertitude de répétabilité).
Les méthodes de type B permettent de quantifier les autres sources d’erreur provenant du processus de mesurage lui-même. On cherche à évaluer l’incertitude-type pour un seul mesurage en modélisant avec une loi de probabilité a priori.
Incertitudes de type A
Les métrologues qualifient le calcul d’incertitude de type A de méthode statistique.
On ne tient pas compte ici des erreurs dues aux appareils de mesure (ce sont celles de type B vues au paragraphe 8.2) mais seulement de celles dues à l’opérateur.
On suppose que l’on effectue n mesurages de la même grandeur inconnue a modélisés par un n-échantillon ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$ de n variables aléatoires indépendantes et de même loi inconnue.
Il est raisonnable de supposer que ces variables ont la même espérance $a.$
Il s’agit alors de déduire de l’échantillon une estimation de a et de l’écart-type $\sigma$ commun aux n variables. Il est clair que ${{T}_{n}}=\frac{1}{n}\sum\limits_{k=1}^{n}{{{X}_{k}}}$a pour espérance $a$.
C’est cette variable que l’on choisit comme estimateur de $a$.
Il faut maintenant trouver un estimateur de $\sigma$.
Si on a une réalisation${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$, la variance de cette série de valeurs est $\frac{1}{n}\sum\limits_{k=1}^{n}{({{x}_{k}}-\bar{x})}{}^\text{2}$.
Il est donc naturel de prendre comme estimateur de $\sigma^2 $ la variable${{Y}_{n}}=\frac{1}{n}\sum\limits_{k=1}^{n}{({{X}_{k}}-T_{n}^{{}})}{}^\text{2}.$
Calculons son espérance en utilisant la linéarité.
$$ {\rm E} ({{Y}_{n}})=\frac{1}{n} {\rm E} \left( \sum\limits_{k=1}^{n}{{{({{X}_{k}}-T_{n}^{{}})}^{2}}} \right)=\frac{1}{n}\sum\limits_{k=1}^{n}{ {\rm E} \left( X_{k}^{2}-2{{X}_{k}}T_{n}^{{}}+T_{n}^{2} \right)}$$
$$\begin{align} {\rm E} ({{Y}_{n}}) & =\frac{1}{n}\left( \sum\limits_{k=1}^{n}{ {\rm E} (X_{k}^{2})-2 {\rm E} ({{X}_{k}}{{T}_{n}})+ {\rm E} (T_{n}^{2})} \right) = a^2+\sigma ^2-2 {\rm E} (T_{n}\frac{1}{n}\sum\limits_{k=1}^{n}{{{X}_{k}}})+ {\rm E} (T_{n}^2) \\ & =a^2+\sigma^2- {\rm E} (T_{n}^2)=a^2+\sigma^2-V({{T}_{n}})- {\rm E} ({{T}_{n}})^2 \\ & =a^2+\sigma^2-\frac{1}{n}\sigma^2-a^2=\frac{n-1}{n}\sigma^2 \end{align}$$
L’estimateur a donc un biais et on le corrige en prenant comme estimateur de $\sigma^2$ la variable $Y_{n}^{'}=\frac{n}{n-1}Y_{n}^{{}}$ dont l’espérance est $\sigma^2$.
On obtient donc une estimation de $\sigma$ par l’écart-type expérimental ${{u}_{r}}=\sqrt{\frac{1}{n-1}\sum\limits_{k=1}^{n}{({{x}_{k}}-\bar{x})}{}^\text{2}}$ appelé aussi incertitude-type de répétabilité.
Il faut noter que si $n$ est grand la différence entre les deux variables ${{Y}_{n}}$ et $Y_{n}^{'}$ est négligeable.
Maintenant que nous avons des estimateurs ponctuels de $a$ et de $\sigma^2$, on peut trouver une estimation de $a$ par un intervalle de confiance.
Le théorème central limite permet de dire que la suite de variables centrées réduites \[T_{n}^{*}=\frac{{{T}_{n}}-a}{\sigma ({{T}_{n}})}\]converge en loi vers une variable normale centrée et réduite $Z$.
Pour $n$ assez grand on peut utiliser l’approximation \[ {\rm P} \left( -2\le T_{n}^{*}\le 2 \right)\approx {\rm P} \left( -2\le Z\le 2 \right)\approx 0,95\] ce qui conduit à \[ {\rm P} \left( {{T}_{n}}-2\sigma ({{T}_{n}})\le a\le {{T}_{n}}+2\sigma ({{T}_{n}}) \right)\approx 0,95\]
On a \[\sigma \left( {{T}_{n}} \right)=\frac{1}{\sqrt{n}}\sigma \approx \frac{1}{\sqrt{n}}{{u}_{r}}\]
On en déduit un intervalle de confiance numérique de a à 95% :
\[\left[ \bar{x}-2\frac{u_{r}^{{}}}{\sqrt{n}},\bar{x}+2\frac{{{u}_{r}}}{\sqrt{n}} \right]\]
Dans la pratique, l’incertitude type de répétabilité ${{u}_{r}}$ a pu être obtenue par $n$ mesurages effectués auparavant et même parfois dans un autre laboratoire.
Elle peut alors être utilisée pour une série de $p$ nouveaux mesurages ayant donné les résultats ${{x}_{1}},{{x}_{2}},...,{{x}_{p}}$et on obtient alors l’intervalle de confiance à 95% \[\left[ \bar{x}-2\frac{u_{r}^{{}}}{\sqrt{p}},\bar{x}+2\frac{{{u}_{r}}}{\sqrt{p}} \right]\]
Si $n$ n’est pas assez grand pour utiliser une approximation normale et si on peut faire l’hypothèse que les variables ${{X}_{1}},{{X}_{2}},...,{{X}_{n}}$ suivent approximativement des lois normales (ce qui est assez fréquent), le coefficient 2 est remplacé par un coefficient plus grand issu de la loi de Student. Par exemple pour $n=5$ on prend 2,78.
Incertitudes de type B
On choisit une loi rectangulaire (ou uniforme) quand la vraie valeur peut se situer uniformément entre deux valeurs lues, typiquement avec un instrument à aiguille.
On choisit une loi triangulaire lorsque l’on a de bonnes raisons de penser que la vraie valeur a plus de chance de se trouver près de la valeur lue qu’aux extrêmes.
Cette loi peut aussi être donnée par le fabriquant de l’appareil de mesure (par exemple pour la pipette jaugée ci-dessous).
La loi triangulaire apparaît également quand la grandeur est obtenue par un double mesurage : l’erreur est alors la somme de deux lois uniformes indépendantes et identiques qui est une loi triangulaire (cas d’un mesurage de longueur avec une règle graduée).
Incertitudes composées
Comme vu au paragraphe 5, la grandeur $g$ que l’on veut estimer est souvent une fonction de plusieurs grandeurs dont on doit effectuer le mesurage et il est possible que l’on fasse plusieurs mesurages de certaines de ces grandeurs.
L’incertitude sur $g$ est donc composée de plusieurs incertitudes : celles de type A provenant éventuellement d’une estimation de certaines grandeurs par la moyenne obtenue lors de plusieurs mesurages et celles de type B provenant des instruments de mesures. Il en résulte que l’on peut modéliser le processus de mesurage par une expression du type :
\[G=f({{X}_{1}},...,{{X}_{n}})\]
On a vu que sous certaines conditions d’approximation on pouvait linéariser cette expression grâce à un développement limité à l’ordre 1 sous la forme :
\[G\approx {\rm E} (G)+\sum\limits_{k=1}^{n}{{{c}_{k}}({{X}_{k}}- {\rm E} ({{X}_{k}})})\]
L’écart-type de $G$ vaut approximativement (en supposant l’indépendance des variables) :
\[\sigma (G)\approx \sqrt{\sum\limits_{k=1}^{n}{c_{k}^{2}\sigma {}^\text{2}({{X}_{k}})}}\] qui est donc l’incertitude-type composée que l’on note ${{u}_{c}}(G).$
Incertitude élargie
Une version généralisée du théorème central limite permet d’affirmer que si aucune des variables ${{X}_{k}}$ n’est prépondérante alors $G$ suit approximativement une loi normale même dans le cas de lois différentes.
On en a vu une illustration avec le pendule pesant : les 3 variables intervenant dans $G$ sont rectangulaires et on obtient un histogramme très proche d’une loi normale.
On peut alors considérer que \[\frac{G- {\rm E} (G)}{\sigma (G)}\] suit approximativement une loi normale centrée et réduite. Comme vu précédemment on suppose raisonnablement que $ {\rm E} (G)=a$ où $a$ est la grandeur inconnue que l’on veut estimer.
On obtient alors \[ {\rm P} \left( -2\le \frac{G-a}{\sigma (G)}\le 2 \right)\approx 0,95\] d’où l’on déduit un intervalle de confiance de $a$ :
\[\left[ G-2\sigma (G),G+2\sigma (G) \right]\]dont la probabilité de contenir a est environ 0,95.
On peut alors conclure le mesurage en donnant un intervalle de confiance numérique de a à 95% en remplaçant G par le résultat du mesurage et $\sigma (G)$ par ${{u}_{c}}(G).$
Dans le cas du pendule cela donne $g=9,81\pm 0,034\quad $ au seuil de 95%.
Les métrologues parlent alors d’incertitude élargie. Il faut noter que l’on procède à l’élargissement en fin de processus et non sur les différentes composantes.
Le coefficient 2 d’élargissement suppose une approximation normale et est très souvent utilisé mais il se peut que dans certains cas particuliers il ne soit pas adapté par exemple dans le cas de mesurages répétés en petit nombre (où il est trop petit) ou d’une grandeur obtenue par une seule mesure dont l’erreur est supposée rectangulaire (où il est trop grand).
Bibliographie
Bureau International des Poids et Mesures. Guide pour l’expression de l’incertitude de mesure. www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_F.pdf
Chabert, J.-L. Gauss et la méthode des moindres carrés. Revue d’Histoire des Sciences XLII 1/2 (1989), pp. 5-26. http://www.persee.fr/issue/rhs_0151-4105_1989_num_42_1?sectionId=rhs_0151-4105_1989_num_42_1_4132
Guedj, D. Le mètre du monde. Ed. du Seuil 2000.
Ministère de l’Education nationale. Document ressource (Eduscol)
Parzysz, B. (2013) La longue genèse de la loi normale. Bulletin de l’APMEP 502, pp. 29-40
Trystram, F. Le procès des étoiles. Récit de la prestigieuse expédition de trois savants français en Amérique du sSud, 1735-1771. Ed. Payot 2001.