On a tous un jour réduit la taille d'un fichier comportant une photo en diminuant la résolution, et on comprend bien comment cela marche (on enlève des pixels), et qu'on ne pourra pas revenir exactement en arrière. Mais on a aussi tous utilisé des utilitaires de compression/décompression de fichiers ou d'archives comme gzip ou winzip. On sait qu'on récupère alors exactement le même fichier que le fichier initial. On va voir ici les principes qui sont à la base de la plupart de ces algorithmes de compression sans perte.
Des algorithmes utiles
On a tous un jour réduit la taille d'un fichier comportant une photo en diminuant la résolution, et on comprend bien comment cela marche (on enlève des pixels), et qu'on ne pourra pas revenir exactement en arrière. On parle alors de compression avec perte. Mais on a aussi tous utilisé des utilitaires de compression/décompression de fichiers ou d'archives comme gzip ou winzip. On sait qu'on récupère alors exactement le même fichier que le fichier initial. On va voir ici les principes qui sont à la base de la plupart de ces algorithmes de compression sans perte.
Le codage binaire
Un petit rappel tout d'abord sur la manière dont un fichier est stocké dans un ordinateur : celui-ci ne connaît que les 0 et les 1 (qui correspondent à « pas de courant » ou « du courant », appelés des bits. Donc pour un fichier comportant du texte, on doit trouver un moyen de transformer (coder) tout l'alphabet avec des 0 et des 1 : on cherche un code 1 binaire.
Comment ferait-on par exemple avec un alphabet de quatre lettres $A,B,C,D$ ?
On pourrait coder comme ceci :
$\begin{eqnarray*}
A&\rightarrow &00\\
B&\rightarrow &01\\
C&\rightarrow &10\\
D&\rightarrow &11
\end{eqnarray*}$
(Cela revient à numéroter l'alphabet en partant de $0$, et à écrire les nombres correspondant en base 2). $00$, $01$, $10$, $11$ sont appelés les mots du code, même s'ils ne codent qu'une lettre.
Pour décoder : on décompose en morceaux de deux bits, et on décode morceau par morceau. Ici, par exemple, $11001100$ correspond à $DADA$.
On voit ainsi que des suites de $0$ et de $1$ de longueur $n$ permettent de coder $2^n$ lettres différentes. Pour un alphabet de 26 lettres on devrait donc utiliser des mots de longueur 5. Pour un alphabet de $n$ lettres, la longueur des mots nécessaire est le plus petit exposant $l$ tel que $2^l \geq n$.
Remarque : il s'agit de $l=\lceil \log_2 n \rceil$, en notant $\lceil x \rceil$ l'entier supérieur le plus proche de $x$. Rappelons que $\log_2(x) = \ln(x)/\ln(2)$ vérifie en particulier $\log_2(2^k) = k$.
En fait, un code très utilisé par les ordinateurs comme le code ASCII étendu utilise des suites de 8 bits (appelées octets). Il permet donc de coder théoriquement 256 caractères (lettres minuscules, majuscules, ponctuation, chiffres, symboles divers...). Une partie de ce code est :
\[\begin{array}{||c|c||c|c||c|c||c|c||}
\hline
A\mathstrut&01000001&I&01001001&Q&01010001&Y&01011001\\
B&01000010&J&01001010&R&01010010&Z&01011010\\
C&01000011&K&01001011&S&01010011& &00100000\\
D&01000100&L&01001100&T&01010100&.&00101110\\
E&01000101&M&01001101&U&01010101&,&00101100\\
F&01000110&N&01001110&V&01010110&?&00111111\\
G&01000111&O&01001111&W&01010111&!&00100001\\
H&01001000&P&01010000&X&01011000&:&00111010\\
\hline
\end{array}
\]
On peut par exemple décoder le message suivant (pour faciliter la tâche au lecteur, on a mis en couleur un octet sur 2; on rappelle qu'il n'y a pas d'espace pour l'ordinateur) :
01010011010000010100110001010101010101000010000000100001
SALUT!
Différents codes binaires similaires sont utilisés pour encoder les fichiers (isolatin, utf8, etc...) ; ils sont décrits par des normes internationales. Lorsqu'on reçoit des mails où les accents (ou les apostrophes) ressortent bizarrement, c'est souvent qu'on n'utilise pas le bon code.
Codes de longueurs variables
Si on utilise le code ASCII précédent, un fichier pour un texte comportant $n$ lettres comportera $8n$ bits. Le but de la compression est de trouver un moyen pour que les fichiers codés soient plus courts que cela (pour que les fichiers stockés dans l'ordinateur prennent moins de place). On va donc devoir changer de code.
Principe de la compression sans perte de données
L'idée essentielle est de ne pas coder toutes les lettres avec le même nombre de bits : on veut profiter de ce que le $E$ par exemple est beaucoup plus fréquent (en français) que le $K$, comme tout joueur de Scrabble le sait bien. Donc si le $E$ pouvait être codé sur moins de 8 bits, quitte à ce que le $K$ soit plus long, on pourrait y gagner.
Mais le problème est qu'on veut toujours pouvoir déchiffrer. Or on rappelle qu'on ne peut pas mettre d'espace entre deux mots du code (car l'ordinateur ne connaît pas les espaces, il ne connaît que 0 et 1).
Un code non déchiffrable
Par exemple, si on décide de coder un alphabet de quatre lettres comme ceci :
\begin{eqnarray*}
A&\rightarrow &0\\
B&\rightarrow &01\\
C&\rightarrow &10\\
D&\rightarrow &11
\end{eqnarray*}
Comment décoder $0010$ ?
AAC ou ABA ?
Il y a ambiguïté, et ce code est donc un mauvais code.
Codes préfixes
Pour éviter ce problème, on fait en sorte d'utiliser des suites de 0 et de 1 telles qu'aucune ne soit le début d'une autre. On dit que le code est préfixe. Dans le code précédent, $0$ (A) était le début de $01$ (B), et c'est pour cela qu'on pouvait avoir ambiguïté. 1
Si on prend par exemple :
\begin{eqnarray*}
A&\rightarrow &0\\
B&\rightarrow &10\\
C&\rightarrow &110\\
D&\rightarrow &111
\end{eqnarray*}
$0$ n'est pas le début de 10, ni de 110, ni de 111. De même, 10 n'est le début ni de 110 ni de 111. Donc quand on cherche à décoder un message, on peut lire de gauche à droite, et dès qu'on reconnaît un mot du code, c'est forcément lui (et pas le début d'un autre).
Exemple :
Décodez $1110110$ puis $100110$ 2
Question : le code ci-dessous est-il préfixe ?
$$
\begin{array}{lcl}
A&\rightarrow &01\\
B&\rightarrow &101\\
C&\rightarrow &110\\
D&\rightarrow &111
\end{array}
\begin{array}{lcl}
E&\rightarrow &001\\
F&\rightarrow &000\\
G&\rightarrow &{0100}\\
H&\rightarrow &100
\end{array}$$
Non : A est le début de G
Les codes poussent sur les arbres
On a vu qu'un code préfixe permet d'avoir des mots de code de longueur variable. Mais comment vérifier qu'un code est préfixe, ou en construire un facilement ?
Une manière très pratique pour cela est de « mettre le code sur un arbre ».
Arbre binaire enraciné
Pour construire un arbre binaire, on commence, comme dans un arbre généalogique, par une racine ($\bullet$) que l'on mettra en haut, qui est le premier nœud; chaque nœud a ensuite 0 ou deux enfants qui sont de nouveaux nœuds.
Un nœud qui n'a pas d'enfant est une feuille (on mélangera allègrement le vocabulaire lié à la botanique et à la généalogie).
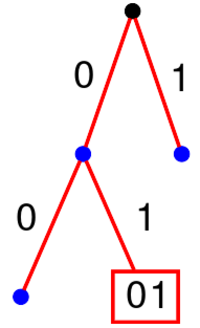
Pour mettre les mots d'un code sur un arbre, on associe à chacune des deux branches qui joignent un nœud à ses enfants un bit différent (0 pour la branche gauche, 1 pour la branche droite). On place ensuite les mots du code sur les nœuds de l'arbre, en suivant le chemin qui correspond au mot depuis la racine. On rajoute des nœuds et des branches si nécessaire.
Exemples avec les codes précédents
Le code montré ci-contre est mauvais, car ce n'est pas un code préfixe.
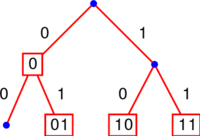
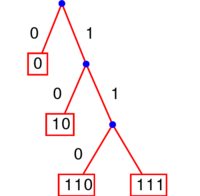
Le code montré ci-contre est bien un code préfixe.
Le fait d'être préfixe se voit facilement sur l'arbre : en effet, « être le début de » signifie être plus haut sur le même chemin, donc cela signifie être un ascendant. Dit autrement, un code est préfixe si et seulement si tous les mots du code sont sur des feuilles de l'arbre. Ou encore, une fois qu'on a choisi un mot du code, on ne peut plus choisir aucun de ses descendants.
Le lecteur est vivement encouragé à essayer de construire plusieurs codes préfixes permettant de coder 5 lettres A, B, C, D, et R.
Quel code choisir ?
On peut avoir plusieurs codes préfixes pour un alphabet. Suivant les fréquences des lettres dans le texte à coder , un code pourra être plus efficace qu'un autre. On se doute bien que les lettres les plus fréquentes doivent être codées par un mot plus court. Mais c'est plus compliqué que cela.
Par exemple, si on a un texte de 100 lettres avec 50 A, 30 B, 10 C et 10 D : si on utilise le code
$\begin{array}{ccc}
A&\rightarrow &0\\
B&\rightarrow &10\\
C&\rightarrow &110\\
D&\rightarrow &111
\end{array}
$
on obtient un texte codé de longueur $50+30\times 2+10\times 3+10\times 3 = 170$ bits.
Si on avait utilisé le code
$\begin{array}{ccc}
A&\rightarrow &00\\
B&\rightarrow &01\\
C&\rightarrow &10\\
D&\rightarrow &11
\end{array}
$
le texte codé aurait eu une longueur de 200 bits : on a donc ici intérêt à utiliser le premier code. Mais si on a un texte de 100 lettres avec 28 A, 25 B, 24 C et 23 D, le premier code fournit un texte codé de longueur 219 bits. Le deuxième code aurait fourni un texte codé de longueur toujours 200. Ici c'est donc le deuxième code qui est meilleur !
Il ne suffit donc pas de connaître l'ordre de fréquence des lettres... Le meilleur code dépend donc vraiment des valeurs des fréquences dans le texte qu'on veut compresser.
À la recherche du code optimal
Le problème est donc de trouver un code préfixe qui soit le meilleur possible avec des fréquences données, puisqu'on a vu que suivant les fréquences des lettres, un code sera plus ou moins efficace qu'un autre. David Huffman a publié, en 1952, l'algorithme qui porte son nom et permet, lorsqu'on connaît les fréquences des lettres dans un fichier, de trouver l'arbre qui correspond au code préfixe qui raccourcira le plus le fichier.
Algorithme de Huffman
Cet algorithme est basé sur la remarque suivante.
Dans un code optimal, les deux caractères les moins fréquents seront codés par les mots les plus longs, et en fait par deux mots de même longueur. En effet, sinon, le mot le plus long a son frère inutilisé, on peut donc le remonter d'un cran (en conservant un code préfixe).
On peut de plus aussi s'arranger pour que ces deux mots les plus longs soient deux frères et qu'ils aient donc le même père (s'ils ne le sont pas c'est qu'il y a d'autres mots de la même longueur, mais cela ne change rien de permuter deux mots).
On peut alors identifier les deux lettres codées par ces deux mots, en une lettre fictive codée par le mot père : on obtient un nouveau texte où on a remplacé chaque occurrence de ces deux lettres par ce nouveau caractère; on se retrouve alors à chercher un code optimal pour ce nouveau texte, dont l'alphabet comporte un symbole de moins, et ainsi de suite. C'est une sorte de récurrence descendante : il s'agit d'un principe récursif.
Exemple
Supposons par exemple que l'on veuille coder ABRACADABRA. On commence par établir le nombre d'apparitions de tous les caractères, et par les classer dans l'ordre croissant. Ici on obtient :
$$\begin{array}{|c|c|c|c|c|}
\hline
\mathbf{D}&\mathbf{C}&\mathbf{R}&\mathbf{B}&\mathbf{A}\\
\hline
1&1&2&2&5\\
\hline
\end{array}$$
On prend les deux caractères les moins fréquents : $\mathbf{D}$ et $\mathbf{C}$. Dans un code optimal, d'après la première remarque, ils seront frères, et seront codés par $*0$ pour $\mathbf{D}$ et $*1$ pour $\mathbf{C}$ où $*$ désigne une même suite de 0 et de 1 encore inconnue. On crée alors un nouveau symbole $\mathbf{D \sim C}$ qui remplacera tous les $\mathbf{C}$ et tous les $\mathbf{D}$ (et sera codé par $*$); on est alors amené à chercher un code optimal pour un texte utilisant un alphabet comportant un symbole de moins (4 au lieu de 5), avec les nombres d'apparitions suivants :
$$\begin{array}{|c|c|c|c|}
\hline
\mathbf{D\sim C}&\mathbf{R}&\mathbf{B}&\mathbf{A}\\
\hline
2&2&2&5\\
\hline
\end{array}$$
où $\mathbf{D \sim C}$ sera codé par la suite $*$ précédente. On recommence alors avec les caractères les moins fréquents, qui sont maintenant par exemple $\mathbf{R}$ et $\mathbf{B}$, qui seront aussi frères dans le code qu'on cherche1.
On obtient alors :
$$\begin{array}{|c|c|c|}
\hline
\mathbf{D\sim C}&\mathbf{R\sim B}&\mathbf {A}\\
\hline
2&4&5\\
\hline
\end{array}$$
Enfin, $\mathbf{D \sim C}$ et $\mathbf{R \sim B}$ seront aussi frères, et on obtient
$$\begin{array}{|c|c|}
\hline
\mathbf{(D\sim C)\sim (R\sim B)}&\mathbf{A}\\
\hline
6&5\\
\hline
\end{array}$$
Finalement $\mathbf{A}$ peut être codé par 1, $\mathbf{((D \sim C) \sim (R\sim B))}$ par 0, donc $\mathbf{D \sim C}$ sera codé par 00, $\mathbf{ R\sim B}$ par 01, et enfin $\mathbf{D}$ sera codé par 000, $\mathbf{C}$ par 001, $\mathbf{R}$ par 010, et $\mathbf{B}$ par 011. Ce code est optimal, et fournit une longueur de $5\times 1 + 1\times 3 + 1\times 3 + 2\times 3 + 2\times 3 = 23$ bits pour ABRACADABRA.
Il est à noter qu'il n'y a pas en général unicité du code optimal : de toute évidence, on peut échanger les 0 et les 1, mais on a aussi parfois le choix des deux symboles les moins fréquents : on peut avoir des codes optimaux différents avec des longueurs de mots différentes ! Mais le message codé final aura la même taille. Si à la deuxième étape on avait choisi non pas $\mathbf{R}$ et $\mathbf{B}$ mais par exemple $\mathbf{D \sim C}$ et $\mathbf{R}$ on aurait obtenu un autre code (lequel ?2 ). De plus, pour décoder, on a besoin du code : à la différence des codes comme le code ASCII, régi par des normes, donc connus, ici chaque fichier compressé génère son propre code. Donc le fichier compressé doit aussi contenir le code utilisé (ce qui peut rallonger un peu le fichier...3).
Arbre de Huffman
Dans la pratique on n'écrit pas tous ces tableaux. Si on doit le faire à la main1, on dessine juste un arbre... mais on ne commence pas par la racine.
On commence par écrire tous les symboles par ordre décroissant de fréquence, puis on relie les deux moins fréquents (qui seront deux feuilles de l'arbre) à leur père, à qui on associe comme fréquence la somme des fréquences de ses enfants, et on continue jusqu'à arriver à la racine.
Challenge :
Sauriez-vous coder VIVE LES VACANCES ! (en comptant tous les caractères : en particulier il y a trois espaces et un "!'') ? Quelle sera la longueur de votre message ?
La longueur optimale est de 61 bits.
Efficacité de la compression
La compression telle qu'on l'a décrite profite du fait que certains caractères à coder sont plus fréquents que d'autres. Elle sera donc très efficace pour des fichiers avec du texte en français (ou dans n'importe quelle langue), et moins efficace pour des fichiers comme des exécutables, et pas efficace du tout pour des fichiers où les caractères sont à peu près équidistribués (en particulier il ne sert à rien de chercher à compresser un fichier déjà compressé)1.
L'entropie et les inégalités de Shannon
Claude Shannon, qui est à l'origine de tout ce qu'on présente dans ce texte, a introduit en 1948 (avant donc les travaux de Huffman mentionnés plus haut) une grandeur mathématique pour mesurer à quel point une distribution est loin d'être uniforme, et dont il a montré qu'elle permet de quantifier à quel point la compression peut être efficace. Cette grandeur est appelée l'entropie ; la notion existait déjà depuis le 19ème siècle : elle avait été introduite par Clausius puis Boltzmann en thermodynamique pour mesurer d'une certaine manière le désordre. Claude Shannon n'en était pas conscient, c'est John von Neumann qui a suggéré le nom, après avoir repéré la similitude entre ces notions.
Entropie
On suppose qu'on a un texte comportant $S$ symboles au total, dont $n$ symboles différents, chaque symbole étant présent avec une fréquence $f_i$ (avec $\sum_{i=1}^n f_i = 1$; si le $i$ème symbole est présent $n_i$ fois, on a $f_i = \frac{n_i}{S}$).
L'entropie correspondante, notée $H$1 et mesurée en bits, est $$H = -\sum_{i=1}^n f_i \log_2 f_i$$
Si les fréquences sont toutes identiques égales à $\frac{1}{n}$, $H = \log_2 n$, et on peut montrer que dans le cas général $H \leq \log_2 n$. Plus la distribution a une entropie élevée, plus elle est proche d'une distribution uniforme.
Shannon a entre autres montré en 1948 le théorème suivant, qui dit que l'entropie mesure plus ou moins le nombre moyen de bits par symbole dans le texte codé optimalement.
Inégalités de Shannon
On suppose qu'on a un texte comportant $S$ symboles au total, dont la distribution a une entropie $H$. Alors la longueur du texte codé en binaire de manière optimale (par exemple par l'algorithme de Huffman) sera comprise entre $SH$ et $S(H+1)$ bits.
Exemple avec ABRACADABRA
Quelle est l'entropie correspondante ?
On a ici $S=11$ et $n=5$;
l'entropie est ${\displaystyle \frac{1}{11}\log_2 11 + \frac{1}{11} \log_2 11 + \frac{2}{11} \log_2 \frac{11}{2} + \frac{2}{11} \log_2 \frac{11}{2} + \frac{5}{11} \log_2 \frac{11}{5}}$ soit $\log_2 11- \frac{4}{11} - \frac{5}{11} \log_2 5 \simeq 2,04$ bits.
On en déduit que le nombre de bits du texte codé de façon optimale est compris entre 22,44 et 33,44 (rappel : plus haut, le code optimal fournissait 23 bits).
Pour les plus curieux : compléments sur le théorème de Shannon
On va voir en détail la preuve des inégalités de Shannon. Il y a deux ingrédients essentiels : l'inégalité de Gibbs qui concerne l'entropie et l'inégalité de Kraft qui concerne les codes préfixes. Ils permettront de construire un code binaire préfixe, le code de Shannon-Fano, qui est un code non forcément optimal, mais plus facile à décrire que le code de Huffman.
Premier ingrédient : l'inégalité de Gibbs.
Inégalité de Gibbs
Soient $(f_i)_{1\leq i \leq n}$ et $(g_i)_{1\leq i \leq n}$ des réels positifs tels que $\sum_{i=1}^n f_i = 1 $ et $\sum_{i=1}^n g_i \leq 1$. Alors $-\sum_{i=1}^n f_i \log_2 f_i \leq -\sum_{i=1}^n f_i \log_2 g_i$.
En particulier, en l'appliquant au cas où pour tout $ 1\leq i \leq n, g_i = \frac{1}{n}$, on obtient
$-\sum_{i=1}^n f_i \log_2 f_i \leq \log_2 n$.
(Remarque : si l'un des $f_i$ est nul, on prolonge par continuité en posant $0\log(0) = 0$ et l'inégalité reste vraie}
On cherche le signe de $$-\sum_{i=1}^n f_i \ln f_i +\sum_{i=1}^n f_i \ln g_i =\sum_{i=1}^n f_i \ln (g_i/f_i)$$
Pour cela on utilise la concavité du logarithme, dont la courbe est au dessous ses tangentes, en particulier au point d'abscisse 1 : on a donc pour tout réel $x$ positif $\\
ln(x) \leq (x-1)$.
On en déduit $\sum_{i=1}^n f_i \ln (g_i/f_i) \leq \sum_{i=1}^n f_i (g_i/f_i -1) \leq 0$.
Deuxième ingrédient : l'inégalité de Kraft.
Elle permet de quantifier le fait, un peu intuitif, que si un code est préfixe, les longueurs de ses mots ne peuvent pas toutes être trop petites (dit autrement, si on veut raccourcir les codes de certains symboles, il va falloir en rallonger d'autres).
Inégalité de Kraft
On considère un code binaire préfixe pour $n$ symboles. On note $(l_i)_{1\leq i \leq n}$ les longueurs des mots de ce code. On a alors $\sum_{i=1}^n 2^{-l_i} \leq 1$. Réciproquement, si $n$ réels positifs $(l_i)_{1\leq i \leq n}$ vérifient $\sum_{i=1}^n 2^{-l_i} \leq 1$, alors il existe un code binaire préfixe comportant $n$ mots dont les longueurs sont les $(l_i)_{1\leq i \leq n}$.
Cette inégalité est souvent utilisée par sa contraposée : par exemple, $2^{-4} + 2^{-3} + 2^{-3} + 2^{-2} + 2^{-2} + 2^{-2} >1$.
Donc il n'existe pas de code préfixe contenant des mots de longueur $(2,2,2,3,3,4)$ (essayez de construire l'arbre, vous verrez que vous n'y arriverez pas).
Preuve de l'inégalité de Kraft.
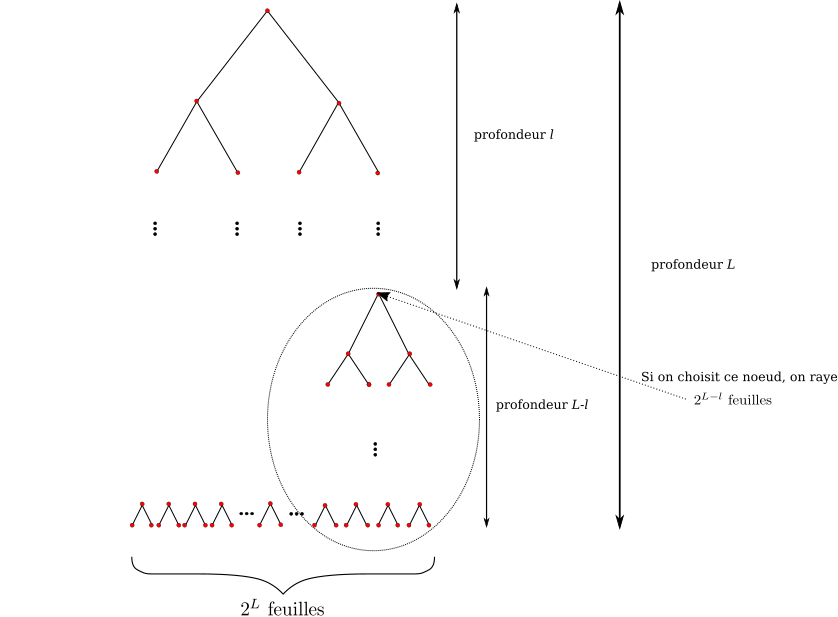
Soit un code préfixe comportant $n$ mots. On note $L$ la plus grande des longueurs des mots du code. On place les mots du code sur un arbre binaire comme expliqué plus haut. On complète de plus l'arbre en rajoutant éventuellement des nœuds, pour que les feuilles soient toutes à la profondeur $L$ : on a ainsi un arbre dit parfait de hauteur $L$, avec $2^{L}$ feuilles.
Le code étant préfixe, chacune de ces feuilles a parmi ses ancêtres au maximum un mot du code. De plus, un mot du code de longueur $l$ aura $2^{L-l}$ descendants parmi ces feuilles : en effet ce sont tous ses descendants sur $L-l$ générations. Dit autrement, on peut considérer ce mot comme la racine d'un arbre binaire de profondeur $L-l$.
Ainsi, $\sum_{i=1}^n 2^{L-l_i} \leq 2^{L}$, donc $\sum_{i=1}^n 2^{-l_i} \leq 1$.
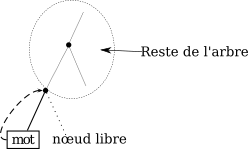
Réciproquement, pour montrer l'existence, on procède de manière analogue. On commence par construire l'arbre binaire parfait de hauteur $L$. On va placer les mots sur l'arbre par ordre croissant de longueur. À chaque fois qu'on place un mot (de longueur $l$), on raye tous ses descendants, c'est-à-dire tout le sous-arbre dont il est racine, soit $2^{L-l}$ feuilles finales de l'arbre complet initial. On est ainsi assuré qu'on obtiendra bien un code préfixe.
Le fait que les longueurs vérifient $\sum_{i=1}^n 2^{L-l_i} \leq 2^{L}$ garantit qu'à chaque étape, on n'a pas effacé toutes les feuilles finales. C'est donc bien qu'il reste toujours à chaque étape un nœud non effacé que l'on peut choisir comme mot du code.
La figure ci-dessous illustre cette construction.
Preuve des inégalités de Shannon :
On est maintenant en mesure de montrer que le nombre de bits du texte codé est supérieur à $SH$, ce qui était l'une des inégalités de Shannon. En effet, les longueurs du code optimal vérifient donc $\sum_{i=1}^n 2^{-l_i} \leq 1$. En posant $g_i = 2^{-l_i}$ et en appliquant l'inégalité de Gibbs, on obtient alors $$-\sum_{i=1}^n f_i \log_2 f_i \leq -\sum_{i=1}^n f_i \log_2 (2^{-l_i}),$$ soit $H \leq \sum_{i=1}^n f_i l_i$. Or le nombre total de bits est $S\sum_{i=1}^n f_i l_i$.
De plus l'inégalité de Kraft permet de prouver l'existence d'un code préfixe, qui ne sera en général pas optimal, mais presque. En effet, si on pose $l_i = \lceil-\log_2(f_i)\rceil $, on a bien
$$\sum_{i=1}^n 2^{-l_i} \leq \sum_{i=1}^n 2^{\log_2 f_i} = \sum_{i=1}^n f_i = 1.$$
L'inégalité de Kraft garantit donc l'existence d'un code binaire préfixe ayant les $(l_i)$ comme longueurs de mots1.
Le texte ainsi code a une longueur de $$\sum_{i=1}^n Sf_il_i \leq \sum_{i=1}^n Sf_i(-\log_2 f_i+1) = S(H+1)$$ bits. On est donc assuré que le code optimal fera mieux que cela, et on obtient ainsi la deuxième inégalité de Shannon.
Références
1. Wikipedia : https://fr.wikipedia.org/wiki/Codage_de_Huffman
2. Images des Maths : http://images.math.cnrs.fr/Claude-Shannon-et-la-compression-des-donnees