Comment les bases de dénombrement vues en Terminale se manifestent-elles dans des procédés de synthèse industriels ? Voyage au pays de la chimie combinatoire.
Introduction
Synthétiser (c'est-à-dire créer ou recréer en laboratoire) des molécules possédant une propriété biologique intéressante permet de les incorporer à une production à grande échelle de médicaments utilisant ce principe actif.
En pratique, il est impossible de synthétiser une macromolécule1 naturelle complexe comme un enzyme2. On se contente de synthétiser un mime plus petit en identifiant le site actif de l'enzyme qui constitue la zone responsable de son effet biologique.
Dans les années 1990, une nouvelle façon de synthétiser des molécules originales connaît un essor important : la chimie combinatoire 3. Il s'agit d'un ensemble de techniques permettant de générer un panel de molécules, appelé bibliothèque, constituées d'un enchaînement variable et diversifié de blocs constitutifs.
La chimie combinatoire peut se résumer à trois grandes étapes :
- la préparation de la bibliothèque,
- le passage en revue (dit "screening") des composés pour détecter ceux qui possèdent des propriétés biochimiques recherchées via un test de sélection simple,
- la détermination de la structure des composés actifs sélectionnés par l'étape de screening.
Préparation de la bibliothèque
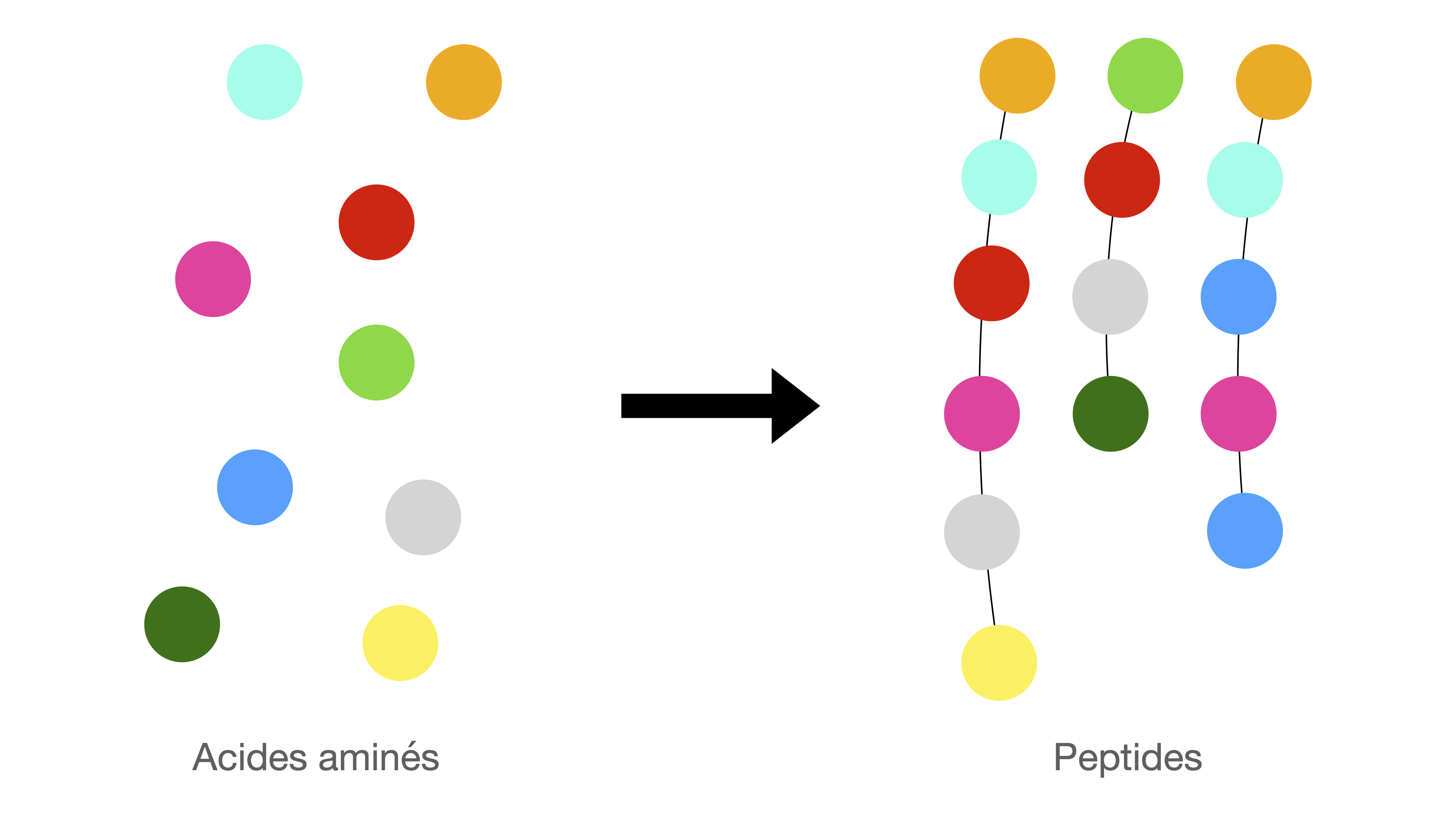
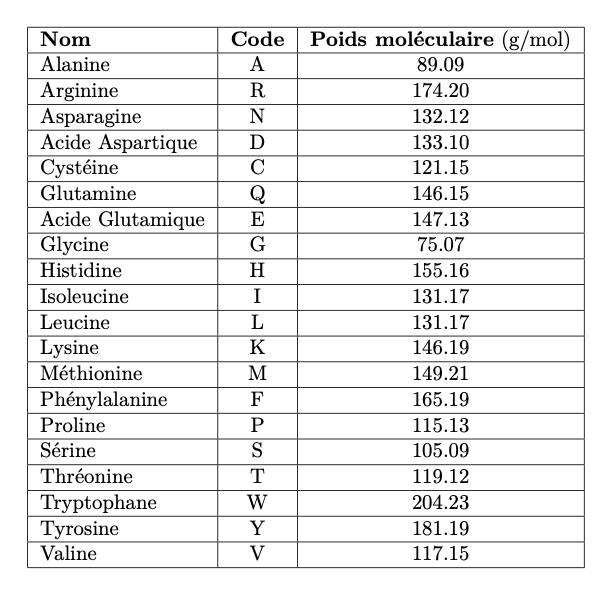
Les mimes dont nous parlerons ici sont des petits peptides : il s'agit d'assemblages de blocs constitutifs ressemblant à des colliers de perles où chaque perle correspond à un acide aminé1 (Figure 1). Une lettre est attribuée à chacun des $24$ acides aminés naturels (Figure 5).
Les acides aminés sont des unités structurelles : un enchaînement d'une dizaine d'acides aminés reliés entre eux par des liaisons peptidiques s'appelle un peptide. Une plus longue chaîne s'appelle une protéine.
Les peptides sont synthétisés sur un support solide de la forme d'une bille d'environ $1$ mm de diamètre. Sur cette bille peut être greffé à partir d'une base moléculaire un nombre conséquent d'exemplaires d'un même peptide de la bibliothèque. Chaque bille est donc porteuse d'une unique séquence peptidique présente en de multiples exemplaires. Le support solide permet d'isoler facilement les peptides présentant une activité biologique révélée lors du test de sélection.
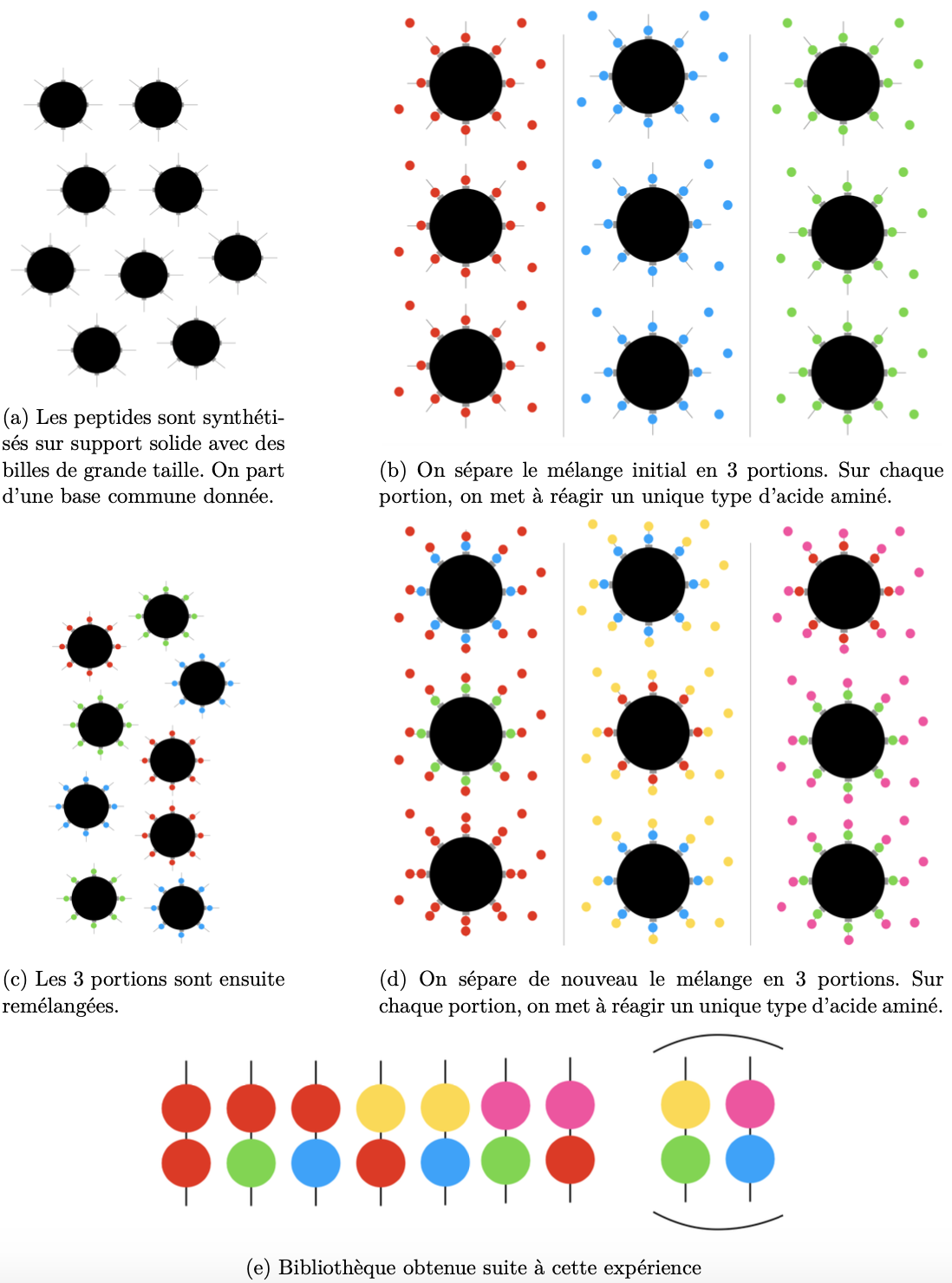
On part d'une base commune donnée.
Pour ajouter un premier acide aminé sur cette base, on sépare le mélange initial en $p$ portions. Sur chaque portion, on met à réagir un unique type d'acide aminé.
Les $p$ portions sont ensuite remélangées.
Pour ajouter un deuxième acide aminé, on sépare le mélange précédent en $q$ portions. Sur chaque portion, on met à réagir un unique type d'acide aminé.
Les $q$ portions sont ensuite remélangées, etc.
Ce procédé itératif de synthèse, qu'illustre la Figure 2, permet de générer à moindre coût un très grand nombre de molécules différentes.
Imaginons qu'on veuille synthétiser un peptide qui aurait finalement la structure générale ci-dessous (Figure 3). On souhaite explorer l'impact biologique de la nature des acides aminés aux positions $2,3$ et $6$ en testant $6$ différents acides aminés sur ces positions : $G$, $D$, $E$, $H$, $R$, $Y$.
On met à réagir la base (en de multiples exemplaires) avec un premier acide aminé (représenté ci-dessus en vert). Puis on sépare le mélange en $6$ portions et on met à réagir l'acide aminé $G$ sur la première portion, $D$ sur la deuxième portion, etc. On remélange. Puis on sépare de nouveau le mélange en $6$ portions et on fait réagir la première portion l'acide aminé $G$, $D$ sur la deuxième portion, etc. Et ainsi de suite.
Combien de peptides différents peut-on générer par cette synthèse itérative ?
Il s'agit ici de savoir combien il y a de $3-$listes créées à partir d'un ensemble comportant $6$ éléments. Une bibliothèque complète comporterait ici $6^3$, c'est-à-dire $216$ peptides différents.
En réalité et dans le cadre d'une expérience donnée, une bibliothèque conçue en laboratoire peut comporter des milliers de peptides 1.
À la recherche des peptides prometteurs par spectrométrie de masse
Screening
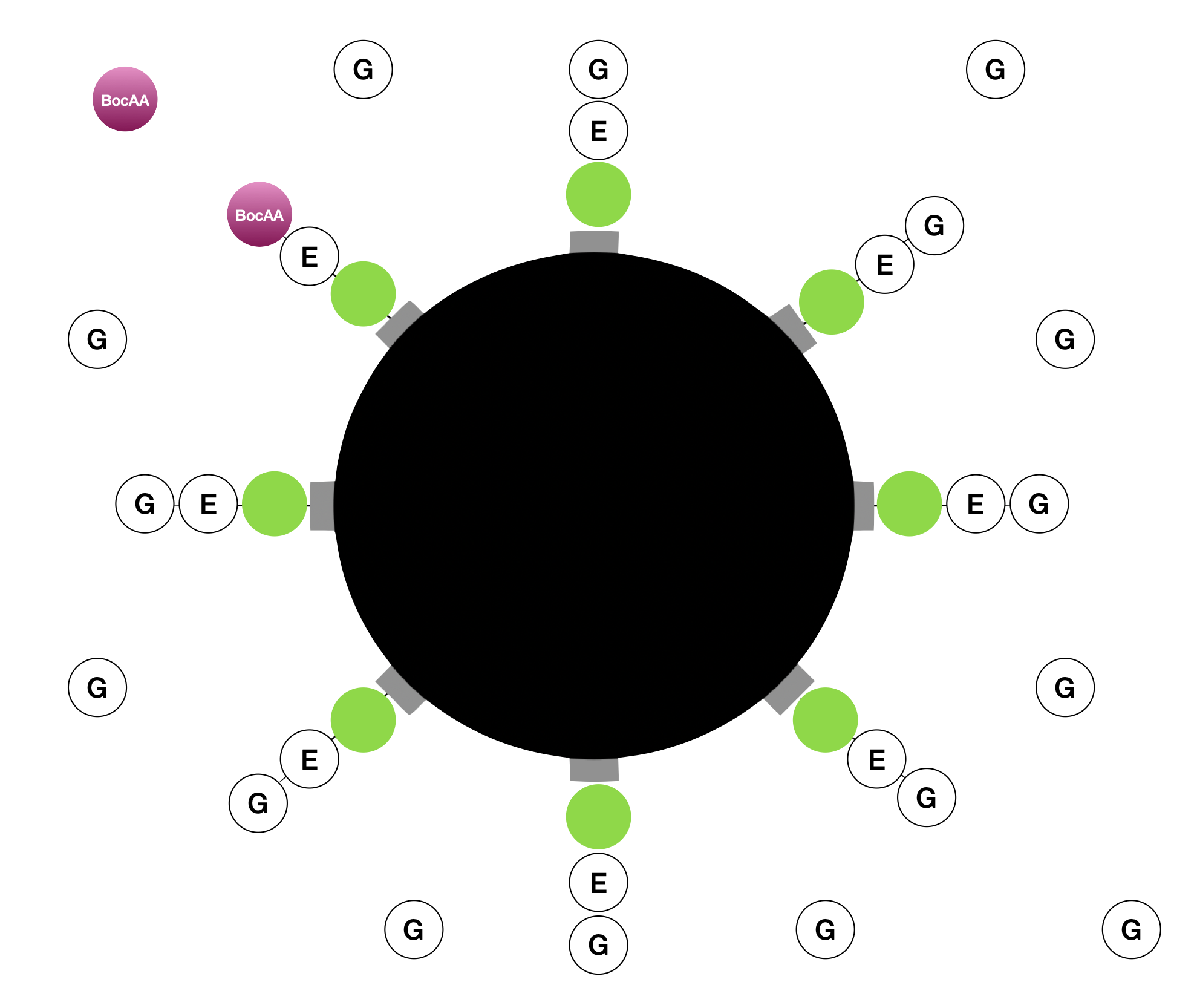
Une fois la bibliothèque créée, la phase de screening, illustrée par la Figure 4, permet d'isoler les peptides synthétisés qui possèdent les propriétés biochimiques recherchées via un test simple.
Ici les billes sont coulées dans un gel sur lequel est ajoutée une solution révélatrice. Le gel est soumis à irradiation UV pour révéler les billes actives autour desquelles un halo jaune est présent. Les peptides sélectionnés sont alors clivés de la bille.
Mais comment savoir quelle est la structure du peptide prometteur ?
Déterminer la structure d'un peptide prometteur nécessite de réussir à :
- Identifier les acides aminés le constituant, parmi ceux qui sont variables : on appellera le résultat de cette analyse l'alphabet. Il s'agit d'une liste non ordonnée de lettres, pouvant se répéter. Par exemple,
\[ [G, \; G, \; D ] \quad [E, \; E, \; E]\quad [H, \; R, \; Y ] \quad ... \] sont des alphabets possibles pour le peptide représenté sur la Figure 3. - Identifier, parmi toutes les séquences possibles découlant de l'alphabet, celle du peptide prometteur. Par exemple, pour l'alphabet $[G, \; G, \; D]$, il y a trois combinaisons possibles : $GGD$, $GDG$ et $DGG$, qui correspondent à trois peptides différents.
Identifier les acides aminés composant le peptide prometteur
Les chimistes utilisent la spectrométrie de masse pour déterminer la composition du peptide prometteur, c'est-à-dire l'alphabet.
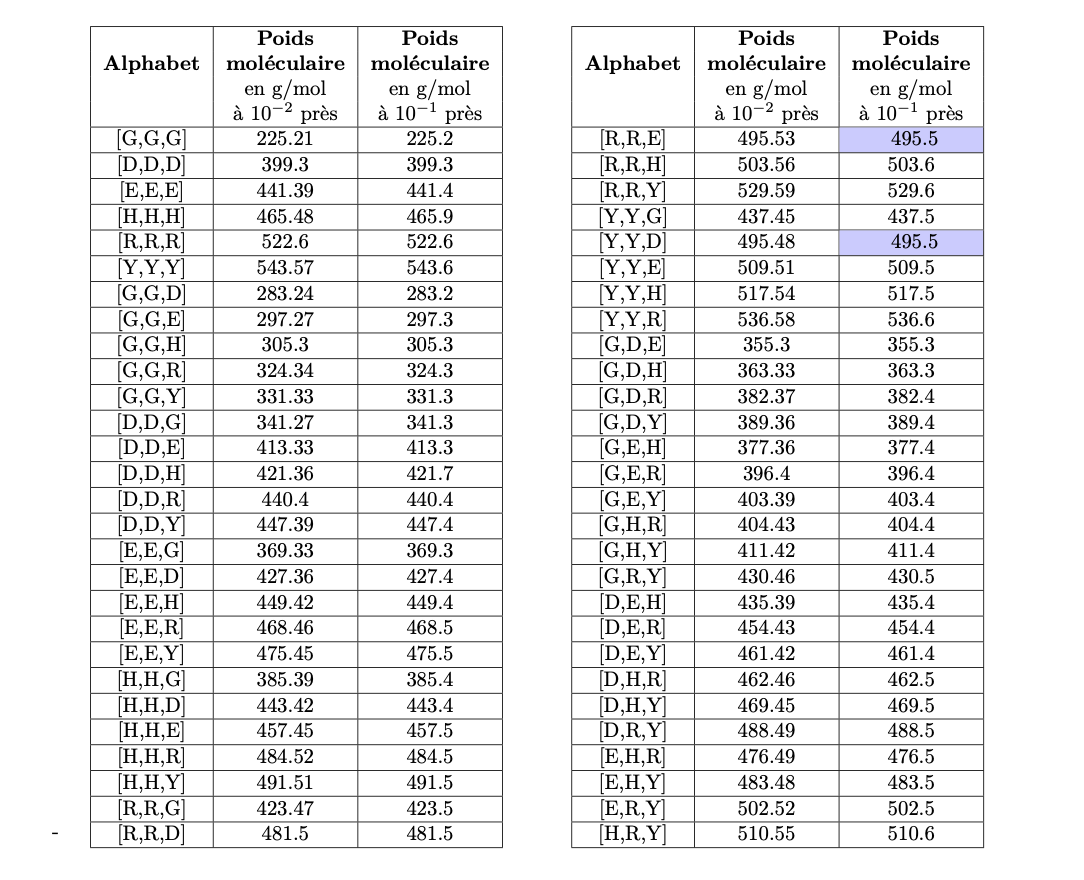
En effet, les poids moléculaires de chaque acide aminé étant connus (Figure 5), il est possible de retrouver les différents blocs composant le peptide à partir d'une analyse de masse. Dans un spectromètre de masse, on mesure le temps mis par une particule (ici, un peptide) chargée pour atteindre un détecteur situé à une distance connue. Les particules les plus lourdes sont moins rapides. On obtient la masse du peptide à partir de ce temps de vol.
Imaginons un exemple très simple : on synthétise trois sortes de peptides en faisant réagir un début de chaîne donné avec trois acides aminés différents : $G$, $D$ et $E$. Ces trois acides aminés ayant trois poids moléculaires distincts, l'application \[ f: \begin{array}{lll}\mathscr{A} &\to &\mathscr{M} \\ alphabet &\mapsto &masse \; du \; peptide\end{array} \] réalise une bijection de l'ensemble $\mathscr{A}$ correspondant à l'ensemble des alphabets possibles (ici $\mathscr{A}=\left\{[G],[D],[E]\right\}$) sur l'ensemble $\mathscr{M}$ contenant les masses distinctes des $3$ peptides. Ainsi, une analyse de spectrométrie de masse fournira directement par correspondance bijective la composition du peptide prometteur.
Reprenons maintenant l'exemple précédent d'un peptide comportant $8$ acides aminés dont ceux en positions $2,3$ et $6$ sont tous les trois choisis dans l'ensemble $\{G,D,E,H,R,Y\}$ (représenté sur la Figure 3). Ces $6$ acides aminés ont bien $6$ poids moléculaires distincts, mais peut-on en dire autant des différents alphabets qui en découlent ?
Autrement dit, l'application $f$ précédente est-elle toujours bijective ?
$f$ est bijective à condition que les ensembles $\mathscr{A}$ et $\mathscr{M}$ aient le même cardinal.
Calculer le cardinal de $\mathscr{A}$ est un exercice en soi intéressant. Une première approche consiste à remarquer que $\mathscr{A}$ est l'union disjointe de $3$ ensembles: $\mathscr{A}= \mathscr{A}_1 \cup \mathscr{A}_2 \cup \mathscr{A}_3$ où
- $\mathscr{A}_1$ est le sous-ensemble de $\mathscr{A}$ des alphabets comportant $3$ fois la même lettre,
- $\mathscr{A}_2$ est le sous-ensemble de $\mathscr{A}$ des alphabets comportant $2$ fois la même lettre et une troisième lettre différente,
- $\mathscr{A}_3$ est le sous-ensemble de $\mathscr{A}$ des alphabets comportant comportant $3$ lettres différentes.
L'union étant disjointe, \[ \text{Card}(\mathscr{A})=\text{Card}(\mathscr{A}_1)+\text{Card}(\mathscr{A}_2)+\text{Card}(\mathscr{A}_3). \] Or $\text{Card}(\mathscr{A}_1) = 6$, $\text{Card}(\mathscr{A}_2) = 6\times 5$ et $\text{Card}(\mathscr{A}_3)=\displaystyle\binom{6}{3}$. Donc $\text{Card}(\mathscr{A})=56$.
Cette approche par partition a un défaut : elle peut devenir un peu pénible si on augmente le nombre d'emplacements où l'on veut mettre des acides aminés variables.
Une autre approche pour calculer le cardinal de $\mathscr{A}$ consiste à reconnaître qu'on dénombre ici des combinaisons avec remise 12.
Dans le cas qui nous occupe, créer un alphabet consiste :
- pour chaque acide aminé sauf un, disons $G,D,E,H,R$ dans cet ordre, prendre le nombre de "perles" de chaque sorte (ce qu'on désignera par des $\circ$) puis passer au suivant (ce qu'on désignera par un séparateur $\times$)3,
- pour le dernier acide aminé $Y$ uniquement, prendre le nombre de "perles" nécessaires (inutile de placer un séparateur à la fin).
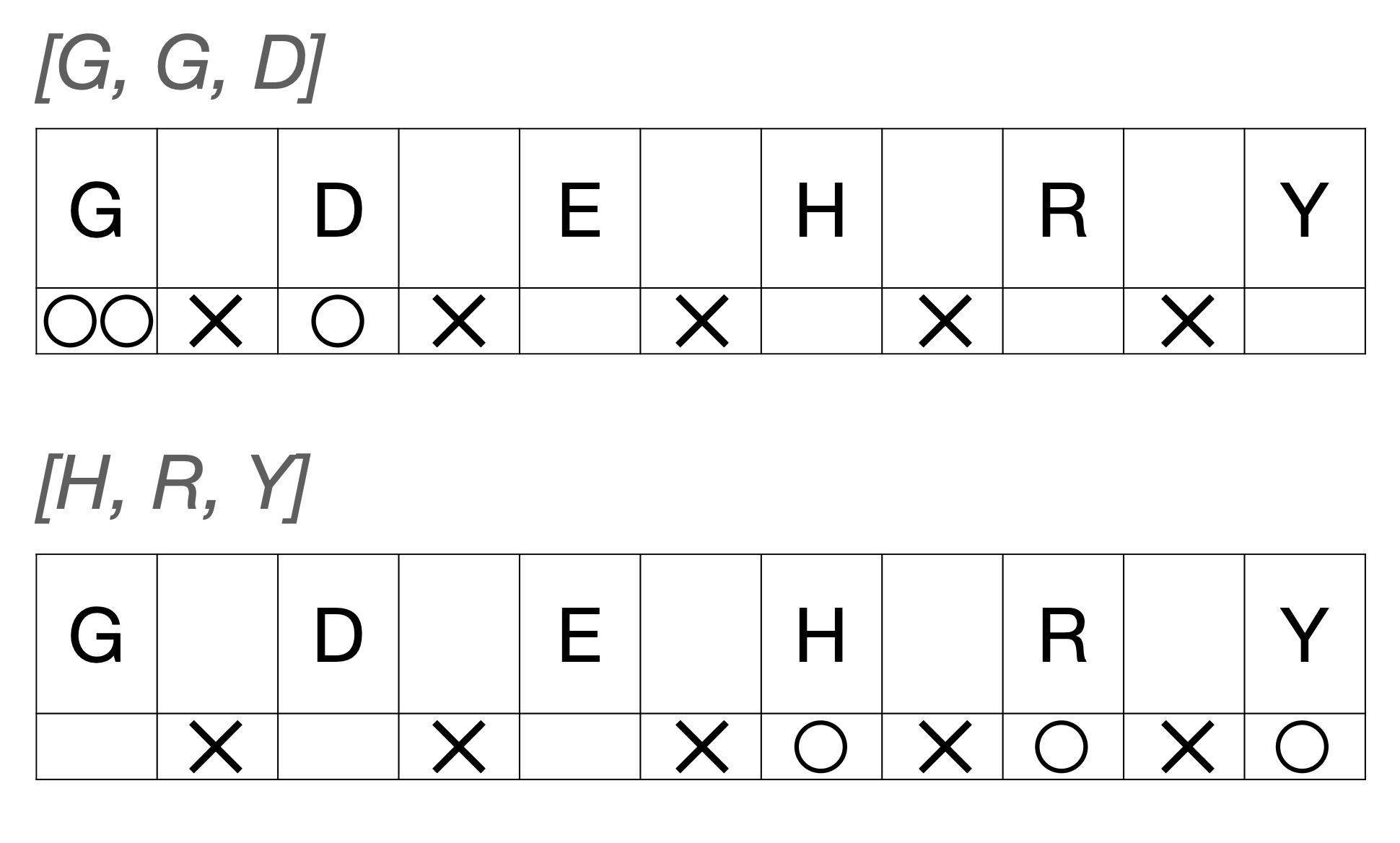
Ce processus permet de faire correspondre à chaque alphabet un enchaînement qui contient $3$ symboles $\circ$ (car les alphabets à créer sont des ensembles à $3$ éléments) et $5$ symboles $\times$ dans un ordre quelconque, donc $8$ symboles en tout.
Par exemple, l'enchaînement $\circ\circ\times \circ\times\times\times\times$ désigne l'alphabet $[G, \; G, \; D]$ et l'enchaînement $\times\times\times \circ\times \circ \times \circ$ désigne l'alphabet $[H, \; R, \; Y]$ (Figure 6).
Créer un tel enchaînement revient à choisir les emplacements des symboles $\circ$.
Il y a $\displaystyle\binom{8}{3}=56$ façons de faire cela.
L'avantage de cette deuxième méthode est qu'elle se généralise aisément. Si l'on a $k$ acides aminés à placer et qu'on a $n$ choix pour chacun d'entre eux, le cardinal de l'ensemble des alphabets possibles est $\displaystyle\binom{n+k-1}{k}$.
Pour revenir à l'exemple de notre peptide de référence, quelle que soit la méthode choisie, on trouve que $\text{Card}(\mathscr{A})=56$. Pour déterminer si chaque masse correspond bien à un unique alphabet, on peut alors effectuer les $56$ calculs de poids moléculaires correspondants et vérifier si l'on obtient $56$ résultats distincts ou non.
Une simulation informatique (Figure 7) fournit une réponse pour l'exemple qui nous occupe:
- $f$ est bijective si le spectromètre fournit des résultats précis à $10^{-2}$ g/mol près,
- $f$ n'est pas bijective si le spectromètre fournit des résultats précis à $10^{-1}$ g/mol près !
En effet, dans ce deuxième cas les peptides comportant les acides aminés $Y$, $Y$ et $D$ et ceux comportant les acides aminés $R$, $R$ et $E$ auront a priori la même masse !
Identifier la bonne séquence
Partons du principe que le spectromètre et l'alphabet choisi permettent une correspondance bijective entre la masse du peptide et sa composition.
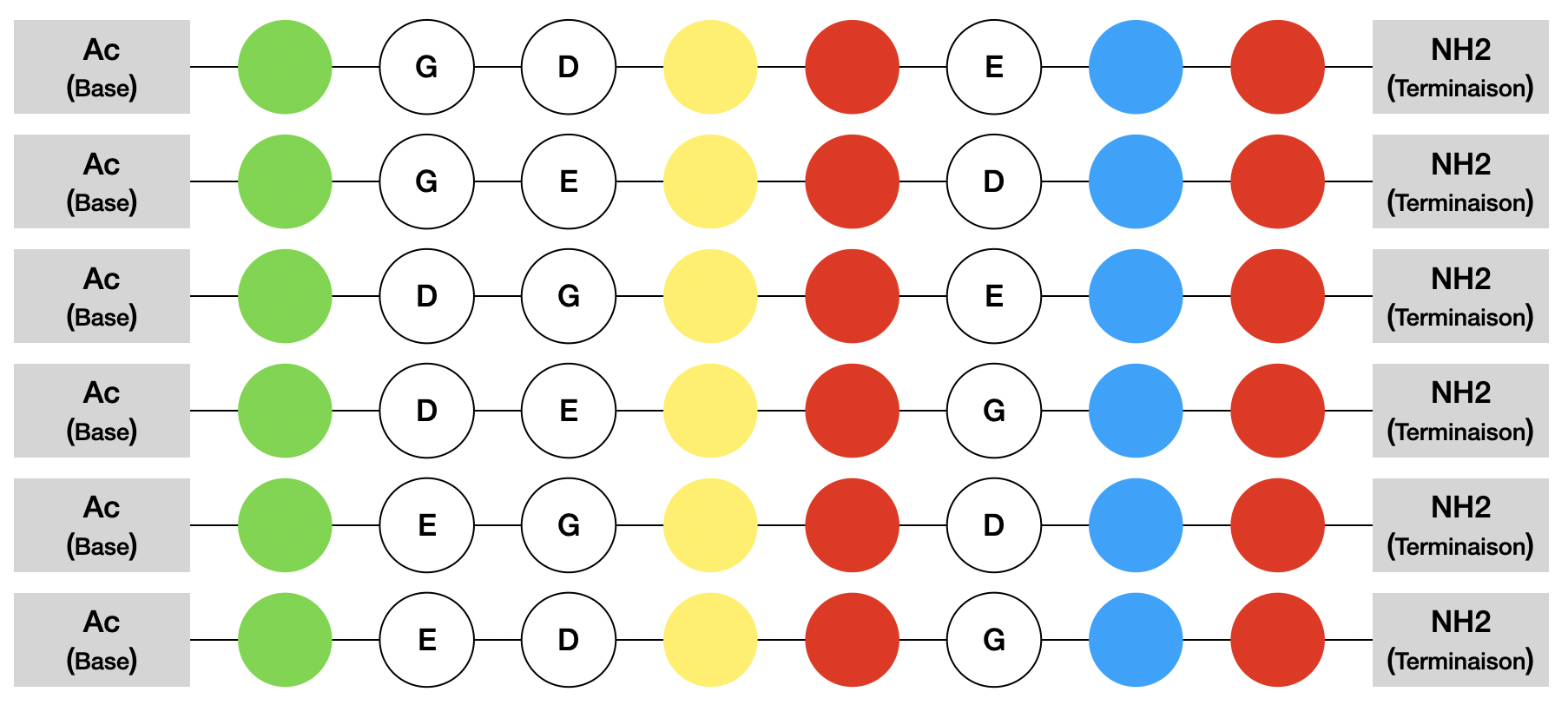
Imaginons qu'on identifie un peptide comportant les acides aminés $G$, $D$ et $E$ comme prometteur. Tous les peptides générés à partir de ces trois acides aminés sont alors suspects ! Ici il y en a $3!=6$, c'est-à-dire autant que de permutations d'un ensemble comportant $3$ éléments (Figure 8).
Comment peut-on procéder pour identifier la bonne séquence ?
Simplifions le problème en considérant un peptide comportant seulement deux acides aminés variables $G$ et $E$ : comment faire la différence entre les séquences $GE$ et $EG$ ? Les peptides correspondants sont générés à partir du même alphabet donc ont la même masse.
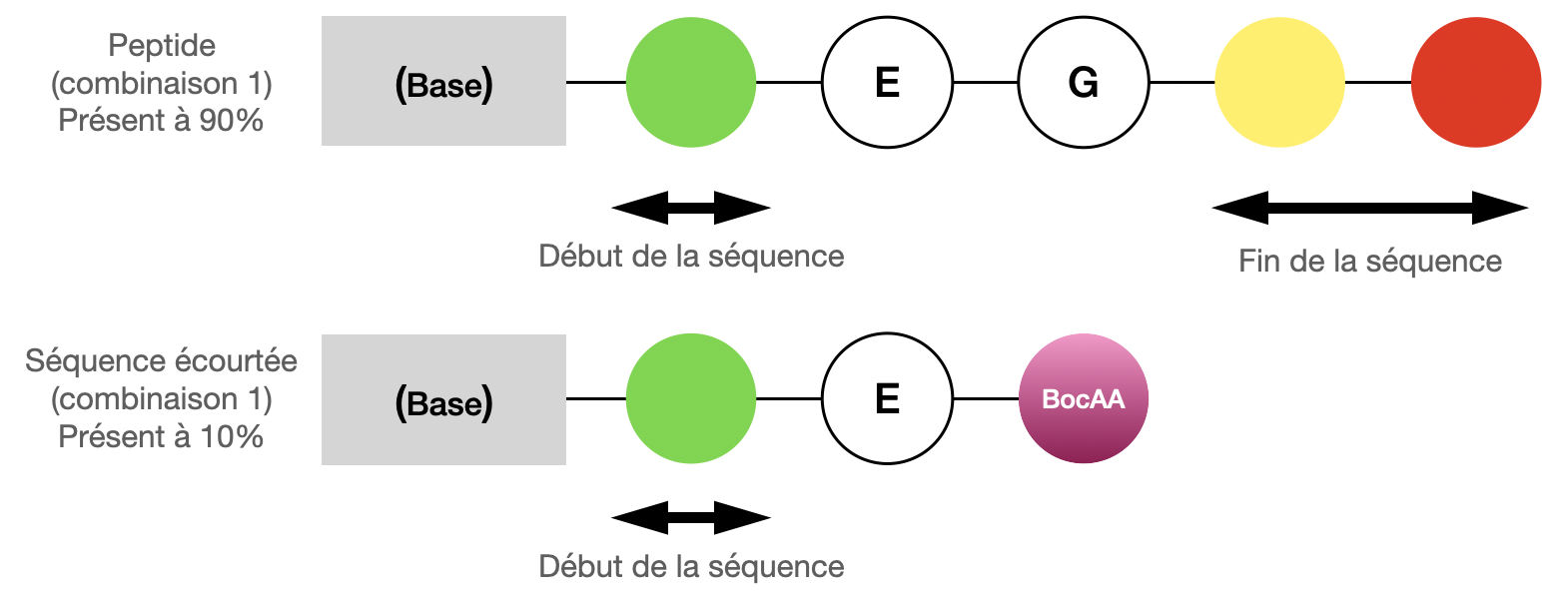
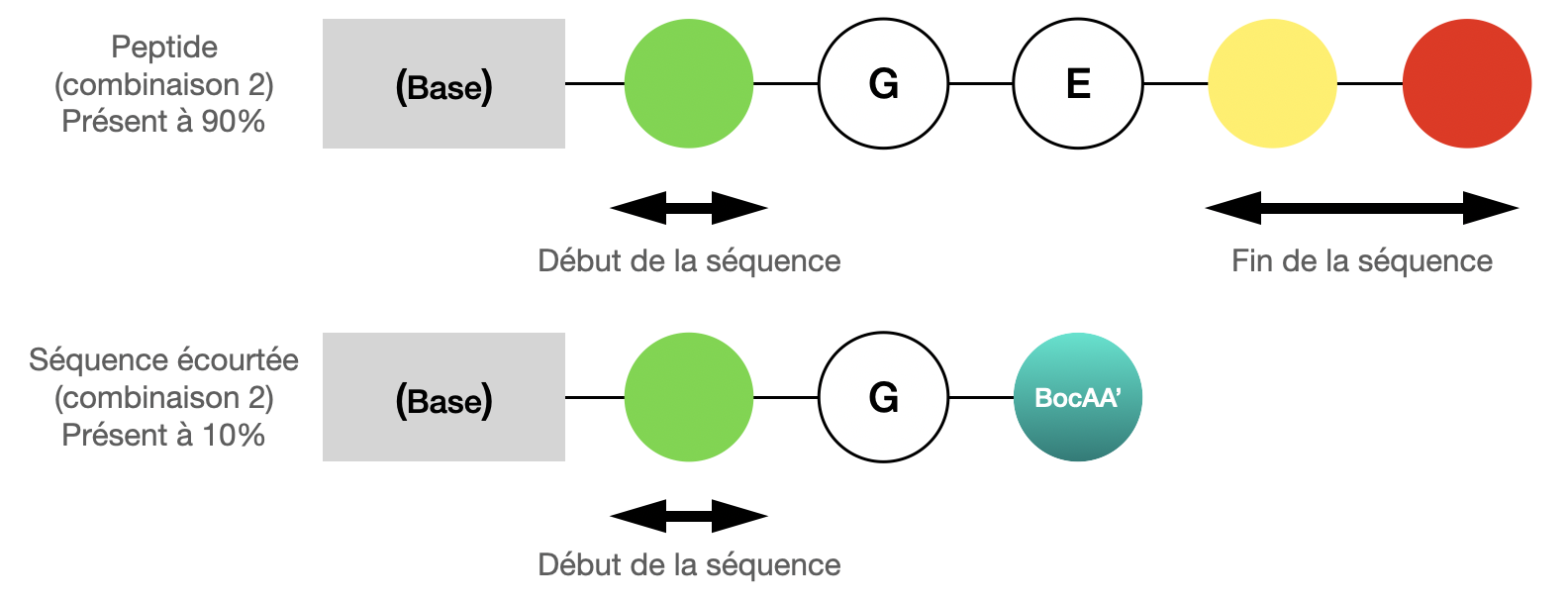
Les chimistes ont eu l'idée suivante : introduire, lors de la synthèse, une petite proportion de "bloquants" dans la synthèse des peptides (Figure 9). En mettant dans le spectromètre de masse les billes portant les peptides correspondants à la séquence $EG$, seulement $90\%$ seront effectivement de ce type et $10\%$ seront de la forme $EBocAA$, où $BocAA$ est un "bloquant" permettant d'identifier l'unique combinaison $EG$ (Figure 10).
On introduit lors de la synthèse une petite proportion de "bloquants" (ici $BocAA$) mélangée avec les acides aminés (ici $G$).
De même, parmi les peptides correspondants à la séquence $GE$, seulement $90\%$ sont effectivement de ce type et $10\%$ sont de la forme $GBocAA'$, où $BocAA'$ est un autre "bloquant" (Figure 11).
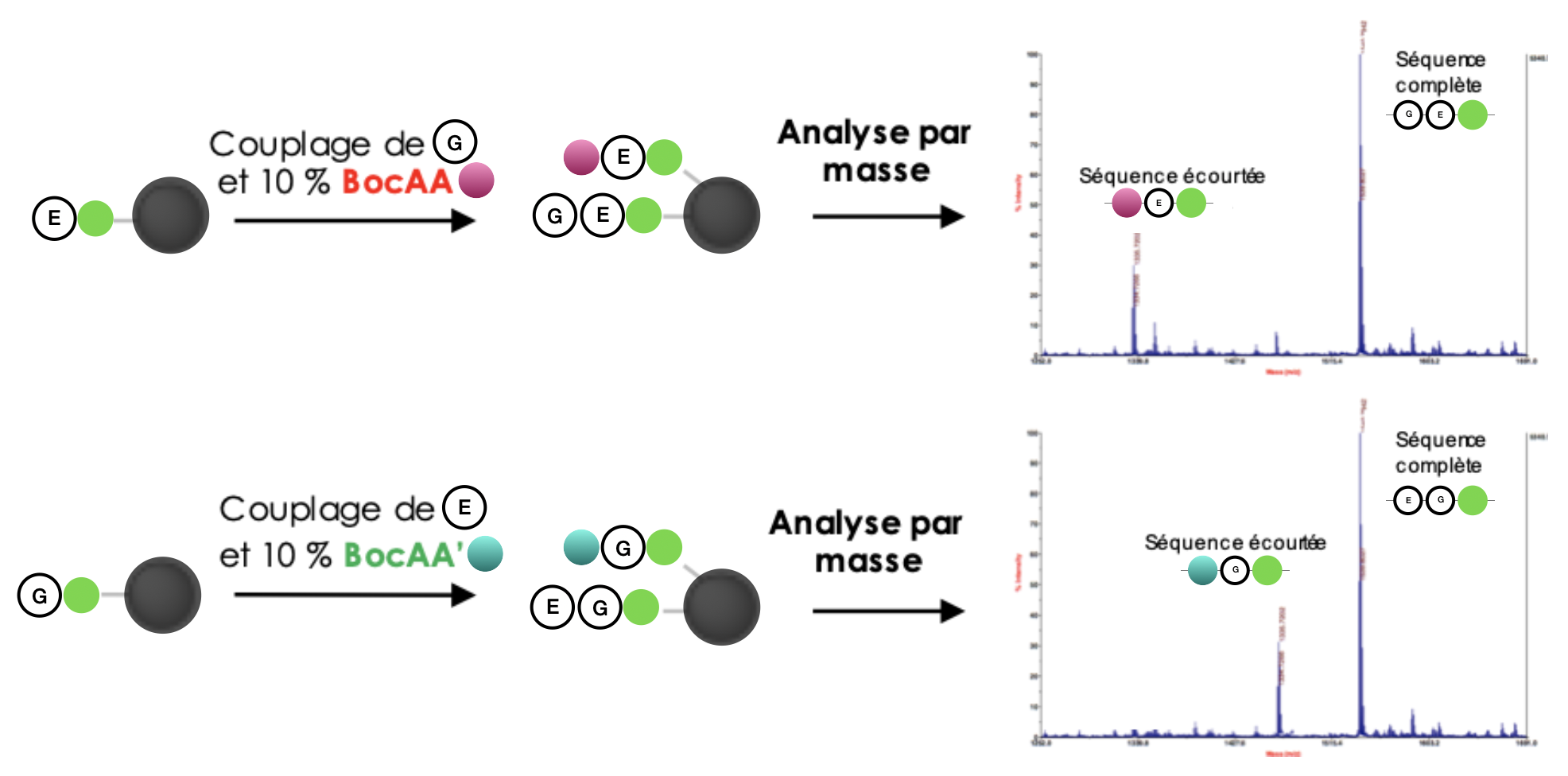
Les peptides correspondant aux séquences $EG$ et $GE$ ont certes la même masse mais sont mélangés à des séquences écourtées ($EBocAA$ ou $GBocAA'$) qui elles n'ont pas la même masse. Le spectromètre fournit alors une analyse comportant deux pics (Figure 12). Chaque pic correspond au temps de vol d'un des deux types de peptides alors présents dans le spectromètre (avec ou sans bloquant). Le plus grand pic permet d'identifier l'alphabet (ici : $[G, \; E]$) : c'est ce que nous avons déjà développé dans la partie précédente. Le plus petit, conséquence de la présence d'un bloquant, permet de discriminer les différentes séquences possibles.
Ce recours aux bloquants peut être étendu à l'identification de l'alphabet lorsque l'application $f:\mathscr{A}\to \mathscr{M}$ n'est pas bijective, notamment du fait de la précision du spectromètre utilisé.
Conclusion
Dans un contexte industriel où la question du temps et de l'argent est devenue primordiale, le recours à la chimie combinatoire permet de maximiser les chances d'obtenir des molécules performantes pouvant satisfaire des essais cliniques ultérieurs. La part de hasard introduite par cette méthode vient compléter la fine analyse structurale du chimiste organicien et permet la découverte de nouveaux médicaments que la raison seule n'aurait pu trouver.
Remerciements
Merci à Amandine Vincent de m'avoir parlé de ses travaux de thèse, qui ont inspiré cet article.