Cliquez sur chacune des images du texte pour avoir accès au diaporama sonore qui lui correspond !

Le théorème de Pythagore

Vous connaissez bien sûr ! Comme tous ceux qui ont entendu parler de mathématiques, depuis une bonne trentaine de siècles au bas mot. Forcément, je n'ai rien de nouveau à vous raconter. Tout et son contraire a été dit, des siècles après la mort de Pythagore, par des auteurs qui ne disposaient d'aucun document, et qui n'en parlaient que par ouï-dire. Pourquoi le répéter alors ? Avouons-le, c'est un prétexte pour vous présenter quelques unes des ressources du site Histoires de Mathématiques. Chacune des images qui suivent porte un lien vers le site et ses récits audio. Ils se lancent soit automatiquement, soit en passant la souris vers le bas de l'image. Depuis la racine, les pdf des mêmes histoires peuvent aussi être téléchargés.

Pythagore au fond, qui était il ? Plus probablement un gourou qu'un géomètre, plutôt un mystique qu'un scientifique ; en tout cas un fabriquant de miracles plus ou moins arrangés. Sa religion a duré une bonne dizaine de générations, ce qui n'est pas rien tout de même. Que disait elle ? Que tout est nombre, en ce bas monde, et même au-delà. « J'en jure par celui qui grava dans nos cœurs la Tétrade sacrée, immense et pur symbole, source de la Nature et modèle des Dieux. »

La Tétrade sacrée c'est plus que le nombre 10 : c'est la figure triangulaire formée de 1, puis, 2, puis 3, puis 4 jetons. S'il y a bien un héritage dont on puisse être à peu près sûr qu'il nous vienne de Pythagore, c'est celui-là : les nombres polygonaux vus comme des figures géométriques discrètes. Prenez par exemple les nombres carrés. Pour passer d'un nombre carré au suivant, il faut le flanquer d'un « gnomon », ou une équerre si vous préférez, comme sur la figure ci-dessous:

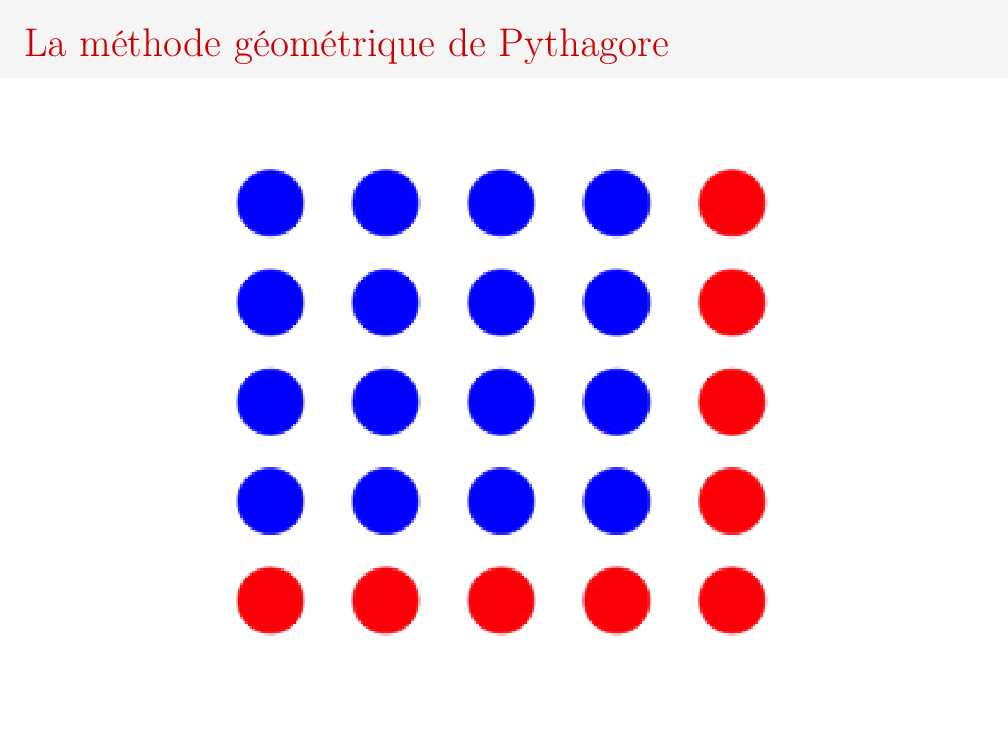
S'il arrive que le gnomon soit lui-même un nombre carré, alors on a construit un « triplet pythagoricien ». Il n'est pas exclu que pour Pythagore, son fameux théorème se soit réduit à cela: une manière de fabriquer des triplets d'entiers comme 3, 4, 5, tels que la somme des carrés des deux plus petits soit égal au carré du plus grand. Il y a peu de chances que Pythagore ait inventé la méthode. La tablette Plimpton 322 est la preuve que ces triplets étaient connus un bon millénaire auparavant. De même que leur interprétation géométrique comme les côtés d'un triangle rectangle : elle figure dans les Shulba-Sutras hindous. On a bien retrouvé le triangle 3,4,5 chez les Égyptiens, mais aucune trace de la fameuse corde à 13 nœuds censée le matérialiser.

Il est tout de même probable que Pythagore connaissait le résultat général dans les triangles rectangles, et qu'il le savait très ancien. Mais pouvait-il le démontrer ? On l'ignore, car on ne sait même pas quel sens pouvait avoir pour lui la notion de démonstration.

Au vu des figures retrouvées sur des tablettes mésopotamiennes, et aussi selon le témoignage de Platon dans le Ménon, il est probable que le cas particulier du triangle rectangle isocèle, démontré par réarrangement de pièces de tangram, soit connu de longue date.

        

Quand a-t-on étendu ce jeu de tangram au cas général, comme dans ce manuel de certificat d'études ? On l'ignore.

Il n'est absolument pas prouvé que cette démonstration, la plus simple et la plus visuelle, soit la première de l'histoire. En tout cas, ce n'est pas celle que propose Euclide dans les Éléments I.47.

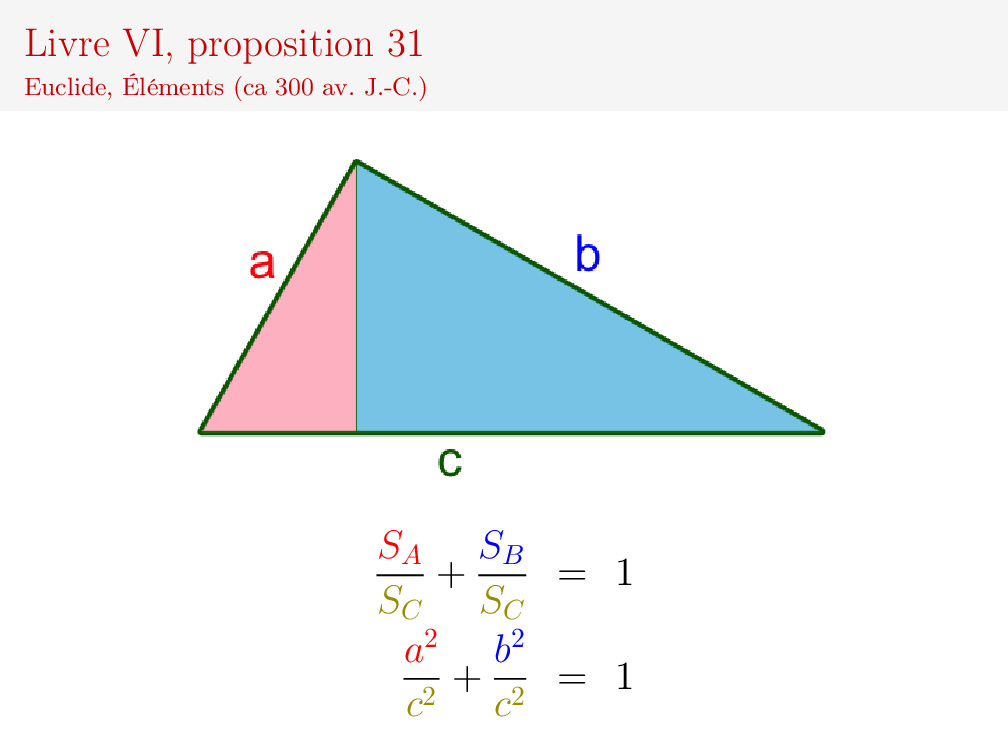
Nombreux sont ceux qui ont reproché à Euclide l'obscurité de sa démonstration, sa « brillante absurdité » selon Schopenhauer. Ils n'avaient pas dû dépasser le premier livre ! On trouve dans les Éléments VI.31 le véritable « théorème de Pythagore », celui qui explique de façon lumineuse que le résultat porte en fait sur des rapports d'aires dans trois triangles semblables. Dommage qu'il ne soit pas plus enseigné !

En parlant d'enseignement, quels exercices a-t-on posé au fil du temps sur le théorème de Pythagore ? Les énoncés sont remarquablement homogènes : de la Mésopotamie à l'Europe, en passant par la Chine, l'Inde, la Perse, al-Andalus…, il a toujours été question d'échelles qui glissent le long d'un mur, de bambous brisés et de cordes que l'on tend. Il n'y aucune raison pour que ces problèmes marchent moins bien dans nos classes !

Certes, mais aurait-on par hasard plus utile à proposer à nos élèves que le temps de vol d'un faucon poursuivant un rat ? plus crédible comme application que deux mendiants en lévitation ? Oui : le fondement des calculs trigonométriques. La figure suivante représente un secteur angulaire tel que le voyaient les Indiens.

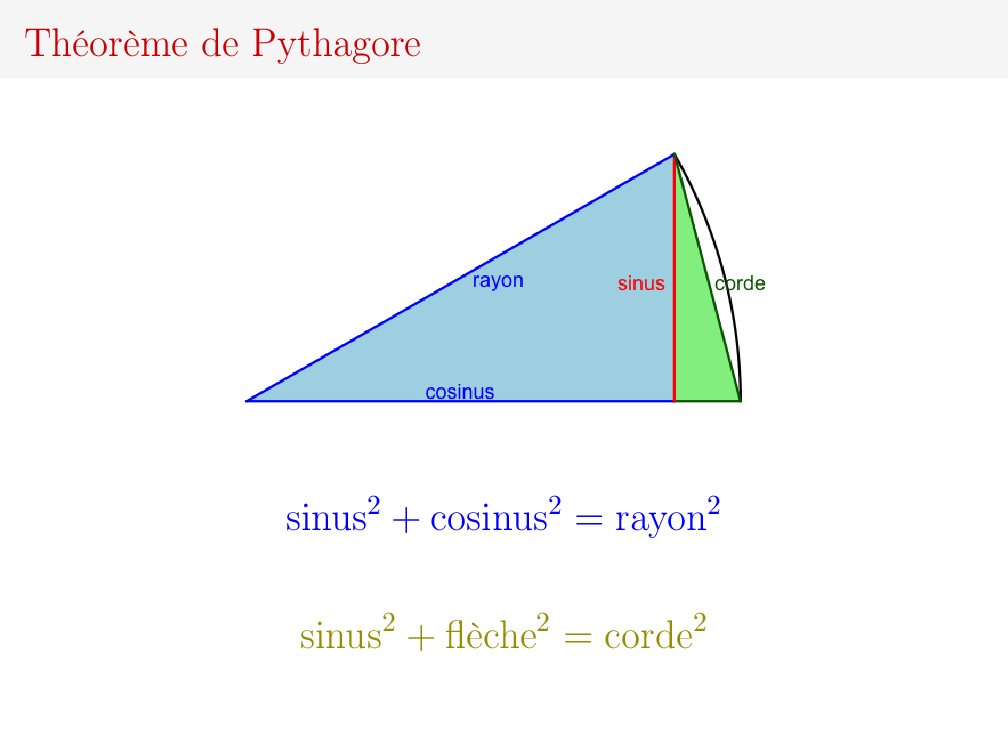
L'application du théorème de Pythagore dans le triangle bleu donne la relation entre le rayon, le sinus, et le cosinus qui est le sinus du complémentaire. Dans le triangle vert, la formule relie le sinus, la flèche qui est la différence du rayon et du cosinus, et la corde, qui est le double du sinus de l'angle moitié. En partant du sinus d'un angle, on peut donc obtenir le sinus de l'angle moitié. Il n'en fallait pas plus à Aryabhata pour calculer sa table de sinus de 24 angles.

Il était loin d'être le premier. L'opération consistant à diviser de façon itérée les côtés d'un polygone régulier est la base de la méthode d'exhaustion, qui remonte à Eudoxe de Cnide. Utilisée par Euclide dans les Éléments XII.2, elle a servi à Archimède pour son encadrement spectaculaire de la valeur de $\pi$.

C'est encore la même application du théorème de Pythagore à la division des angles, qui conduit à la célèbre formule de Viète, vue par certains comme le coup d'envoi de l'analyse moderne. La voici dans le texte original, et sous forme moderne.

        

C'est vous dire la richesse de l'héritage pythagoricien. Et encore, je ne vous ai parlé que de son théorème. Il me resterait encore à évoquer sa philosophie alimentaire, sa cosmologie, sans oublier sa théorie de l'harmonie musicale…

Références : le dernier transparent de chaque histoire porte les cinq ou six références que j'ai le plus utilisées pour l'écrire. En voici quelques autres :

Alain BERNARD Brigitte ROUSSEL (2011) Quelles démonstrations pour le théorème de Pythagore ?
IREM de la Réunion

Karine CHEMLA éd. (2012) The History of Mathematical Proof in Ancient Traditions
Cambridge University Press

Éliane COUSQUER (2010) Histoire du théorème de Pythagore
mediamaths

Jöran FRIBERG (2007) Amazing Traces of a Babylonian Origin in Greek Mathematics
World Scientific Publishing

Robert HAHN (2017) The Metaphysics of the Pythagorean Theorem
SUNY Press

Jens HØYRUP (2010) L'algèbre au temps de Babylone
Paris : Vuibert

Agathe KELLER (2006) Expounding the mathematical seed (2 vols.)
Basel: Birkhäuser

Elisha S. LOOMIS (1968) The Pythagorean Proposition
Classics in Mathematics Education Series

Patrick ROUSEL (2011) The complete Pythagoras
Holybooks

Helain SELIN éd. (2000) Mathematics across cultures
Springer, New York

Bernard VITRAC (2005) Les géomètres de la Grèce antique
CultureMATH