Avec la participation de Chanel, Fanta, Habiba, Issa et Shanys, élèves de quatrième (année scolaire 2021-2022) du collège Elsa Triolet (Paris) qui, semaine après semaine en séances « Devoirs faits », ont contribué à l'écriture du script et l'ont interprété sous la forme de ce petit sketch.

Dans une salle de classe de quatrième, un professeur et son groupe. Le professeur dialogue avec un élève au tableau.

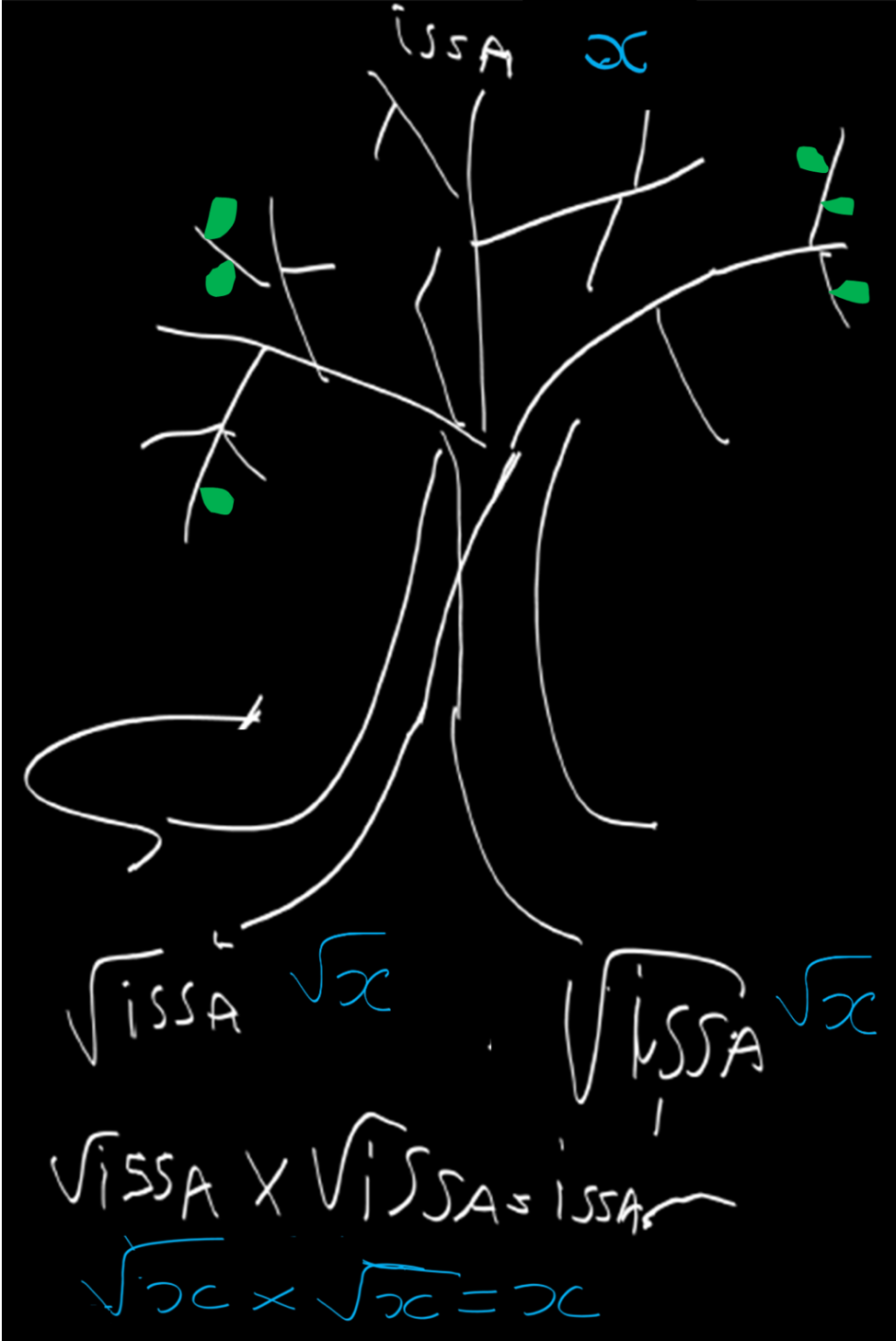
— Dessine-moi un arbre, Issa. Un bel arbre. L'élève regarde le professeur, étonné, puis dessine.

— Euh... je fais des feuilles aussi ?

— Si tu veux ; la jeunesse c'est le Printemps ; tu vas comprendre... Magnifique ! Vois-tu, cet arbre c'est toi. Inscris ton nom en haut : Issa.

— Issa ?

— Oui, toi, Issa... Très bien... Maintenant on va faire les racines. Comme tout le monde tu en as plutôt deux.

— Des racines ? Ah... Ahhh ! Mes parents ? Ma mère... Mon père, mes racines ! Le groupe s'amuse de sa découverte et rit avec lui.

— Oui ! C'est ça. Représente-les de la même taille : ils ont autant de valeur l'un que l'autre pour toi tes deux parents. À gauche, une racine de Issa. À droite l'autre racine de Issa.

— Avec... le symbole de la racine carrée ?

— Bien sûr ! Tu sais, il vient du « r » de « radix » (la « racine » en latin) qui a ensuite été stylisé ! Il y a toujours un commencement à tout, une racine, justement 1.  Le professeur montre comment la lettre s'est déformée tout en parlant.

— Ah, d'accord... À gauche $\sqrt{\text{Issa}}$, à droite aussi, $\sqrt{\text{Issa}}$.

— C'est ça. De là, tu fais monter deux lignes qui se croisent. Elles s'élèvent telles deux canaux de sève. En se multipliant, tes parents vont jusqu'à toi. Issa, tu es le produit de tes deux racines (figure 1).

—  ? 

— Issa, toi, tu es populaire.  L'élève sourit et rougit. Dans la classe de quatrième de ton collège. Si, tu es populaire, et timide. Et moi je sais qui tu es car je te vois toutes les semaines, chaque mercredi. Pense alors à l'élève illustre mais inconnu. En mathématiques, on le baptise $x$. De l'arabe « شيء » (prononcer « chay' », donnant le diminutif « chouya » en français) qui signifie « (quelque) chose ». L'initiale « ch » fut rendue phonétiquement par la lettre grecque $\chi$ au Moyen-Âge, laquelle a été miniaturisée en un petit $x$ ; du reste il sonne encore « ch » dans certaines langues régionales comme le basque. Le professeur trace les différents symboles au tableau ; il faut bien arrondir les jambes du $x$ pour ne pas le confondre avec la croix de la multiplication $\times$. Donc, pour ton camarade $x$ inconnu, tu changes de couleur. Mettons le bleu. Et tu reportes $x$ en haut.

— Et $\sqrt{x}$ en bas à gauche et en bas à droite.

— Exactement ! Résumons ; note, note : la racine carrée d'un premier nombre $x$, positif  (on n'a pas le choix), est le second, positif aussi (on aurait eu le choix) et noté $\sqrt{x}$ (ou $\sqrt[2]{x}$) qui, multiplié à lui-même, redonne le premier. Soit : $x = \sqrt{x} \times \sqrt{x}$, ou encore $x = (\sqrt{x})^2$. L'élève note, figure 2. Bon, suppose que $x$ joue le rôle de $4$ ; qui est $\sqrt{4}$ ?

— $2$.

— Oui !

— Et si $x$ est $36$ ?

— $18$.

— Non ! J'admets, le premier exemple était trompeur. Il ne faut pas répartir $36$ additivement, mais multiplicativement... Le professeur désigne du doigt le symbole de multiplication sur le tronc d'arbre.

— $6$ ?

— Oui !

— Et si $x$ est $49$ ?

— $7$.

— Bien !

— Et si $x$ est $48$ ?

— Entre les deux ?

— Lesquels deux ?

— $6$ et $7$.

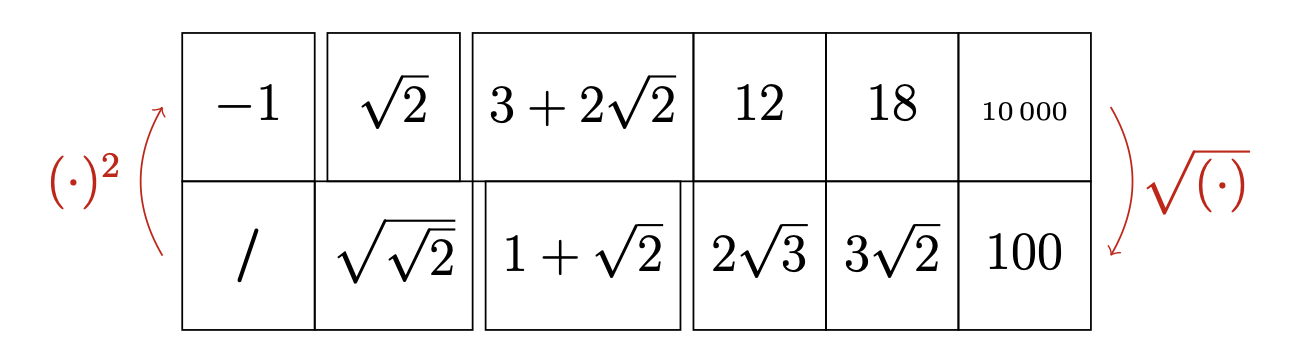
— Oui, plus proche de $7$ que de $6$, et on a besoin d'une virgule. Démonstration avec la calculatrice. D'ailleurs si tu arrondis ensuite : $6,9 \times 6,9$ renvoie presque $48$. Avec $6,92$ c'est encore plus précis. Etc.  Le professeur fait les opérations sur sa calculette puis fait remplir une table de correspondances, figures 3 et 4.

Habiba approche

— Moi j'ai grandi entre mon père, ma mère et ma sœur aînée : elle a aussi beaucoup compté quand j'étais petite.

— Tu as trois racines alors ?

— Oui. Rires de tout le monde.

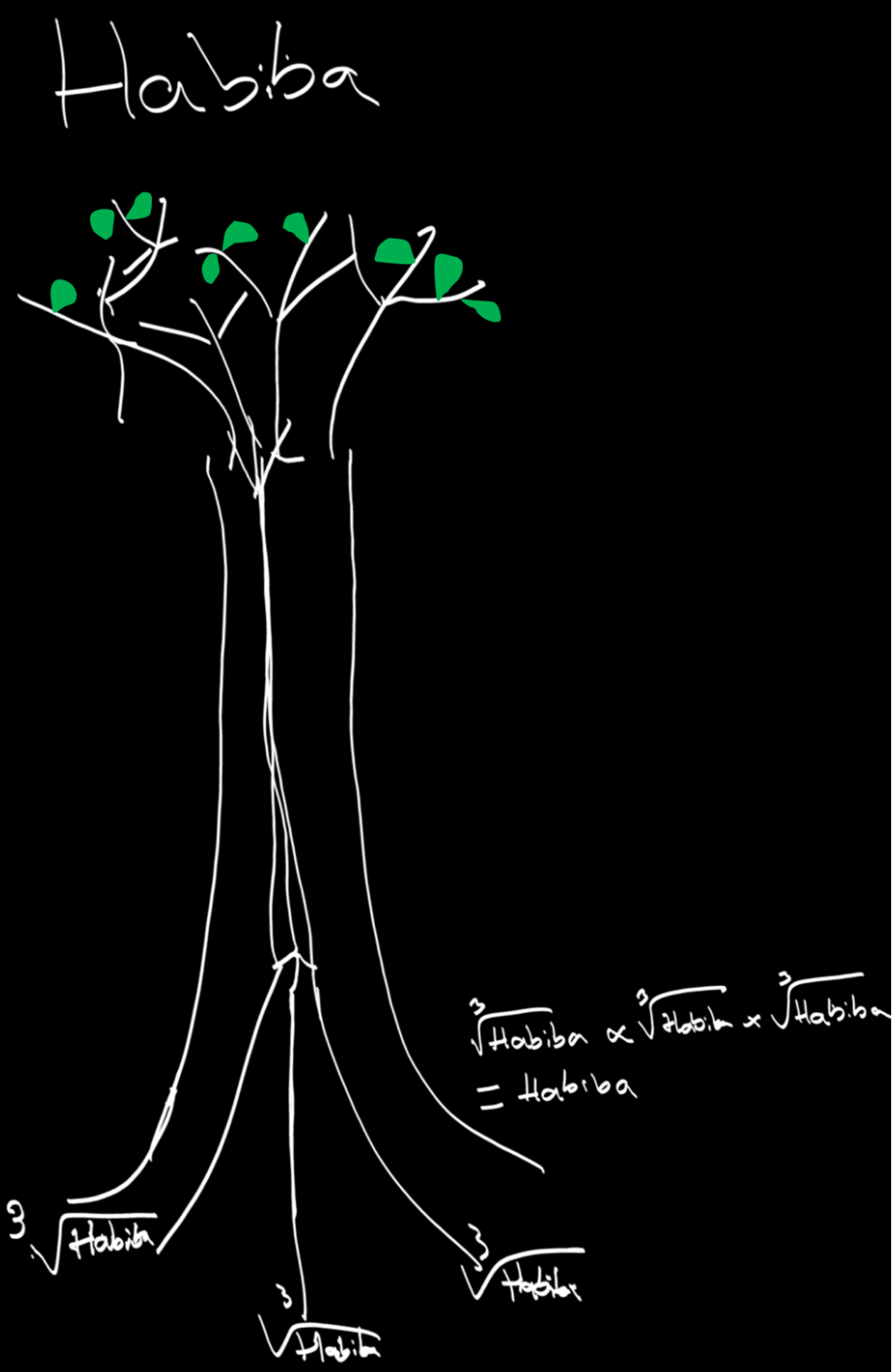
— On les appellera des racines cubiques. Vas-y, prends la craie et dis-nous. L'élève prend la craie.

— Et bien chaque racine vaut la racine cubique de Habiba.

— Yes ! Très bien. Elle s'écrit $\sqrt[3]{\text{Habiba}}$. Le professeur montre la notation au tableau.

— J'ai compris. Je suis le produit de mes trois racines. Ainsi $\text{Habiba} = \sqrt[3]{\text{Habiba}} \times \sqrt[3]{\text{Habiba}} \times \sqrt[3]{\text{Habiba}}$ (figure 5). Puis je change Habiba en $x$. Soit $x = \sqrt[3]{x} \times \sqrt[3]{x} \times \sqrt[3]{x}$ ou, en élevant au cube, $x = (\sqrt[3]{x})^3$. Puis je change $x$ en ce que je veux. Mettons $x=8$, qui donne $\sqrt[3]{8} = 2$

— Et non « $8$ divisé par $3$ », qui vaudrait $2,66$ et des poussières ; surtout pas hein !

— Ben non, évidemment, non ! Encore moins « $8$ au cube », qui vaudrait $8^3=512$.

— Parfait. Si $x=27$ ?

— $\sqrt[3]{27} = 3$.

— Oui ! Si $x = 64$ ?

— $\sqrt[3]{64} = 4$.

— Oui ! Si $x=60$ ?

— Ça tombe pas juste !

— Okay ! Au fait... Le professeur se tourne vers le groupe. Il y en a qui ont... cinq racines ici ? La classe rit de nouveau. Plusieurs s'exclament :

— Ben faudrait pas exagérer quand même M'sieur !

Fermeture au noir.

On retrouve les élèves quelques jours plus tard assis à leurs tables. Concentrés, ils résolvent des exercices. La caméra s'attarde sur les cahiers de Chanel, Shanys et Fanta qui construisent patiemment, arbre à calcul à l'appui, une spirale de Pythagore, dont les lignes (brisées) s'éloignent du centre des rayons $1$, $\sqrt{2}$, $\sqrt{3}$, $\sqrt{4}=2$, $\sqrt{5}$, etc.

Remerciements

Les auteurs remercient Carole Grigy, réalisatrice, pour ses conseils avisés ; Véronique Franzini, principale du collège Elsa Triolet (Paris), et Nora Machuré, proviseure de l'ENCPB — lycée Pierre-Gilles de Gennes (Paris), pour leur accueil chaleureux dans leurs établissements ; et Jean-Noël Bernard, professeur de spéciale à l'ENCPB — lycée Pierre-Gilles de Gennes (Paris), pour son assurance dans le maniement des tableaux tactiles.