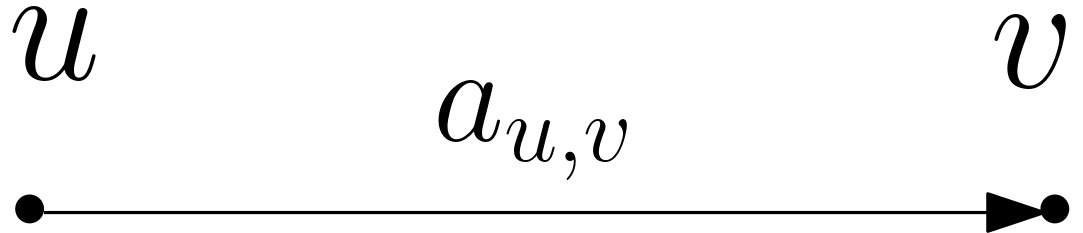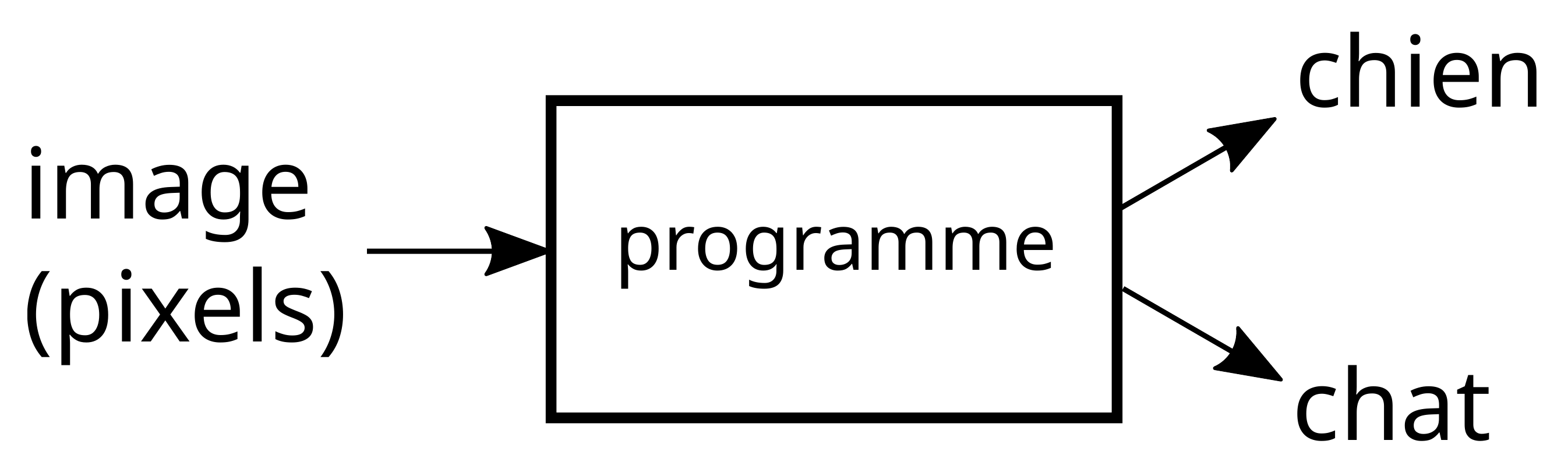
Commençons avec l’exemple d’un réseau de neurones, comme ceux qui ont ces dernières années permis à la reconnaissance d’images de faire de grands progrès. Un exemple pédagogique classique dans ce domaine consiste à vouloir distinguer les photos de chiens des photos de chats. On souhaite donc avoir un programme informatique qui, sur la donnée des pixels d’une image, répond « chien » ou « chat », comme dans la figure 1.

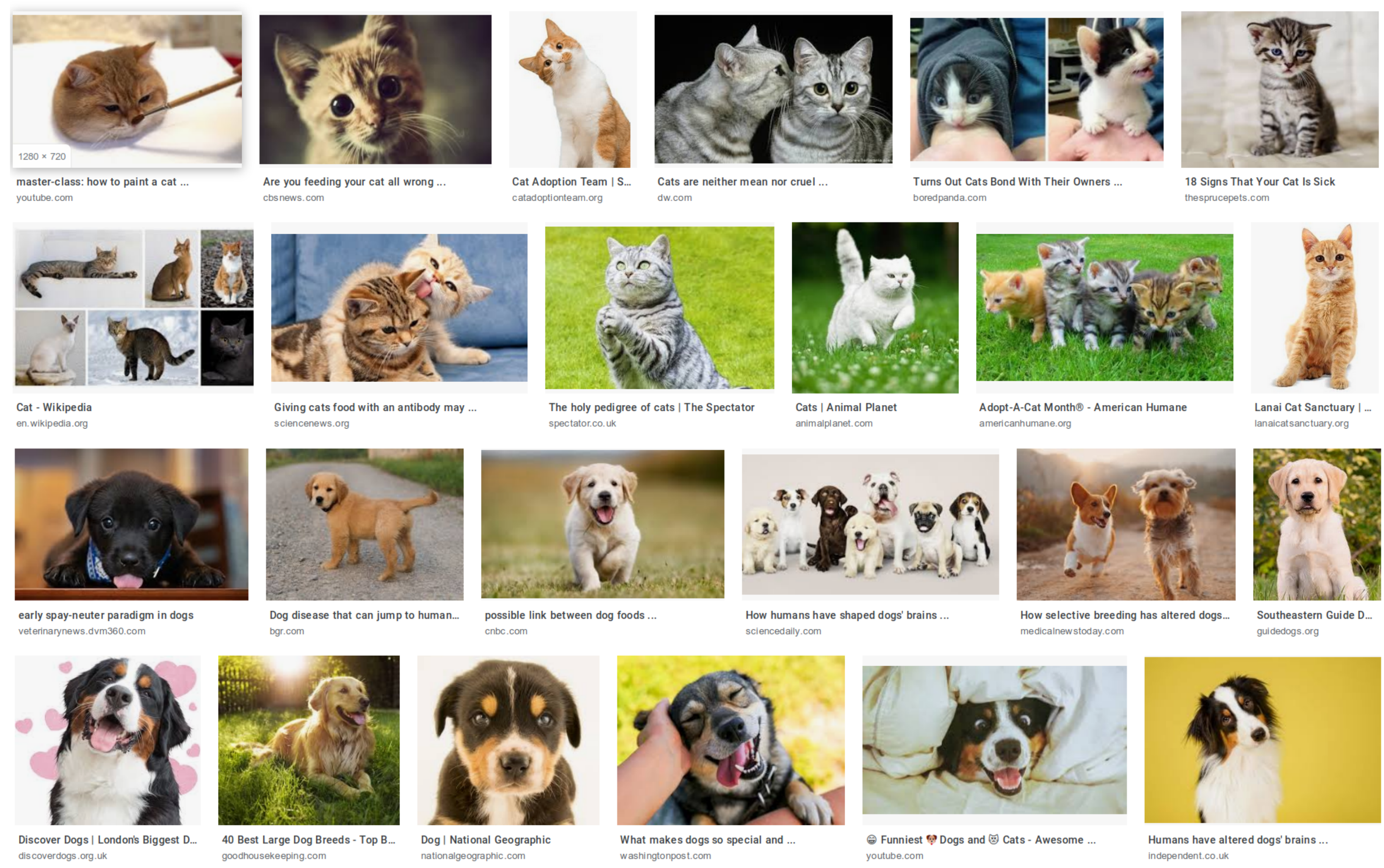
On accepte d’ailleurs que le programme se trompe de temps en temps, comme d’ailleurs un humain pourrait se tromper. C’est un problème difficile pour la programmation classique, car la photo peut varier dans son éclairage, son angle, sa distance, son contexte, et aussi car il existe de nombreuses espèces différentes de chiens et de chats, comme le montre par exemple la figure 2. Une bonne façon de se rendre compte de cette difficulté est de s’imaginer expliquer verbalement à un extraterrestre comment distinguer un chat d’un chien, sans pouvoir montrer d’exemples.

Les réseaux de neurones, et l’apprentissage machine en général, prennent une approche différente. Le programme est remplacé par un modèle avec des paramètres. Nous pouvons représenter cela par la figure 3.

Cela ne semble pas être un grand changement par rapport au cas précédent, mais il faut imaginer maintenant le modèle comme une machine fixée une fois pour toutes et les paramètres comme des boutons permettant de régler la machine. Cette machine peut être plus ou moins bien réglée, selon la valeur qu’on donne aux paramètres. Pour certaines valeurs le modèle donnera souvent la bonne réponse, c’est-à-dire pour beaucoup d’images, tandis que pour d’autres il se trompera souvent. Nous avons donc remplacé la recherche d’un programme qui puisse résoudre notre problème par celle de valeurs numériques à donner à des paramètres. Notons au passage qu’il n’est pas sûr que nous puissions trouver de telles bonnes valeurs : nous n’avons peut-être pas acheté la bonne machine et il n’y a pas alors de réglage satisfaisant. Nous ne considérerons pas ici le problème du choix de la machine, mais uniquement celui de la recherche d’un bon réglage pour une machine donnée.

C’est ici que la méthode se rapproche de ce que l’on ferait naturellement, mais que nous avions interdit auparavant : montrer des photos à quelqu’un pour lui expliquer comment distinguer un chat d’un chien. Probablement même beaucoup de photos et en lui disant à chaque fois « voici un chien » ou « c’est un chat ». Nous allons faire de même avec notre machine. Nous avons donc un ensemble d’images fixé, avec à chaque fois la réponse associée, et nous cherchons de bonnes valeurs à donner aux paramètres pour que le modèle donne souvent la bonne réponse. On espère qu’avec les valeurs de paramètres ainsi obtenues il donnera la bonne réponse assez souvent même sur de nouvelles images. On parle d’apprentissage machine supervisé, où le modèle a besoin d’être entraîné.

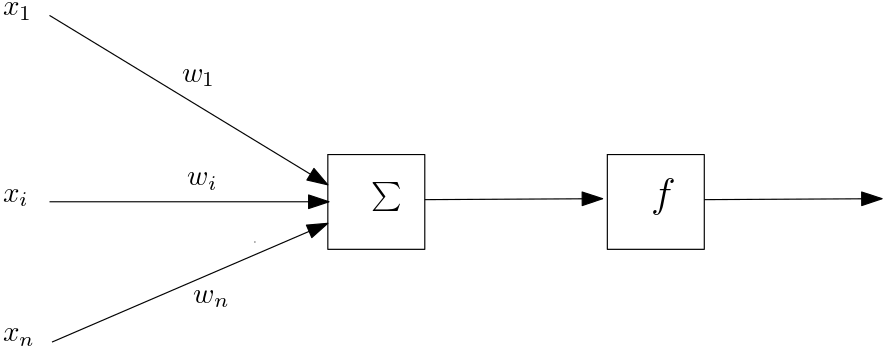
Précisons donc le cas où le modèle choisi est un réseau de neurones. Le nom indique une inspiration biologique, mais c’est un modèle de calcul dont la description abstraite est très simple. Un « neurone » ici reçoit en entrée des valeurs et applique une certaine fonction pour calculer une valeur de sortie. Sur la figure 4, on voit ainsi un neurone comme prenant des valeurs \(x_1,\dots,x_n\) en entrée, multipliant chaque \(x_i\) par un poids \(w_i\), sommant toutes ces valeurs avant d’appliquer une fonction \(f\). Si cette dernière est une fonction de type « seuil », notre neurone fait donc une somme pondérée des signaux qu’il reçoit et teste si celle-ci dépasse un certain seuil pour s’activer, comme pour un neurone biologique. Mais rien ne nous force à utiliser une telle fonction.

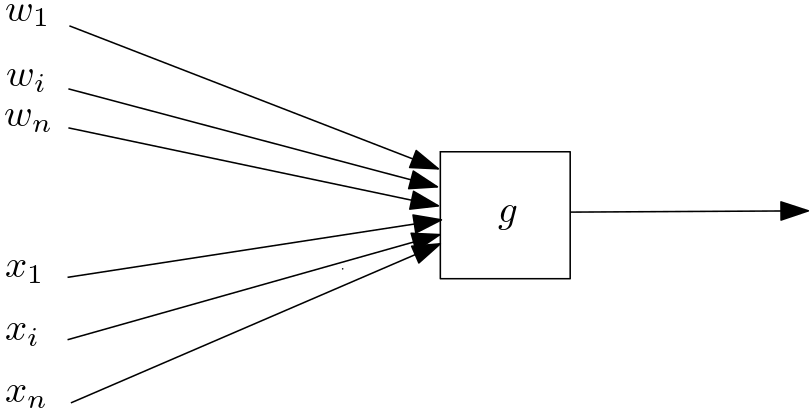
Pour cet article, nous préférerons donc rester plus abstraits et voir chaque neurone comme appliquant une opération \(g\) à ses entrées, opération utilisant aussi un certain nombre de paramètres \(w_i\), comme illustré sur la figure 5.

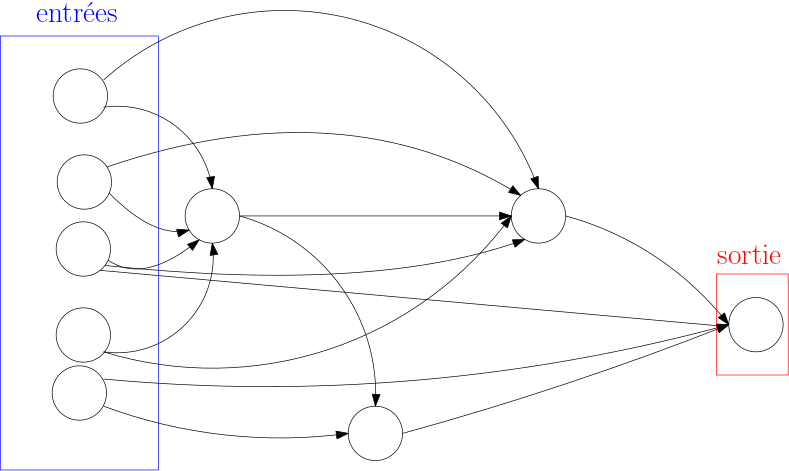
Si nous reprenons l’inspiration biologique, les neurones sont connectés entre eux et la sortie de l’un va influencer l’activation d’un autre. Dans un réseau de neurones artificiel, nous allons retrouver une structure similaire. La figure 6 en montre un exemple, avec :

• des neurones d’entrée, qui prendront les valeurs sur lesquelles on souhaite faire calculer notre réseau ;

• des neurones intermédiaires ;

• un neurone de sortie, qui prendra comme valeur le résultat du calcul du réseau (notons qu’il pourrait y avoir plusieurs neurones de sortie, mais un seul suffira dans notre cas).

Le calcul se propage dans le réseau de manière intuitive : si on met dans les neurones d’entrée des valeurs, on peut ensuite calculer les valeurs prises par les neurones qui en recoivent des flèches, puis les suivants, et ainsi de suite jusqu’au neurone de sortie.1 Dans le cas qui nous intéresse, les neurones d’entrée prendront comme valeurs les pixels d’une image.

Comme nous l’avons vu, chaque neurone de notre réseau peut faire intervenir des paramètres, si bien que le fonctionnement global dépend de l’ensemble \(\theta\) des paramètres de tous les neurones. C’est donc ces paramètres que l’on cherche à fixer pour que le réseau donne le plus souvent possible la bonne réponse.

Cela se fait lors de la phase d’entraînement qui, comme nous l’avons dit, repose sur un ensemble d’images pour lesquelles nous connaissons la réponse. Nous pourrions par exemple utiliser celui de Kaggle, qui contient \(25000\) images. Soyons plus précis en introduisant un peu de notation qui nous servira par la suite. Nous avons un ensemble de couples \((I_k,O_k)\), pour \(1\leq k\leq N\), où :

• \(I_k\) est une image, de chien ou de chat, que nous voyons comme des valeurs à donner aux entrées du réseau de neurones ;

• \(O_k\) est la valeur attendue en sortie, disons \(1\) pour un chat et \(0\) pour un chien.

Il nous faut d’abord définir une fonction mesurant la performance du réseau, c’est-à-dire un score numérique obtenu en comparant les réponses (chien ! chat !) qu’il a fournies avec celles qui étaient attendues. Pour cela, nous allons supposer que notre réseau renvoie en sortie son degré de confiance que l’image en entrée était un chat : \(1\) s’il est complètement sûr que c’est un chat, \(0\) s’il est sûr que c’est un chien, et des valeurs intermédiaires selon son degré de certitude. Pour une image \(I_k\) de notre ensemble d’entraînement et une réponse \(R_k\) du réseau, définissons une mesure \(L_k\) de l’erreur du réseau sur cette image par \(L_k = (O_k - R_k)^2\). Si \(I_k\) est une image de chat, alors \(O_k\) vaut \(1\) et \(L_k\) sera d’autant plus petite que \(R_k\) est proche de \(1\), c’est-à-dire si le réseau pense fortement que c’est un chat. Par exemple, si le réseau est sûr à \(90\%\) que c’est un chat, alors \(R_k\) vaut \(0.9\) et \(L_k\) vaut \(0.01\). Par contre si le réseau pense à \(80\%\) que c’est un chien, donc à \(20\%\) que c’est un chat, alors \(R_k\) vaut \(0.2\) et \(L_k\) vaut \(0.64\). De même, si \(I_k\) est une image de chien, \(L_k\) sera d’autant plus petite que \(R_k\) est proche de \(0\). \(L_k\) semble donc bien mesurer l’erreur que fait le réseau sur la \(k\)-ième image. Une mesure naturelle pour l’erreur sur les \(N\) images de l’ensemble d’entraînement est \(L = \sum_{k=1}^{N} L_k\). (On pourrait aussi diviser par \(N\) pour moyenner, cela ne change rien pour notre discussion.) La recherche d’une bonne valeur à donner aux paramètres \(\theta\) est alors un problème de minimisation de cette fonction \(L\) par rapport à \(\theta\).

Optimisons !

Chaque valeur donnée aux paramètres nous donne une valeur de l’erreur. Chaque paramètre est comme un potentiomètre que l’on peut tourner pour voir si cela améliore le résultat final. Notre réseau de neurones ressemble un peu à l’interconnexion de nombreux effets de guitare, comme sur la figure 7. Comment se rapprocher du son que l’on souhaite, si ce n’est en tournant les boutons un peu au hasard ?

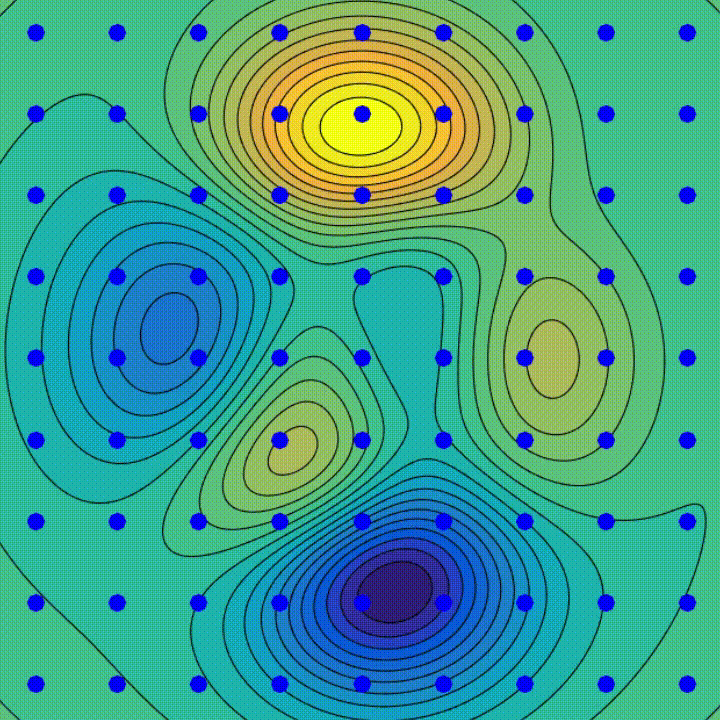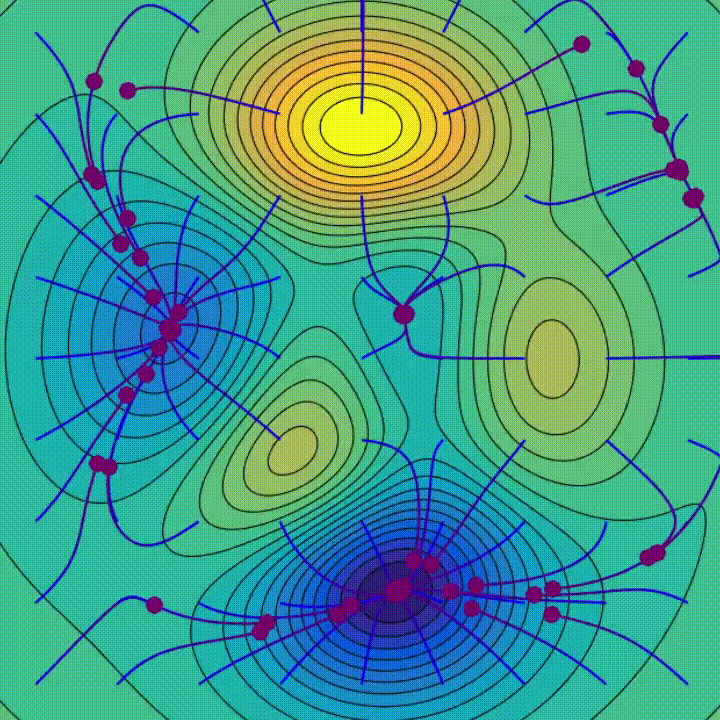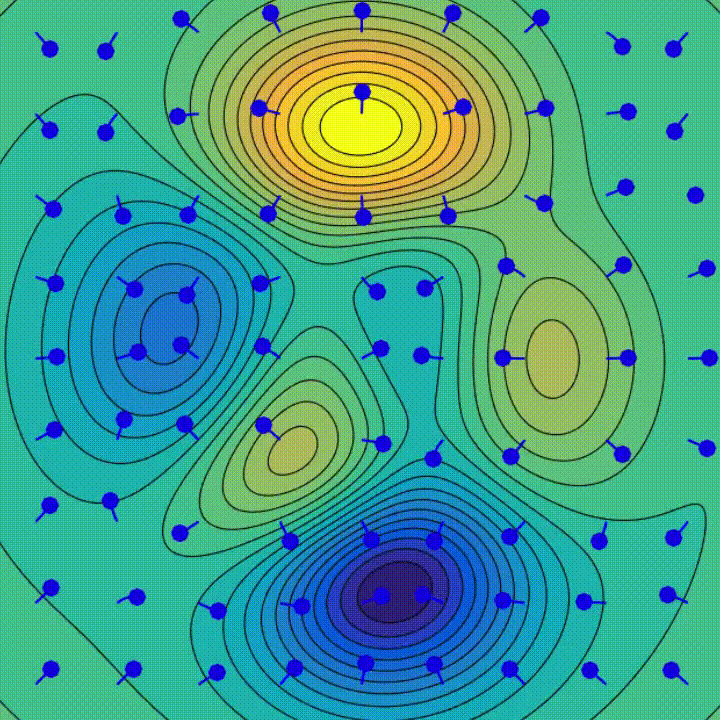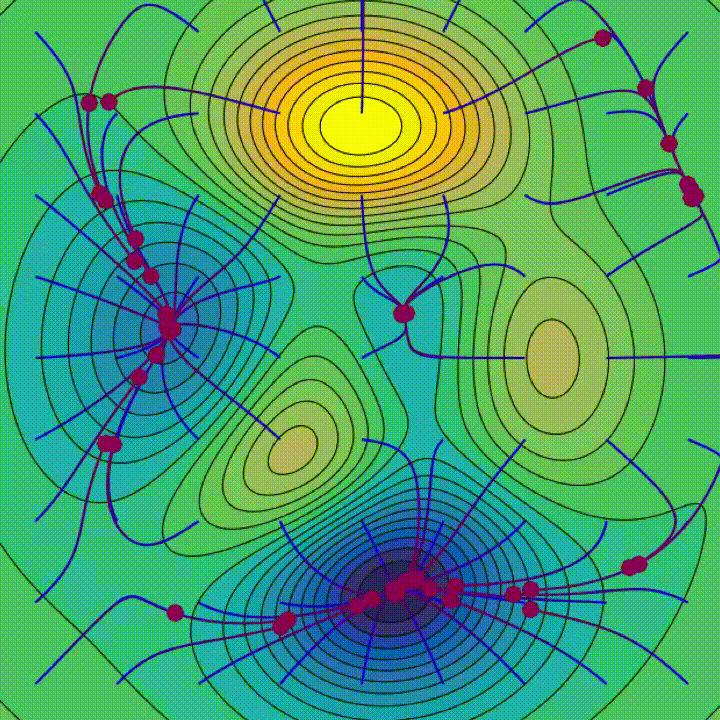
Pour notre problème nous avons des stratégies plus efficaces, sous certaines conditions sur la fonction \(L\) que nous supposerons vraies ici. La minimisation consiste souvent, à partir d’un point de départ, à se déplacer sur la « surface » de la fonction en essayant de trouver un minimum. En particulier, parmi les différentes techniques d’optimisation, on utilise souvent pour les réseaux de neurones la descente de gradient. Il s’agit de se déplacer dans le sens opposé du gradient de la surface d’erreur au point actuel, ce qui correspond à descendre dans la direction de la plus grande pente, en espérant ainsi atteindre un minimum global ou un minimum local suffisamment bon (on voit les trajectoires obtenus selon le point de départ sur l'animation de la figure 8). Cette description simple cache de nombreuses difficultés techniques, surtout dans le cas de réseaux modernes dont le nombre de paramètres peut atteindre facilement plusieurs millions, néanmoins il indique bien l’ingrédient indispensable : le calcul du gradient, c’est-à-dire des dérivées partielles de \(L\) par rapport à chacun des paramètres.

La complexité du réseau empêche d’espérer utiliser un calcul symbolique des dérivées partielles qu’il resterait alors seulement à évaluer. Il s’agira donc d’un calcul numérique. Revenons à notre fonction \(L = \sum_{k=1}^{N} L_k\). La dérivation est une opération linéaire, ce qui veut dire que la dérivée de la somme est la somme des dérivées. Nous commençons donc par nous concentrer sur une seule fonction \(L_k\), mesurant l’erreur sur la \(k\)-ième image, et le calcul de ses dérivées partielles.

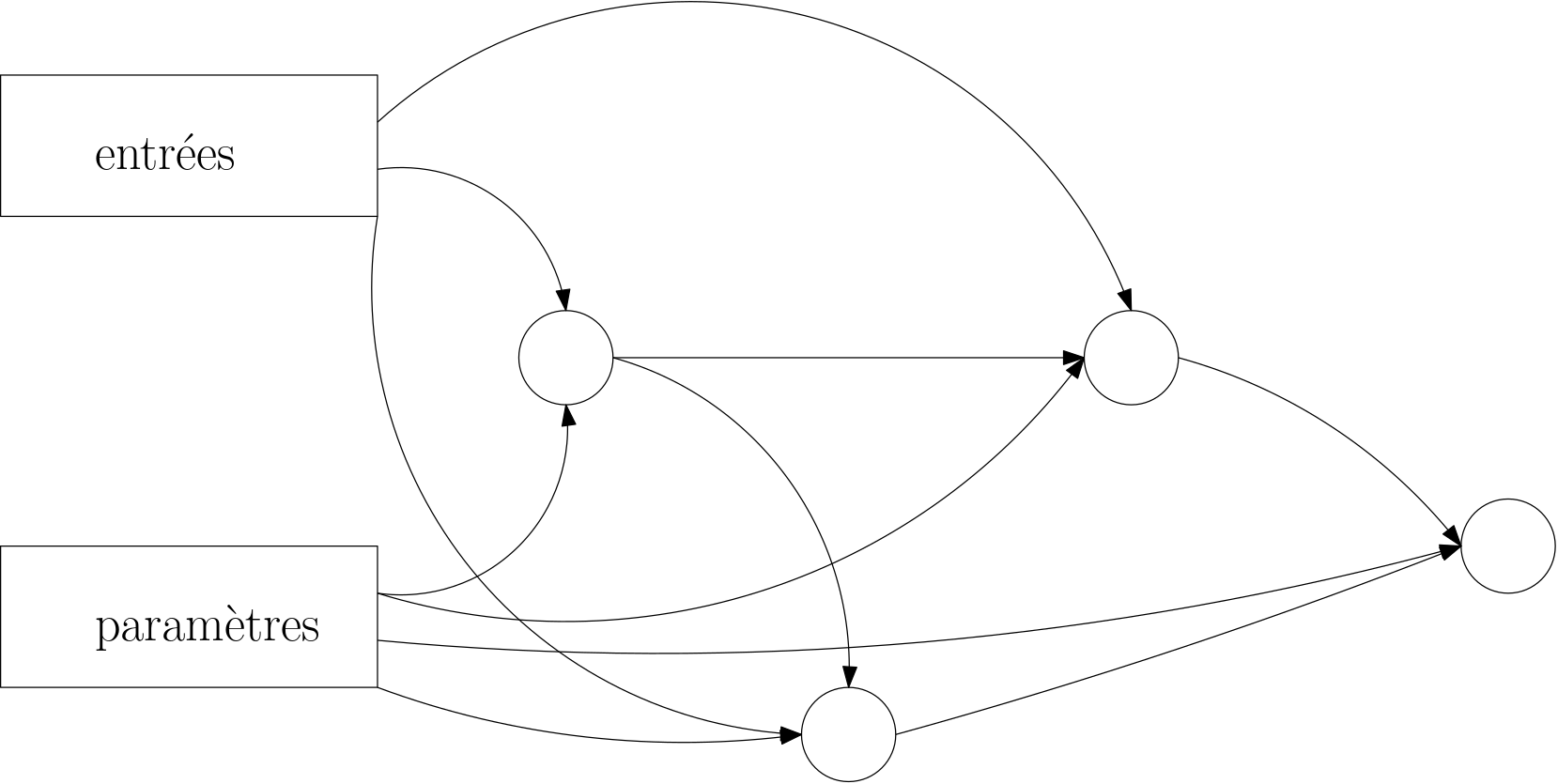
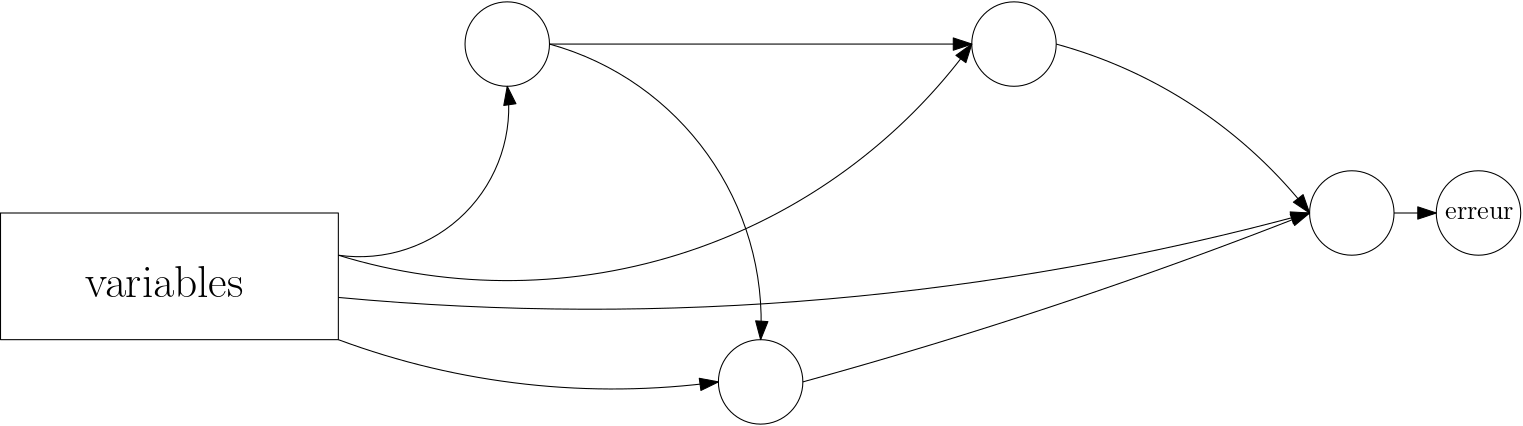
Supposons que la figure 9 représente notre réseau. Pour l’image \(I_k\) fixée, la sortie ne dépend que des paramètres. Nous pouvons y ajouter une étape de calcul évaluant l’erreur et considérer que les entrées (l’image \(I_k\), fixée donc) sont codées « en dur » dans le réseau. La sortie ne dépend alors plus que des paramètres. Nous obtenons ainsi la figure 10, où nous appelons désormais les paramètres des variables, pour nous rapprocher du langage mathématique : les paramètres de notre réseau sont donc les variables dont dépend la fonction \(L_k\).

Notre problème d’optimisation s’est donc réduit, via la descente de gradient, à itérer une procédure où nous avons besoin de calculer toutes les dérivées partielles d’une fonction par rapport à ses variables, sachant que la fonction est donnée sous la forme d’un réseau de neurones.

Encore plus simple : les circuits arithmétiques

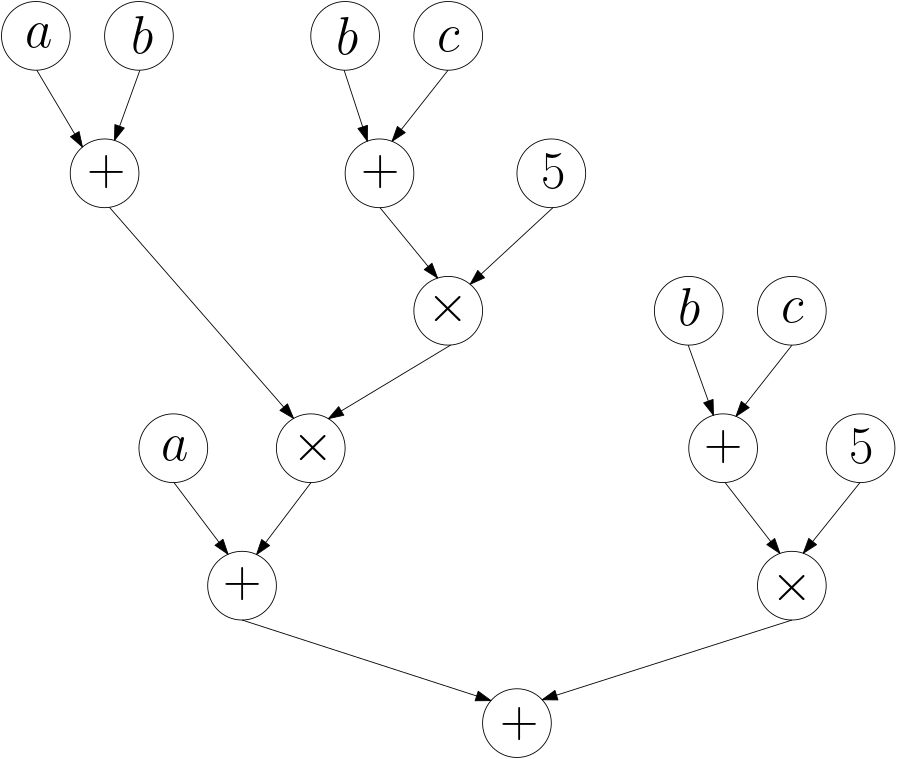
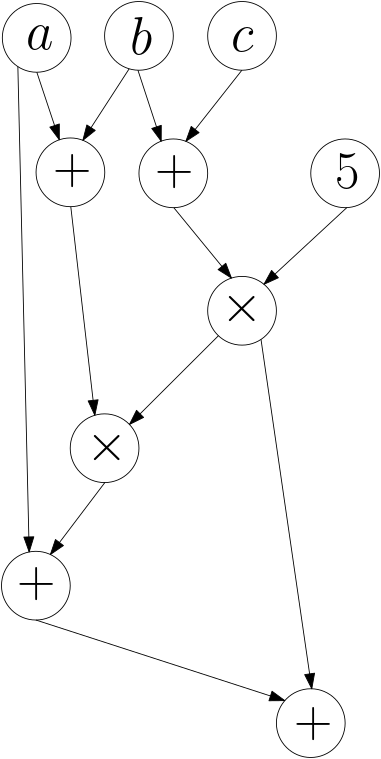
Faisons un petit détour et laissons pour l’instant notre problème d’optimisation. Considérons d’abord une expression arithmétique, comme par exemple \((a + ((a+b)*((b+c) * 5)))+((b+c) * 5)\). Le parenthésage de cette expression arithmétique définit une structure d’arbre, et il est clair qu’on peut représenter cette expression, sans les parenthèses, sous la forme de la figure 11.

On remarque alors qu’on pourrait vouloir éviter d’écrire deux fois (et donc de calculer deux fois) la partie \(((b+c) * 5)\), et on obtient alors la figure 12.

La ressemblance avec la figure du réseau de neurones est immédiate : il s’agit finalement du même genre d’objet, sauf que les opérations éventuellement complexes réalisées dans les neurones sont maintenant les simples opérations arithmétiques. Finalement, dans les deux cas, nous avons un graphe de calcul, c’est-à-dire un ensemble de sommets représentant des « petits » calculs locaux et des flèches indiquant la propagation des valeurs calculées, des variables en entrée jusqu’à la sortie. Même s’il existe aussi une terminologie propre aux circuits arithmétiques, nous allons par la suite donc utiliser celle des graphes. Dans cette partie, notre graphe de calcul est un circuit arithmétique et les sommets peuvent alors être : une variable ou une constante (ce sont les entrées), une addition, ou une multiplication. Il y a un sommet de sortie où, une fois le calcul propagé pour certaines valeurs des variables des sommets d’entrée, on aura la valeur calculée par le circuit.

Nous pouvons donc nous poser le même problème, plus simple peut-être à visualiser : étant donné un circuit arithmétique calculant une fonction \(f\), comment calculer toutes les dérivées partielles de \(f\) par rapport à ses variables ? Nous allons décrire une méthode dans le cas des circuits arithmétiques, mais elle s’appliquera aux réseaux de neurones et, plus généralement, à tout graphe de calcul.

On connaît les règles de dérivation du produit et de la somme. Pour une variable donnée, par exemple \(a\) dans notre circuit, il est donc facile de modifier ce dernier pour qu’il calcule aussi \(\tfrac{\partial f}{\partial a}\). Nous en donnons une description sommaire ici, mais la compréhension de cette procédure n’est pas nécessaire pour la suite. La construction se fait de proche en proche pour tous les sommets du circuit. La dérivée d’un sommet avec une variable distincte de \(a\) ou une constante prend la valeur \(0\), car sa dérivée partielle par rapport à \(a\) est nulle. La dérivée d’un sommet avec la variable \(a\) prend la valeur \(1\). Pour un sommet d’addition, comme on a déjà des sommets calculant les dérivées partielles de ses deux arguments, il suffit d’additionner ceux-ci, car la dérivée d’une somme est la somme des dérivées ; pour un sommet de multiplication il faut appliquer le fait que \(\tfrac{\partial uv}{\partial a} = u \tfrac{\partial v}{\partial a} + \tfrac{\partial u}{\partial a} v\), ce qui ajoute \(3\) sommets. Au total le nombre de sommets du circuit est multiplié au plus par \(4\).

Mais si on veut toutes les dérivées partielles, et si on a \(n\) variables dans notre circuit, la méthode du paragraphe précédent multiplie la taille du circuit (son nombre de sommets) par \(4n\). Dans le cas de réseau de neurones modernes, \(n\) peut être de l’ordre du million, ce qui implique une trop grosse augmentation de la taille. Peut-on faire mieux ?

À la chaîne

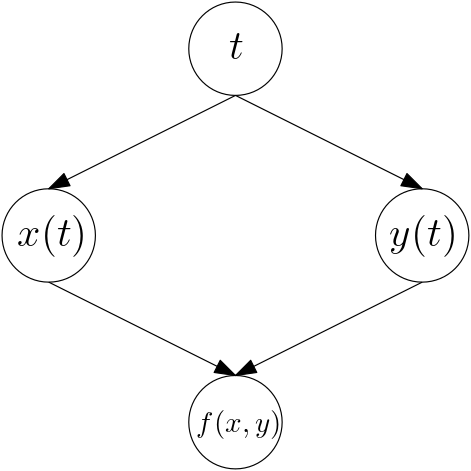
Nous allons essayer d’utiliser une connaissance locale sur le cours du calcul pour obtenir d’un coup nos dérivées partielles. Nous savons tous calculer la dérivée d’une composée : \((f \circ g)' = (f' \circ g) \cdot g'\). Cette relation s’appelle souvent « chain rule » en anglais et c’est cet enchaînement qui nous intéresse. En effet, dans un circuit, nous enchaînons de nombreuses opérations élémentaires et ce que nous voulons c’est la dérivée de la composée. Dans le cas de fonctions de plusieurs variables, on l’écrit un peu différemment. Par exemple, pour une fonction \(f(x,y)\), où \(x\) et \(y\) dépendent de \(t\), on aura : \(\frac{\partial f}{\partial t} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t}\).

Représentons cela sur un dessin : sur la figure 13, nous avons des sommets pour \(t\), puis pour \(x\), \(y\) et enfin pour \(f\). Ajoutons alors sur les flèches entre ces sommets les dérivées partielles « locales » : par exemple, la flèche allant du sommet calculant \(x\) à celui calculant \(f\) est étiquetée par \(\tfrac{\partial f}{\partial x}\) : cela donne la figure 14.

Nous voyons que la dérivée partielle souhaitée consiste à suivre les chemins allant du sommet \(t\) au sommet \(f\). Sur chaque chemin on multiplie les étiquettes rencontrées sur les flèches, puis on additionne.

En particulier, dans le cas d’un circuit arithmétique, cette information locale à affecter aux flèches est très simple, comme le montre la figure 15. Pour un sommet faisant l’addition de deux autres sommets, les flèches ont juste l’étiquette \(1\), car \(\tfrac{\partial (u + v)}{\partial u} = 1\). Pour un sommet de multiplication \(w\), calculant le produit de deux sommets \(u\) et \(v\), alors la flèche de \(u\) à \(w\) se verra affecter l’étiquette \(v\), car \(\tfrac{\partial (uv)}{\partial u} = v\). On voit que les valeurs calculées par les sommets du circuit seront a priori nécessaires pour pouvoir étiqueter les arêtes, et donc pour la suite de notre calcul : dans le cas des réseaux de neurones, il s’agit de la partie parfois appelée « forward propagation ».

Revenons à notre « chain rule » vue sur les circuits. Pour un chemin entre deux sommets, le poids du chemin est le produit des étiquettes des flèches composant le chemin. Alors on peut montrer qu’en général, si on considère deux sommets \(a\) et \(b\) dans le circuit, la dérivée partielle de \(b\) par rapport à \(a\) est la somme des poids des chemins de \(a\) à \(b\). C’est de cette façon que l’information locale des dérivées partielles des sommets pourra être accumulée pour le calcul des dérivées partielles de la fonction qui nous intéresse, à la sortie du circuit.

Beaucoup de chemins

Notre question d’optimisation a encore évolué. Nous sommes ainsi ramenés à des questions de calcul de sommes de poids de chemins dans un graphe avec des étiquettes sur les flèches. Pour toute flèche d’un sommet \(u\) à un sommet \(v\) du graphe, notons \(a_{u,v}\) son étiquette. Fixons un sommet \(u\) dans ce graphe. Si \(v\) est un sommet recevant une flèche de \(u\) et tel qu’il n’y a pas d’autre chemin de \(u\) à \(v\), il est facile de calculer la somme des poids des chemins de \(u\) à \(v\) : c’est tout simplement \(a_{u,v}\) (voir figure 16).

On peut procéder ainsi de proche en proche, en suivant un ordre sur les sommets impliquant qu’on ne considère pas un sommet avant d’avoir traité tous ceux dont il reçoit des flèches. Cet ordre est rendu possible par le caractère acyclique du graphe, lui-même provenant ici du fait que nous sommes partis de circuits arithmétiques (ou de réseaux de neurones) sans boucle de feedback.

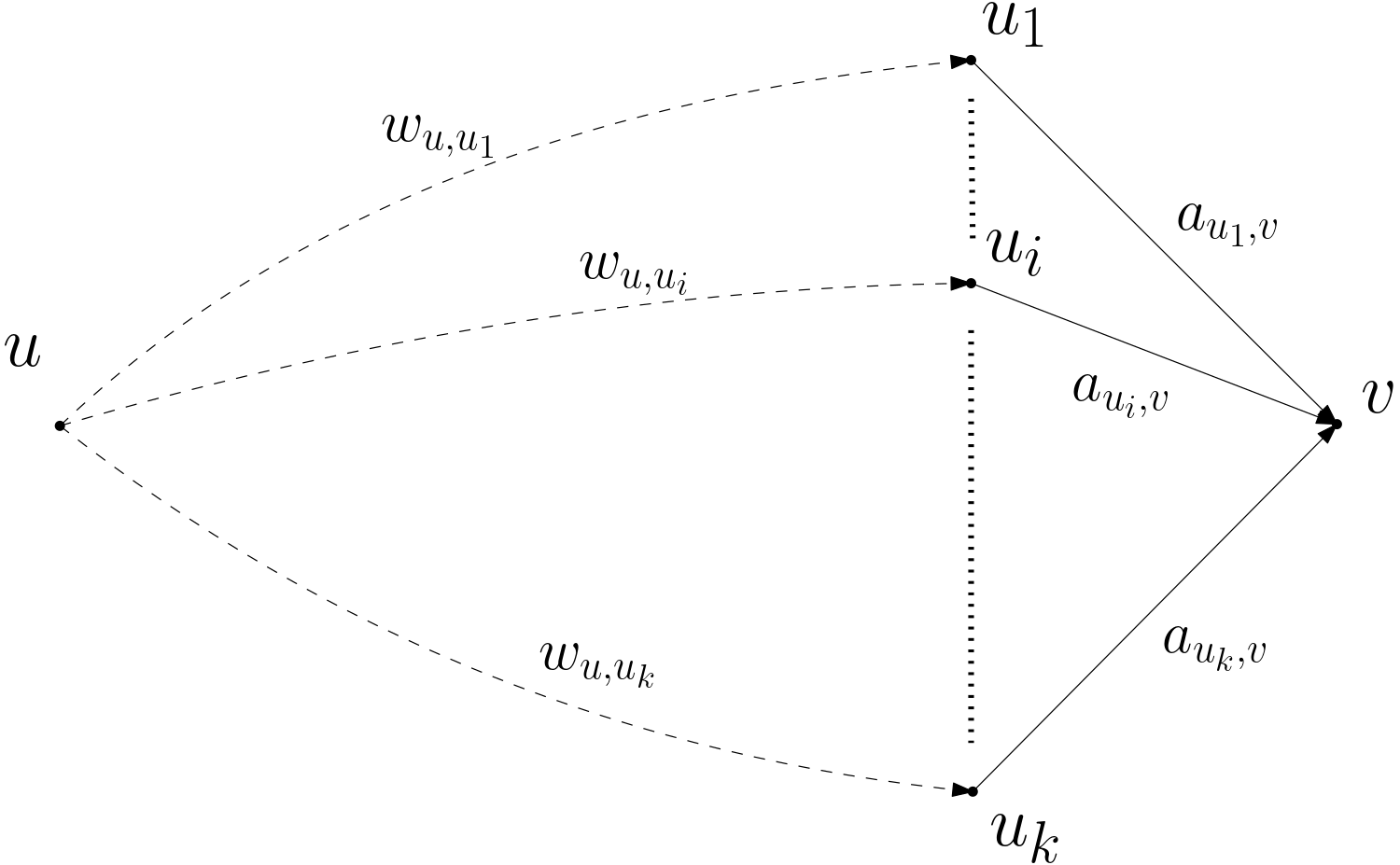
Pour deux sommets \(u, v\), appelons \(W_{u, v}\) la somme des poids des chemins de \(u\) à \(v\). Soit maintenant \(v\) un sommet recevant des flèches des sommets \(u_1,\dots,u_k\) (figure 17), alors \(W_{u,v} = \sum_{i=1}^{k} W_{u,u_i} \cdot a_{u_i,v}\). Le calcul se propage donc ainsi. Si on le poursuit jusqu’au bout, on a alors, à partir de notre sommet \(u\) fixé et pour chaque sommet \(v\), la somme des poids des chemins de \(u\) à \(v\).

Rembobinons

En revenant à notre interprétation, si \(u\) correspond à un sommet d’entrée du circuit, donc à une variable \(a\), ce calcul nous donne alors les valeurs des dérivées partielles \(\tfrac{\partial g}{\partial a}\) pour toutes les fonctions \(g\) calculées par les sommets du circuit. Mais ce n’est pas ce qui nous intéresse ! Nous voulons les dérivées partielles, seulement du sommet de sortie, mais par rapport à toutes les variables. Autrement dit, dans le graphe, nous voulons fixer le sommet d’arrivée \(w\), pour qu’il corresponde à la sortie, et calculer pour chaque sommet \(u\) du graphe la somme des poids des chemins de \(u\) à \(w\). Il s’agit alors du même procédé mais à l’envers. C’est le rétro dans rétropropagation. En faisant un petit effort d’imagination, on voit qu’on aura de nouveau un calcul étape par étape, en partant de \(w\).

En supposant les dérivées partielles locales connues, nous voyons que ce procédé nécessite un nombre d’étapes proportionnel au nombre de flèches du graphe. Or si le graphe provient d’un circuit arithmétique, ce nombre est lui-même proportionnel au nombre de sommets (puisqu’un sommet de calcul reçoit au plus deux flèches). Au lieu d’un calcul où la taille du circuit était multipliée par un facteur linéaire en le nombre de variables par rapport auxquelles on dérive, comme dans notre première stratégie naïve, nous avons ici un calcul qui multiplie simplement la taille par une constante.

Repensons à notre réseau de neurones et à ses millions de paramètres potentiels et nous pouvons imaginer le gain. D’autant plus que le calcul dans la phase d’entraînement devait être répété pour chaque exemple, puis tout cela répété après modification des paramètres par la méthode de descente de gradient. D’ailleurs certaines variantes de la méthode tirent à chaque étape un petit nombre d’exemples au hasard pour évaluer le gradient, perdant en précision pour gagner en temps de calcul (on appelle cela stochastic gradient descent). Nous avons donc apporté une solution raisonnable à notre problème d’optimisation et donc à l’entraînement de notre réseau de neurones. Revenons un peu aux circuits arithmétiques pour voir ce que notre capacité à calculer des dérivées efficacement peut nous apprendre.

Y a-t-il vraiment des problèmes durs ?

Éloignons-nous donc un peu des questions de chiens et de chats. Les ordinateurs calculent vite. Mais parfois ce n’est pas assez rapide : on attend un peu pour le traitement d’une image, ou un jeu vidéo n’est pas assez fluide... Il y a donc des problèmes qu’un ordinateur peut résoudre rapidement et d’autres où il lui faut plus de temps. En informatique théorique, on essaie donc de classifier les problèmes selon leur difficulté pour un ordinateur. Dire ici « pour un ordinateur » peut prêter à confusion : un ordinateur peut résoudre rapidement un problème si quelqu’un a trouvé une façon de le résoudre (un algorithme) qui ne nécessite pas beaucoup de calculs une fois programmée pour l’ordinateur. C’est donc une question qui ne dépend pas seulement des ordinateurs mais de nous. Donc si on a trouvé une telle méthode pour un problème donné, on sait qu’il est facile et on a classifié le problème. Mais si personne n’a trouvé de bonne méthode, on ne peut pas directement en déduire que le problème est difficile : peut-être existe-t-il un algorithme rapide, mais on ne l’a pas trouvé pour l’instant.

De ceci découle l’une des questions ouvertes majeures de l’informatique et des mathématiques : savoir si de nombreux problèmes a priori difficiles à résoudre pour un ordinateur (mais dont on sait facilement vérifier une solution si on nous en propose une) seraient en fait faciles à résoudre (i.e., en temps polynomial en la taille de l’entrée), ou non. On appelle NP le premier ensemble de problèmes et P le second et on aimerait alors savoir si P est égal à NP. Prenons un exemple. Sur la donnée d’une carte avec des villes reliées par des routes, il est par exemple facile de vérifier si un parcours qu’on nous propose passe exactement une fois par chaque ville. Mais nous ne connaissons pas de méthode rapide pour déterminer, sur la donnée d’une carte, si un tel parcours existe : c’est un problème NP et on ne sait pas s’il est dans P. L’importance de la question P \(=\)? NP, ouverte depuis \(50\) ans, est pratique en plus d’être théorique, par exemple car certains problèmes réputés difficiles sont à la base de techniques cryptographiques. C’est aussi un des Millenium problems du Clay Mathematics Institute, avec un prix d’un million de dollars en récompense.

Il existe une version de cette question qui s’exprime en termes de circuits arithmétiques, ceux que nous avons vus auparavant, et des polynômes (en plusieurs variables) qu’ils calculent. On parle alors de la question VP \(=\)? VNP. Pour les besoins de cet article il suffira de penser que VP correspond aux polynômes rapides à calculer et VNP à ceux qu’on peut décrire facilement, mais dont on ne connaît pas de calcul rapide. Voici néanmoins une définition un peu plus précise, qu’il n’est pas nécessaire de comprendre pour la suite : VP est l’ensemble des polynômes calculables par un circuit arithmétique de taille polynomiale en le nombre de variables, tandis que VNP est intuitivement l’ensemble des polynômes dont on peut calculer rapidement les coefficients. Un peu de travail permet de montrer que la question VP \(=\)? VNP se résume à peu près à la comparaison entre deux polynômes fondamentaux.

Le premier polynôme est le déterminant. Son expression formelle pour une matrice \((x_{i,j})_{1\leq i,j \leq n}\) est : \[\sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^{n} x_{i,\sigma(i)},\] où \(S_n\) est le groupe des permutations de \(\{1,\dots,n\}\) et la fonction \(\text{sgn}\) donne la signature de la permutation.1 Une façon de le calculer est de faire des opérations sur les coefficients pour obtenir une matrice triangulaire supérieure puis de faire le produit des valeurs sur la diagonale (voir Wikipedia, cela correspond à la résolution des systèmes linéaires par la technique du pivot de Gauss). Si on a \(n\) lignes et \(n\) colonnes, cela nécessitera de l’ordre de \(n^3\) opérations arithmétiques, donc un nombre polynomial en la taille de la matrice. On peut adapter ce calcul au cas du déterminant en tant que polynôme, qui est donc un polynôme facile au sens du début de cette section.

Le second est le permanent, dont l’expression est la même que celle du déterminant, mais sans la signature : \[\sum_{\sigma \in S_n} \prod_{i=1}^{n} x_{i,\sigma(i)}.\] Ce polynôme étant beaucoup moins bien connu que le déterminant, nous allons en donner ici une inteprétation combinatoire. Considérons un graphe biparti comme celui à gauche dans la figure 18 : c’est un graphe où les sommets sont séparés en deux groupes, ici les roses et les verts, et où les arêtes (les traits) relient toujours un sommet rose à un sommet vert.

Nous supposons aussi qu’il y a autant de sommets roses que de sommets verts. Prenons un exemple pratique, où les sommets roses sont des candidats et les sommets verts des emplois. Les traits indiquent alors si un candidat a les qualifications nécessaires pour un emploi donné. On cherche alors à affecter à chaque candidat un emploi pour lequel il est qualifié. Si on peut faire cela pour chaque candidat et chaque emploi on a ce qu’on appelle un couplage parfait, comme celui en rouge sur la figure de droite.

L’information donnée par la graphe peut aussi être représentée par une matrice. Si on numérote les candidats de \(1\) à \(6\) et les emplois aussi, on va considérer une matrice \(M\) dont le coefficient \(M_{i,j}\) vaudra \(1\) si le candidat \(i\) est relié à l’emploi \(j\) et \(0\) sinon. Dans le cas de notre exemple cela donne : \begin{pmatrix} 1&0&1&0&0&0\\1&0&1&0&0&0\\0&1&0&0&1&0\\0&0&1&0&1&0\\0&0&0&1&0&1\\0&0&1&0&0&1 \end{pmatrix} Affecter un emploi à chaque candidat sans que deux candidats se voient affecter le même emploi revient à choisir une permutation \(\sigma\) indiquant qu'au candidat \(i\) on affecte l’emploi \(\sigma(i)\). Mais encore faut-il que chaque candidat ait bien les qualifications nécessaires à l’emploi qu’on lui a choisi. En utilisant la matrice, cela veut dire vérifier que chacun des \(M_{i, \sigma(i)}\) vaut bien \(1\). On peut vérifier que c’est le cas pour la permutation \(\sigma=\begin{pmatrix} 1&2&3&4&5&6\\ 3&1&2&5&4&6 \end{pmatrix}\) qui correspond à la figure de droite. Une façon de tester cela est de calculer le produit \(\prod_{i=1}^{6} M_{i,\sigma(i)}\), qui ne pourra valoir \(1\) que si tous les coefficients correspondants valent \(1\) et qui vaudra \(0\) sinon. Dans le permanent, on voit apparaître ces termes, sommés pour toutes les permutations possibles. Cela revient à essayer toutes les affectations possibles des emplois aux candidats et à compter \(1\) si l’affectation est un couplage parfait et \(0\) sinon. En résumé, le permanent de la matrice d’un graphe biparti compte le nombre de couplages parfait du graphe.

La simple différence dans la définition du déterminant et du permanent semble impliquer une grande différence pour le calcul, car de nombreux spécialistes pensent que le permanent est dur à calculer. En particulier, ils pensent que, quand la taille \(n\) de la matrice donnée en entrée augmente, le nombre d’opérations nécessaire pour son calcul croît de manière exponentielle en \(n\), ou au moins plus rapidement que n’importe quel polynôme en \(n\).

Le but d’une bonne partie de la recherche dans ce domaine est donc de montrer que VP \(\neq\) VNP. Pour cela on cherche à montrer des bornes inférieures : cela veut dire trouver des exemples explicites de familles de polynômes avec une minoration de la croissance asymptotique du nombre de sommets de calcul nécessaire.

Pour la classe NP il existe des problèmes dits NP-complets qui capturent toute la difficulté de la classe NP par une certaine propriété d’universalité : s’ils sont faciles à résoudre pour un ordinateur alors tous les problèmes de la classe NP le sont aussi. C’est le cas pour la question d’un parcours passant exactement une fois par chaque ville d’une carte. Il suffirait donc de montrer que ce problème n’est pas dans la classe P pour montrer que P \(\neq\) NP.

Il existe de même une notion de complétude pour VNP. Le permanent est VNP-complet et nous aimerions donc montrer qu’un circuit calculant le permanent d’une matrice de taille \(n\) est forcément de taille super-polynomiale en \(n\) (et même exponentielle). Cela impliquerait que VP \(\neq\) NP.

Un résultat modeste grâce à la dérivation

Malheureusement il est difficile de montrer de telles bornes inférieures. Le résultat que nous allons présenter ici est très faible, mais c’est à l’heure actuelle la meilleure borne inférieure pour des circuits arithmétiques sans restrictions particulières (à part la question du degré, que nous laissons de côté). Il est dû à Baur et Strassen et le calcul de dérivées partielles simultanées va y jouer un rôle. L’expression du théorème utilise la notation \(\Omega\) : c’est une façon de comparer l’allure de la croissance asymptotique de fonctions. On dit que \(f\) est \(\Omega(g)\) s’il existe des constantes \(s, a\) telles que, pour tout \(n\geq s\), on a \(f(n) \geq a\cdot g(n)\). Notons aussi que nous considérons ici le cas plus général des circuits avec plusieurs sorties, qui peuvent donc calculer simultanément plusieurs polynômes.

En un sens ce théorème semble évident : si on veut calculer \(x^n\), on peut le faire en élevant successivement au carré : \(x, x^2, x^4, x^8,...\) et pour arriver à la puissance \(n\) il faudra le faire environ \(\log n\) fois. Ensuite il semble raisonnable de penser que, pour calculer cela pour \(n\) variables différentes, il faille multiplier ce nombre d’opérations par \(n\). Cependant, ce théorème n’est pas si facile à montrer et la preuve usuelle s’appuie sur un résultat de géométrie algébrique. Nous admettons le théorème pour continuer.

Le théorème précédent triche un peu : le \(n\) dans la borne inférieure \(\Omega(n \log n)\), c’est-à-dire le terme le plus important, semble dû au fait qu’on demande au circuit de calculer simultanément \(n\) polynômes. Ce qui nous intéresserait ce serait d’avoir une borne inférieure pour le calcul d’un seul polynôme. Nous pouvons remarquer que \(x_1^n,\dots,x_n^n\) sont les dérivées partielles du polynôme \(\tfrac{1}{n+1} (x_1^{n+1} + \dotsb + x_n^{n+1})\). Nous allons donc pouvoir utiliser notre résultat de calcul rapide des dérivées présenté précédemment, qui ici s’exprime par le lemme ci-dessous. Nous utilisons la notation \(O\) réciproque de \(\Omega\) : on dit que \(f\) est \(O(g)\) s’il existe des constantes \(s, a\) telles que, pour tout \(n\geq s\), on a \(f(n) \leq a\cdot g(n)\).

Si nous avions un circuit de taille \(s\) pour le polynôme \(\tfrac{1}{n+1} (x_1^{n+1} + \dotsb + x_n^{n+1})\), alors par notre calcul efficace et simultané des dérivées partielles nous aurions un circuit de taille \(O(s)\) pour calculer simultanément \(x_1^n,\dots,x_n^n\), et la borne inférieure précédente s’appliquerait. On obtient donc le résultat suivant.

Insistons encore une fois sur la faiblesse de notre résultat, même s’il est le meilleur à ce jour. Pour séparer VP et VNP, il nous faudrait une borne inférieure super-polynomiale, donc croissant plus vite que tout polynôme en \(n\), alors qu’ici nous avons une borne qui croît à peine plus vite que linéairement en \(n\).

Mathématique et informatique, théorie et applications

Nous venons donc de voir comment une même technique de calcul de dérivées peut servir à la fois en pratique pour l’apprentissage machine et en théorie pour la complexité algorithmique. Cet exemple, qui est loin d’être unique, nous permettrait de conclure sur les liens étroits entre les applications et la théorie, mais aussi entre différents domaines des mathématiques ou de l’informatique. Nous allons cependant ajouter une dernière courte illustration de ce phénomène.

La descente de gradient que nous avons vue correspond à une approximation locale linéaire de la fonction d’erreur. On pourrait imaginer utiliser aussi les dérivées partielles secondes et se demander s’il existe un calcul simultané et efficace de celles-ci. Un argument simple permet de voir que cela impliquerait un calcul rapide du produit matriciel.

La façon naïve de multiplier deux matrices carrées \(A\) et \(B\) de taille \(n\) nécessite un nombre \(O(n^3)\) d’opérations : pour chacun des \(n^2\) coefficients du résultat \(C\), il faut faire \(n\) multiplications et \(n-1\) additions.

Considérons maintenant deux vecteurs \(X = (x_1,\dots,x_n)\) (en ligne) et \(Y=(y_1,\dots,y_n)\) (en colonne). On peut alors calculer le produit \(X\cdot A\) en \(O(n^2)\) opérations. De même pour \(B\cdot Y\). Puis le produit \((XA)\cdot (BY)\) est un produit scalaire et se fait en \(O(n)\) opérations. Donc au total cela nécessite \(O(n^2)\) opérations.

Remarquons ensuite que la dérivée partielle \(\tfrac{\partial (XABY)}{\partial x_i \partial y_j}\) est le coefficient \((i,j)\) du produit \(AB\). Si on pouvait calculer simultanément toutes ces dérivées partielles secondes en multipliant la taille du calcul seulement par une constante, alors on aurait un calcul du produit matriciel en \(O(n^2)\) opérations. Or, s’il est possible de faire mieux que l’algorithme naïf, avec un exposant de \(n\) qui est compris entre \(2\) et \(3\), et qu’on arrive régulièrement à faire baisser et donc à rapprocher de \(2\), il n’est pas clair qu’un algorithme en \(O(n^2)\) existe. Notons d’ailleurs qu’un algorithme en \(O(n^2)\) est ce qu’on peut espérer de mieux, puisqu’il faut au moins une opération par coefficient du résultat.

On peut enfin se demander pourquoi il ne suffit pas d’appliquer deux fois notre calcul efficace de toutes les dérivées partielles simultanément : puisque celui-ci multiplie la taille du calcul par une constante, l’appliquer deux fois ne devrait pas poser problème. La faille réside dans le fait qu’après la première application, nous avons un calcul simultané des \(\tfrac{\partial f}{\partial x_i}\), et nous avons besoin de toutes les dérivées partielles de toutes ces fonctions, et non pas d’une seule. En revenant à nos calculs de chemins, nous aurions besoin de la somme des poids des chemins entre \(O(n^2)\) paires de sommets, au lieu de la somme des poids des chemins entre \(O(n)\) sommets et un sommet cible.

Dit autrement, ce lien avec la multiplication de matrices montre qu’il est peu probable qu’on ait un « cheap Jacobian principle » similaire à notre « cheap gradient principle ». En nous pouvons revenir à notre conclusion, heureusement largement reconnue désormais en mathématique et informatique, sur l’enrichissement mutuel des applications et de la théorie.

Pour aller plus loin

• Patterns, Predictions, and Actions: A story about machine learning, Moritz Hardt and Benjamin Recht: un livre sur l'apprentissage machine.

• Arithmetic Circuits : a survey of recent results and open questions, Shpilka & Yehudayoff 2010: une présentation assez détaillée de la complexité algébrique et des questions sur les circuits arithmétiques. Le document se trouve aussi sur la page d'Amir Shpilka.

• https://github.com/dasarpmar/lowerbounds-survey : une autre présentation de la complexité algébrique, document coopératif maintenu par Ramprasad Saptharishi.

• Who Invented the Reverse Mode of Differentiation ?, Andreas Griewank : une présentation historique  de l'invention de la technique de calcul à l'envers des dérivées partielles. Disponible en ligne ici.