Créer des groupes n'est pas toujours facile. Pour regrouper les éléments proches entre eux, des méthodes existent. Mais il faut pour cela savoir déterminer la proximité.
Faire des groupes est un vrai casse-tête. Parfois, on connaît le nombre de membres souhaité dans chaque groupe. En classe, on forme des binômes pour des activités. Parfois, on connaît le nombre de groupes et on veut simplement répartir les différents membres dans ces groupes. Par exemple, à partir des Français, on crée le groupe des personnes mineures (les personnes ayant moins de 18 ans) et celui des personnes majeures. À ce moment-là, les groupes peuvent avoir des tailles différentes : il y a par exemple bien plus de majeurs que de mineurs en France.
Le problème qui se pose parfois quand le nombre de membres n'est pas important, c'est de savoir comment répartir les membres dans les groupes. Dans le cas des groupes de mineurs et de majeurs, c'est facile, mais prenons un autre exemple : une course cycliste.
Dans une course cycliste, on se retrouve souvent, au fur et à mesure de la course, dans la configuration suivante :
Dans ce cas, comment faire pour regrouper les cyclistes? On pourrait décider de faire des groupes en fonction de leur classement : les 6 premiers, les 6 du milieu, les 6 derniers.
Cependant, on préfère généralement créer trois différentes catégories : ceux en tête, ceux en retard, et le peloton.
Dans ce cas, comment décide-t-on des membres de chaque groupe ? La réponse se trouve dans le choix de la distance : les membres du peloton sont proches les uns des autres, et éloignés des autres cyclistes.
Bien choisir sa distance
Une distance correspond à une valeur représentant l’éloignement entre deux choses. La manière dont on la calcule va dépendre de la distance voulue.
Prenons l'exemple du trajet Paris-Bordeaux. Il est possible de définir plusieurs distances différentes pour ce trajet :
- Distance « en voiture » : la distance la plus courte à parcourir en voiture pour aller d'un endroit à un autre. La distance Paris-Bordeaux est de 584 km.
- Distance « à vol d'oiseau » : la distance la plus courte à parcourir en volant pour aller d'un endroit à un autre. La distance Paris-Bordeaux est de 500 km.
- Distance « en temps » : le temps le plus court pour aller d’un endroit à un autre, quel que soit le moyen de locomotion. La distance Paris-Bordeaux, en avion (le moyen de transport le plus rapide), s’effectue en 1h10.
Comme le montre la distance « en temps », la distance n’est pas nécessairement une mesure en mètre, kilomètre ou centimètre.
En fait, il existe une infinité de manières de définir une distance. Il y a simplement besoin de respecter quelques règles :
- La distance d'un endroit à lui-même est de 0. Par exemple, si je suis à Bordeaux, la distance (en temps, à vol d’oiseau ou en voiture) jusqu'à Bordeaux est de 0. C'est le principe de séparation.
- La distance aller est la même que la distance retour. Par exemple, la distance Paris-Bordeaux (en temps, à vol d’oiseau ou en voiture) est la même que la distance Bordeaux-Paris. C'est le principe de symétrie.
- Faire un détour ne diminue jamais la distance. La distance Paris-Lyon (en temps, à vol d’oiseau ou en voiture) ajoutée à celle de Lyon-Bordeaux n'est pas plus petite que la distance Paris-Bordeaux. C'est le principe de l'inégalité triangulaire.
symétrie ∀ (a,b) ∈ E2 , d(a,b) = d(b,a)
séparation ∀ (a,b) ∈ E2 , d(a,b) = 0 ⇔ a = b
inégalité triangulaire ∀ (a,b,c) ∈ E3 , d(a,c) ≤ d(a,b) + d(b,c)
Ainsi, les distances peuvent prendre des formes diverses et variées pour comparer toutes sortes d’éléments entre eux. Par exemple, on peut déterminer des distances entre des mots en déterminant une distance permettant de passer d’un mot à l’autre.
Prenons l’exemple des mots papa et papy.
Si on autorise à enlever et à ajouter des lettres, alors il faut enlever un a et ajouter un y pour passer du premier au deuxième. Cette distance est de 2 (on appelle cette distance la distance d’édition).
Si, en revanche, on autorise à remplacer des lettres, alors simplement remplacer a par y suffit. Cette distance est de 1 (on appelle cette distance la distance de Hamming).
En fait, en définissant une distance entre les éléments, on met ces éléments en relation les uns aux autres. Il est alors possible de comparer les éléments entre eux.
Maintenant qu'on sait comment fabriquer une distance pour comparer des éléments, essayons d’utiliser cette distance pour faire des groupes !
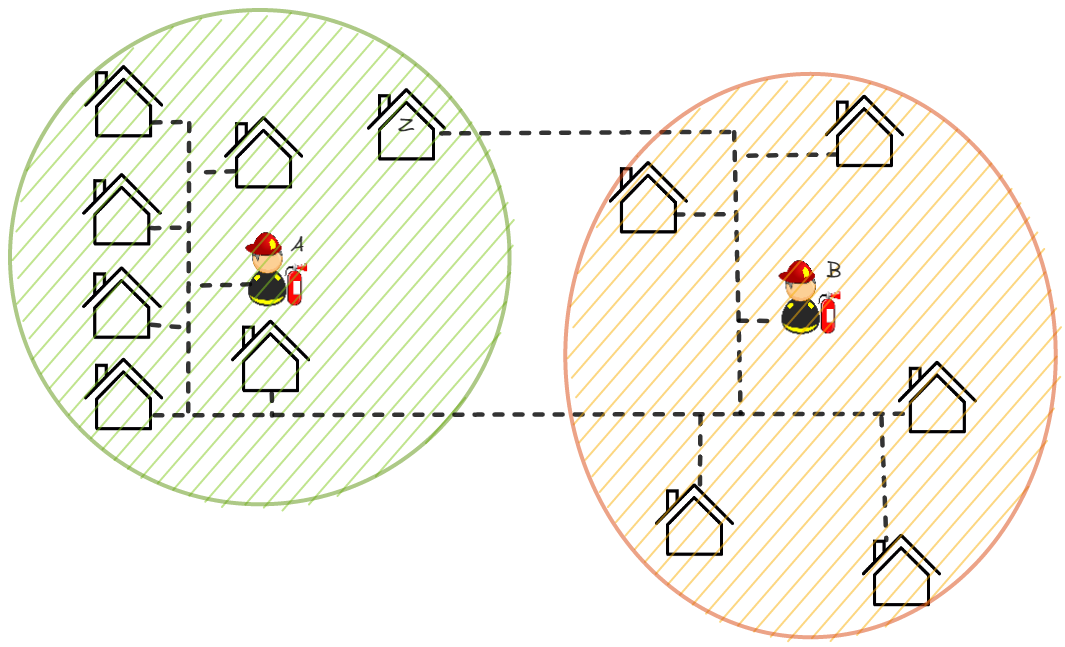
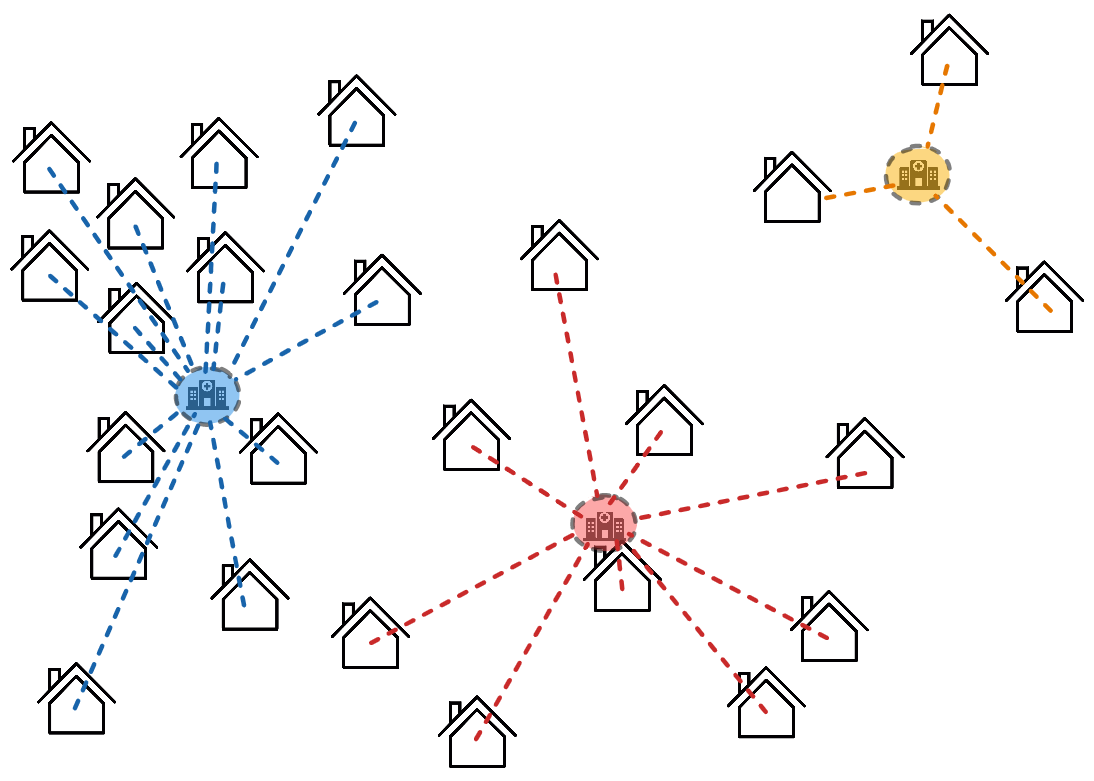
Imaginons deux casernes de pompiers dans une petite ville. On peut par exemple répartir les maisons en deux groupes en fonction de la distance à « vol d'oiseau » (qui est aussi appelée distance euclidienne) : chaque maison appartient au groupe de la caserne qui est la plus proche en termes de distance.
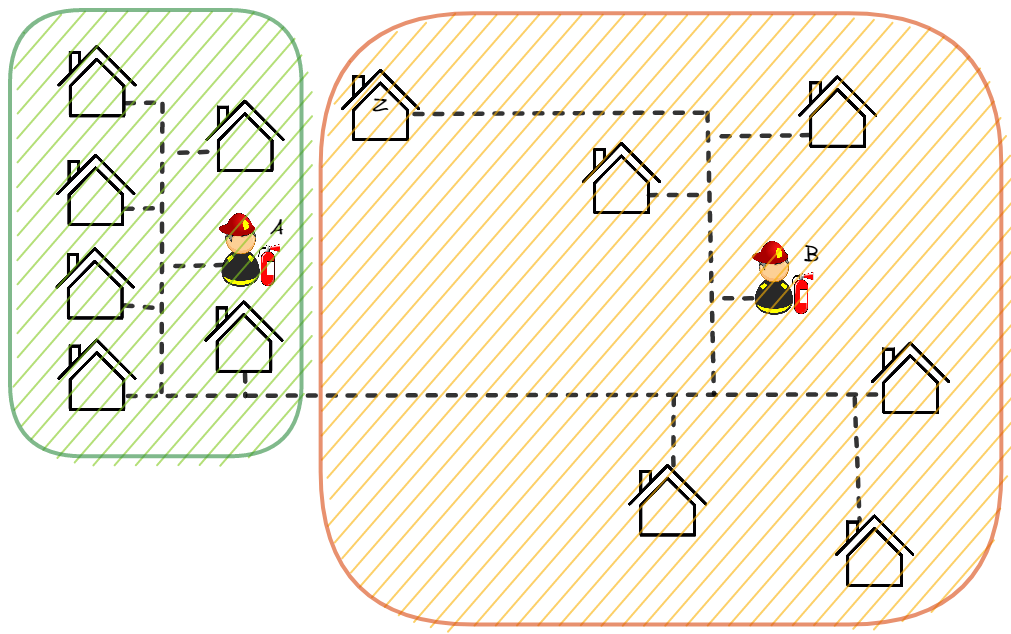
On voit bien l'importance du choix de la distance. La maison Z est reliée à la caserne A, mais en réalité, si les pompiers devaient intervenir avec leur camion, ils auraient plus de chemin à parcourir que ceux de la caserne B. Dans ce cas, il faut plutôt choisir une distance « routière » (avec des routes en double-sens pour respecter la symétrie). De cette manière, les groupes se trouvent chamboulés :
On s'aperçoit donc de l'importance du choix de la distance quand on cherche à créer des groupes.
Créer des groupes à partir de la distance
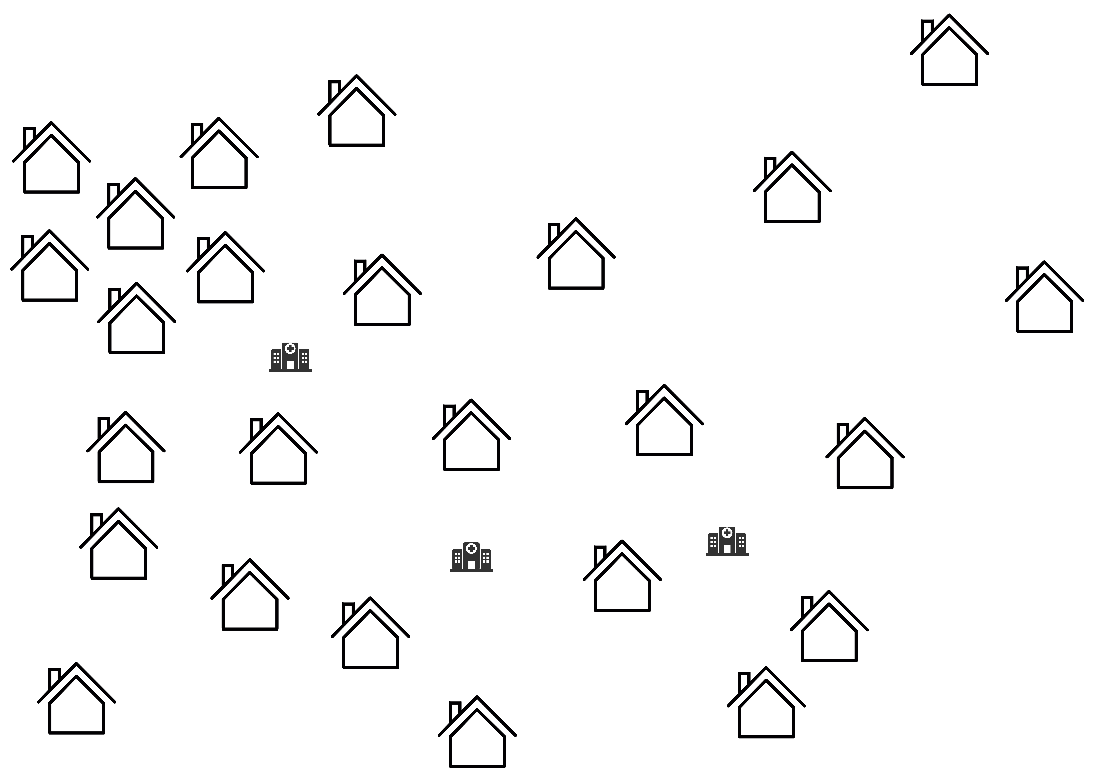
Maintenant, prenons le problème à l'envers. On a choisi notre distance et on sait combien de groupes on veut. Par exemple, imaginons qu'il y ait besoin, dans une ville, de choisir les endroits où construire 3 hôpitaux munis d'hélicoptères sanitaires. Il faut donc créer un groupe de maisons par hôpital.
On peut alors utiliser des méthodes pour faire apparaître des regroupements. Essayons-en une.
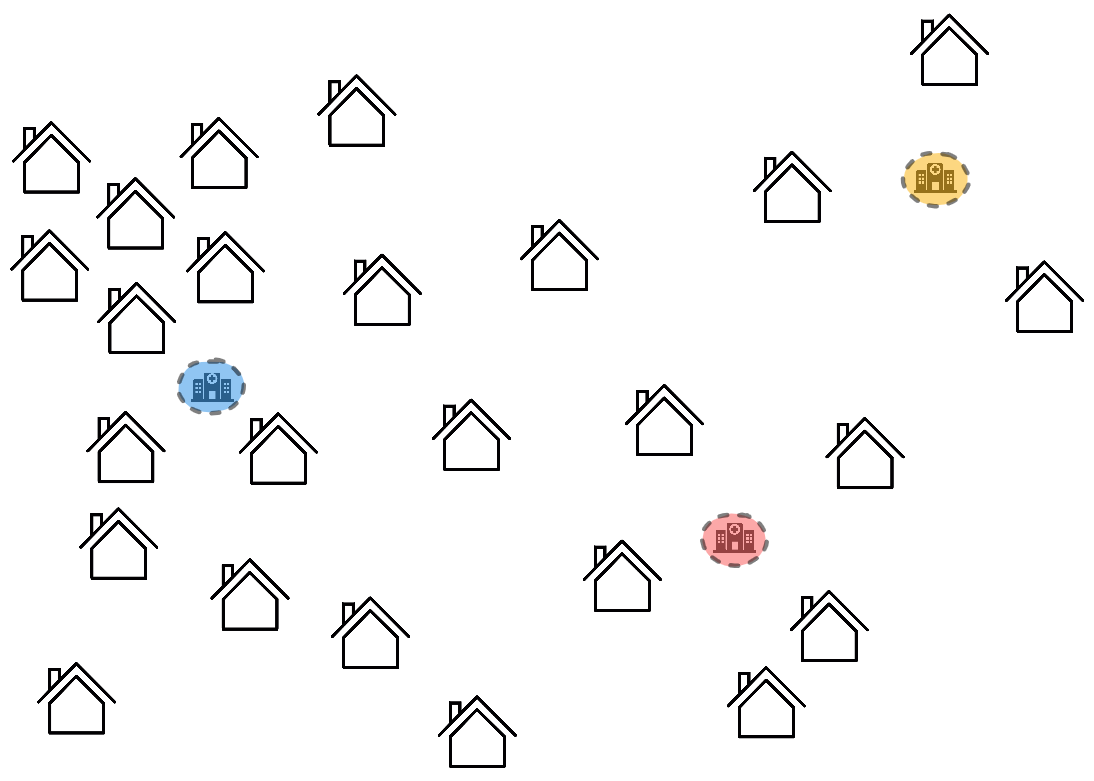
D'abord, on choisit une distance et un nombre de groupes : on choisit la distance à « vol d'oiseau » (parcourue par les hélicoptères) et on souhaite créer 3 groupes, un par hôpital. On sélectionne alors 3 endroits de départ pour nos hôpitaux :
Ces endroits vont changer au fur et à mesure pour qu'ils soient plus intéressants en termes de distance, c'est-à-dire qu'ils soient en moyenne plus proches des maisons qui leur seront associées.
Ensuite, comme pour le cas des casernes de pompiers, on associe chaque maison à l'hôpital le plus proche.
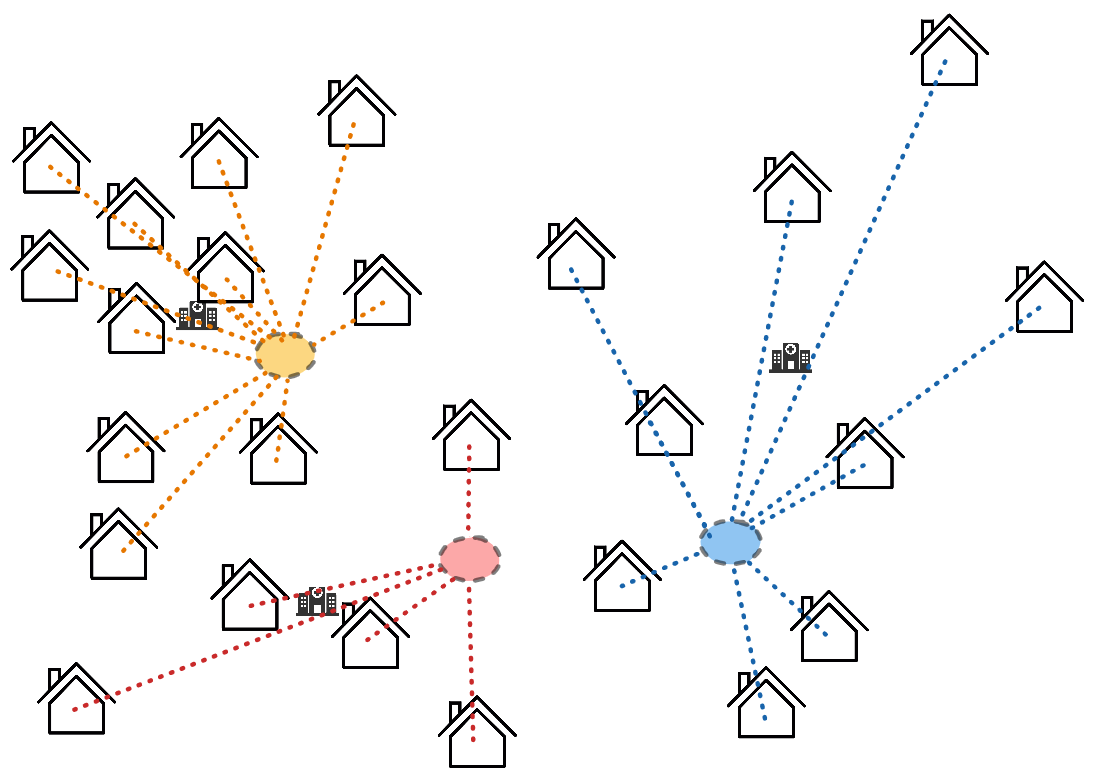
Ensuite, on déplace les hôpitaux pour essayer de minimiser les distances reliant l'hôpital aux maisons qui lui sont associées. Intuitivement, on souhaite le mettre au centre du groupe des maisons. Les centres des ensembles de points sont appelés centroïdes: ce sont les moyennes des positions des points du groupe1. Dans notre cas, on obtient les positions des hôpitaux suivantes :
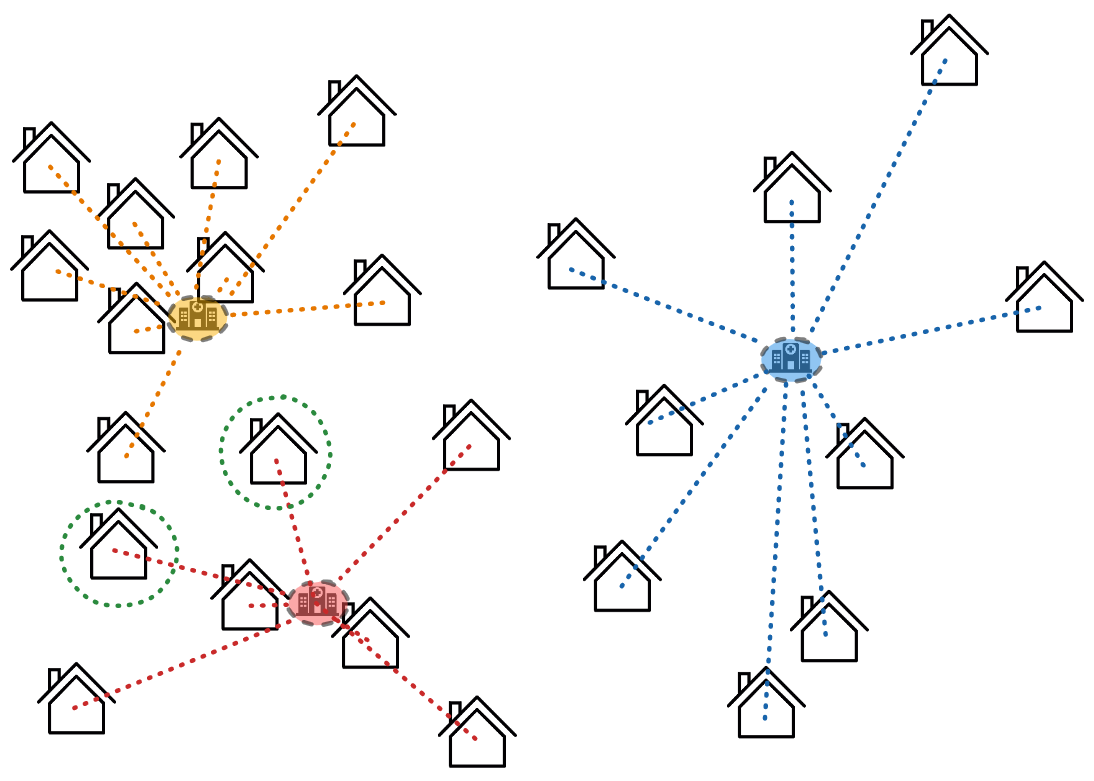
Une fois qu'on a les nouvelles positions des hôpitaux, on peut assigner de nouveau les maisons à l'un des trois hôpitaux.
Dans notre exemple, les deux maisons entourées en vert ont changé de groupe.
On alterne donc le déplacement des positions des hôpitaux vers le centroïde de leur groupe et la réassignation des maisons à un des 3 hôpitaux, jusqu'à ce que plus rien ne bouge.
Cet algorithme est généralement appelé algorithme des k-moyennes (ou algorithme de Lloyd) et peut se résumer ainsi :
1. Choisir k points de référence (ex : emplacement d'hôpital) dans l'espace des données, k étant le nombre de groupes voulu ;
2. Assigner chaque donnée (ex : maison) au point parmi les k qui est à la plus proche distance, ce qui forme k groupes ;
3. Calculer le centroïde (le point moyen d'un groupe) pour chaque groupe. Ces centroïdes deviennent les k nouveaux points de référence (ex : nouvel emplacement d'hôpital) ;
4. Recommencer 2. et 3. jusqu'à ce que les centroïdes restent les mêmes (on dit qu'on continue jusqu'à ce que l'algorithme converge).
Cet algorithme est pratique, mais il a quelques défauts. D'abord, en fonction de la distance choisie, l'algorithme peut ne jamais converger et donc ne jamais s'arrêter.
Ensuite, cet algorithme ne donne pas forcément le même résultat en fonction des points choisis au départ.
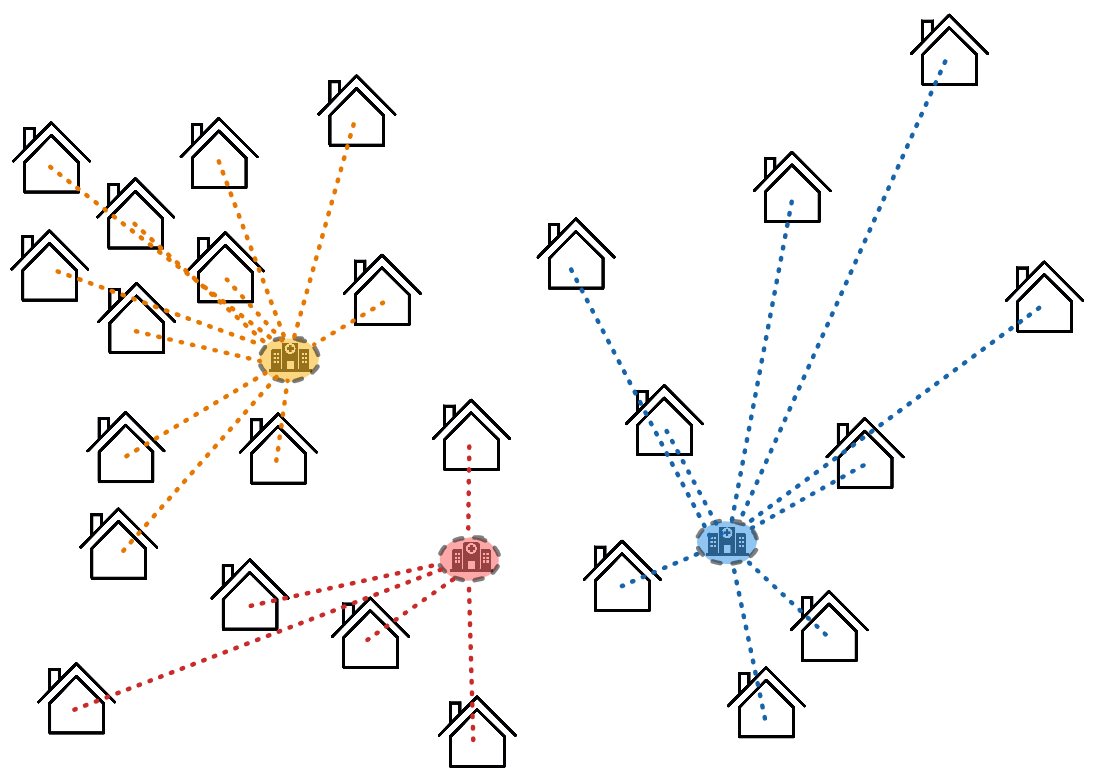
Si on sélectionne d'autres endroits de départ pour les hôpitaux, alors on peut obtenir des résultats différents.
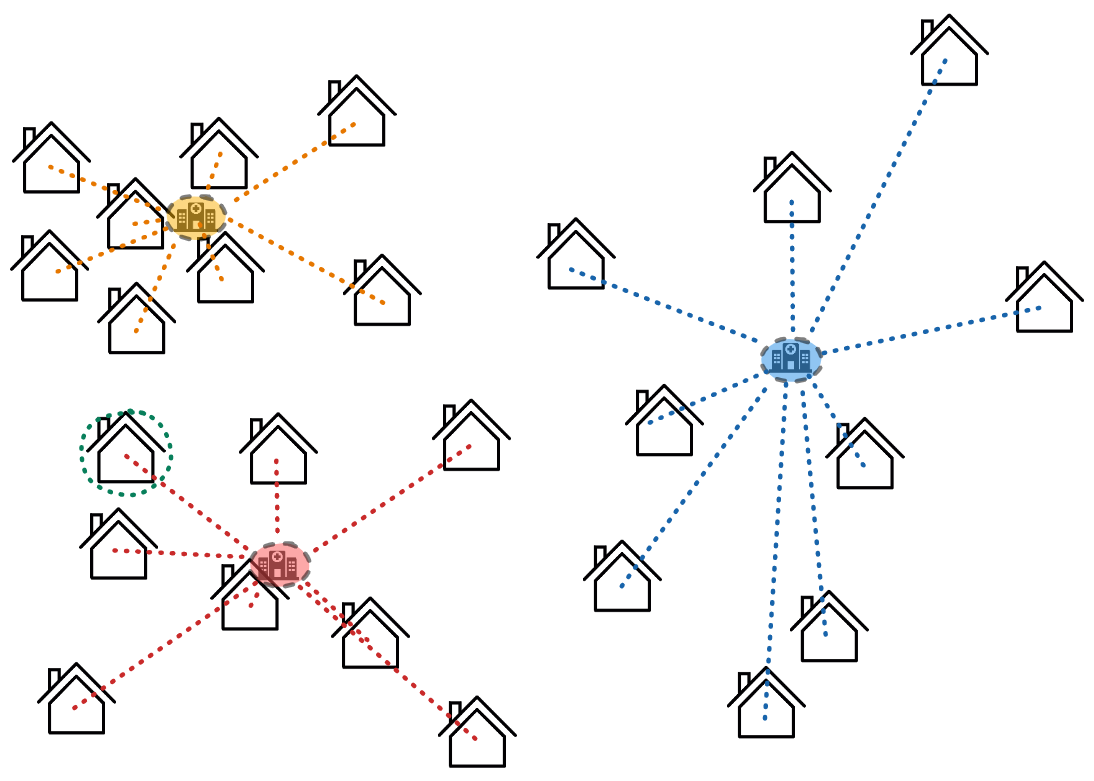
L'image ci-contre propose d'autres positions initiales pour les hôpitaux.
Après application de la méthode détaillée plus haut, les groupes obtenus sont différents.
Ainsi, si on cherche à utiliser cette méthode pour déterminer ou placer des hôpitaux, il est généralement intéressant d'appliquer cette méthode sur de nombreuses positions initiales pour pouvoir faire le meilleur choix possible.
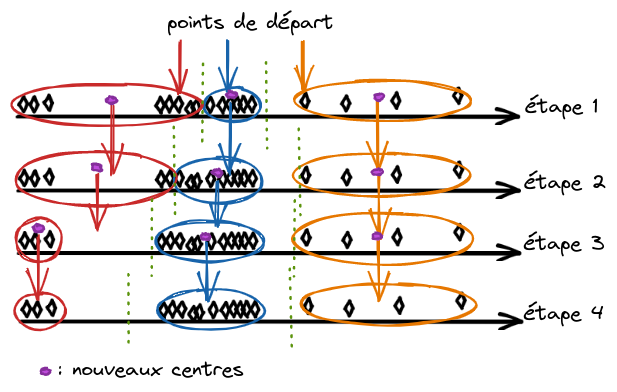
Chose amusante, on peut se servir de cette méthode pour recréer les groupes pour nos cyclistes :
- On prend trois points de départ dans la course qui seront nos premiers points de référence ;
- On associe chaque cycliste au point le plus proche ;
- Les centres des groupes (les flèches) créés deviennent les nouveaux points de référence pour les regroupements, et on recommence ;
- A la fin, on obtient 3 groupes, et on a séparé le peloton des premiers et des derniers.
Cet algorithme fait partie d'une catégorie d'algorithmes permettant de faire des regroupements qu'on appelle des algorithmes de clustering (ou algorithmes de regroupement)1.
Conclusion
Il existe de nombreuses méthodes pour créer des groupes : on peut vouloir créer des groupes de tailles précises, ayant des caractéristiques précises etc.
Mais quand on ne sait pas comment s'y prendre, les techniques de clustering, comme celle des k-moyennes par exemple, sont là pour aider à générer des groupes. Quand on dispose d'un nombre important de données, dans les domaines relatifs à ce qu'on appelle la Big Data par exemple, on se retrouve souvent à vouloir créer des groupes afin de pouvoir s'intéresser à des sous-parties de grands jeux de données.
Mais dans tous les cas, pour que de tels regroupements soient possibles, il faut savoir prendre de la distance, et choisir avec soin celle qui s'adapte à notre problème.