Pour peu que l’on s’intéresse à l’histoire de la déficience visuelle dans la société, on identifie facilement quelques noms de personnes concernées ayant marqué la discipline mathématique. On pense immanquablement à Leonhard Euler, qui a poursuivi sa pratique scientifique abondante pendant près de dix ans après avoir perdu complètement la vue. Plus récemment, on peut aussi citer Bernard Morin (1931-2018), topologue français ayant découvert plusieurs surfaces et paramétrisations originales. Concerné par la cécité depuis l’âge de six ans, il a donc bénéficié d’un enseignement mathématique adapté à son handicap. Louis Antoine (1888-1971), lui aussi topologue et géomètre, perd la vue pendant la guerre 14-18. On retient notamment son nom parce qu’il a mis au point de la notation braille des symboles mathématiques encore en usage aujourd’hui. Dans cet article, nous présentons différents outils, fréquemment utilisés par les personnes en situation de cécité, pour lire et écrire les mathématiques, depuis l’algèbre et l’analyse jusqu’aux représentations géométriques et graphiques de fonctions.

Noter l’algèbre et l’analyse

Le système braille d’écriture tactile est aujourd’hui la technique de référence enseignée par toutes les écoles à travers le monde aux personnes aveugles. Inventée par Louis Braille au début du XIX^e siècle, cette technique permet de transcrire chaque lettre d’une phrase en son équivalent braille, souvent constitué d’une seule cellule, parfois de deux. Chaque cellule du braille standard est composée de six points distribués sous forme d’une matrice de deux colonnes, chaque caractère étant formé par un à six points en relief, ce qui permet de coder jusqu’à 63 signes différents (auquel on ajoute l’espace, caractère blanc). Comme beaucoup d’alphabets nécessitent de décrire plus de 63 signes, il est convenu que certains caractères (appelés clés) serviront de préfixe pour annoncer une interprétation différente des signes suivants. Pour transcrire les alphabets latins, et en particulier un texte en français, on utilisera par exemple un caractère braille pour indiquer que la lettre qui suit est en majuscule, ou encore qu’il s’agit d’un nombre : ce sont les clés qui servent à modifier la valeur du caractère braille qui suit.

Car, bien sûr, on peut noter les mathématiques à l’aide du braille. La pratique et les recommandations ont beaucoup évolué depuis le XIX^e siècle, pour converger vers le système pratiqué aujourd’hui 1, s’appuyant sur une représentation linéarisée de l’information. Un peu à la manière du $\LaTeX$, on va transcrire une équation par sa notation linéaire, puis utiliser des symboles caractéristiques, pour chacun des éléments qui composent les équations. La limitation des 63 signes évoquée plus haut impose alors d’utiliser des assemblages de signes braille pour décrire un grand nombre de symboles mathématiques. Cependant, la lecture au doigt nécessitant une grande concentration, on a privilégié au maximum la concision des formules, en choisissant un peu à la manière du codage de Huffman de représenter les symboles récurrents (chacun des chiffres, les parenthèses, mais aussi des fonctions comme sinus ou racine carrée) par un seul symbole, quand les moins récurrents pourront être représentés par plusieurs symboles.

La table suivante (Figure 1) donne un tableau d’équivalence pour quelques symboles mathématiques, en montrant leur équivalent $\LaTeX$ et braille.

La figure 2 présente une formule sous quatre formes, pour illustrer la diversité d’encodage.

À l'aide de la dernière colonne de la figure 1, sauriez-vous à présent représenter la saisie clavier des caractères braille composant  la formule de la figure 2 ?2

Géométrie et représentations graphiques

L’autre élément indispensable à la pratique des mathématiques, ce sont les représentations graphiques. Dès le primaire puis au secondaire, on sollicite le tracé pour travailler la géométrie dans le plan, mais aussi les représentation graphique de fonctions. Outil indispensable de la transmission, on se doit de proposer aux élèves étudiant les mathématiques une solution pour au moins consulter des représentations graphiques.

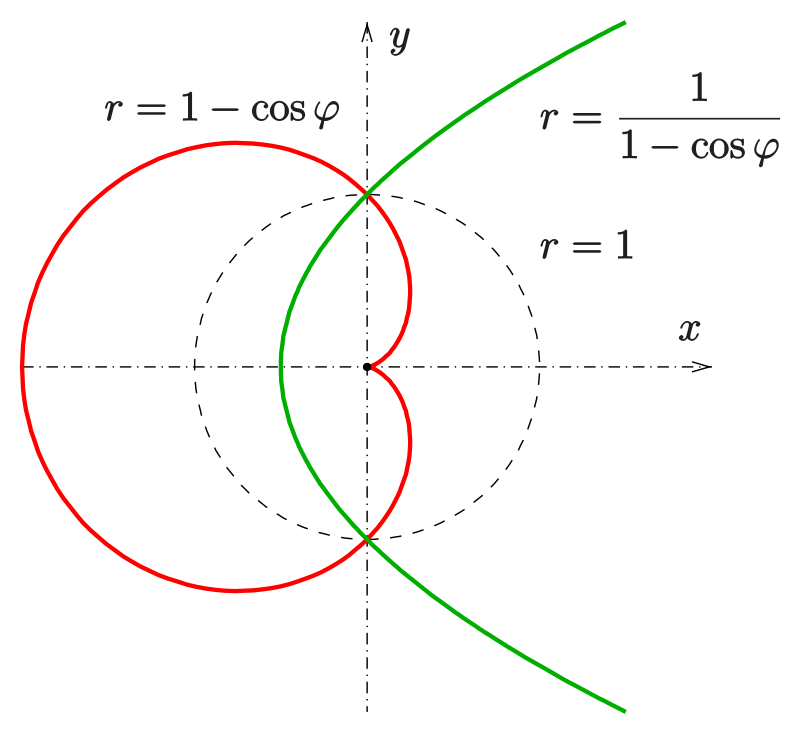
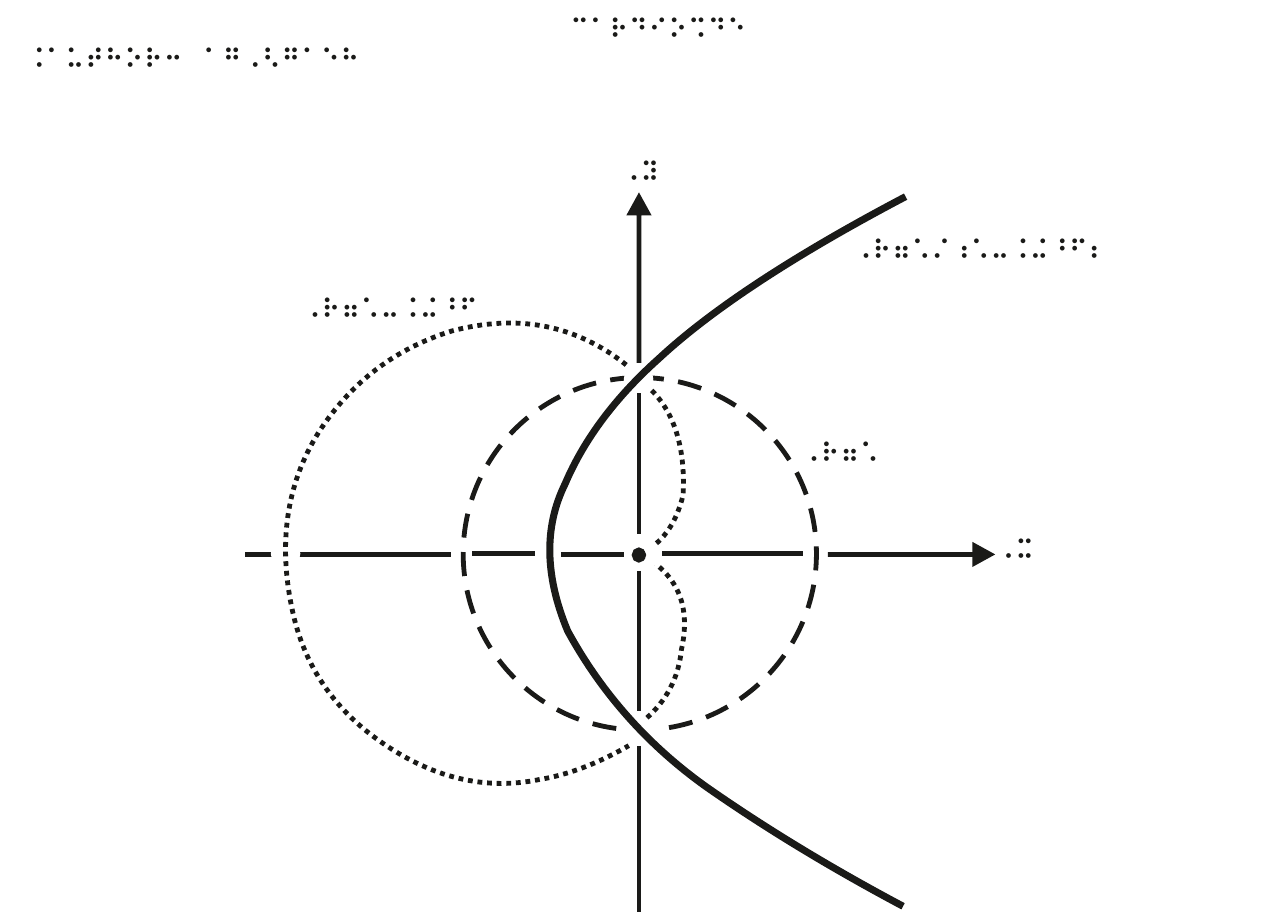
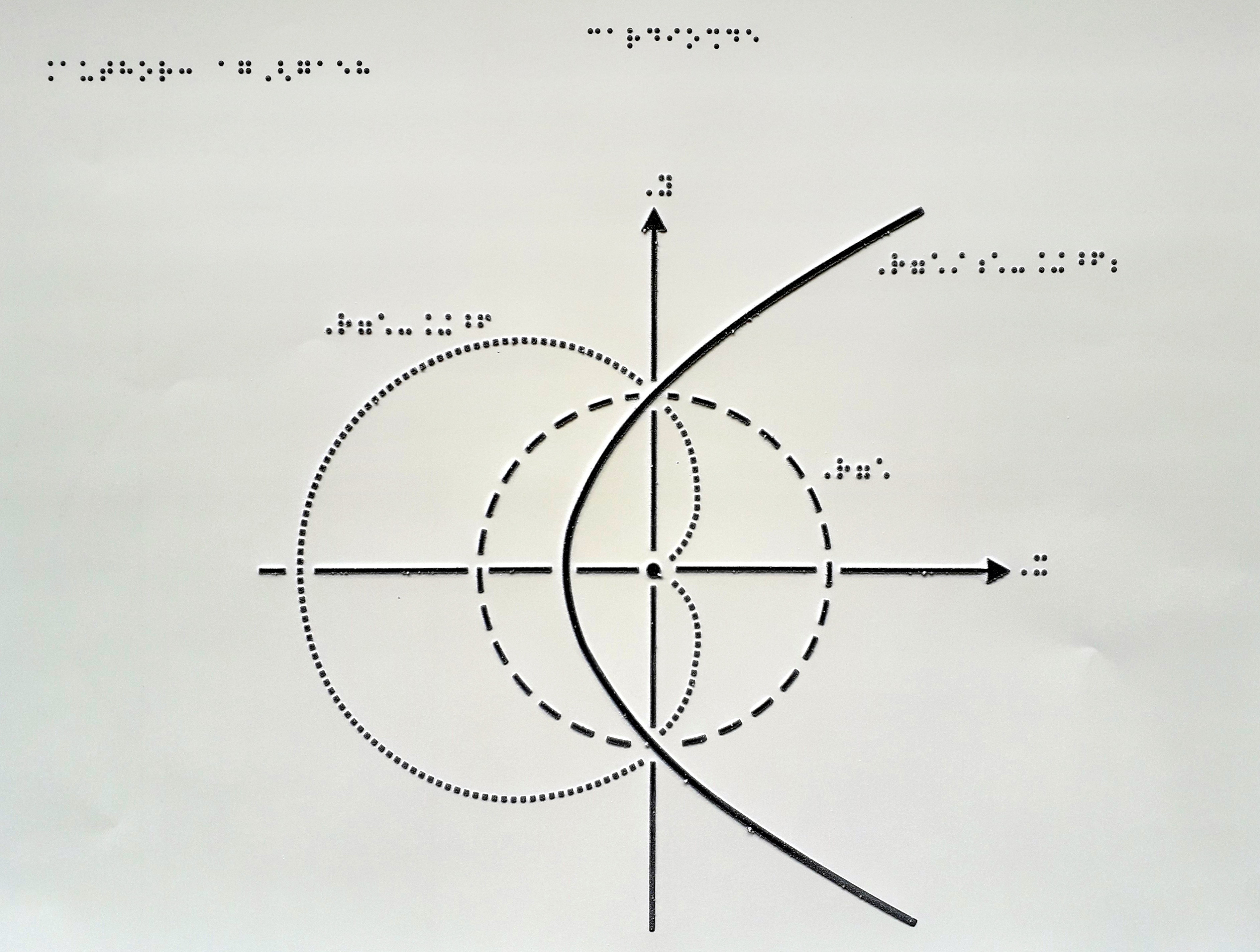
En reprenant le principe du braille, on imagine assez bien une représentation en relief, où les coups de crayon seraient remplacés par des traits en relief. En XXI^e siècle, la solution la plus répandue consiste à utiliser un papier spécial, dit thermogonflé, que l’on passe quelques secondes à haute température pour faire gonfler les parties imprimées en noir. Combiné à une imprimante classique, c’est la solution que privilégient aujourd’hui la plupart des adaptateurs-transcripteurs quand ils préparent les schémas, diagrammes et représentations graphiques pour le public déficient visuel, comme l’illustre la figure 3.

Un autre outil en perte d’usage est également utilisable directement par les personnes concernées. Elle se compose d’une planche de matières souple, la planche Dycem, combinée à une feuille en plastique tramé, que l’on vient bosseler (cette fois-ci directement sur le recto) en traçant avec un stylo bille par exemple.

Cependant, quelle que soit la technique utilisée, il faut garder à l’esprit que même pour la personne la plus exercée, les détails identifiables sur un dessin en relief est bien moindre que la finesse des détails que l’on peut voir avec les yeux. La pulpe des doigts est certes très sensible, mais elle ne permet pas de descendre dans l’interstice entre deux formes si elles sont trop proches, on ne pourra pas distinguer beaucoup de textures différentes, ni des changements de taille ou de position subtils. Le travail des adaptateurs-transcripteurs consiste donc ici à travailler sur une simplification des éléments représentés, en faisant des choix, en privilégiant la lisibilité plutôt que la quantité, et en s’adaptant à chaque fois à la personne à qui le document est destiné. On pourra par exemple décomposer une figure en plusieurs figures relief, afin de rendre accessible la totalité des informations, ou encore travailler sur des espaces supplémentaires, appelés blanc de confort, pour permettre au lecteur de percevoir deux éléments distincts.

Même avec cet important travail d’adaptation, la lecture de représentations graphiques au doigt est un exercice réellement difficile, qui nécessite un long travail d’apprentissage aux personnes en situation de déficience visuelle.

Étudier les mathématiques aujourd’hui

Si la lecture du braille est aujourd’hui une compétence incontournable par la plupart des non voyants en âge d’être scolarisés, on observe une grande disparité à travers le monde quant aux pratiques d’accès au contenu écrit, qu’il soit mathématique ou non. L’outil informatique a apporté des facilités qui sont précieuses, amenant notamment la synthèse vocale comme outil alternatif à la lecture tactile. En France, la plupart des jeunes en situation de déficience visuelle ont accès à une version retranscrite de leurs supports de cours. Cependant, si l’école inclusive a permis en théorie un accès universel à l’enseignement, on observe tout de même de grande disparités suivant les établissements d’accueil 3, et leur proximité à des services de transcription-adaptation. Il n’est pas rare de rencontrer des jeunes qui n’ont pas pu faire les choix d’orientation auxquels ils se destinaient par manque d’accès à une transcription à la hauteur des besoins de la formation.