Quel rapport étrange pourrait-il y a voir entre $\displaystyle \frac{1}{4}$ et $\displaystyle \frac{1}{3}$ ? Ce sont deux nombre que l'on dit rationnels, car ils sont représentés par une fraction dont le numérateur et le dénominateur sont tous les deux des entiers naturels. Le premier vaut $0,25$ très précisément, alors que pour le second, il faut une répétition infinie de $3$ pour le décrire : $\displaystyle \frac{1}{3}=0,33333\dots$.

L'écart entre les deux nombres n'est pas plus simple. C'est $\displaystyle \frac{1}{3}-\frac{1}{4}= \frac{1}{12}$, et il faut encore une infinité de chiffres après la virgule si on veut en donner une écriture décimale. En tout cas, il semblerait bien qu'il faille faire un détour par l'infini pour saisir le lien entre ces deux nombres.

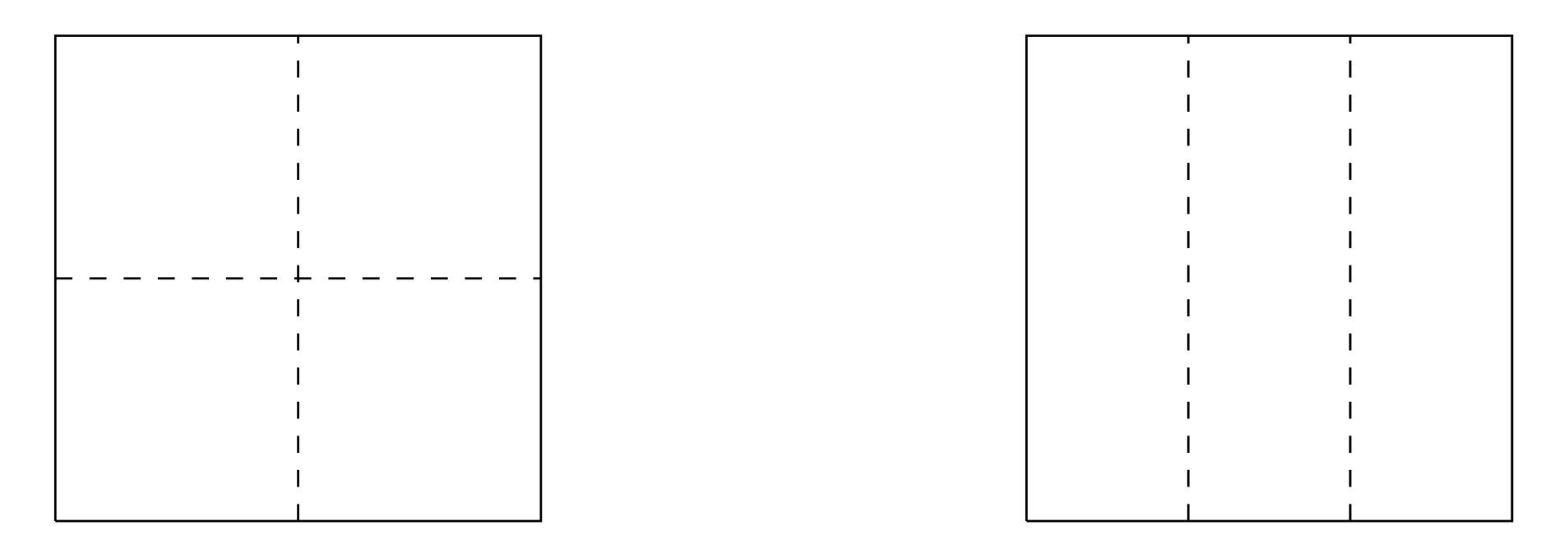
En fait, ces deux nombres sont intimement liés dans la vie de tous les jours et dans des situations très simples. Par exemple, si on prend un carré, disons de côté $6$ cm, il est très facile de le couper soit en $3$ soit en $4$.

Notre carré avait une surface de $6\times 6=36$ cm, les quatre carrés représentent chacun le quart de cette surface, soit $9~\textrm{cm}^2$, alors que les rectangles qui représentent le tiers de la surface correspondent chacun à $12~\textrm{cm}^2$.

Grâce à ce dessin et au calcul des aires, le tiers et le quart ne sont pas si étrangers l'un à l'autre que l'on pourrait-on penser : $9~\textrm{cm}^2$ d'un côté, $12~\textrm{cm}^2$ de l'autre, un écart entre les deux de $3~\textrm{cm}^2$, des nombres bien ronds, bien entiers ! Mais si on y regarde de plus près, et surtout par le biais des rapports, $\displaystyle \frac{12}{9}=\displaystyle \frac{4}{3}=\displaystyle \frac{\frac{1}{4}}{\frac{1}{3}}$, on retombe sur notre problème initial...

La passage par l'infini est donc inéluctable. Pour aller du quart au tiers, on va employer une méthode que l'on peut retrouver dans une vidéo très bien faite de Pierre Arnoux (cliquez sur le lien ici). On reprend ici les étapes afin de relier le quart au tiers.

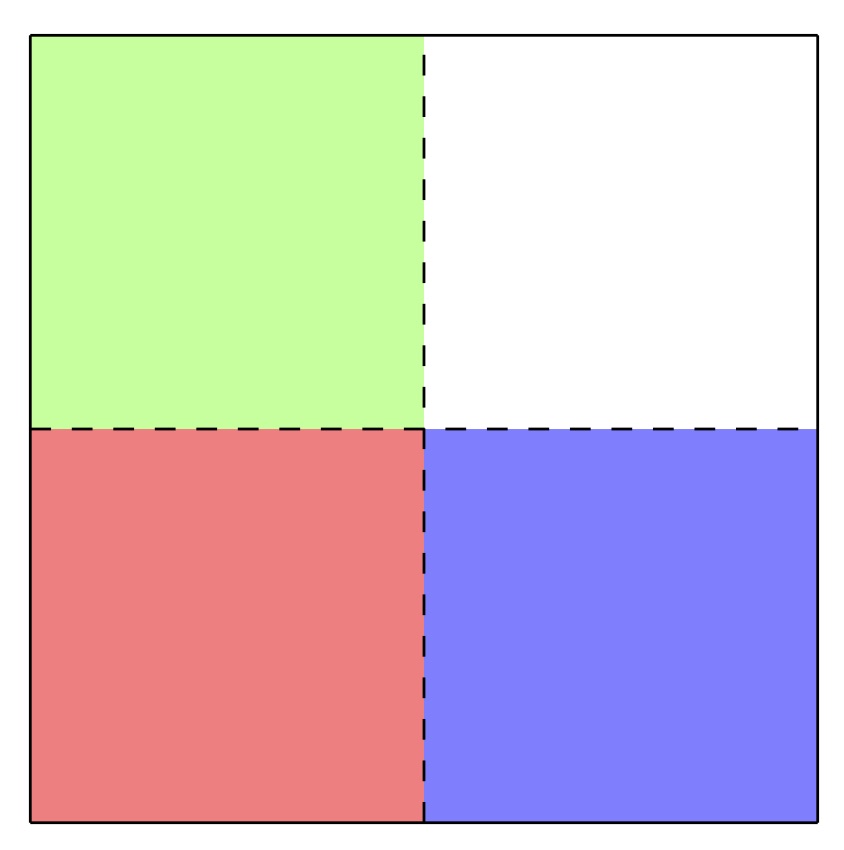
D'abord on part du carré et de sa découpe très facile en quatre parts égales. Pour constituer notre tiers final, on va distribuer des morceaux du carré en 3 parties égales, l'une en rouge, l'autre en vert et enfin la dernière en bleu. Quand on aura fini, sans sortir de la figure de départ, on aura donc découpé notre carré en trois parties de même aire.

On commence donc de la façon suivante :

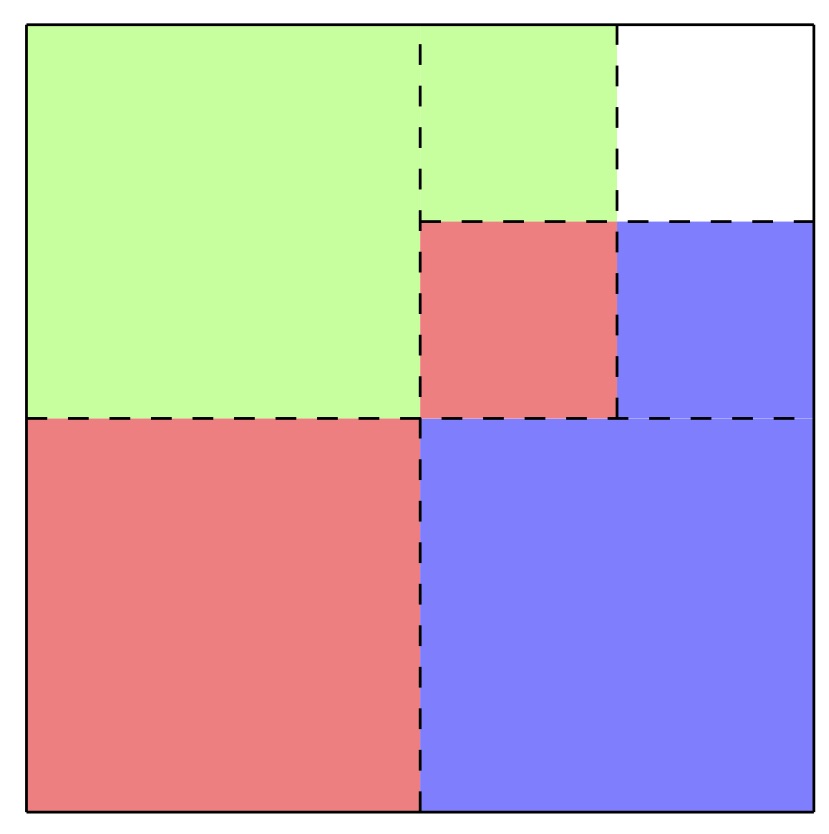
Puis on recommence avec le carré blanc que l'on découpe en 4 pour distribuer 3 parties égales :

On voit s'amorcer un joli remplissage coloré qui respecte bien que les surfaces coloriées en bleu, en rouge ou en vert sont exactement de même aire. Si l'on prolonge cette stratégie à l'infini, on aura rempli tout notre carré initial.

Donc, d'un point de vue algorithmique, on a une opération simple (découpe d'un carré en 4 parties égale, et coloriage en 3 couleurs), que l'on réitère une infinité de fois.

Il est temps de comprendre ce qui s'est passé au niveau des aires, c'est-à-dire du point de vue des nombres qui permettent de mesurer l'aire du carré et les aires coloriées.

Les étapes sont faciles à décrire de proche en proche. Le carré initial mesure $36~\textrm{cm}^2$. Lors de la première découpe, le carré rouge, le vert et le bleu mesurent donc $\displaystyle \frac{36}{4}~\textrm{cm}^2$ chacun. Au passage, on remarque ici que ce nombre est bien sympathique et ne nécessite aucun détour par l'infini : $\displaystyle \frac{36}{4}=9$ ! Chaque carré mesure à cette étape $9~\textrm{cm}^2$, et en regroupant les 4 on obtient bien les $36~\textrm{cm}^2$ de départ.

À la seconde étape, on a des petits carrés, qui mesurent cette fois-ci $\displaystyle \frac{36}{16}~\textrm{cm}^2$. Comment le sait-on ? Le carré de départ mesure $36~\textrm{cm}^2$, à l'étape suivante chaque carré mesure le quart, $9~\textrm{cm}^2$, ensuite le quart de l'un de ces carrés, $\displaystyle \frac{9}{4}$, ou $\displaystyle \frac{36}{4\times 4}$, etc.

On peut prédire la suite : le petit carré blanc sera coupé en 4 carrés d'aire $\displaystyle \frac{36}{4\times 4 \times 4}=\displaystyle \frac{36}{4^3}$ (on est à l'étape 3), puis le petit carré blanc restant en 4 carrés d'aire $ \displaystyle \frac{36}{4^4}$, etc.

Il nous reste à mesurer l'aire coloriée en bleu, rouge ou vert, au choix, car c'est la même !

Additionnons donc les aires des carrés verts, par exemple : $\displaystyle \frac{36}{4}+\displaystyle \frac{36}{4^2}+\frac{36}{4^3}+\cdots$

Comme cela ne s'arrête jamais, les mathématiciens ont inventé une notation bien pratique pour désigner ce calcul1 : $$\displaystyle \sum_{i=1}^\infty\frac{36}{4^i} = \frac{36}{4}+\frac{36}{4^2}+\frac{36}{4^3}+\cdots$$

Mais revenons maintenant à une réalité plus concrète : au final, on a bien réparti notre carré initial en 3 parties égales, en utilisant des quarts de quarts de quarts, etc. Si l'on écrit cela en termes de nombres et de mesures d'aires, on a donc : $$\displaystyle \sum_{i=1}^\infty\frac{36}{4^i} = \frac{36}{3}= 12.$$

Une somme de quart, de quart de quart, de quart de quart de quart, etc. à l'infini donne un tiers ! Voila donc qu'un tiers peut être vu comme composé d'une infinité de quarts. Une façon de réconcilier deux nombre rationnels qui, écrits sous forme décimale, ne semblaient pas partager grand chose.

Pour finir, et mieux se rendre compte de l'efficacité des représentations des nombres et des sommes infinies que nous avons introduits, regardons notre calcul $\displaystyle \sum_{i=1}^\infty\frac{36}{4^i}$ en écriture décimale. Pour y parvenir observons que le lien entre les fractions $\displaystyle \frac{36}{4^i}$ écrites sous forme décimale n'est pas si évident : $\displaystyle \frac{1}{4}=0,25$, $\displaystyle \frac{1}{4^2}=0,0625$, $\displaystyle \frac{1}{4^3}=0,015625$, $\displaystyle \frac{1}{4^4}=0,00390625$, $\dots$ , $\displaystyle \frac{1}{4^{10}}=0,00000095367431640625$, $\dots$

Il ne reste plus qu'à tout multiplier par 36 et additionner ces nombres $\dots$ jusqu'à l'infini ! Ce qui rend assez sympathique les notations que les mathématiciens utilisent pour ne pas s'encombrer de ces très longues suites de décimales.

Bien sûr, nous sommes partis avec un carré de côté mesurant $6~\textrm{cm}$, car l'aire est alors $36~\textrm{cm}^2$ qui se divise facilement par 4 à la première étape. On aurait aussi, comme souvent en mathématiques, partir avec un carré de coté unitaire, c'est-à-dire de coté mesurant $1$ unité. On aurait alors obtenu : $$\displaystyle \sum_{i=1}^\infty\frac{1}{4^i} = \frac{1}{3}.$$