Les mouvements browniens sont des objets mathématiques qui permettent de modéliser des phénomènes aléatoires, notamment physiques et financiers. Ce sont aussi de puissants outils pour développer certains domaines mathématiques.
Introduction
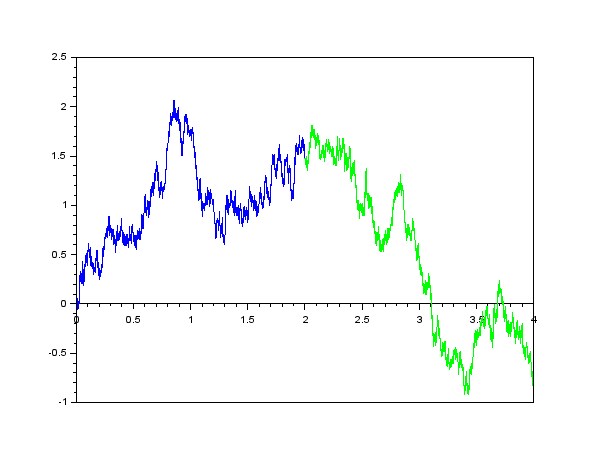
Historiquement, les mouvements browniens ont été mis en avant en 1827 par le biologiste Robert Brown lors de l'observation de particules larges de quelques microns extraites de l'intérieur de grains de pollen. Déposées dans une mince couche de liquide au repos sur une lame de microscope, Brown a remarqué que, non seulement ces particules se déplaçaient mais qu'en plus leurs trajectoires semblaient erratiques (voir la figure 1 pour une simulation d'une trajectoire possible). Ce phénomène est en fait dû aux chocs aléatoires des molécules composant le liquide contre la particule observée.
En 1923, Norbert Wiener développe alors un modèle mathématique cohérent avec ces observations et qui est à la base de toute une branche des probabilités : le calcul stochastique.
Dans ce qui suit nous allons introduire ce modèle mathématique que nous nommerons donc mouvement brownien et ce en plusieurs dimensions. Nous nous intéresserons ensuite à ce que l'on nomme un couplage de mouvements browniens ainsi qu'à quelques applications en découlant.
Caractérisation du mouvement brownien en dimension 1
C'est le type de trajectoire que l'on pourrait observer si notre particule de pollen ne pouvait se déplacer que le long d'un fil infini et gradué. On se fixe un point de départ $x$ le long de ce fil.
Le mouvement brownien est la donnée de la fonction continue $B:t\mapsto B(t)$ où $B(t)$ est la position prise par la particule au temps $t\geq 0$ le long du fil gradué. C'est ce qu'on appelle un processus aléatoire : pour tout temps $t$ la valeur $B(t)$ est aléatoire. (Dans le langage probabiliste, $B(t)$ est une variable aléatoire). Dans le cas où notre mouvement brownien part de la valeur $x$ (c'est-à-dire $B(0)=x$), $B(t)$ suit une loi bien connue des probabilistes et statisticiens puisqu'elle permet l'étude de nombreux phénomènes naturels : la loi normale $\mathcal{N}(x,t)$ d'espérance $x$ et de variance $t$.
Le mouvement brownien, quelle que soit sa valeur de départ, est caractérisé par deux propriétés provenant des observations du phénomène physique. Nous allons les expliquer grâce aux figures ci-dessous (figures 2 et 3). Ces deux figures représentent une trajectoire possible pour un mouvement brownien partant de $0$ en fonction du temps qui passe. Évidemment, cette trajectoire est aléatoire : si on refaisait une simulation de ce mouvement brownien partant de $0$, on obtiendrait un autre tracé.
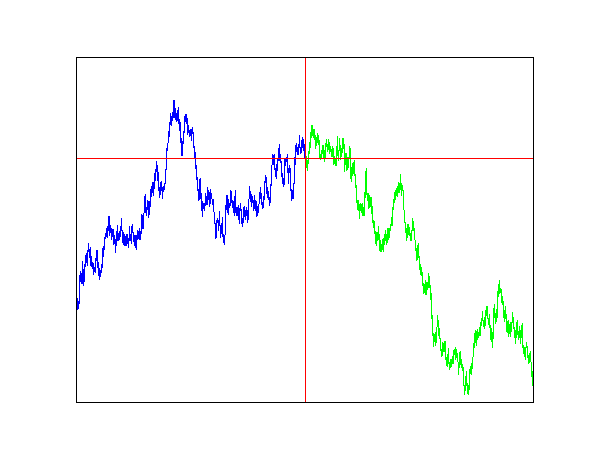
Fixons un temps $t_0$. Sur les figures nous prendrons $t_0=2$ pour l'exemple.
Propriété
(Figure 2)La trajectoire du mouvement brownien après le temps $t_0$ (tracée en vert) ne dépend que de sa valeur au temps présent $t_0$ et non pas du passé de la trajectoire avant le temps $t_0$ (tracée en bleu). Plus généralement, on dit que les accroissements du mouvement brownien sont indépendants.
Propriété
(Figure 3)Si l'on re-fixe l'origine de notre repère gradué au point $(t_0,B(t_0))$, tracer la suite de notre trajectoire revient à recommencer à tracer un mouvement brownien à partir de ce nouveau point de départ. Plus généralement, on dit que les accroissements du mouvement brownien sont stationnaires1.
Notons que le mouvement brownien partant de $0$ vérifie une propriété de symétrie :
Propriété
(Symétrie)Soit $B$ un mouvement brownien partant de $0$, alors le processus aléatoire opposé $-B:t\mapsto -B(t)$ est aussi un mouvement brownien partant de $0$.1
En général, si on veut construire un mouvement brownien partant d'une valeur réelle $x$, on construit un mouvement brownien partant de $0$ noté $B(t)$ et on regarde $B_x(t)=x+B(t)$.
En dimension 1, le mouvement brownien vérifie une propriété très intéressante:
Propriété
(Temps d'atteinte)
Le mouvement brownien, quel que soit son point de départ, atteint n'importe quelle valeur réelle en un temps fini avec probabilité $1$, c'est-à-dire presque sûrement.1
Ainsi, en reprenant notre analogie avec l'expérience de Brown, une particule de pollen passera presque sûrement par tous les points du fil et ce autant de fois qu'on le souhaite. Il faut garder en tête que le temps mis par le mouvement brownien pour atteindre une valeur fixée est lui-même aléatoire. De plus, on connait sa loi de probabilité1. En particulier, si l'on nomme $a$ la valeur à atteindre et si le point de départ considéré est $0$, on peut montrer que la probabilité que le mouvement brownien atteigne pour la première fois cette valeur après l'instant $t$ est inférieure à $\dfrac{2|a|}{\sqrt{2\pi t}}$. Remarquons que cette relation n'est pertinente que pour $t$ suffisamment grand.
Dans la pratique, le mouvement brownien en dimension 1 permet de modéliser et donc d'étudier l'évolution de placements financiers.
Étude en dimension 2
Intéressons-nous désormais au mouvement brownien en dimension supérieure, par exemple dans le plan (dimension 2). C'est cet exemple qui est proposé en introduction.
Fixons un repère orthonormé dans le plan. On peut alors définir le mouvement brownien grâce à deux mouvements browniens réels $B^1$ et $B^2$ indépendants l'un de l'autre (ils n'influent pas l'un sur l'autre). La trajectoire horizontale du mouvement brownien sera donnée par $B^1$ (c'est la première coordonnée) et la trajectoire verticale sera donnée par $B^2$ (seconde coordonnée). On peut alors noter $B:t\mapsto B(t)=\begin{pmatrix} B^1(t) \\ B^2(t) \end{pmatrix}$ le mouvement brownien en dimension 2.
Le mouvement brownien peut être défini de façon similaire en dimension 3 (dans l'espace). On peut alors s'en servir pour modéliser des molécules de gaz par exemple.
Il est à noter que, si l'on choisit un point du plan, le mouvement brownien en dimension 2 pourra passer aussi près que l'on veut de ce point sans jamais l'atteindre et ce presque sûrement.
Couplages
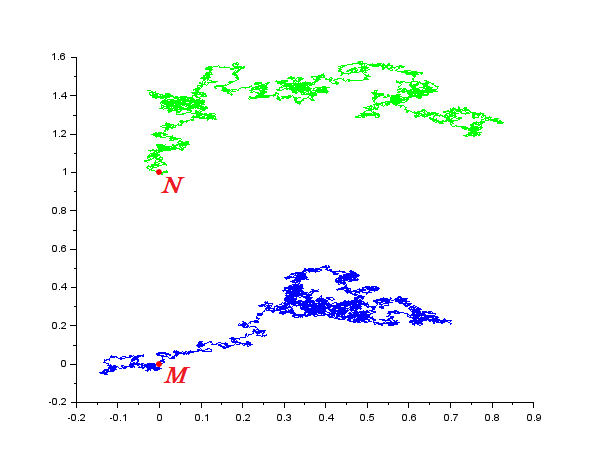
Comme expliqué précédemment, les mouvements browniens permettent de modéliser et donc de mieux comprendre certains phénomènes physiques. Par exemple, étudions le comportement des particules de pollen observées dans une mince couche d'eau sur des lames de microscopes. On se place donc en dimension 2. Notons une partie de cette surface aqueuse (par exemple un disque). On s'intéresse à la question suivante : comment le point de départ de notre particule de pollen, noté $M$, va-t-il influer sur le temps pris pour atteindre le disque $\mathcal{D}$ ?
Pour cela imaginons un autre point dans le plan, noté $N$, peut être plus proche ou plus éloigné du disque $\mathcal{D}$, et fixons un temps $t$. La particule de pollen a-t-elle beaucoup plus ou beaucoup moins de chance d'être dans le disque $\mathcal{D}$ en ce temps fixé en partant de $M$ ou de $N$ ? Peut-on quantifier cette différence de probabilités ?
Pour répondre à cette question nous allons utiliser ce qu'on appelle un couplage.
Introduction aux couplages de mouvements browniens
Le couplage de mouvements browniens consiste à définir deux mouvements browniens, partant éventuellement de deux points différents, en prenant en compte la manière dont ils vont influer l'un sur l'autre ou pas. On a par exemple vu en dimension 1 qu'à partir d'un mouvement brownien $B$ partant de $0$, on pouvait créer un second mouvement brownien $-B$ partant de $0$. $-B$ dépend évidemment de $B$ mais il a bien la dynamique aléatoire d'un mouvement brownien : $(B,-B)$ forme alors un couplage.
Dans ce qui suit nous allons parcourir trois exemples de couplages parmi les plus utilisés en dimension 2.
- Une première façon d'effectuer un couplage consiste à les prendre totalement indépendants l'un de l'autre : les mouvements browniens n'influent pas l'un sur l'autre.
- Une autre façon consiste à considérer qu'ils ont les mêmes trajectoires aux points de départ près, c'est-à-dire à une translation près. C'est ce qu'on appelle le couplage synchrone : en particulier les mouvements browniens restent à la même distance l'un de l'autre au cours du temps.
- Une troisième façon consiste à définir les mouvements browniens de façon à ce qu'ils soient symétriques l'un par rapport à l'autre jusqu'à leur point de rencontre. À partir du point de rencontre, les mouvements browniens seront choisis égaux.
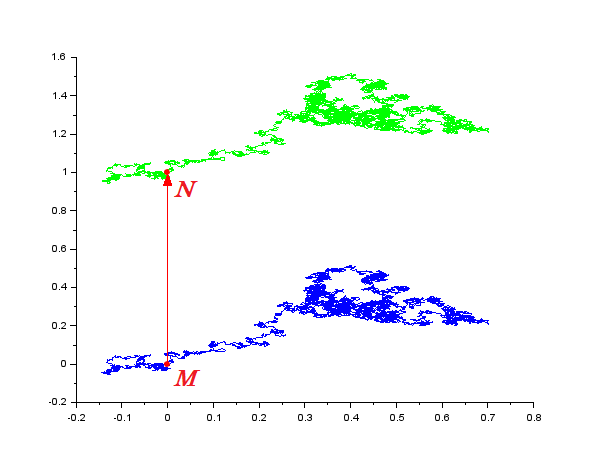
Par exemple, dans le plan : notons respectivement $M$ et $N$ les points de départ de nos mouvements browniens. On commence par tracer la médiatrice au segment $[MN]$. On définit ensuite $B_N$, le mouvement brownien partant de $N$, simultanément à $B_M$, le mouvement brownien partant de $M$, de façon à ce que leurs trajectoires soient symétriques par rapport à la médiatrice. On agit ainsi jusqu'au premier point de rencontre : pour la suite du couplage, on prendra $B_N$ égal à $B_M$. Notons que, par définition, ce premier temps de rencontre est le premier temps d'atteinte de la médiatrice. Ce couplage est appelé couplage miroir ou couplage par réflexion.
Il est bien sûr essentiel de vérifier que la trajectoire tracée par symétrie est bien celle d'un mouvement brownien. Cela se montre très bien cependant grâce à la propriété de symétrie du mouvement brownien citée précédemment (propriété 3)1.
Il est intéressant de remarquer que nos deux mouvements browniens se rencontrent presque sûrement. En effet, comme expliqué précédemment, en dimension 2, le mouvement brownien partant de $M$ va se rapprocher autant qu'on le souhaite de n'importe quel point du plan : il va donc en particulier finir par atteindre la région située de l'autre côté de la médiatrice par rapport au point de départ. Par continuité, il va alors (presque sûrement) toucher la médiatrice. Au premier instant où la médiatrice est atteinte, les deux mouvements browniens se rencontrent.
Pour le couplage miroir, on est même capable d'estimer le premier temps de rencontre puisque, avant cette rencontre, la moitié de la distance entre les browniens $\dfrac{d(B_M(t),B_N(t))}{2}$ a en fait elle-même le comportement d'un troisième mouvement brownien réel (de dimension 1) cette fois2. Nous le noterons $C(t)$. Savoir à quel moment $B_M$ et $B_N$ se rencontrent, revient donc à savoir quand leur distance est nulle et donc quand le mouvement brownien $C$ atteint $0$. C'est quelque chose que les probabilistes peuvent calculer et même estimer avec des fonctions simples comme expliqué en partie 2 (voir la propriété 4). Ainsi la probabilité que les mouvements browniens $B_M$ et $B_N$ se rencontrent après le temps $t$ est inférieure à $\dfrac{d(M,N)}{\sqrt{2\pi t}}\cdot$
Application à notre problème
Revenons à notre étude des particules de pollen : la particule a-t-elle beaucoup plus, beaucoup moins de chance d'être dans le disque $\mathcal{D}$ au temps fixé $t$ en partant de $M$ ou de $N$ ? Qu'en est-il à long terme, c'est-à-dire pour un temps $t$ grand ?
Pour répondre à cette question, on va étudier ici la différence de probabilités $|P(B_M(t)\in \mathcal{D})-P(B_N(t)\in \mathcal{D})|$ où $B_M$ et $B_N$ sont des mouvements browniens partant respectivement de $M$ et de $N$ modélisant chacun une particule de pollen.
La valeur $P(B_M(t)\in \mathcal{D})$ intervenant ici ne dépend pas du choix du couplage puisqu'on ne regarde à chaque fois que la dynamique aléatoire de la particule de pollen partant de $M$. Il en est de même pour $P(B_N(t)\in \mathcal{D})$. On peut donc choisir n'importe quel couplage $(B_M,B_N)$. Ici, on prendra le couplage miroir. L'utilisation de ce couplage implique que les particules de pollen modélisées se rencontrent presque sûrement en un temps fini et qu'une fois qu'elle se sont rencontrées, elles restent confondues.
L'évènement $\{B_M(t)\in D\}$ ("la particule de pollen partant de $M$ est dans le disque au temps $t$") peut alors s'éxprimer comme l'union de deux évènements incompatibles :
- "La particule de pollen est dans le disque au temps $t$ ET les deux particules de pollen sont confondues au temps $t$", c'est à dire $\{B_M(t)\in \mathcal{D}$ et $B_M(t)=B_N(t)\}$;
OU
- "La particule de pollen est dans le disque au temps $t$ ET les deux particules de pollen ne sont pas confondues au temps $t$", c'est à dire $\{B_M(t)\in \mathcal{D}$ et $B_M(t)\neq B_N(t)\}$.
En passant aux probabilités, on obtient : $$\begin{equation*}P(B_M(t)\in \mathcal{D})=P[B_M(t)\in \mathcal{D} \text{ et } B_M(t)=B_N(t)]+P[B_M(t)\in\mathcal{D} \text{ et } B_M(t)\neq B_N(t)].\end{equation*}$$
En faisant la même décomposition avec $B_N(t)$, on obtient : $$\begin{equation*}P(B_N(t)\in \mathcal{D})=P[B_N(t)\in \mathcal{D} \text{ et } B_M(t)=B_N(t)]+P[B_N(t)\in\mathcal{D} \text{ et } B_M(t)\neq B_N(t)] \end{equation*}$$
On peut alors montrer que :
$|P(B_M(t)\in \mathcal{D})-P(B_N(t)\in \mathcal{D})|\leq 2P(B_M(t)\neq B_N(t))\leq 2 P(\tau>t)$ où $\tau$ est le premier temps de rencontre pour le couplage miroir.
Grâce aux connaissances sur le temps de rencontre des mouvements browniens dans le cas du couplage miroir, on obtient finalement $|P(B_M(t)\in \mathcal{D})-P(B_N(t)\in \mathcal{D})|\leq 2\dfrac{d(M,N)}{\sqrt{2\pi t}}$.
En particulier, on peut voir que, plus $t$ est grand, plus les deux probabilités sont proches : au bout d'un certain temps, le point de départ n'a plus beaucoup d'impact sur le fait d'atteindre $\mathcal{D}$ et plus généralement sur la trajectoire de la particule de pollen.
Conclusion
Outre l'étude de certains phénomènes de nature aléatoire, le mouvement brownien permet de mieux comprendre les phénomènes de diffusion (d'une épidémie, de la chaleur dans un matériau...). Ces phénomènes vérifient des équations faisant intervenir un objet mathématique appelé laplacien. Pour aller plus loin, en fixant $n$ un entier, le laplacien d'une fonction $f:\mathbb{R}^n\mapsto \mathbb{R}$ au point $x\in\mathbb{R}^n$, noté $\Delta f(x)$ peut alors être obtenu en étudiant la loi de probabilité de $f(B_x(t))$ où $B_x(t)$ est un mouvement brownien défini sur $\mathbb{R}^n$ et partant de $x$1. Les couplages de mouvements browniens, au travers d'inégalités comme celles obtenues dans la partie 4.2., permettent alors de mieux comprendre le laplacien.
En définissant le mouvement brownien sur des espaces à la géométrie particulière comme la sphère, le plan hyperbolique ou même certains espaces de matrices, on peut aussi obtenir des résultats pour des phénomènes de diffusion évoluant dans ces espaces pourvu qu'on arrive à y définir des couplages satisfaisants comme dans le plan.