VITE, la version cotée de la formule de Bayes est disponible ici ! Ainsi que ses applications aux tests dans le domaine médical, ou au filtrage anti-spam de votre courrier électronique...
Cet article est consacré à la formule de Bayes, plus précisément dans sa version « cotée », enseignée chez les Anglo-Saxons 1 et qui nous paraît plus fonctionnelle. Après en avoir rappelé le principe, s'ensuivent quelques applications dans les domaines du test médical et du filtrage anti-spam : des thématiques figurant aujourd'hui dans les programmes scolaires français 2.
Qu'on se le dise : il y aura ici des équations. Mais elles seront abondamment illustrées et mobiliseront surtout des connaissances de lycée — aussi bien en mathématiques qu'en enseignement scientifique ou en sciences numériques (SNT et NSI). Ce texte pourra donc servir aux futurs bacheliers préparant leur grand oral de terminale et désireux d'approfondissements, sous la supervision de leurs professeurs.
Introduction (a priori)
Qui n’a jamais vécu l’une de ces soirées électorales sans suspense, au favori désigné par les sondages, dont la victoire annoncée se précise au fil du dépouillement, à mesure que les bureaux de vote dévoilent leurs résultats ? À l’inverse, qui ne se souvient pas le cœur encore vibrant d’émotion, d’une rencontre sportive dont l’outsider, but après but, mètre après mètre, seconde après seconde, vient déjouer tous les pronostics, retournant progressivement le cours des événements ?
Voici condensés dans ces anecdotes les grands principes de l’inférence bayésienne, la « formule du savoir » comme on aime à l’appeler 1 :
-
choix d’une hypothèse ou d’une croyance assortie, d’entrée, d’un certain niveau de confiance a priori ;
-
prise d’une à plusieurs informations successives ;
-
révision(s) dans un sens comme dans l’autre a posteriori de son premier jugement jusqu’à confirmation éventuelle.
Il y a là une dimension philosophique à ces concepts que nous « mathématiserons » : une quête de vérité, certes, mais dont au bout du chemin n’émergera qu’une probabilité, donc la possibilité, même mince, que tout puisse advenir.
Donner ainsi des clés de compréhension du monde interroge nécessairement la formation du citoyen. C’est logiquement que les nouveaux programmes de lycée ménagent une part belle aux probabilités. Pourtant, elles furent longtemps réduites à un entrefilet (Figure 1) et ce n’est qu’à la faveur des « mathématiques modernes » qu’une place significative leur est accordée pour la première fois.
Extrait du programme de Philosophie-Sciences (devenue Sciences-Ex en 1945, puis la série D en 1967). Le paragraphe dédié aux probabilités tient en cette seule phrase.
Aussi, la notion de conditionnement est-elle abordée à partir de 1971, d’abord en série littéraire (Figure 2), mais pas avant 1991 dans les filières scientifiques (Figure 3) !
Programme complémentaire de probabilités de la série littéraire Terminale A. Les programmes complémentaires en probabilités des terminales scientifiques C, D et E ne mentionnent pas le conditionnement.
Programme de Terminale C (extrait).
Deux notations auront cohabité, comme on le lit sur les programmes de l’époque. L’écriture historique \({\mathbb{P}}_B(A)\), celle de Kolmogorov (1933), père des probabilités modernes ; et l’écriture \({\mathbb{P}}(A \mid B)\), aujourd’hui la plus répandue dans la littérature. Les deux désignent bien entendu le même quotient,
\[{\mathbb{P}}_B(A)={\mathbb{P}}(A \mid B)=\frac{{\mathbb{P}}(A\cap B)}{{\mathbb{P}}(B)},\]
défini lorsque le facteur de normalisation \(\mathbb{P}(B)\) est non nul. La notation \({\mathbb{P}}(A \mid B)\) suit l’ordre de la pensée — pour « \(A\) sachant \(B\) » ; mais a le défaut de laisser croire que « \(A \mid B\) » est un événement. La notation \({\mathbb{P}}_B(A)\) est plus lourde à employer, en particulier lors de plusieurs conditionnements successifs ; mais elle rappelle bien que \({\mathbb{P}}_B(\bullet) ={\mathbb{P}}(\bullet \mid B)\) est une probabilité, une mesure de l’événement \(A\), la focale braquée sur \(B\). Tout ce qui sort du périmètre de \(B\) n’est plus comptabilisé dans la probabilité de \(A\), c’est un « effet de loupe ».
Programme de mathématiques complémentaires en Terminale (extrait)
Il faudra encore patienter jusqu’au programme de la rentrée…2020 (Figure 4) pour que la formule de Bayes (Figure 5) soit à l’honneur, ainsi que sa mise en œuvre à travers l’étude des causes par leurs effets. On y fait le lien entre \({\mathbb{P}}_B(A)\) et \({\mathbb{P}}_A(B)\), où les événements \(A\) et \(B\) sont tour à tour observables ou observés. Désormais, les probabilités imprègnent tous les curriculums français. Pas de doute, elles ont la cote…et comme nous le verrons, elles le rendent bien !
Le texte, publié en 1763 à titre posthume 1, préfigure la loi de succession du marquis de Laplace 2. Il est d'un abord triplement difficile. Il est écrit en vieil anglais, où certains « s » ont l'apparence d'un « f ». Il utilise un langage géométrique, les intégrales étant des portions d'aire d'un carré ABCD. Enfin, son objectif très particulier n'est pas simple à cerner : il s'agit d'identifier a posteriori le paramètre d'une loi binomiale, paramètre qu'on suppose a priori équidistribué sur $[0,1]$, sachant qu'ont été observés $p$ succès contre $q$ échecs.
De la formule de Bayes à la formule des cotes
La mécanique de la formule de Bayes exploite une observation \(e\) (de l’anglais evidence au sens d’« élément de preuve ») afin de préciser la pertinence d’une hypothèse \(H\) (comme Hypothesis). La recevabilité de \(H\) se mesure par une probabilité a priori, \({\mathbb{P}}(H)\), qui, éclairée de l’événement \(e\), est a posteriori rajustée en \({\mathbb{P}}(H \mid e)\). La correction peut s’exercer à la hausse ou à la baisse, consolidant ou fragilisant ainsi la foi en l’hypothèse \(H\).
Les contextes d’application sont très divers. En médecine 1, le sujet est un patient, l’hypothèse \(H\) une maladie, l’alarme \(e\) est un syndrome ou la réaction manifeste à un test. En sécurité informatique 2, l’objet d’étude peut être un courriel qui, au regard d’un ou plusieurs critères \(e\) constatés en réception (un mot clé dans le corps du message, une taille atypique, l’absence d’objet, le format d’un fichier joint, une alerte sur un bit de contrôle, etc.) est possiblement suspect — ce qui constitue l’hypothèse \(H\). En matière de justice pénale, \(H\) peut être l’innocence de l’accusé, \(e\) un fait constaté par la police. De nombreux débats ont eu lieu sur de possibles erreurs judiciaires qui auraient pu être évitées par une application correcte de la formule de Bayes 3.
La méthode la plus courte pour établir la formule de Bayes consiste à enchaîner les égalités
\begin{equation} \mathbb{P} ( H \mid e ) \times \mathbb{P} (e) = \mathbb{P} (H \cap e) = \mathbb{P} (e \cap H) = \mathbb{P} (e \mid H ) \times \mathbb{P} (H) \label{preformuleBayes} \end{equation}
Dès lors, quand $\mathbb{P}(e) \neq 0$ et $\mathbb{P}(H) \neq 0,$
\begin{equation}
\underbrace{\mathbb P\left(H \mid e\right)}_{\text{probabilité}\;\textit{a posteriori}} \;=\; \underbrace{\frac{\mathbb P\left(e \mid H\right)}{\mathbb P(e)}}_{\text{coefficient bayésien}} \;\times\;\underbrace{ \mathbb P(H)}_{\text{probabilité}\;\textit{a priori}} \label{formuleBayes}
\end{equation}
La probabilité « inversée » \({\mathbb{P}}\left(e \mid H\right)\) s’appelle une vraisemblance, ou une probabilité de transition car elle indique dans quelle proportion l’hypothèse \(H\), une fois fondée, se traduirait par l’observation \(e\). En appliquant l’équation \eqref{formuleBayes}, la probabilité a priori \({\mathbb{P}}(H)\), à droite, se trouve ré-évaluée a posteriori en \({\mathbb{P}}\left(H \mid e\right)\), à gauche.
Il arrive souvent que la probabilité \({\mathbb{P}}(e)\) figurant au dénominateur du coefficient bayésien en \eqref{formuleBayes} ne soit pas connue au préalable. On la reconstitue en moyennant des probabilités conditionnelles via la formule des probabilités totales. Cela mène à une expression plus touffue :
\begin{equation}\mathbb{P}(H \mid e) = \frac{\mathbb{P}(e \mid H) \mathbb{P}(H)}{\mathbb{P}(e \mid H) \mathbb{P}(H)+\mathbb{P}(e \mid \overline{\!H}) \mathbb{P}(\,\overline{\!H})} \label{formuleBayesBis}\end{equation}
Cette version « scolaire » de la formule de Bayes n’est pas pratique. Dans le second membre, \({\mathbb{P}}(H)\) intervient tant au numérateur qu’au dénominateur. On ne peut pas prédire à « vue d’œil », sans faire tout le calcul, dans quel sens évoluera la probabilité de \(H\). Or les algorithmes de complétion d’un navigateur Web ou GPS brassent des données massives auxquelles ils agrègent en temps réel quantité d’observations \(e\) (géolocalisation, historique des recherches, premiers mots constituant la requête, choix des utilisateurs de profil similaire, etc.). Ces algorithmes ont besoin de routines efficaces, qui anticipent rapidement une tendance, même grossière, estimant les chances d’un événement \(H\) qu’untel demande tel renseignement ou veuille aller à tel endroit. Dans ce but, ils manipulent des cotes de confiance (odds en anglais), un concept que l’on rencontre aussi dans les paris sportifs. Pour ce faire, on élimine le terme parasite \({\mathbb{P}}(e)\) qui apparaît dans l’équation \eqref{preformuleBayes} en la rapportant à sa relation duale, portant sur \(\overline{\!H}\) au lieu de \(H\),
\begin{equation}{\mathbb{P}}\big(\overline{\!H} \mid e\big) \,\times\, {\mathbb{P}}(e) = {\mathbb{P}}\big(e \mid \overline{\!H}\big) \, \times \, {\mathbb{P}}(\overline{\!H}). \label{formuleBayesDuale}\end{equation}
La division de \eqref{preformuleBayes} par \eqref{formuleBayesDuale} conduit à la formule, dite des cotes :
\begin{equation}
\underbrace{\frac{\mathbb P\left(H \mid e\right)}{\mathbb P\big(\overline{H} \mid e\big)}}_{\text{cote}\;\textit{a posteriori}\;\text{de}\;H} = \underbrace{\frac{\mathbb P\left(e \mid H\right)}{\mathbb P\big(e \mid \overline{H}\big)}}_{\text{rapport de vraisemblance}}\;\times\; \underbrace{\frac{\mathbb P(H)}{\mathbb P\big(\overline{H}\big)}}_{\text{cote}\;\textit{a priori}\;\text{de}\;H}
\label{formuleCotes}
\end{equation}
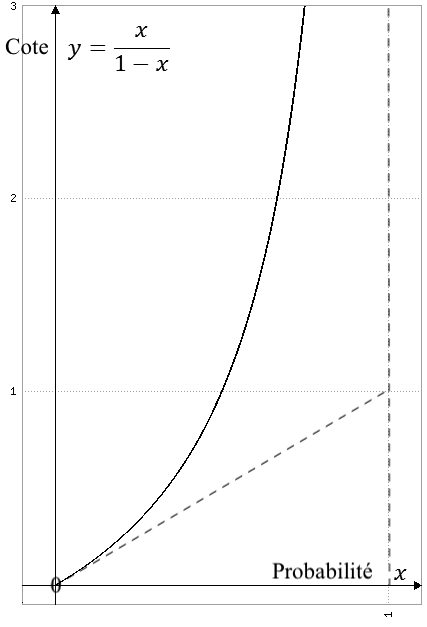
Graphe de la fonction $y=f(x)$, sa tangente à l'origine et son asymptote en pointillés.
La cote de \(H\) met en rapport l’éventualité de \(H\) à son alternative \(\overline{\!H}\) — que cette cote soit a priori, c’est-à-dire non conditionnée à \(e\), ou a posteriori, c’est-à-dire conditionnée à \(e\). Comme \({\mathbb{P}}(\overline{\!H}) = 1 - {\mathbb{P}}(H)\) et \({\mathbb{P}}(\overline{\!H} \mid e) = 1 - {\mathbb{P}}(H \mid e)\), les cotes a priori et a posteriori de \(H\) sont les images par la fonction
\[f(P)= \frac{P}{1-P}\]
des probabilités a priori et a posteriori. La fonction \(f\) définit une bijection croissante de \([0,1]\) sur \([0,+\infty]\) (Figure 6). Ainsi dans l’équation \eqref{formuleCotes}, la cote de \(H\) passe de \(f({\mathbb{P}}(H) )\) à \(f({\mathbb{P}}(H \mid e) )\). Si elle augmente (respectivement, diminue), c’est que sa probabilité, qui elle passe de \({\mathbb{P}}(H)\) à \({\mathbb{P}}(H \mid e)\), a augmenté (ou diminué).
Le quotient
\[ \frac{\mathbb{P}(e \mid H )}{\mathbb{P} (e \mid \overline{\!H} )} \]
rapporte deux vraisemblances, d’où son nom rapport de vraisemblance (Likelihood Ratio, en abrégé \(\sf{LR}\) en anglais). Comparé à $1$, il détermine s’il est plus vraisemblable d’observer \(e\) sous l’hypothèse \(H\) ou sous son complémentaire \(\overline{\!H}\) — et par ricochet, si la probabilité de \(H\) doit être relevée ou diminuée. Quand il vaut $1$, c’est-à-dire aussi quand \({\mathbb{P}}(e \mid H) + \mathbb{P}(\overline{e} \mid \overline{\!H}) = 1 \) la probabilité de \(H\) reste inchangée. Concrètes et précieuses, ces informations nous arrivent désormais d’un seul regard.
Retenons donc que la formule des cotes \eqref{formuleCotes} remplace utilement la formule de Bayes \eqref{formuleBayesBis}. La relation non linéaire en \( \mathbb{P}(H) \) est ainsi remplacée par une simple homothétie, impliquant certes une image déformée de \(H\) (sa cote), mais de loin plus lisible.
Dans la suite, nous appliquerons la formule des cotes aux tests médicaux (uniques d’abord, puis répétés jusqu’à confirmation), ainsi qu’à la détection des pourriels (spams) où elle s’avère indispensable. En effet, contrairement à la formule de Bayes qui engendre de l’instabilité numérique1, la formule des cotes, grâce à sa structure multiplicative, pourra remarquablement s’itérer sans difficulté à mesure que remontent les observations \(e\), \(e'\), \(e''\), etc.
Un petit point technique : les formules \eqref{formuleBayesBis} et \eqref{formuleCotes} montrent que tout s’imbrique ; cotes a priori, a posteriori et vraisemblances, chacune est liée à toutes les autres ! Pour éviter de s’égarer dans ces circonvolutions, on postulera en général que les probabilités de transition
\[\mathbb{P}(e \mid H), \;\, \mathbb{P}(\overline{e} \mid H), \;\, \mathbb{P}(e \mid \overline{\!H})\;\, \text{et} \;\, \mathbb{P}(\overline{e} \mid \overline{\!H})\]
ne dépendent pas de la valeur de \({\mathbb{P}}(H)\). Ceci sera clarifié dans les parties suivantes, mais notons d’ores et déjà que cela ne va pas de soi. Si, par exemple, nous prenons pour \(H\) : « tomber d’une échelle » et pour \(e\) : « se casser la jambe », on doit accepter que \({\mathbb{P}}(e\mid H)\) soit peu sensible à la fréquence des chutes. Cela est plausible — dans certaines limites car plus on tombe, plus on apprend à tomber.
Interlude : conditionnement vs causalité
Marquons une courte pause, le temps de distinguer conditionnement et causalité, car l’occasion s’y prête. Nous avons vu que la donnée de l’événement \(e\) est de nature à modifier la probabilité de l’hypothèse \(H\). Si correction il y a, cela ne veut pas dire que l’événement \(e\) influe sur l’état \(H\), mais plutôt qu’il influe sur la probabilité que \(H\) survienne. La nuance est importante.
Songeons à la météorologie, phénomène aléatoire par excellence. Soit l’hypothèse \(H\) : « il pleut » un jour donné sur Paris, symboliquement représenté par $\large{\text{?}}$ ; et soit \(e\) le fait qu’un certain Parisien ait sorti son parapluie, noté $\large{\text{☂}}$. Les événements $\large{\text{?}}$ et $\large{\text{☂}}$ sont naturellement solidaires, chacun des deux se reflétant dans l’autre : que l’un se produise et la probabilité que l’autre se réalise aussi grimpe en flèche. S’il pleut, il y a de bonnes chances que l’habitant en question, s’il n’a pas oublié son parapluie, s’en serve. Réciproquement, s’il s’en sert c’est raisonnablement qu’il pleut. Malgré ce caractère mutuel, seul $\large{\text{?}}$ s’interprète comme une cause de $\large{\text{☂}}$.
Si maintenant nous suivons également le comportement d’un deuxième Parisien, vivant dans un autre quartier de sorte qu’ils ne se concertent ni ne se rencontrent. Ce deuxième habitant peut, le même jour, avoir ouvert son parapluie, ${\large{☂}'}$ ou pas. Inévitablement, les états $\large{\text{☂}}$ et ${\large{☂}'}$ s’intriquent : le lien logique qui unit $\large{\text{☂}}$ et ${\large{☂}'}$ est de l’ordre de l’implication (et même de l’équivalence), avec cependant une dose d’incertitude. Mais ce lien n’est pas de l’ordre de la cause à l’effet, la cause étant extérieure. Il faut se représenter une bifurcation, où $\large{\text{?}}$ suscite $\large{\text{☂}}$ et, indépendamment, ${\large{☂}'}$. Nous y reviendrons plus loin, au § 4.6 au moment d’itérer des tests médicaux.
C’est grave docteur ?
Un peu de vocabulaire
Le milieu médical a développé son propre vocabulaire dans les domaines du dépistage ou du diagnostic :
- L’hypothèse \(H\) ou \(M\) concerne l’état de santé d’un patient vis-à-vis d’une maladie donnée (typiquement, une infection virale), noté \(M\) pour « malade » — c’est-à-dire porteur de cette maladie, et son complémentaire \(\overline{\!M}\) pour « sain » — c’est-à-dire non porteur de cette maladie ;
- L’événement \(e\) ou \(t\) annonce un « test positif », son complémentaire \(\overline{t}\) un test « négatif », réactions du patient à un test calibré pour la maladie donnée ;
- La prévalence désigne la probabilité a priori \(p=\mathbb{P}(M)\), assimilée à la concentration de malades (de la pathologie étudiée) dans la population ciblée, dont le patient est extrait ;
- La valeur prédictive positive (VPP) est la probabilité a posteriori \(\mathbb{P}(M \mid t)\) d’être malade (de la pathologie étudiée) quand le test est positif. En contrepoint, la valeur prédictive négative (VPN) donne celle a posteriori \(\mathbb{P}(\overline{\!M} \mid \overline{t})\) d’être sain quand le test est négatif ;
- La sensibilité et la spécificité sont des probabilités de transition, respectivement \(s_e = \mathbb{P}(t \mid M)\) et \(s_p = \mathbb{P}(\overline{t} \mid \overline{\!M})\). Elles signent la capacité de discernement du test : son aptitude à déceler l’infection (en y étant sensible), et cette infection seulement (elle lui est spécifique). Déduit d’un échantillon statistique lors des essais cliniques, le couple \((s_e ; s_p)\) est ensuite affiné grâce aux retours du terrain. On le considérera stabilisé, intrinsèque au test, donc indifférent au profil des individus désormais prélevés. Cette clause est évidemment discutable, comme cela a été fait en fin de § 2;
- Les vrais positifs ($\,VP\,$) sont les malades (\(\,M\,\)) dont le test est positif (\(t\)), les vrais négatifs ($\,VN\,$) les individus sains (\(\, {\overline{\!M}}\, \)) au test négatif (\(\overline{t}\)), les faux positifs ($\,FP\,$) les individus sains (\(\, \overline{\!M}\,\)) au test positif (\(t\)), les faux négatifs ($\,FN\,$) les malades (\(\, M\, \)) au test négatif (\(\overline{t}\)).
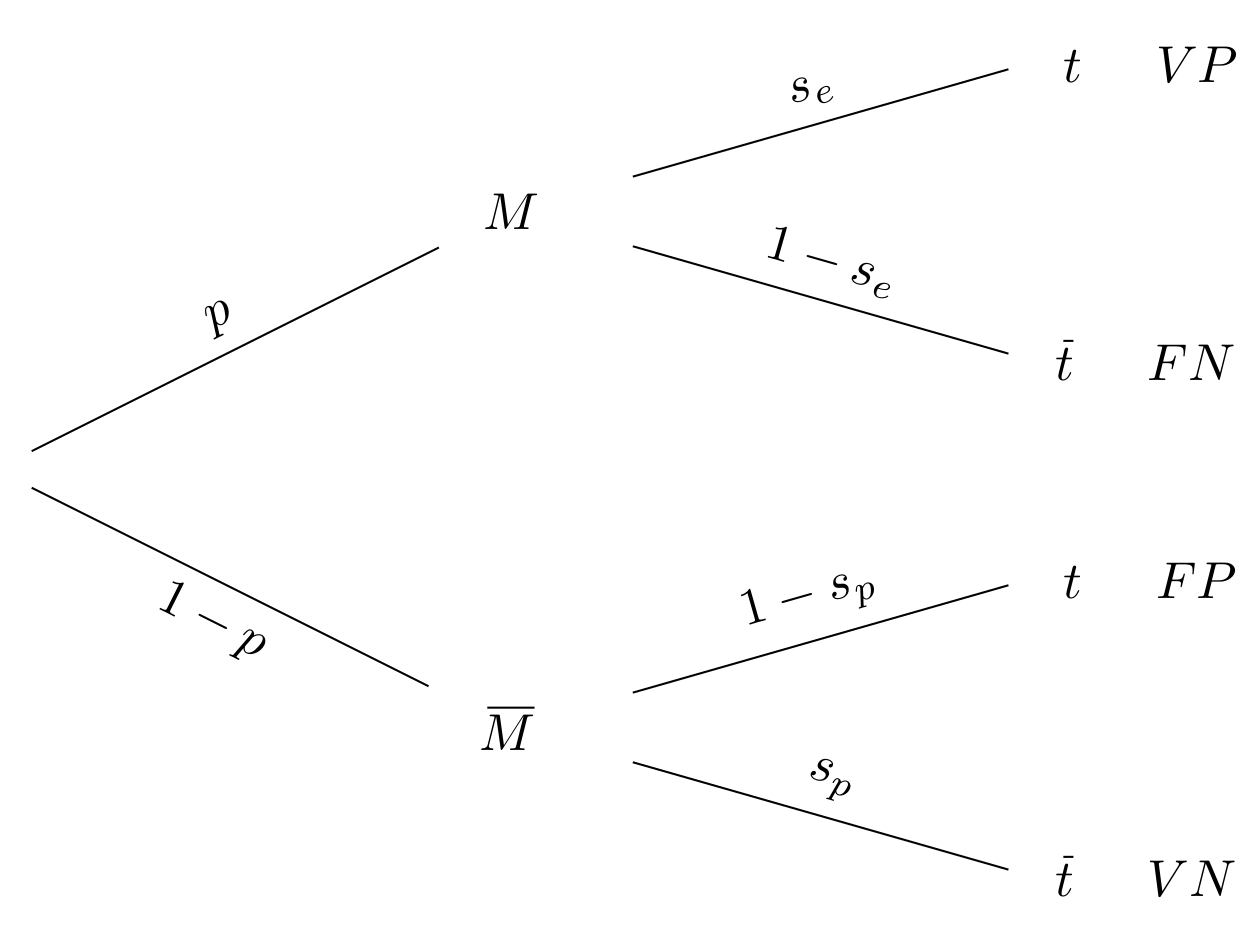
Tables, arbres et robinets
On a coutume en classe de tout résumer par une table à double entrée (Figure 7 ci-après)
| \(\overline{\!M}\) | \(M\) | Total | |
|---|---|---|---|
| \(\overline{t}\) | \(s_p (1-p)\) | \((1-s_e) p\) | \(s_p (1-p) + (1-s_e) p\) |
| \(t\) | \((1-s_p)(1-p)\) | \(s_e p\) | \((1-s_p)(1-p)+s_e p\) |
| Total | \(1-p\) | \(p\) | \(1\) |
ou sur un arbre pondéré (Figure 8 ci-dessous).
La table a été normalisée : l’effectif total y est ramené à l’unité, qui peut être la centaine, le millier, le million etc. d’individus. On peut ainsi la lire en termes de loi conjointe, celle du couple test–santé, ou en tant que tableau de contingence. En diagonale, on repère les vrais positifs (en recoupant \(t\) et \(M\)) et les vrais négatifs (\(\overline{t}\) et \(\overline{\!M}\)) ; faux négatifs (\(\overline{t}\) et \(M\)) et faux positifs (\(t\) et \(\overline{\!M}\)) se trouvant en regard.
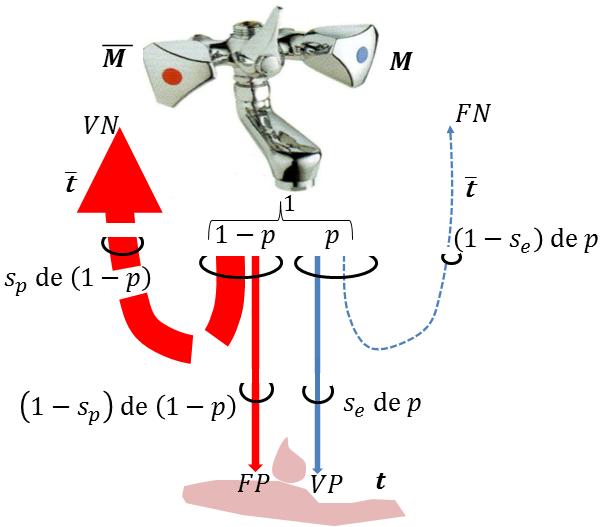
L’arbre déploie ses ramifications, chacune étant surmontée de la probabilité d’être empruntée une fois qu’on s’y est hissé. Les trajets rectilignes aboutissent aux vrais positifs ou aux vrais négatifs, les aiguillages aux faux négatifs ou aux faux positifs. Structurée, cette représentation se prête à la répétition des expériences (pour étudier deux, trois, quatre, etc. patients), et facilite la modélisation sur ordinateur du problème posé. Cependant, elle en éclipse pour partie le sens. Pour l’apprécier, il faudrait épaissir à leurs justes proportions et recourber des branches de l’arbre de la figure 8, comme en figure 9 qui compare la population à une masse d’eau.
Le mitigeur, disons celui d’un hammam, délivre l’eau au débit normalisé à l’unité. Il dose une quantité \(p\) d’eau froide, du fait d’une petite fuite, correspondant à l’état \(M\) (pour « Main droite »), et la quantité \(\overline{p}=1-p\) d’eau très chaude pour l’état \(\overline{\!M}\) (« \(\overline{\text{M}}\)ain gauche »). Idéalement, \(p=0\) et \(1-p=1\). Les arêtes deviennent des canaux (imaginaires), aux diamètres appropriés. Côté droit, une fraction \(s_e\) (proche de $1$) va à la terre (\(t\)), tandis que la portion \(1-s_e\) s’évapore (\(\overline{t}\)). Symétriquement, il s’évapore une fraction \(s_p\) (tendant vers $1$ en conditions extrêmes), diffusée dans l’air, et le reste coule au sol. Aux probabilités de transition usuelles correspondent des transitions ou non de phase, entre liquide et gaz. Recueillons une gouttelette à terre. Elle est associée à l’événement \(t\). Remonter à sa source la plus probable consiste à confronter la probabilité \(\mathbb{P}(M \mid t)\) qu’elle provienne du robinet d’eau froide à sa probabilité complémentaire, \(\mathbb{P}(\overline{\!M} \mid t)\), qu’elle provienne du robinet d’eau très chaude.
L’arbitrage n’est pas si clair, comme on le verra dans le « paradoxe du diagnostic » au § 4.5. En effet, les deux filets d’eau sont parfois semblables. Peu d’eau froide coule car, bien qu’elle se déverse pour l’essentiel à terre, on peut penser que la fuite est minime. Beaucoup d’eau très chaude est propulsée ; certes elle part surtout en vapeur, mais il y en a tant que la partie qui finit à terre rivalise en quantité avec l’eau froide.
Formules pour un test unique
La formule de Bayes dérive quant à elle de notre analogie sans aucun calcul et d’une simple « pesée ». Ainsi, le mélange qui va globalement à terre (il s’agit de l’observation \(t\)) est composé du volume \(s_e p\) d’eau froide et du volume \((1-s_p)(1-p)\) d’eau très chaude. Donc,
\[\mathbb{P}(M\mid t) = \frac{s_e p }{s_e p +(1-s_p)(1-p)}\]
Les volumes étant rapportés à l’unité, nous obtenons bien \eqref{formuleBayesBis}, à savoir
\begin{equation}\mathbb{P}(M\mid t) = \frac{s_e \mathbb{P}(M)}{s_e \mathbb{P}(M) +(1-s_p)(1-\mathbb{P}(M))} \label{formuleBayesTest}\end{equation}
Toutefois, comme expliqué au § 2, nous lui préférons son équivalent coté adapté de \eqref{formuleCotes} plus compact :
\begin{equation} \frac{\mathbb{P}(M \mid t)}{1-\mathbb{P}(M \mid t)} = \frac{s_e}{1-s_p} \times \frac{\mathbb{P}(M)}{1-\mathbb{P}(M)} \label{formuleCotesTest} \end{equation}
Le rapport de vraisemblance
\[{\sf{LR}} = \frac{s_e}{1-s_p}\]
n’a plus qu’à être comparé à $1.$ Remis dans un contexte médical, quand \(\sf{LR}\) est supérieur à $1,$ un test positif accentue la suspicion de pathologie. Inférieur à $1,$ il l’atténue. Égal à $1,$ lorsque \(s_e+s_p =1\), il ne la change pas.
Diagrammes de Venn
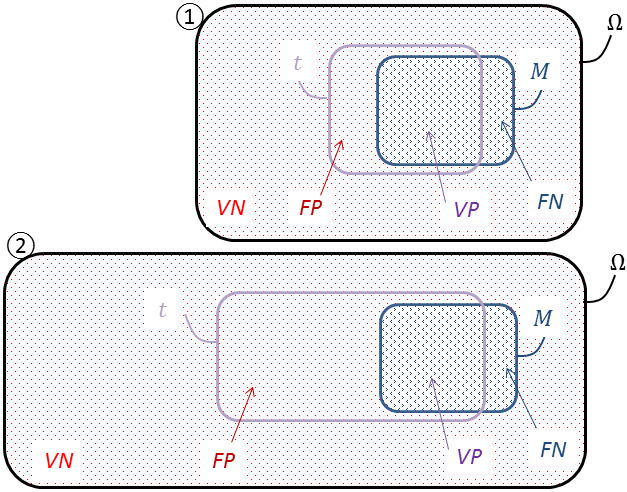
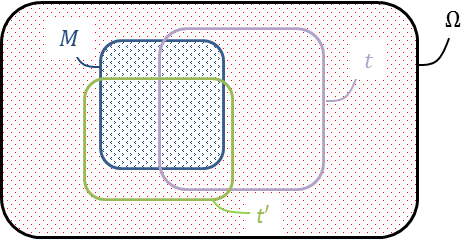
Mieux que la représentation arborescente, les diagrammes de Venn 1 rendent visuellement bien la nature ensembliste des probabilités (Figure 10) telle qu’elle fut axiomatisée par Kolmogorov 2.
L’univers \(\Omega\) renferme ici toute une population, matérialisée par les nombreux points comme autant d’individus la composant, malades ou non, réactifs ou pas. C’est une immense urne dans laquelle on pioche. Par commodité, les catégories qu’elle abrite ont été regroupées sur le dessin, plutôt que dispersées. On jauge ainsi mieux leurs poids relatifs, mais il est convenu qu’un individu sera tiré au sort, à l’aveugle.
Les contours de \(M\) et de \(t\) ne s’épousant pas, ils délimitent quatre régions : les zones externe et interne pour les vrais positifs $VP$ (le sous-ensemble \(M \cap t\)) et les vrais négatifs $VN$ (correspondant à \(\overline{\!M} \cap \overline{t}\)), et, comme un flou aux interstices, les faux positifs $FP$ (correspondant à \(\overline{\!M} \cap t\)) et les faux négatifs $FN$ (correspondant à \(M \cap \overline{t}\)). Ces deux dernières franges trahissent les imperfections du test.
Selon son paramétrage, un test peut gagner sur l’un des deux flancs $FP$ ou $FN,$ mais perd automatiquement sur l’autre. Ainsi, résultant de choix ou de compromis, la conception d’un test renvoie au « dilemme du magistrat » : trop sévère, la cour condamne des innocents, pas assez elle libère des coupables.
Schématiquement, on pourrait distinguer deux situations :
- Type « Covid » Une maladie très contagieuse et exceptionnellement dangereuse. Une stratégie possible consiste à confiner temporairement tous les porteurs, au risque d’en isoler qui ne le sont pas. Le dépistage des asymptomatiques doit alors être massif et sensible à $100\,\%$. Dans ce cas, un individu testé négatif serait, à coup sûr, sain, et le test est alors dit rule out ;
- Type « Cancer » Une maladie dont l’évolution est assez lente et le traitement est lourd ou provoque des effets secondaires sérieux. Mieux vaut parfois attendre un peu avant de prendre une décision, possiblement irréversible. Le diagnostic de gravité doit être spécifique à $100\,\%$. Pour ce faire les tests peuvent être complétés d'échographies ou de prélèvement histologiques par exemple. L'analyse est dite rule in. Sur un tout autre registre, on peut la rapprocher du « contrôle anti dopage » où l’individu testé positif serait, à coup sûr, tricheur, et ne serait pas disqualifié sur le champ « pour rien ».
Rappelons que nous tenons pour définitives les caractéristiques \(s_e\) et \(s_p\). Par contre, nous pourrions faire varier la prévalence \({\mathbb{P}}(M)\). Essayons de la diminuer en ajoutant (par la pensée) des individus sains à la population initiale, comme on ferait une « dilution » (Figure 10, passage de ① à ②). Le nombre de malades demeure inchangé, donc celui des vrais positifs $VP$ et celui des faux négatifs $FN$ aussi. En revanche, les vrais négatifs $VN$ et les faux positifs $FP$ augmentent, proportionnellement à la croissance de \(\overline{\!M} = \Omega\backslash M\). Or la prévalence est souvent modeste, et ne fera que baisser dans notre expérience. Les malades étant très minoritaires, \(\Omega\backslash M \approx \Omega\). Si bien que $VN$ et $FP$ augmentent presque à raison de la croissance de \(\Omega\). En particulier, si $FP$ grossit beaucoup tandis que $VP$ reste fixe, alors parmi les positifs, les faux pourraient bien supplanter les vrais. Cette remarque éclairera, elle aussi, le « paradoxe du diagnostic » ci-après au § 4.5.
Quand on répète les expériences (pour étudier deux, trois, quatre, etc. patients), les diagrammes de Venn s’avèrent moins pratiques que les arbres : il faudrait alors croiser au sens du produit cartésien (et surtout ne pas accoler au sens de l’union !).
Exemple numérique et « paradoxe du diagnostic »
Considérons une maladie (fictive) dont la prévalence est de $1\,{\large{‰}},$ testée avec une sensibilité \(s_e\) de $98\,\%$ et une spécificité \(s_p\) de $99\,\%$, soit un rapport de vraisemblance \({\sf{LR}}\), très supérieur à $1,$ de
\[{\sf{LR}}=\frac{s_e}{1-s_p} = \frac{0,98}{1-0,99}\,=\,98\]
Un individu sur $1\,000$ en souffre a priori, soit une cote de $1$ contre $999.$ S’il est testé positif, celle-ci grimpe à $98$ contre $999,$ soit une probabilité a posteriori (ou valeur prédictive positive, VPP) de \( \raise{2pt}{98}/\lower{2pt}{1\,097} \simeq 8,9\,\%\). C’est certes très supérieur à $1\,{\large{‰}},$ environ \(\mathrm{LR}\) fois plus : normal, car la prévalence étant dérisoire, la formule des cotes \eqref{formuleCotesTest} opère au voisinage de l’origine, donc sur sa plage linéaire où \(f(x) \simeq x\).
Cependant, précisément parce que la prévalence était dérisoire, cette probabilité a posteriori de \(8,9\,\%\) paraît étonnamment faible et, en même temps, rassurante pour le patient ; nous allons y revenir. Signalons d’abord qu’à l’inverse, lorsque le test est négatif, on calcule une valeur prédictive négative (VPN) en adaptant \eqref{formuleCotesTest} :
\[\frac{{\mathbb{P}}\big(\overline{\!M} \mid \overline{t}\big)}{1-{\mathbb{P}}\big(\overline{\!M} \mid \overline{t}\big)} = \frac{s_p}{1-s_e}\;\times\; \frac{{\mathbb{P}}\big(\overline{\!M}\big)}{1-{\mathbb{P}}\big(\overline{\!M}\big)}\]
L’individu présente a priori $999$ chances sur $1\,000$ d’être sain, soit une cote de $999$ contre $1$ en faveur de \(\overline{\!M}\). La cote a posteriori est $49,5$ fois supérieure. Finalement, \({\mathbb{P}}(\overline{\!M} \mid \overline{t}) \simeq 99,998\,\%\). En voilà une bonne nouvelle !
Revenons maintenant au score intrigant de $8,9\,%$ trouvé lorsque le test est positif. Pour fixer les idées, prenons une population comptant $10\,000$ individus, et remplissons un tableau croisé d’effectifs. Renseignons-y les cases en dénormalisant la table en Figure 7. Les résultats présentés sur la table en Figure 11 (et arrondis) valident le taux obtenu puisque \(\raise{2pt}{10}/\lower{2pt}{110} \simeq 9\,\%\) (de même qu’ils confirment la valeur prédictive négative calculée).
| \(\overline{\!M}\) | \(M\) | Total | |
|---|---|---|---|
| \(\overline{t}\) | \(9\,890\) | \(0\) | \(9\,890\) |
| \(t\) | \(100\) | \(10\) | \(110\) |
| Total | \(9\,990\) | \(10\) | \(10\,000\) |
Mettons-nous à la place du patient positif : sa première réaction à un test aussi fiable (\(s_e = 0,98\, ; \,s_p = 0,99\)) est de se croire malade à « $98$ malchances sur $100$ ». La seconde, découvrant qu’il ne l’est qu’au risque de $8,9\%$ seulement, oscille entre surprise et soulagement. Et pour cause, la majorité des positifs sont en bonne santé : quelque $10$ malades contre $100$ bien portants dans le tableau en Figure 11. Ceci nous explique pourquoi, sauf raison particulière, les tests systématiques sont rarement pratiqués : ils inquiètent à tort les faux positifs, engorgent les hôpitaux, engagent des traitements inutiles...
L’explication du « paradoxe » est donc fort simple : à très faible prévalence, tout se passe comme si l’on ouvrait grand le croisillon d’eau brûlante dans la figure 9, ou qu’on diluait beaucoup \(\Omega\) en étirant loin sa frontière de gauche dans la Figure 10-②.
C’est la confusion classique entre probabilité a posteriori \({\mathbb{P}}(M\mid t)\) et vraisemblance \({\mathbb{P}}(t\mid M)\) qui trouble notre intuition. Un peu comme on mélangerait un théorème et sa réciproque, ou sa gauche et sa droite. Quelques contre-exemples, tantôt récréatifs ou plus sérieux, invitent à davantage de vigilance. Florilège :
- La plupart des Français meurent dans un lit : pour autant, s’y coucher chaque soir n’est pas dangereux !
- $100\%$ des gagnants ont tenté leur chance : le fameux slogan du loto. Mais jouer n’est pas gagner ! Sur la grille, il y a $5$ numéros à cocher parmi $49,$ plus un numéro chance sur $10$ dans un petit encart. Soit une possibilité parmi \(\binom{49}{5} \times 10 = 19\,068\,840\) de partager le jackpot, bien maigre ;
- Speed dating hommes-femmes : après une rencontre-minute de célibataires comme en organisent tant les sites de rencontre, des couples se forment... parfois. La probabilité d’être un homme ($\large{♂}$) sachant qu’on y a trouvé l’amour (\( \heartsuit \)), une « maladie » comme une autre dit-on, est de \(\raise{2pt}{1}/\lower{2pt}{2}\). Pour autant, \(\mathbb{P}(\heartsuit \mid {\large{♂}}) \neq \mathbb{P}({\large{♂}} \mid \heartsuit )\). On devine que \(\mathbb{P}(\heartsuit \mid {\large{♂}})\) peut dépendre de la prévalence \(\mathbb{P}(\heartsuit)\) ainsi que de la mixité, que mesure \(\mathbb{P}({\large{♂}})\) (ou \(\mathbb{P}({\large{♀ }})=1-\mathbb{P}({\large{♂}})\)).
La langue française n’est pas étrangère à ces contresens. Souple, elle permet toujours d’énoncer \({\mathbb{P}}(t \mid M)\) en commençant à sa guise par \(M\) ou par \(t\) : probabilité que « \(t\) soit sensible à \(M\) », que « \(M\) soit révélée par \(t\) », voire que « \(t\) ait révélé \(M\) ». Il est donc plus sage de s’en tenir à la formulation plus épurée d’un « sachant que », ou à la rigueur d’un sommaire « quand » ou « si », même si derniers peuvent induire comme une concomitance.
Le test de confirmation
Prudemment, eu égard au paradoxe qu’on vient d’évoquer, un individu testé positif est habituellement re-testé, pour confirmation, un peu comme on ferait appel d’un procès. Le dépistage du VIH fonctionne sur ce modèle : un test sérologique Elisa (Enzyme-linked immunosorbent assay) comme premier filtre suivi, le cas échéant, d’un test Western Blot (du nom, déformé, de son inventeur) après une nouvelle prise de sang. En préalable à ces deux tests, un test dit d'« orientation rapide » peut même parfois avoir été réalisé.
Dans un monde parfait, on pratiquerait d’abord un test rule out (tout négatif est assurément sain, le doute subsistant uniquement aux positifs). Ce test circonscrit les malades à l’intérieur d’un premier groupe de positifs. Puis on appliquerait à ce groupe un test rule in (tout positif est assurément malade). Les positifs restants correspondent exactement aux malades. Sur le papier, l’idée n’est pas mauvaise. Elle se heurte cependant à la réalité : de tels tests n’existent pas et, pour diverses raisons, il n’est pas toujours judicieux de tester toute une population.
Le principe de la méthode retenue est exposé en détail et illustré ici sur l’exemple numérique du § 4.5 où \(s_e = 0,98\) et \(s_p = 0,99\) non seulement pour le premier test, mais aussi pour le deuxième. Après leur premier test, les sujets déclarés positifs sont réorientés vers un spécialiste de l’infection suspectée. Le flux des patients qui lui arrivent ne sont pas contaminés au taux de $1$ pour $1\,000$ (cote de $1$ contre $999$), mais à celui de $8,9$ pour cent (cote de $98$ contre $999$). Ce praticien conduit son propre diagnostic, dont l’issue sera positive (\(t'\)) ou négative (\(\overline{t'}\)). Pour l’exploiter, l’ancienne probabilité a posteriori, celle là même que ses confrères obtenaient, va servir de nouvelle probabilité a priori, donc de nouvelle prévalence. En substituant \(t'\) à \(t\) dans la formule \eqref{formuleCotesTest}, et en y remplaçant \({\mathbb{P}}(\,\bullet\,)\) par la probabilité conditionnelle \({\mathbb{P}}_t(\,\bullet\,) = {\mathbb{P}}(\bullet\mid\,t)\), on aboutit d’abord à
\begin{equation}\frac{{\mathbb{P}}(M \mid t'\cap t)}{1-{\mathbb{P}}(M \mid t' \cap t)} = \frac{{\mathbb{P}}(t' \mid M \cap t)}{{\mathbb{P}}(t' \mid \overline{\!M} \cap t)}\times \frac{\mathbb{P}(M \mid t)}{1-{\mathbb{P}}(M \mid t)} \label{equationIntermediaire}\end{equation}
Ceux qui sont familiers des conditionnements multiples auront vu la notation plus synthétique \({\mathbb{P}}(A \mid B,C,\ldots)\) au lieu de \({\mathbb{P}}(A \mid B\cap C \cap \ldots)\). Attention, on n’écrit par contre jamais \(A\mid B \mid C \mid \ldots\) car comme déjà signalé en introduction, \(A \mid B\) n’est pas un événement : il n’y a jamais qu’une seule barre « \(|\) » de conditionnement, tout ce qui se trouve à sa gauche se réfère aux événements dont on mesure la probabilité, et tout ce qui se trouve à sa droite se réfère aux événements qui définissent le périmètre connu. Ceux que les conditionnements multiples rebutent pourront toujours obtenir \eqref{equationIntermediaire} en contournant notre raisonnement, par « la force brute ». Pour cela, il faut ré-exprimer chaque probabilité conditionnelle comme par exemple
\[\mathbb{P}(M \mid t'\cap t) = \frac{\mathbb{P}(M\cap t' \cap t)}{\mathbb{P}(t' \cap t)}\]
et télescoper les fractions dans le produit du second membre.
Bien entendu, les événements \(t\) et son complémentaire \(\overline{t}\) d’un côté, et \(t'\) et son complémentaire \(\overline{t'}\) de l’autre sont intimement liés. Mathématiquement, ils sont (très) dépendants. Mais les examens biologiques sont anonymés, dirigés par des équipes différentes utilisant leurs procédés et matériels. On peut ainsi comparer \(t\) et \(t'\) aux actions ${\large{☂}}$ et ${\large{☂}'}$, et \(M\) et \( \overline{\!M} \) aux deux visages du temps ${\large{?}}$ et $\overline{{\large{?}}}$ du § 3. Connaître lequel des statuts \(M\) ou \( \overline{\!M} \) prévaut conditionne les probabilités de \(t\) et \(t'\). Mais savoir, en plus, que l’événement \(t\) s’est produit, n’orientera pas davantage la probabilité de \(t'\) et vice versa.
Ainsi, bien que dépendants a priori, \(t\) et \(t'\) sont indépendants a posteriori. Autrement dit, ils sont indépendants sous les hypothèses conditionnelles \(M\) et \(\overline{\!M}\). En clair,
\[\mathbb{P}(t'\mid t) \neq \mathbb{P}(t') \; \text{mais}\; \mathbb{P}(t'\mid t\cap M) = \mathbb{P}(t'\mid M)\;\text{et}\; \mathbb{P}(t'\mid t\cap\overline{M}) = \mathbb{P}(t'\mid \overline{M})\]
On marque traditionnellement l’indépendance de deux événements par la notation $\bullet ⫫ \bullet$ et l'indépendance de deux événements conditionnellement à l'hypothèse $H$ par la notation $\bullet ⫫ \bullet \mid H$. Aussi écririons-nous, synthétiquement :
\[t' \mathrel{\not{\!⫫}} t \;\;\; \text{mais} \;\;\; t' ⫫ t\ \mid M \;\;\; \text{et} \;\;\; t' ⫫ t\ \mid \overline{\!M}\]
Bien sûr, les positions de \(t\) et \(t'\) autour du symbole $⫫$ sont sans importance : il y a symétrie. Représenter avec réalisme \(t\) et \(t'\) sur un croquis, en restituant toutes les contraintes, n’est pas si facile.
Le diagramme en Figure 12 garantit l’indépendance de \(t\) et \(t'\) conditionnellement à \(M\), puisqu’à l’évidence \(\mathbb{P}(t'\mid t\cap M)=\mathbb{P}(t' \mid M) \simeq \raise{2pt}{2}/\lower{2pt}{3}\) quand on rapporte la surface de \(t'\cap t\cap M\) à celle de \(t\cap M\), puis la surface de \(t'\cap M\) à celle de \(M\). L’indépendance de \(t\) et \(t'\) conditionnellement à \(\overline{\!M}\) est moins frappante sur le dessin, et plus approximative (l’indépendance passe automatiquement au complémentaire côté événements, pas côté condition !).
Moyennant quoi, puisque \(t' ⫫ t \mid M\),
\[\mathbb{P}(t' \mid t\cap M) = \mathbb{P}(t' \mid M) = s_e'\]
et, puisque \(t' ⫫ t\ \mid \overline{\!M}\),
\[\mathbb{P}(t' \mid t \cap\overline{\!M}) = \mathbb{P}(t' \mid \overline{\!M}) = 1-s_p'\]
En procédant soigneusement, les formules des cotes s’agencent alors en
\begin{equation}\frac{\mathbb{P}(M \mid t'\cap t)}{1-\mathbb{P}(M \mid t' \cap t)} = \frac{s_e'}{1-s_p'} \frac{s_e}{1-s_p} \frac{\mathbb{P}(M)}{1-\mathbb{P}(M)}\end{equation}
Le résultat est miraculeux : on actualise en deux étapes la cote de \(M\). Autrement dit, en conjuguant les deux tests, on en multiplie les rapports de vraisemblance :
\[\sf{LR}_{t',t} = \sf{LR}_{t'}\times \sf{LR}_{t}\]
Lorsque \((s_e' ; s_p') = (s_e ; s_p) = (0,98 ; 0,99)\), la cote bondit ainsi d’un facteur $98$ élevé au carré en cas de double positif. Soit, avec \({\mathbb{P}}(M) = 1\), \({\mathbb{P}}(M \mid t) \simeq 8,9\,\%\) et \({\mathbb{P}}(M \mid t'\cap t) \simeq 90,5\,\%\). Là oui, c’est grave docteur.
Spam, Spam, Spam and Spam
Ce qu’on appelle communément spam (« pourriel » en français) tire son origine du jambon précuit en boîte (Spiced Ham, ou spam) via un sketch des Monty Python où le spam pollue la conversation et le menu d’un restaurant (Figure 13). Personne ne l’aime, mais il nous envahit en nous interrompant constamment. Comment lutter ?
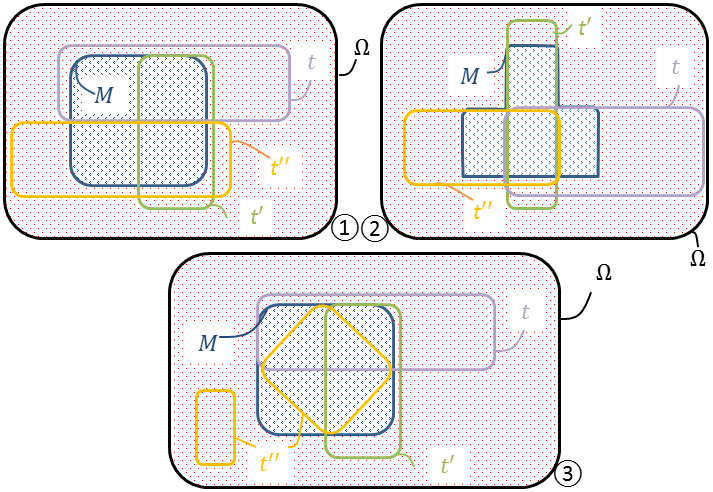
La démarche et les notations exposées au § 4.6 s’étendent à plus de deux tests, sous réserve qu’ils soient mutuellement indépendants quand ils sont subordonnés aux hypothèses \(M\) et \(\overline{\!M}\). Ce cadre est tout théorique. Il faut d’ailleurs tâtonner avant de s’en faire une image mentale, qu’aident à former les esquisses de la Figure 14.
On y a progressivement pour trois tests \(t\), \(t'\), \(t''\) :
- ① \(t ⫫ t' \mid M\) ; \(t' ⫫ t'' \mid M\) mais \(t'' \mathrel{\not \!{⫫}} t \mid M\). En effet, \(\mathbb{P}(t' \mid t\cap M) = \mathbb{P}(t' \mid M) ( = \raise{2pt}{1}/\lower{2pt}{2}) \) tout comme \(\mathbb{P}(t'' \mid t'\cap M) = \mathbb{P}(t'' \mid M)\) mais \(\mathbb{P}(t'' \mid t\cap M) = 0\) crée une incompatibilité,
- ② \(t ⫫ t' \mid M\) ; \(t' ⫫ t'' \mid M\) et \(t'' ⫫ t \mid M\) mais \((t,t',t'')\) non mutuellement indépendants. En effet, \( \mathbb{P}(t' \mid t\cap M) = \mathbb{P}(t' \mid M) ( = \raise{2pt}{1}/\lower{2pt}{2}),\) avec des relations analogues en tournant sur les tests. Mais \(\mathbb{P}(t'' \mid t\cap t'\cap M)\), égal à $1$ (événement certain), ne peut aussi valoir \(\mathbb{P}(t'' \mid M) = \raise{2pt}{3}/\lower{2pt}{4}\),
- ③ \(t,t',t''\) mutuellement indépendants conditionnellement à \(M\). En effet, sous le couvert de \(M\), les probabilités d’un test relativement à
- aucun des deux autres tests,
- l’un quelconque des deux autres tests,
- les deux autres tests
valent invariablement \(\raise{2pt}{1}/\lower{2pt}{2}\). Par exemple,
\[{\mathbb{P}}(t\mid M) = {\mathbb{P}}(t\mid t'\cap M) = {\mathbb{P}}(t\mid t''\cap M) = {\mathbb{P}}(t\mid t'\cap t'' \cap M) = \raise{2pt}{1}/\lower{2pt}{2}\]
Toutefois, sauf à retoucher encore le croquis, les tests ne sont pas indépendants sous la condition \(\overline{\!M}\).
Si, sur le plan de la santé, on s’en tient à deux tests, d’autres domaines, tel celui de la détection des spams (?, et son contraire \(\overline{?}=?\)), vont bien au-delà. Nous l’avions mentionné en début de § 2, les filtres se fondent notamment sur tout un corpus \(\mathcal{C}\) de mots clés, susceptibles d’éveiller les soupçons et auxquels sont attribués, par un processus d’apprentissage, des vraisemblances. En vrac,
\[\mathcal{C}=\{\texttt{money},\,\texttt{sex},\,\texttt{amazing},\,\texttt{congrats},\,\texttt{credit},\,\texttt{free},\, \texttt{medicine},\,\texttt{loans}, \texttt{offer},\ldots\}\]
associé par exemple aux probabilités
\[{\mathbb{P}}(\texttt{money} \mid ?) = 0,7 \quad {\mathbb{P}}(\texttt{offer} \mid ?) = 0,5 \quad {\mathbb{P}}(\texttt{amazing} \mid ?) = 0,2 \;\ldots\]
et
\[{\mathbb{P}}(\texttt{money} \mid ?) = 0,1 \quad {\mathbb{P}}(\texttt{offer} \mid ?) = 0,01 \quad {\mathbb{P}}(\texttt{amazing} \mid ?) = 0,1 \;\ldots\]
Les termes du lexique \(\mathcal{C}\) sont dépendants a priori. Mais à l’examen des seuls spams, dont les textes sont pauvres, rarement bien construits et souvent mal traduits, il n’est pas absurde de les penser a posteriori mutuellement indépendants, à savoir indépendants sous la condition ?. La très grande variété des non-spams permet également d’espérer les mots de \(\mathcal{C}\) mutuellement indépendants sous la condition ?. L’approche est naïve, bien sûr. Appliquées à un message contenant $\texttt{money},$ $\texttt{amazing}$ et $\texttt{offer},$ les formules des cotes s’emboîtent alors en cascade jusqu’à
\[\begin{aligned} \frac{{\mathbb{P}}(? \mid \texttt{money}\cap \texttt{amazing}\cap \texttt{offer})}{{\mathbb{P}}(? \mid \texttt{money}\cap \texttt{amazing}\cap \texttt{offer})} &=\\ \frac{{\mathbb{P}}(\texttt{money} \mid ?)}{{\mathbb{P}}(\texttt{money} \mid ?)} \times \frac{{\mathbb{P}}(\texttt{amazing} \mid ?)}{{\mathbb{P}}(\texttt{amazing} \mid ?)} &\times \frac{{\mathbb{P}}(\texttt{offer} \mid ?)}{{\mathbb{P}}(\texttt{offer} \mid ?)} \times \frac{{\mathbb{P}}(?)}{{\mathbb{P}}(?)}\end{aligned}\]
Le total est comparé à un seuil. Rien n’interdit de tenir aussi compte des signaux négatifs. Si le mot $\texttt{free}$ est absent du texte, on factorise le second membre ci-dessus par le rapport de vraisemblance
\[\frac{\mathbb{P}(\overline{\texttt{free}} \mid ?)}{\mathbb{P}(\overline{\texttt{free}} \mid ?)}\]
pour mettre à jour la cote
\[\frac{\mathbb{P}(? \mid (\overline{\texttt{free}}\cap \texttt{money}\cap \texttt{amazing}\cap \texttt{offer})}{\mathbb{P}(? \mid (\overline{\texttt{free}} \cap \texttt{money}\cap \texttt{amazing}\cap \texttt{offer})}\]
Le message remonte, de ce fait, en légitimité.
De façon générale, la cote initiale \(\frac{\mathbb{P}(?)}{\mathbb{P}(?)}\) amorçant le calcul, est assez subjective. En vérité, elle importe peu tant elle est ensuite peaufinée.
Pour alléger les opérations, les produits sont transformés en sommes en prenant le logarithme — ce faisant, les \(\sf{LR}\) deviennent des \(\sf{LLR}\), pour Log Likelihood Ratios
\[\log\frac{\mathbb{P}(\overline{\texttt{free}} \mid ?)}{\mathbb{P}(\overline{\texttt{free}} \mid ?)} + \log \frac{\mathbb{P}(\texttt{money} \mid ?)}{\mathbb{P}(\texttt{money} \mid ?)} + \log \frac{{\mathbb{P}}(\texttt{amazing} \mid ?)}{{\mathbb{P}}(\texttt{amazing} \mid ?)} + \log \frac{\mathbb{P}(\texttt{offer} \mid ?)}{\mathbb{P}(\texttt{offer} \mid ?)}\]
En base $10,$ celui-ci peut être remplacé par le nombre de chiffres significatifs de l’argument auquel il s’applique, doublé d’un signe. Par exemple, \(\log(35\,456) \simeq 4\) et \(\log(0,0023) \simeq -3\). Ces astuces, quoique grossières, accélèrent l’exécution, donc la prise de décision.
Comparons finalement ces formules à celles— tout à fait équivalentes, au niveau théorique — que la classique formule de Bayes aurait délivrées. Partant de la probabilité \(\mathbb{P}(? \mid \overline{\texttt{free}}\cap \texttt{money}\cap \texttt{amazing}\cap \texttt{offer})\) on en inverse le conditionnement en exprimant le dénominateur par la formule des probabilités totales (notations abrégées pour la circonstance) :
\[\frac{\mathbb{P}(\overline{\texttt{free}}\cap \texttt{money}\cap \texttt{amazing}\cap \texttt{offer} \mid ?) \mathbb{P}(?)}{ \mathbb{P}(\overline{\texttt{f}}\cap \texttt{m}\cap \texttt{a}\cap \texttt{o}\mid ?) \mathbb{P}(?) + \mathbb{P}(\overline{\texttt{f}}\cap \texttt{m}\cap \texttt{a}\cap \texttt{o}\mid ?) \mathbb{P}(?) }\]
On invoque l’indépendance (présumée) des mots de \(\mathcal{C}\) conditionnellement à ? et conditionnellement à ?. En découle la relation à rallonge :
\begin{split}\mathbb{P}(? | \overline{\texttt{f}}\cap &\texttt{m}\cap \texttt{a}\cap \texttt{o}) = \\ & \frac{\mathbb{P}(\overline{\texttt{f}} | ?) \mathbb{P}(\texttt{m}| ?) \mathbb{P}(\texttt{a}|?) \mathbb{P}(\texttt{o}|?) \mathbb{P}(?)}{\mathbb{P}(\overline{\texttt{f}}| ?) \mathbb{P}(\texttt{m}| ?) \mathbb{P}(\texttt{a}| ?)\mathbb{P}(\texttt{o}| ?)\mathbb{P}(?) + \mathbb{P}(\overline{\texttt{f}} | ?) \mathbb{P}(\texttt{m}| ?) \mathbb{P}(\texttt{a}| ?) \mathbb{P}(\texttt{o}| ?)\mathbb{P}(?)}\end{split}
Une telle écriture possède deux inconvénients majeurs. Tout d’abord, elle ne se prête pas à récurrence : s’il arrive un nouveau mot clé dans le message balayé, il faut tout recalculer pour rafraîchir la formule. De plus, les quantités multipliées sont toutes inférieures à $1$ puisque ce sont des probabilités ; s’il y en a beaucoup, elles peuvent produire des résultats si petits qu’ils ne sont pas représentables en machine (phénomène d’underflow), engendrant de l’instabilité numérique1.
Conclusion (a posteriori)
Tout en brodant autour de la formule de Bayes, cet article aura permis de récapituler plusieurs points centraux à la théorie des probabilités — conditionnement et indépendance en tête, de les articuler aux nouveaux programmes du lycée, et d’en survoler quelques applications. Une fois ces chapitres entrouverts, et à titre d’approfondissement, on consultera par exemple 2 3 4 5 sur les probabilités générales, mais aussi 6 7 8 sur la théorie de l’information.
On pourra ainsi s’intéresser à l’entropie de Shannon 9, une notion qui quantifie l’incertitude d’un système. Le contexte du § 4 y invite. Définissons les variables aléatoires \(X\) et \(Y\), respectivement indicatrices de la santé (\(M\) ou \(\overline{\!M}\)) du patient, et de sa réaction (\(t\) ou \(\overline{t}\)) au test binaire. L’entropie \(H\) de \(X\) vaut \[H(X) = -{\mathbb{P}}(M) \log{\mathbb{P}}(M) - {\mathbb{P}}(\overline{\!M}) \log{\mathbb{P}}(\overline{\!M})\] Son entropie conditionnelle sachant \(Y\) vaut quant à elle
\[\begin{align*} H(X \mid Y) &= \mathbb{E}_Y H(X\mid Y=y) \\ &=H(X\mid t)\times{\mathbb{P}}(t)+H(X\mid \overline{t})\times {\mathbb{P}}(\overline{t})\\ &=-\left\{{\mathbb{P}}(M\mid t) \log\left({\mathbb{P}}(M\mid t)\right)+{\mathbb{P}}(\overline{\!M}\mid t) \log\left({\mathbb{P}}(\overline{\!M}\mid t)\right)\right\}\times {\mathbb{P}}(t)\\ &\quad\quad - \left\{{\mathbb{P}}(M\mid \overline{t}) \log\left({\mathbb{P}}(M\mid \overline{t})\right)+{\mathbb{P}}(\overline{\!M}\mid \overline{t}) \log\left({\mathbb{P}}(\overline{\!M}\mid \overline{t})\right)\right\}\times {\mathbb{P}}(\overline{t})\end{align*}\]
Les ouvrages que nous conseillons expliquent d’où viennent ces formules. Constatons simplement que, lorsque le degré d’information augmente, l’incertitude moyenne diminue. Sur l’exemple numérique détaillé au § 4.5, nous avons d’une part
\[H(X) = -0,001 \log(0,001)- 0,999\log(0,999) \simeq 0,0034\]
et d’autre part
\[\begin{aligned} H(X \mid Y) &\simeq -\left\{0,089 \log(0,089)+0,011 \log(0,011)\right\} \times 0,01097 \\ &\quad\quad -\left\{0,00002\log(0,00002)+0,99998 \log(0,99998)\right\} \times 0,98903\\ &\simeq 0,0013\end{aligned}\]
puisque
\begin{align*}{\mathbb{P}}(t) = \mathbb{P}(t\mid M)\mathbb{P}(M)+\mathbb{P}(t\mid\overline{M})\mathbb{P}(\overline{M}) =\\ 0,98\times 0,001 + (1-0,99)\times 0,999 = 0,01097 \end{align*}
et \(\mathbb{P}(\overline{t}) = 1 - \mathbb{P}(t)=0,98903\). D’où comme annoncé
\[H(X \mid Y) \leqslant H(X)\]
Mais il y a danger : une observation très partielle ne réduit pas toujours l’incertitude pesant sur l’hypothèse formulée ; seule l’incertitude moyenne décroît. Ainsi
\[\begin{aligned} H(X\mid t) &= -{\mathbb{P}}(M\mid t) \log\left({\mathbb{P}}(M\mid t)\right)-{\mathbb{P}}(\overline{\!M}\mid t) \log\left({\mathbb{P}}(\overline{\!M}\mid t)\right)\\ &\simeq 0,11\end{aligned}\]
implique
\[H(X\mid t) > H(X)\]
Aussi stupéfiant cela soit-il, une connaissance trop ponctuelle accroît parfois localement l’incertitude. Ainsi libellé, il s’agit d’un vrai sujet de controverse philosophique. Repensons au mitigeur de la Figure 9 qui, réglé cette fois pour avoir de l’eau tiède, laisse couler autant d’eau de chaque côté. Sachant que la goutte est prélevée au sol, remonter à sa source devient indécidable.
Pour conclure, on peut se demander pourquoi les probabilités, dont on mesure la valeur scientifique et, au-delà, la dimension intellectuelle, ont tant tardé, en France, à se faire une juste place dans les manuels scolaires. Ce alors même que les plus grands mathématiciens français contribuèrent à en poser les bases jusqu’aux théorèmes les plus avancés : ne citons que Blaise Pascal, Pierre de Fermat, Georges de Buffon, Pierre-Simon de Laplace, Émile Borel, Henri Lebesgue, et Paul Lévy.
Dans ses mémoires 10, le mathématicien français Laurent Schwartz reconnaît partager la responsabilité, avec le groupe Bourbaki, de ce retard :
Bourbaki s’est écarté des probabilités, les a rejetées, les a considérées comme non rigoureuses et, par son influence considérable, a dirigé la jeunesse hors du sentier des probabilités. Il porte une lourde responsabilité, que je partage, dans le retard de leur développement en France […]
À l’écart de l’effervescence bourbakiste, les probabilités étaient en effet reléguées au rang de mathématiques appliquées (et donc impures) – en bref une simple application de la théorie de la mesure et de l’intégrale. Une vision depuis longtemps dépassée, comme le déclarait Schwartz lui-même dans sa nécrologie de Kolmogorov 1 :
Beaucoup de gens (non probabilistes) disent : “la science des probabilités n’existe pas, c’est un cas particulier de la théorie de la mesure.” Ce n’est pas une bonne manière de voir les choses ; la probabilité commence là où le conditionnement commence, et elle donne alors une foule de résultats profonds, peu en rapport avec les résultats usuels de la théorie de la mesure […]
Nous espérons sincèrement que ce texte aura, en toute vraisemblance, contribué à augmenter a posteriori cette conviction d’une richesse profonde et lumineuse des probabilités, ne serait-ce que par l’étude du conditionnement dans un contexte d’inférence bayésienne. Oui, les probabilités ont la cote !
Remerciements
Les auteurs remercient Stéphanie Bodin (IA-IPR, académie de Nantes), Edwige Croix (Professeure, académie de Lille), et l’équipe de CultureMath (ENS Ulm) : Maxime Berger, Clément Catgolin-Cartier, Frédéric Jaëck, Florian Reverchon, Sylvain Wolf pour leurs relectures minutieuses, Maïté Deroubaix (Responsable du centre de documentation de l’IGÉSR) pour son aide dans la consultation des archives, ainsi qu'Anne Burban (IGÉSR) et Johan Yebbou (IGÉSR) pour nos nombreux échanges sur ces sujets.
Documents à télécharger
Une version PDF facile à imprimer