Garder l'équilibre avec de l'exercice, et vice versa.
Le programme de la spécialité de première générale 1 comporte un volet consacré à l'apprentissage des notations mathématiques, de la théorie des ensembles, et de la logique. Cette initiation se veut progressive et transversale aux différents chapitres traités dans l'année. On pourra aussi trouver utile d'en récapituler l'essentiel sous la forme de quelques problèmes et prolongements possibles. Outre stabiliser les connaissances sur le sujet, de tels travaux d'ouverture et de synthèse placent également l'élève dans la perspective de son Grand oral 2.
À la fois curiosité intellectuelle et petit bijou d'élégance, l'étude des « ensembles bien équilibrés » nous en offre un exemple chatoyant. En effet, on révisera ou consolidera à cette occasion plusieurs fondamentaux. Citons :
- la portée, en mathématiques, des connecteurs logiques « et » et « ou » ;
- le sens de la locution « $x\in \mathcal{E}$ », c'est-à-dire de l'appartenance d'un élément $x$ à un ensemble $\mathcal{E}$ et, le cas échéant, la possibilité donnée au mathématicien de piocher l'élément en question autant de fois qu'il le désire ;
- la notion de couple et donc, en filigrane, de produit cartésien d'ensembles ;
- l'usage raisonné des quantificateurs existentiel, « $\exists$ », et universel, « $\forall$ », soit qu'on les aura juste verbalisés, soit qu'on sera allé, par commodité, jusqu'à les symboliser (sans obligation toutefois) ;
- la négation d'une proposition, la recherche d'exemples et de contre-exemples ;
- la démarche d'un raisonnement par l'absurde ainsi que celle d'un raisonnement par équivalence;
- la différence entre le fini et l'infini ainsi qu'un avant-goût de récurrence ;
- la conception d'un algorithme itérant sur une collection d'éléments, et dans la ou les boucles duquel on prévoira une condition d'échappement au bon endroit, au bon moment.
Par ailleurs, inégalités larges comme strictes, mais aussi minima, maxima et facteurs d'échelle interviendront plus ponctuellement au cours de la résolution.
Inspiré d'un énoncé national d'Olympiades de première 3, nous en structurerons l'exposé de manière à lui donner un caractère plus linéaire. Définissons et illustrons donc sans plus attendre ce que nous entendons par un « ensemble bien équilibré» .
Définition. Exemples. Contre-exemples
Définition
(Ensemble bien équilibré)Un ensemble $\mathcal{E}$, sous ensemble de $\mathbb{R}$, est bien équilibré quand pour tout couple $(a,b)$ avec $a$ et $b$ appartenant à $\mathcal{E}$, il existe un élément $c$ de $\mathcal{E}$ tel que l'un des nombres $a$, $b$ ou $c$ est la moyenne arithmétique (ou demi-somme) des deux autres. Plus formellement : $$ \forall (a,b) \in \mathcal{E}^2,\, \exists c\in \mathcal{E},\, a=\frac{b+c}{2}\text{ ou }b=\frac{a+c}{2}\text{ ou }c=\frac{a+b}{2}. $$
On notera bien que les nombres $a$ et $b$ choisis au départ sont quelconques. En particulier, ils peuvent être égaux. Quant au potentiel nombre $c$, il n'est pas non plus nécessairement distinct des deux premiers. Rappelons-le : on peut puiser à volonté un élément dans un ensemble.
Trois exemples.
- un singleton $\mathcal{E} = \{x\}$, $x$ réel, est toujours un ensemble bien équilibré. En effet, sans autre choix possible, $a$ et $b$ se concentrent en $x$ et $c=x$ convient ;
- l'ensemble $\mathcal{E} = \{0, 1, 2\}$ est bien équilibré : $1$ est au milieu des nombres $0$ et $2$ et il s'avère que cette propriété implique les trois éléments de $\mathcal{E}$. De plus, quand $a$ et $b$ coïncident, $c=a=b$ convient ;
- l'ensemble $\mathcal{E} = \{0, \frac{2}{3}, 1, \frac{4}{3}, 2\}$ est bien équilibré. Remarquons que $1$ est milieu de $0$ et $2$, que $\frac{4}{3}$ est milieu de $\frac{2}{3}$ et $2$, que $\frac{2}{3}$ est milieu de $0$ et $\frac{4}{3}$. Ceci permet d'attribuer un $c$ convenable à n'importe quelle paire $\{a,b\}$ d'éléments distincts de $\mathcal{E}$. Bien sûr, quand $a$ et $b$ coïncident, $c=a=b$ répond toujours à l'équation.
Contre-exemples.
- une paire $\mathcal{E} = \{x,y\}$, $x$ et $y$ réels distincts, n'est jamais un ensemble bien équilibré. En effet, quand on choisit $a=x$ et $b=y$ et qu'on tente de fixer un réel $c$ en faisant tour à tour jouer à $c$, $a$ puis $b$ le rôle de milieu, on construit les éléments $c=\frac{x+y}{2}$, $c=2x-y$ et $c=2y-x$ dont aucun n'est dans $\mathcal{E}$, figure 1
- l'ensemble $\mathcal{E} = \{0, 1, 2, 3\}$ n'est pas bien équilibré. Le choix $a=0$ et $b=3$ ne permet pas d'attribuer de réponse $c$ convenable puisque ni $1,5$, ni $6$, ni $-3$ ne sont dans $\mathcal{E}$.
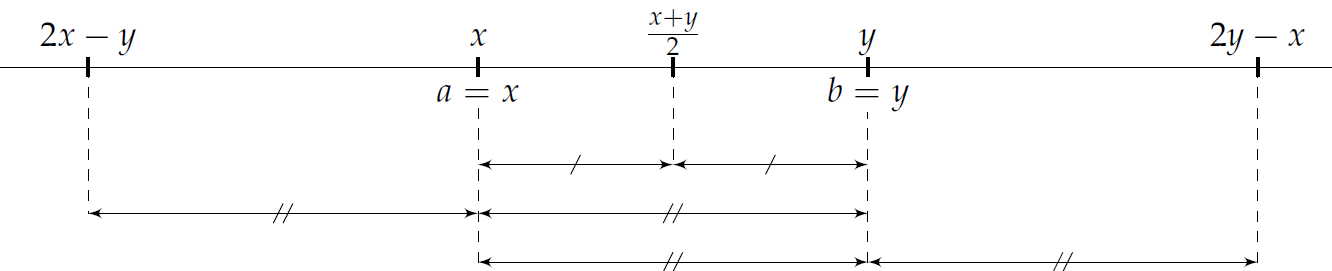
Illustration d'Ivan Boyer. Licence : CC-BY-SA.
Un algorithme pour tester les ensembles bien équilibrés
Vérifier qu'un sous-ensemble $\mathcal{E}$ de $\mathbb{R}$, même fini à $n$ éléments, est bien équilibré peut s'avérer laborieux. Voyons comment systématiser ce travail à l'aide d'un algorithme. On entre d'abord en extension les éléments de $\mathcal{E}$ dans une liste $L$. On en parcourt les paires à l'aide d'un premier indice $i$ balayant $\left[\!\left[0,n-1\right]\!\right]$ et d'un second, $j$, balayant $\left[\!\left[0,i\right]\!\right]$. Puis pour chaque paire $\{i,j\}$ ainsi formée, on se demande si au moins l'un des trois nombres suivants est dans $\mathcal{E}$ :
- $c = \frac{L[i]+L[j]}{2}$, défini comme milieu de $L[i]$ et $L[j]$ ;
- $c = 2L[i]-L[j]$, défini de sorte que $L[i]$ soit au milieu de $L[j]$ et de $c$ ;
- $c = 2L[j]-L[i]$, défini de sorte que $L[j]$ soit au milieu de $L[i]$ et de $c$.
Certaines opérations seront redondantes : quand la paire d'indices $\{i,j\}$ franchit le test pour un certain $c$ convenable dont on remonterait à l'indice $k$, il n'est plus utile d'interroger les paires d'indices $\{i,k\}$ et $\{k,j\}$. De plus, tester une paire $\{i,i\}$ n'a pas grand intérêt, puisque $c = L[i]$ convient immédiatement. Il y aurait donc moyen d'affiner les choses. Plus grave, le programme est sensible aux approximations que commet l'ordinateur. Certaines des valeurs $c$ calculées ci-dessus seront arrondies, ce qui fausse le test d'appartenance à la liste. Voici le code Python correspondant. Il n'est pas optimisé. Il implémente des boucles inconditionnelles assorties d'instructions de sorties, quand des boucles conditionnelles seraient plus esthétiques mais un peu plus difficiles à manier.
def TesterEquilibre(L):
n = len(L)
resultat=True
for i in range(n):
for j in range(i+1):
a,b = L[i],L[j]
c1,c2,c3 = (a+b)/2,2*a-b,2*b-a
if not((c1 in L) or (c2 in L) or (c3 in L)):
resultat = False
break
if resultat == False:
break
return(resultat)
Testons sur l'ensemble $\mathcal{E}=\{0, 1, 2\}$ :
L = [0,1,2]
TesterEquilibre(L)
TRUE
Mis au banc d'essai, le script qualifie correctement les ensembles $\mathcal{E}=\{0,1,2\}$ (qui est bien équilibré), $\mathcal{E}=\{0,2,3,4,6\}$ (qui l'est également), $\mathcal{E}=\{0,1,2,3\}$ (qui ne l'est pas). Il se trompe en revanche sur $\mathcal{E}=\{0,\frac{2}{3},1,\frac{4}{3},2\}$ qu'il croît mal équilibré. La faute au calcul de $2\times 1 - \frac{2}{3}=1,333\ldots$, que la machine arrondit et qu'elle n'identifie donc pas à $\frac{4}{3}$.
Ensembles bien équilibrés finis
Nous décrivons dans cette partie tous les ensembles bien équilibrés finis. Nous en avons déjà reconnus quelques uns : les singletons, mais aussi $\{0,1,2\}$, $\{0, \frac{2}{3}, 1, \frac{4}{3}, 2\}$ et $\{0,2,3,4,6\}$. Notons que les deux derniers sont homothétiques. Plus généralement, la proposition qui suit nous ramène à des sous-ensembles du segment $[0,2]$ par un simple facteur d'échelle doublé d'un changement d'origine.
Proposition
(Homologie)Soit $\mathcal{E}$ un sous-ensemble de $\mathbb{R}$ à $n$ éléments, $n \geq 2$. Posons $m$ le plus petit élément de $\mathcal{E}$, $M$ son plus grand. Les nombres $m$ et $M$ sont distincts puisque $n\geq 2$. Définissons l'application $f$ de $\mathbb{R}$ dans lui-même par $$ f : x \rightarrow 2\frac{x-m}{M-m}. $$ La fonction $f$ applique $\mathcal{E}$ dans $[0,2]$, et les extrémités $0$ et $2$ sont atteintes. De plus, $\mathcal{E}$ est un ensemble bien équilibré si, et seulement si, son image $f(\mathcal{E})$ par $f$ est un ensemble bien équilibré.
Démonstration. L'inclusion $f(\mathcal{E})\subset [0,2]$ découle de ce que pour tout $x$ dans $\mathcal{E}$, $0\leq x-m\leq M-m$. Ajoutons que $f$ atteint, via $m$ et $M$, les bords $0$ et $2$. Enfin, $f$ étant affine et bijective, elle transporte les milieux, et sa réciproque aussi. $\square$
Pour caractériser les ensembles finis bien équilibrés, on peut donc se restreindre à ceux inclus dans $[0,2]$ et dont $0$ et $2$ sont éléments. Énonçons dès lors un nouveau résultat.
Proposition
(Enrichissement)Soit $\mathcal{E}$ un ensemble bien équilibré, inclus dans le segment $[0,2]$ et contenant $0$ et $2$. Dans ce cas,
- $\mathcal{E}$ contient aussi $1$ ;
- si $x$ appartient à $\mathcal{E}$ et $0\lt x\lt 1$, alors $\frac{x+2}{2}$ appartient aussi à $\mathcal{E}$ ;
- si $x$ appartient à $\mathcal{E}$ et $1 \lt x \lt 2$, alors $\frac{x}{2}$ appartient aussi à $\mathcal{E}$.
Démonstration.
- le choix $a=0$ et $b=2$ impose $c=1$, sauf à sortir de l'intervalle $[0,2]$ (avec $-2\lt 0$ ou $4\gt 2$) ;
- le choix $a=x$ et $b=2$ impose $c=\frac{x+2}{2}$ sauf à sortir de l'intervalle $[0,2]$ (avec $2x-2\lt 0$ ou $4-x\gt 2$) ;
- symétriquement, le choix $a=0$ et $b=x$ impose $x = \frac{x}{2}$ sauf à sortir de l'intervalle $[0,2]$ (avec $-x\lt 0$ ou $2x\gt 2$). $\square$
Enchaînons avec le résultat suivant :
Proposition
(Enrichissements successifs)Soit $\mathcal{E}$ un ensemble bien équilibré, inclus dans le segment $[0,2]$ et contenant $0$ et $2$. Si $\mathcal{E}$ contient un élément $x_1$ tel que $0\lt x_1\lt\frac{2}{3}$, alors il contient aussi un élément $x_2$ tel que $0\lt x_1\lt x_2\lt\frac{2}{3}$.
Démonstration. D'après la proposition $2$, deuxième alinéa, $\frac{x_1+2}{2}$ appartient aussi à $\mathcal{E}$. Or, $\frac{x_1+2}{2}>1$. Donc grâce au troisième alinéa, $x_2 = \frac{x_1+2}{4}$ est également dans $\mathcal{E}$. Vérifions les inégalités pressenties :
- $x_1<\frac{2}{3}$ donc $\frac{x_1+2}{4}<\frac{8}{3\times 4} = \frac{2}{3}$ ;
- $x_2-x_1 = \frac{2-3x_1}{4}>0$. $\square$
Par des procédés analogues et sous les mêmes hypothèses, on établirait que :
- si $\mathcal{E}$ contient un élément $x_1$ tel que $\frac{2}{3}\lt x_1\lt 1$, alors il contient aussi un élément $x_2$ tel que $\frac{2}{3}\lt x_2\lt x_1\lt 1$ ;
- si $\mathcal{E}$ contient un élément $x_1$ tel que $1\lt x_1\lt \frac{4}{3}$, alors il contient aussi un élément $x_2$ tel que $1\lt x_1\lt x_2\lt \frac{4}{3}$ ;
- si $\mathcal{E}$ contient un élément $x_1$ tel que $\frac{4}{3}\lt x_1\lt 2$, alors il contient aussi un élément $x_2$ tel que $\frac{4}{3}\lt x_2\lt x_1\lt 2$.
Il est temps de conclure.
Théorème
(Un équilibre rarement atteint...)Il n'existe que trois catégories d'ensembles équilibrés finis : les singletons, et les ensembles se ramenant par homothétie – translation à $\{0,1,2\}$ ou à $\{0, \frac{2}{3}, 1, \frac{4}{3}, 2\}$.
Démonstration. Les candidats déjà passés en revue et la proposition $1$ prouvent que les trois catégories pointées par le théorème conviennent. Démontrons que ce sont les seules. Soit donc $\mathcal{E}$ un ensemble bien équilibré, fini, inclus dans $[0,2]$, contenant les bornes $0$ et $2$. Notons $n$ son nombre d'éléments. Le cas $n=1$ allant de soi, supposons $n\geq 2$.
D'après la proposition $2$, premier alinéa, $1 \in \mathcal{E}$. Donc $n\geq 3$. Si $\mathcal{E}$ contient ne serait-ce qu'un élément $x_1$, strictement intermédiaire à $0$ et $\frac{2}{3}$, le procédé d'enrichissement séquentiel de la proposition $3$ permet d'en échafauder une infinité : $x_2$ avec $0\lt x_1\lt x_2\lt \frac{2}{3}$; $x_3$ avec $0\lt x_1\lt x_2\lt x_3\lt \frac{2}{3}$; etc. Cela est contradictoire avec la finitude de $\mathcal{E}$. À l'avenant, on envisage l'existence d'un élément dans $]\frac{2}{3},1[$, $]1,\frac{4}{3}[$ ou $]\frac{4}{3},2[$. Donc, outre $0$, $1$ et $2$, $\mathcal{E}$ ne peut contenir qu'au plus deux autres éléments : $\frac{2}{3}$ et $\frac{4}{3}$. Or quand il en possède un des deux, mettons $\frac{2}{3}$, il possède l'autre comme conséquence de la proposition $2$. $\square$
Et le cas infini ?
Ouvrons une fenêtre sur les ensembles bien équilibrés infinis. Bien sûr il en existe, à commencer par $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, les intervalles de $\mathbb{R}$ voire $\mathbb{R}$ lui-même ! Donnons deux autres exemples.
- l'ensemble des nombres dyadiques, c'est-à-dire du genre $\frac{u}{2^v}$ avec $u \in \mathbb{Z}$ et $v \in \mathbb{N}$, est bien équilibré car stable par passage au milieu ;
- l'ensemble des nombres irrationnels, $\mathbb{R}\backslash\mathbb{Q}$ est aussi bien équilibré. En effet, pour $a \in \mathbb{R}\backslash\mathbb{Q}$ et $b \in \mathbb{R}\backslash\mathbb{Q}$, l'un des deux nombres $c=\frac{a+b}{2}$ ou $c'=2a-b$ est irrationnel. Dans le cas contraire, on exprimerait $a$ par exemple en fonction de $c$ et $c'$, soit $$ a = \frac{2c+c'}{3} $$ dont on déduirait la rationalité. C'est absurde.