Je dessine depuis longtemps, en marge de mes cahiers et de mon métier de professeur de mathématiques. Depuis dix ans, dès que l’idée se présente, j’aime faire des planches en rapport avec les mathématiques. Elles sont souvent autonomes, n’ayant pas de rapport les unes avec les autres, il n’y a pas de personnages récurrents car le principal enjeu de la planche est de présenter ou d’utiliser une propriété géométrique ou algébrique de façon ludique. De nombreuses planches ont été dessinées pour le concours Bulles au carré organisé par le site « images des maths ».

La bande dessinée peut parfois jouer avec ses composantes, et à l’instar de l’OuLiPo (ouvroir de littérature potentielle, créée en 1960 par le mathématicien François LeLionnais et Raymond Queneau) qui allie littérature et mathématiques pour fabriquer des objets littéraires à la forme inédite, on peut aussi jouer avec les éléments qui constituent la bande dessinée. L’OuBaPo, une petite sœur de l’OuLiPo expérimente depuis plus de vingt ans des bandes dessinées à contraintes, et certaines planches, notamment celles d’Etienne Lécroart, utilisent les mathématiques comme inspiratrice de la forme. J’ai été grandement influencé par ces planches et j’ai naturellement cherché dans cette voie.

La contrainte peut porter sur de nombreuses composantes de la bande dessinée (texte, dessin, couleur, personnage, histoire, mise en page). Pour ma part, j’explore surtout les possibilités de la mise en page.

La plupart du temps, mon objectif principal est d’illustrer une formule mathématique, d’en faire un petit objet amusant à lire puis à comprendre. Cela se prête particulièrement aux suites et aux séries géométriques.

Un terme d’une suite peut être figuré par une longueur de case. Si toutes ces cases ont une largeur constante, alors les aires des rectangles obtenus sont proportionnelles à ces longueurs. Cette astuce permet de faire la mise en page de mes planches. Ensuite, il faut trouver une histoire qui colle bien à la formule illustrée, suivant le principe oulipien de Roubaud (un texte écrit sous contrainte parle de cette contrainte). Dans le cas de la planche sur la série harmonique, publiée ici, l’approche historique et l’explication de la démonstration semblait naturelle.

Un exemple

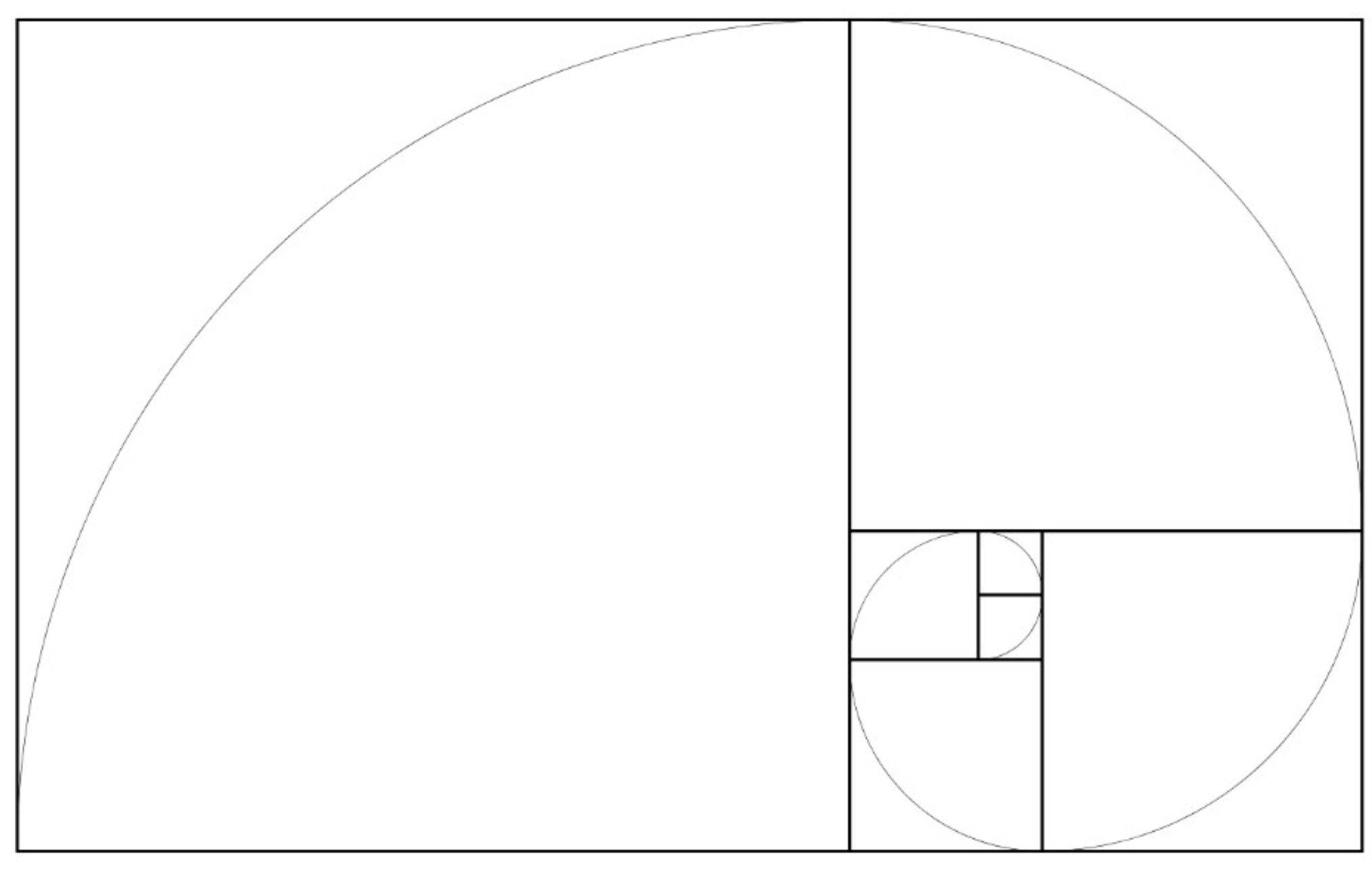
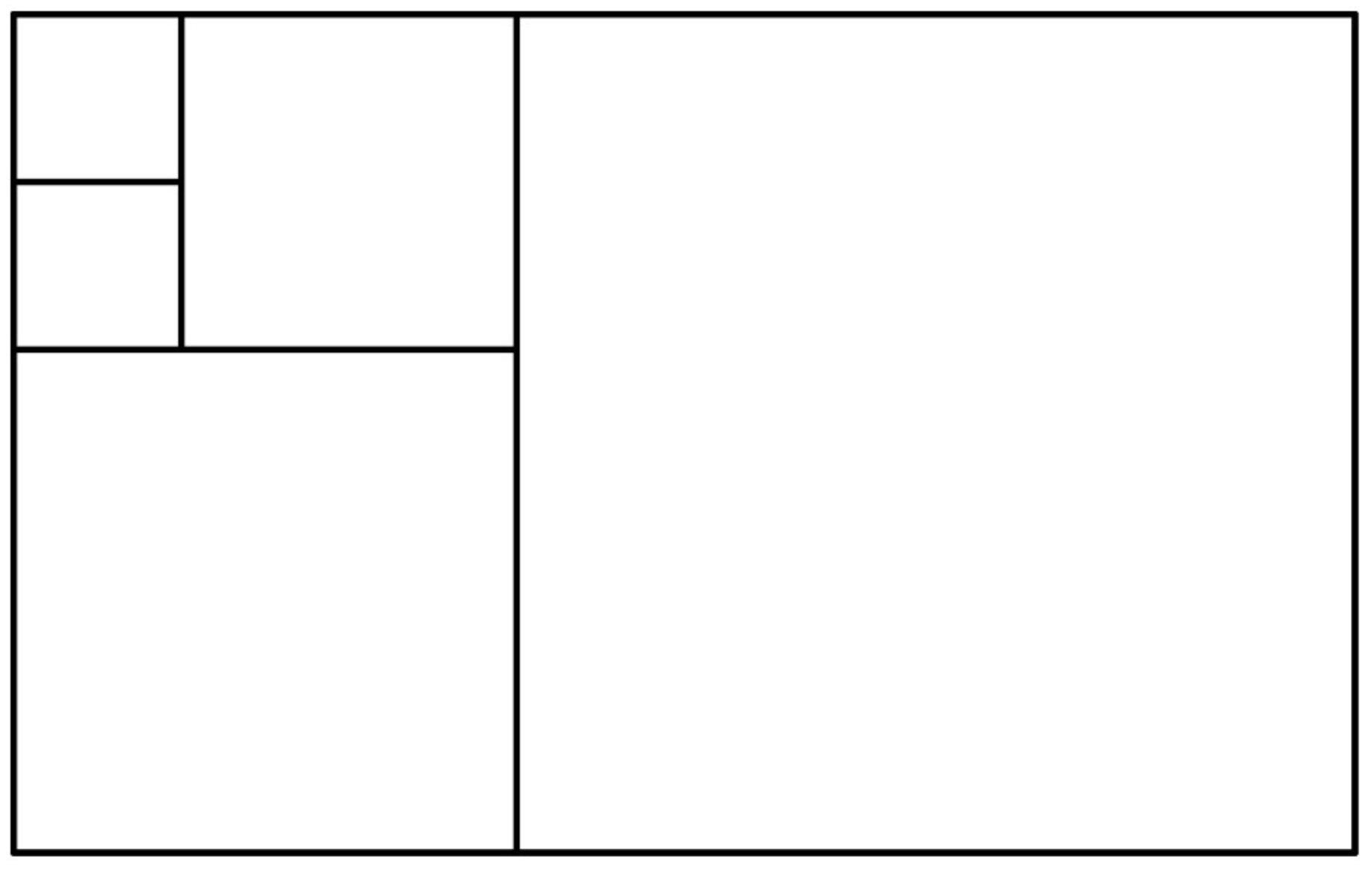
Vous connaissez certainement des figures illustrant des suites, par exemple, la suite de Fibonacci :

$$ \left\{\begin{aligned} F_0 &=F_1=1 \\ F_{n+2} & =F_n+F_{n+1} \end{aligned}\right. $$

Par construction, les carrés ont pour longueur de côté les termes de la suite. Ici, l’aire de chaque carré est proportionnelle au carré de chaque terme. On voit souvent cette image pour expliquer la construction d’un tableau, mais ne voit-on pas dans la deuxième disposition les cases d’une planche de bande dessinée ?

Dans ces exemples se pose la question de la gouttière, la bande blanche qui sépare deux cases. On peut y voir le temps qui s’est passé entre ces deux cases. La gouttière peut-elle rentrer dans les calculs ?

Parfois on peut mettre des gouttières de largeur différente en fonction des longueurs des cases qui l’entourent, mais c’est souvent difficile de la placer sans changer les proportions des cases entre elles. Dans ces deux cas, je ne peux pas mettre de gouttière, les rectangles sont seulement juxtaposés.

L’un des plaisirs pour le lecteur est, après lecture de la planche, de regarder la méthode de sa construction. Certains auteurs de BD pensent que pour réussir un effet de narration par une mise en page astucieuse, il ne faut pas voir comment il a été produit, surtout si c’est une histoire qui tient sur de nombreuses planches. Sentir l’effet, ne pas le comprendre, et poursuivre la lecture. Pour une planche unique, je ne pense pas qu’il faut être aussi subtil. Je ne suis pas un magicien, je veux qu’on trouve mon truc, qu’on trouve l’analogie entre la forme des cases et les nombres mis en jeu. Si ça peut lancer des lecteurs dans des vérifications et des calculs, je serai content, car l’émerveillement à mon avis est dans la formule, sa compréhension et mes planches ne sont qu’une invitation à les découvrir.