Iconographie commentée et petits problèmes issues de L'algèbre arabe - Genèse d'un art, annexe 2
Sommaire (cliquer sur l'image)
 1-Diophante |
2-Brahmagupta |
3-Al-Khwârizmî |
4-Al-Khwârizmî |
|---|---|---|---|
5-Al-Khwârizmî |
6-Al-Khwârizmî |
7-Ibn Turk |
8-Al-Karajî |
9-Al-Khwârizmî en latin |
10-As-Samaw’al |
11-Ibn al-Yâsamîn |
12-Ibn Qunfudh |
13-Ibn Haydûr |
14-Al-Qatrawânî |
15-Ibn Ghâzî |
16-anonyme |
17-Cordoue |
18-Cordoue |
19-Grenade |
20-Marrakech |
Les Arithmétiques, traduction arabe par Qustâ Ibn Lûqâ (m. 910)
Une page de la traduction partielle des Arithmétiques.
Problème - Trouver deux cubes dont la somme est un nombre carré.
Manuscrit en papier qui date probablement du XIXe siècle. Copie d'un traité de Brahmagupta (629 après Jésus-Christ).
Couverture d’une copie du livre d’algèbre d’al-Khwârizmî, réalisée au XIIIe siècle.
Problème - Dix que tu divises en deux parties, tu multiplies l'une des deux parties par elle-même et elle devient comme l'autre quatre-vingt et une fois.
al-Kitâb al-mukhtasar fî hisâb al-jabr wa l-muqâbala [Livre abrégé sur le calcul par la restauration et la comparaison]
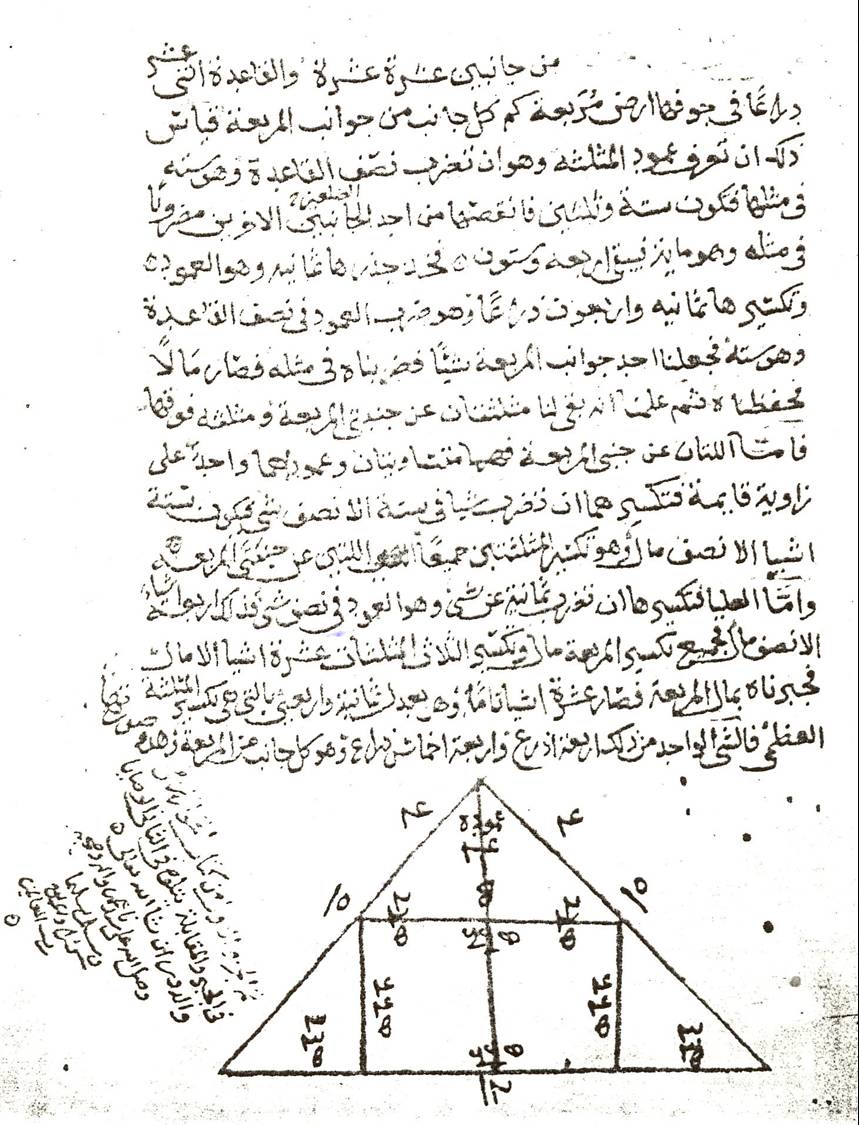
Problème d’inscription d’un carré dans un triangle isocèle résolu par l’algèbre puisqu’il aboutit à une équation du premier degré.
Problème - Si on dit : une terre triangulaire, ses deux côtés ont dix coudées, dix coudées, et la base douze coudées, et dans son ventre une terre carrée. Quel est le côté du carré ?
5- Statue moderne d'al-Khwârizmî à Khiva, Ouzbékistan
[Photo Alain Juhel]
Problème - Un homme meurt et laisse quatre fils et il fait, à un homme, une donation égale à la part de l'un de ses fils et à un autre le quart de ce qui reste du tiers. Quelle est la part de l'un de ses fils ?
6- Portrait moderne d'al-Khwârizmî
Timbre soviétique à l’effigie supposée d’al-Khwârizmî.
Problème - Si on dit : une fortune, tu en sépares son tiers et trois dirhams et tu multiplies ce qui reste par lui-même, alors revient la fortune. Quelle est la fortune ?
Kitâb al-jabr [Livre d’algèbre]
Page d’un livre d’algèbre publié à la même époque que le fameux livre d’al-Khwarizmî et qui a suscité une polémique sur la priorité de ce dernier ou d’Ibn Turk dans la publication du premier ouvrage d’algèbre.
Al-Kitâb al-Fakhrî [Le livre fakhrien]
Il s’agit des démonstrations géométriques de l’existence des solutions positives d’une équation du second degré.
Problème- Si on te dit : un bassin dans lequel coulent trois rivières. L'une d'elles le remplit en un jour, la seconde en deux jours et la troisième en trois jours. On ouvre toutes les rivières. En combien d'heures le remplissent-elles ?
Al-Khwârizmî : Livre d’algèbre. Traduction latine de Robert de Chester.
Le livre d’al-Khwârizmî a bénéficié de trois traductions en latin : celle de Gérard de Crémone (1114-1187), celle de Robert de Chester (ca 1141) et celle de Guillaume de Lunis (XIIIe s.).
10- Le triangle arithmétique attribué à Al-Karajî
As-Samaw’al (m. 1175) : al-Kitâb al-bâhir fî l-jabr [Le livre flamboyant en algèbre]
As-Samaw’al attribue ce triangle à al-Karajî qui l’aurait publié dans un livre qui nous est parvenu. Il a été construit pour obtenir les coefficients du binôme.
11- Poème mathématique d'Ibn al-Yâsamîn
Ibn al-Yâsamîn (m. 1202) : al-Yâsamîniyya fî l-jabr [Le poème Yâsamîniyya en algèbre]
C’est un poème de plus de cinquante vers qui contient les éléments de base de l’algèbre : l’inconnue, son carré, les équations et leurs algorithmes de résolution.
Ibn Qunfudh (m. 1407) : Hatt an-niqâb ôan wujûh a ômâl al-hisâb [L’abaissement de la voilette sur les formes des opérations du calcul]
Le dessin représente les deux plateaux d’une balance. C’est la raison pour laquelle la méthode « de fausse position » est appelée, au Maghreb, la méthode « des plateaux ». Dans les ouvrages mathématiques arabe d’Orient, elle est appelée la méthode « des deux erreurs ».
Ibn Haydûr (m. 1413) : Kitâb at-Tamhîs fî sharh at-Talkhîs [Livre d’analyse sur le commentaire de l’Abrégé]
Il s’agit de la même méthode de double fausse position mais appliquée cette fois à la résolution d’un système d’équations.
14- Écriture symbolique d'un polynôme
Al-Qatrawânî (XVe) : Rashfat ar-rudâb min thughûr a ômâl al-hisâb [La succion du nectar des bouches des opérations du calcul]
La page contient une écriture en symboles d’un polynôme de degré 6. Dans ce livre l’auteur effectue des opérations arithmétiques sur les polynômes, en particulier l’extraction de la racine cubique d’un polynôme.
15- Écriture symbolique d'une équation
Ibn Ghâzî (m. 1513) : Bughyat at-tullâb fî sharh Munyat al-hussâb [Le désir des étudiants sur le commentaire du souhait des calculateurs]
La page illustre la résolution complète d’un problème d’arithmétique après sa mise en équation, en utilisant éclusivement l’écriture symbolique du Maghreb. Il s’agit du problème suivant : déterminer $n$ tel que : $1\times 3 + 3\times 3 + 5\times 3 +\cdots + (2n+1)\times 3 = 1225$.
16- Écriture symbolique d'une équation (anonyme)
Manuscrit anonyme contenant une équation écrite à l’aide des symboles algébriques utilisés au Maghreb entre le XIIe et le XIXe siècle.
17- Mosquée-cathédrale de Cordoue
18 - Mosquée-cathédrale de Cordoue
20- Madrassa Ibn Yusuf de Marrakech
