Introduction

Pour cette nuit de l'ENS dont le thème est l'« incertitude », je me propose de démontrer rigoureusement un théorème mathématique, dont l'énoncé est le suivant.

Mais qu'est-ce que ce théorème signifie ? Ni « connaissance » ni « incertitude » ne sont des mots appartenant au vocabulaire classique des mathématiques. Il faut donc d'abord comprendre le sens de ces mots :

• qu'est-ce que l'incertitude ?
• qu'est-ce que la connaissance ?

Vaste programme !

En mathématiques, relier par des définitions des mots à des objets ou concepts mathématiques est une chose courante. Henri Poincaré, dans sa Science et méthode (1908), affirme que

Il insiste ainsi à la fois sur l'importance du choix du mot et sur le processus d'abstraction inhérent au mathématiques. Mais le mathématicien reste entièrement libre du choix de ses mots ! David Hilbert, chantre de la méthode axiomatique, va plus loin : en 1891, au retour d'une conférence sur la géométrie, il déclara :

Pourquoi, en effet, maintenir une référence à des objets géométriques intuitifs si la science mathématique est par essence une science abstraite ? Ainsi, on peut fort bien énoncer :

Cela est « parfaitement » (c'est-à-dire mathématiquement) correct ! Dans la même veine, pour démontrer notre théorème « la connaissance réduit l'incertitude. » on pourrait très bien poursuivre la boutade de Hilbert et nommer, par exemple, les choses ainsi :

La preuve de notre théorème est alors immédiate :

Démonstration. $42$ divisé par $2$ égale $21$ ; mais $21$ est inférieur à $42$. Donc, la connaissance réduit l'incertitude. CQFD ! $\square$

Tout cela est évidemment du grand n'importe quoi , les définitions choisies sont absurdes, et la science mathématique ne doit pas simplement jouer sur des éléments logiques arbitraires : les mathématiques restent malgré tout faites par des humains, qui vivent dans le monde réel (même s'il est parfois complexe...). Elles ne trouvent leur intérêt qu'avec des liens, même vagues ou intuitifs, à des concepts qui nous parlent.

Il faut donc revenir à une définition sensée de l'incertitude et de la connaissance. Quelle définition adopter qui ait vraiment un sens, en plus d'une simple traduction mathématique ?

Qu'est-ce que l'incertitude ?

Il y a évidemment de multiples approches possibles. Je retiens la définition suivante, trouvée au hasard dans un dictionnaire :

incertain : Qui n'est pas sûr, qui peut se produire ou non.

Cela me semble être une description probabiliste d'un phénomène d'incertitude. C'est heureux, car on pourra l'interpréter mathématiquement si on fait appel à la théorie mathématique des probabilités. Supposons que l'on observe, par exemple, un événement de probabilité $p$, compris entre 0% et 100% (de chances de se produire). Peut-on alors définir l'incertitude $i$ comme une fonction de $p$ ?

Il est intéressant de noter ici qu'on cherche à définir une mesure d'incertitude plutôt que l'incertitude elle-même ; mais c'est bien ce qui est requis dans le cadre de notre théorème. Cette (mesure d') incertitude $i(p)$ sera donc un nombre réel positif.

Comment, alors, définir $i(p)$ ? Comment évaluer ou calculer l'incertitude ? Il y a clairement des propriétés naturelles, suggérées par notre intuition. On peut, par exemple, en retenir deux :

1. un événement doit être d'autant plus incertain qu'il a moins de chances de se produire ;
2. si deux événements n'ont rien à voir entre eux, leurs incertitudes respectives ne font que se cumuler l'un l'autre en s'ajoutant.

Traduits mathématiquement, ces deux postulats deviennent des axiomes mathématiques :

1. $i(p)$ est d'autant plus grand que $p$ est petit : la fonction $i$ est une fonction décroissante de $p$ ;
2. si deux événements de probabilités respectives $p$ et $q$ sont indépendants, leur probabilité conjointe est le produit $pq$, de sorte que $i(pq)=i(p)+i(q)$ : la fonction $i$ transforme produit en somme.

On adopte donc ici une méthode axiomatique qui consiste à déduire de ces axiomes l'expression mathématique de l'incertitude $i(p)$ en fonction de $p$. Le résultat est un théorème :

Démonstration. Commençons par appliquer le deuxième axiome un grand nombre de fois sur un produit de $n$ probabilités égales : $p^n=p\times p \times \cdots \times p$ ($n$ fois) aura pour incertitude $i(p^n)=i(p)+i(p)+\cdots+i(p)$ ($n$ fois), c'est-à-dire $$ i(p^n)=n\cdot i(p). $$ Si la probabilité initiale n'est pas de 100%, c'est-à-dire $p\lt 1$, la probabilité composée $p^n$ est rapidement très petite lorsque $n$ devient grand, de la forme $p=0,000000\ldots000000c$ avec $r$ zéros après la virgule avant le premier chiffre non nul $c$. Autrement dit, posons $r$ le rang du premier chiffre significatif $c$ dans $p^n$. On a alors les inégalités1 : $$ \Bigl(\frac{1}{10}\Bigr)^r \geqslant p^n \geqslant \Bigl(\frac{1}{10}\Bigr)^{r+1}. $$ Appliquons maintenant le premier axiome : en appliquant la fonction $i$ recherchée, les inégalités s'inversent : $$ i \Bigl(\Bigl(\frac{1}{10}\Bigr)^r\Bigr) \leqslant i(p^n) \leqslant i\Bigl(\Bigl(\frac{1}{10}\Bigr)^{r+1}\Bigr) $$ ce qui revient, par la formule précédemment établie, à $$ r\cdot i \Bigl(\frac{1}{10}\Bigr) \leqslant n\cdot i(p) \leqslant (r+1)\cdot i\Bigl(\frac{1}{10}\Bigr) $$ ou encore, en divisant par $n$ après avoir posé la constante positive $C=i \bigl(\frac{1}{10}\bigr)$ : $$ \frac{r}{n}\cdot C \leqslant i(p) \leqslant \bigl(\frac{r}{n}+\frac{1}{n}\bigr)\cdot C. $$ Ce qu'on obtient finalement, c'est qu'à une constante multiplicative près, $i(p)$ tombe dans un tout petit intervalle $[\frac{r}{n}; \frac{r}{n}+\frac{1}{n}]$ de longueur $\frac{1}{n}$. Cette longueur peu être rendue aussi petite que l'on veut en prenant $n$ suffisamment grand, ce qui permet de déterminer « asymptotiquement » l'incertitude $i(p)$ avec une précision aussi grande qu'on veut.

Pour conclure enfin, il suffit de remarquer que la fonction $\log \frac{1}{p}$ vérifie déjà les deux axiomes : c'est bien une fonction décroissante de $p$, et le logarithme transforme bien produit en somme. Par conséquent, on peut lui appliquer le même traitement qu'à la fonction $i(p)$ ! On obtient alors, qu'à une constante multiplicative près2, $\log \frac{1}{p}$ tombe également dans le même intervalle $[\frac{r}{n}; \frac{r}{n}+\frac{1}{n}]$ de longueur arbitrairement petite. Les deux quantités $i(p)$ et $\log\frac{1}{p}$ ne sont donc distantes que d'au plus $\frac{1}{n}$ et ceci pour tout $n$ même très grand ! Cela n'est possible que si ces deux quantités sont en fait égales, toujours à une constante multiplicative $c$ près3 : $$ i(p) = c \cdot \log\frac{1}{p}. $$ Mais en réalité, le logarithme dans cette formule n'est lui-même défini qu'à une constante multiplicative près. Cela dépend, en effet, de la base du logarithme que l'on choisit4. Par conséquent, faire intervenir la constante $c$ dans cette formule est inutile, et obtient bien l'identité qu'il fallait démontrer.$\square$

Incertitude moyenne et entropie de Shannon

En résumé, on a jusqu'à présent déterminé l'incertitude comme une mesure logarithmique pour un événement donné. Mais l'intérêt d'un tel résultat pour l'instant limité car on ne tient compte que d'un seul événement. Il est plus intéressant, en théorie des probabilités, de manipuler des lois de probabilité, c'est-à-dire tout en ensemble de probabilités que l'on décrit à l'aide de la notion de variable aléatoire.

Sans entrer dans les détails7, une variable aléatoire $X$ est une quantité qui peut prendre plusieurs « valeurs »8. Si $X$ prend la valeur $x$, c'est avec la probabilité $p(x)$ de l'événement $X=x$. Chaque événement $X=x$ de probabilité $p(x)$ a donc, d'après ce qu'on a déjà établi, une incertitude $$ i(x) = \log \frac{1}{p(x)}. $$ L'incertitude moyenne — en moyenne sur toutes les valeurs possibles de $X$ — s'obtient en sommant ces incertitudes $i(x)$ pondérées par les probabilités d'occurence $p(x)$ : on obtient ainsi9 $$ H(X) = \sum_x p(x) \log \frac{1}{p(x)} $$ connu sous le nom d'entropie de Shannon.

On peut vérifier que cette notion d'incertitude moyenne correspond bien à nos attentes. Tout d'abord, c'est une quantité positive (car somme de termes tous positifs) qui ne s'annule que lorsque chacun des termes s'annule. Cette dernière condition équivaut11 à $p(x)=0$ ou $1$ pour tout $x$. Cela revient encore à dire qu'une seule valeur de $X$ est probable, les autres étant de probabilité nulle : $X$ est totalement certaine, elle n'est plus aléatoire ! Ainsi une incertitude nulle correspond bien au cas certain : $$ H(X)=0 \iff X \text{ est certaine}. $$ À l'opposé, supposons l'incertitude moyenne maximale pour une variable aléatoire $X$ pouvant prendre un nombre fini $M$ de valeurs possibles. On montre facilement que $H(X)$ est une fonction symétrique et concave12 des probabilités $p(x)$ et que par conséquent, sa valeur maximum ne peut être atteinte que lorsque tout les probabilités $p(x)$ sont égales. Cela revient à dire que $p(x)=\frac{1}{M}$ pour tout $x$, ce qui donne une incertitude moyenne maximale $H(X)=\log M$, le logarithme du nombre de possibilités. En d'autres termes, le cas le plus incertain correspond à une variable aléatoire uniforme, dont aucune valeur n'est plus probable qu'une autre : $$ H(X) \text{ maximale} =\log M \iff X \text{ est uniforme}. $$ Cela correspond bien à l'idée que l'on se fait d'alternatives équiprobables dans le cas le plus incertain.

Qu'est-ce que la connaissance ?

Là encore, vaste programme ! Mais restreignons nous à notre cadre mathématique probabiliste où nous avons défini l'incertitude $H(X)$. En théorie des probabilités, il y a une façon naturelle de prendre en compte une donnée connue, ou la connaissance d'un événement. On définit en effet la probabilité conditionnelle d'un événement connaissant (ou sachant) un autre événement.

Pour notre variable aléatoire $X$, supposons qu'on connaisse la réalisation d'une autre variable aléatoire $Y$, disons l'événement $Y=y$. La connaissance de cet événement va modifier la loi de probabilité $p(x)$ de la variable initiale $X$. En effet, la nouvelle loi devient la loi conditionnelle définie par la formule célèbre13 $$ p(x|y) = \frac{p(x,y)}{p(y)} $$ où $p(x,y)$ désigne la probabilité conjointe des événements $X=x$ et $Y=y$ et $p(y)$ la probabilité de l'événement connu $Y=y$.

La nouvelle entropie (incertitude moyenne) connaissant $Y=y$ devient $$ H(X|Y=y) = \sum_x p(x|y) \log \frac{1}{p(x|y)} $$ qui dépend de la valeur $y$.

Si nous voulons maintenant évaluer l'incertitude moyenne sur $X$ connaissant $Y$ en général (pour n'importe quelle valeur possible $y$), il faut encore moyenner ces valeurs de $Y$ — c'est-à-dire sommer les entropies $H(X|Y=y)$ pondérées par les probabilités d'occurrence respectives $p(y)$ : on obtient alors l'entropie conditionnelle : $$ \begin{aligned} H(X|Y) & = \sum_y p(y) H(X|Y=y) \\ & =\sum_{x,y} p(x|y)p(y) \log \frac{1}{p(x|y)} \\ & =\sum_{x,y} p(x,y) \log \frac{1}{p(x|y)} \end{aligned} $$

On vérifie, là encore, que cette quantité correspond bien à notre intuition. Supposons, par exemple, que les variables $X$ et $Y$ n'ont « rien à voir » entre elles, c'est-à-dire qu'elles sont indépendantes. Dans ce cas, la probabilité conjointe des deux événements indépendants $X=x$ et $Y=y$ et le produit des probabilités individuelles : $p(x,y)=p(x)p(y)$. La définition de la probabilité conditionelle donne alors $p(x|y)=p(x)$, qui ne dépend effectivement pas de $y$, de sorte que $H(X|Y=y)=H(X)$ pour tout $y$, et donc en moyenne $H(X|Y)=H(X)$ : ici, la connaissance de $Y$ na pas changé l'incertitude sur $X$ — c'est normal puisque $Y$ est indépendante de $X$ !

Revenons alors à notre théorème initial : « la connaissance réduit l'incertitude ». Ce qu'il exprime maintenant, c'est que, lorsque $Y$ dépend de $X$, sa connaissance va diminuer l'incertitude sur $X$ :

Démonstration du théorème

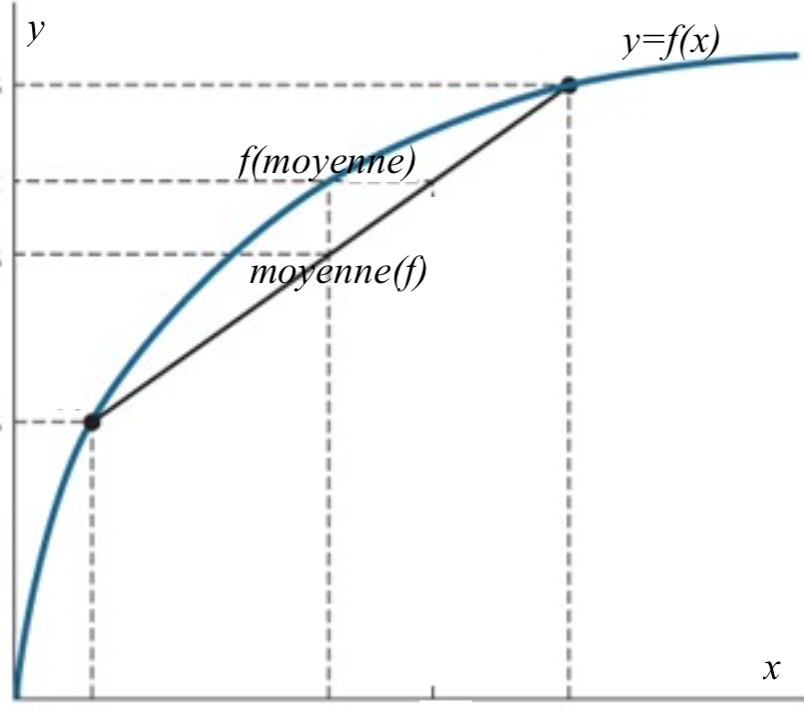
La formule des probabilités totales nous dit que $$ p(x)=\sum_y p(x,y) = \sum_y p(y) p(x|y). $$ Autrement la probabilité (inconditionnelle) $p(x)$ s'obtient en moyennant (sur $y$) les probabilités conditionnelles $p(x|y)$. Ce type de moyenne se retrouve aussi dans l'expression de l'entropie conditionnelle : $$ H(X|Y) = \sum_y p(y) H(X|Y=y) $$ et on peut comparer les deux formules par une inégalité de concavité. On a vu, en effet, que l'entropie est une fonction concave de la loi de probabilité. En particulier, $H(X|Y=y)$ est une fonction concave de $p(x|y)$.

L'inégalité de concavité (du mathématicien danois Johan Jensen, 1906) s'obtient en disant que qu'une moyenne des valeurs d'une fonction concave est toujours inférieure (ou égale) à la fonction concave évaluée en la moyenne de ces valeurs (voir la figure 1). Ici la moyenne de $H(X|Y=y)$ (suivant les valeurs de $y$) est l'entropie conditionnelle $H(X|Y)$. Elle est donc inférieure ou égale à l'entropie de la moyenne des $p(x|y)$, c'est-à-dire de la loi inconditionnelle $p(x)$. Cette dernière entropie n'est autre que $H(X)$. On a donc bien prouvé que $H(X|Y)\leqslant H(X)$. CQFD !$\square$

Vraiment ? L'exemple du canal en $Z$

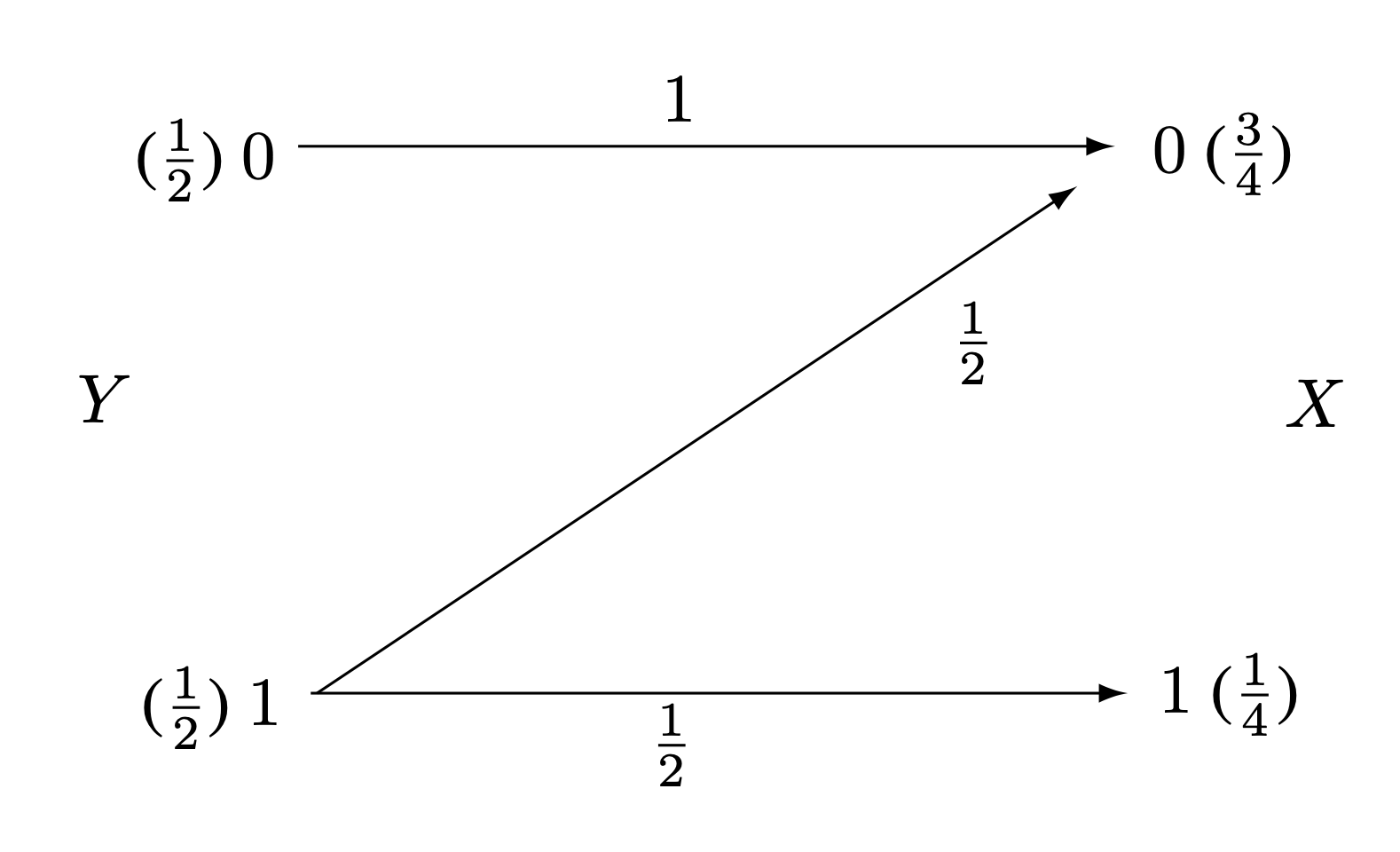
Prenons l'exemple du « canal » binaire de la figure ci-dessus où $X$ s'obtient à partir de $Y$ selon deux modalités :

• ou bien $Y=0$, auquel cas on a nécessairement $X=0$ ;
• ou bien $Y=1$, auquel cas on a indifféremment $X=0$ ou $1$ avec probabilités égales.

Un petit calcul montre que $H(X)=\frac{1}{4}\log 4 + \frac{3}{4}\log \frac{4}{3}=0.811278124\ldots$ bits, alors que $$H(X|Y=0)=0 \text{ bit}$$ (car sachant que $Y=0$ on sait d'avance que $X=0$), en revanche $$ H(X|Y=1)=1 \text{ bit}$$ (car sachant que $Y=1$, on a un choix équiprobable d'un bit sur deux).

On voit ici que la connaissance de $Y=1$ accroît l'incertitude sur $X$ au lieu de la réduire, puisque $H(X|Y=1)\gt H(X)$ ! Mais cet accroissement est « local », car en revanche la connaissance de $Y=0$ réduit bien l'incertitude sur $X$ et en moyenne, on a bien $H(X|Y)=0.5$ bit $\lt H(X)$.

Cet exemple montre que, comme souvent dans la vie quotidienne, la connaissance d'un événement donné peut parfois, paradoxalement, augmenter l'incertitude au lieu de la réduire. Et c'est quelque chose que nous devons, à mon avis, méditer !