Pour l’édition 2022 de la Nuit des sciences et des lettres de l’ENS, lors de la conférence conjointe avec Olivier Rioul, intitulée « Incertitude et connaissance : la polysémie mathématique et linguistique », je suis partie de l’hypothèse que l’acquisition et la transmission des connaissances passent nécessairement par une version plus ou moins hybride du langage naturel, et que les mathématiques n’en sont pas exemptes (pensez aux expressions comme « donc », « si et seulement si », « soit x tel que », « supposons que », etc.). Cependant, avec le langage ordinaire vient très souvent la polysémie, car un mot (ou une phrase) peut avoir plusieurs sens, plusieurs interprétations possibles. Est-il possible de trouver des vertus à cette incertitude polysémique même dans un langage hautement formalisé, comme celui des mathématiques ?
 

Olivier Rioul a montré qu’il est possible de mathématiser les notions de connaissance et d'incertitude et de démontrer formellement que l’énoncé « la connaissance réduit l’incertitude » est vrai. De manière complémentaire (si l’on considère les mathématiques comme un langage formel), on peut s’intéresser à la signification de cet énoncé du point de vue linguistique, c'est-à-dire du langage naturel.
Avant de mathématiser la proposition « la connaissance réduit l’incertitude », et avant même de réfléchir sur la vérité de cette proposition, il faut passer par une étape préliminaire d’abstraction, qui semble si évidente qu’on n’y pense même pas : il faut comprendre ce que cela veut dire. Cependant, ce que l’on considère comme une évidence comporte souvent un piège, un biais, qui consiste à prendre quelque chose qui relève de notre point de vue, qui est donc particulier, pour une valeur universelle de la chose ou du phénomène observé (celui dont on perçoit l’évidence). Autrement dit, pour comprendre la proposition « la connaissance réduit l’incertitude », on doit commencer par dire ce que l’on entend par « connaissance », et par « incertitude », et par « réduire ».

Imaginez que vous devez écrire une dissertation, et que l’on vous propose comme sujet le même énoncé, sous forme de question : « Est-ce que la connaissance réduit l’incertitude ? ». Vous seriez alors obligés, sinon de faire un plan en trois parties, au moins de donner un pour et un contre, tous les deux argumentés, en jouant avec la multiplicité des sens possibles des notions de connaissance et d’incertitude.

On pourrait imaginer un plan comme le suivant :

• la connaissance réduit l’incertitude lorsque l’on comprend l’incertitude comme une sorte d’ignorance, et puisque la connaissance et l’ignorance sont des termes contradictoires, alors augmenter la quantité de l'un diminue la quantité de l’autre ;
• la connaissance augmente l’incertitude car chaque connaissance véritablement nouvelle ouvre la possibilité de découvrir des pans entiers de choses inconnues, inexplorées, et incertaines ;
• et l’incertitude et la connaissance ont la même cardinalité, pour emprunter un mot mathématique (dans le sens où à chaque incertitude correspond une connaissance qui la résout) et aucune n’augmente ni ne décroît en fonction de l’autre.

Dans la première réponse on a précisé ce qu’on entendait par incertitude en donnant un synonyme ; dans la deuxième on a modulé la notion de la connaissance, impliquant qu’il en existe plusieurs types, en qualifiant celle dont on voulait parler par « véritablement nouvelle ». Dans la troisième, c’est la notion même de réduction qui a été marquée comme non-pertinente dans un contexte des grandeurs infinies. Notons qu'en utilisant le terme « cardinalité », on utilise effectivement un mot mathématique dans un sens métaphorique, ce qui indique que le fait de connaître certains objets mathématiques influence la façon dont on voit le monde réel.

Pour sortir de l’incertitude sur la bonne interprétation parmi plusieurs possibilités de comprendre une même phrase, on a besoin de connaître le « vouloir dire » du locuteur (ou de l'auteur !). Le fait qu’il est possible de l’articuler de plusieurs façons différentes est dû, au moins en partie, à la polysémie.

Qu'est-ce que la polysémie ?

Voici une définition classique, sémantico-lexicale de la polysémie : c'est la propriété qui relie un mot à plusieurs sens apparentés, qui créent un champ sémantique de ce mot.
Le fait que les sens soient apparentés distingue la polysémie de l’homonymie. Cette distinction est également marquée dans les dictionnaires : chaque homonyme est considéré comme un mot à part, et il aura une entrée individuelle dans le dictionnaire, alors que les différents sens d'un mot polysémique seront listés dans le cadre de ce mot. Par exemple :

• un mineur (travailleur dans les mines), et
• un mineur (enfant qui n’a pas atteint l’âge légal de la majorité)

sont des homonymes.

Par contre, l’adjectif mineur utilisé pour désigner

• un mode mineur (en musique) et
• un terme mineur (en logique)

est polysémique.

Ces définitions constituent une sorte de code. De ce point de vue, les langues naturelles sont des systèmes codiques, des systèmes d’appariement sons-sens ; c’est la première couche, linguistique, de la communication ; elle est nécessaire, mais incomplète. Pour comprendre entièrement le message que nous communique quelqu’un qui dirait, par exemple, que « la connaissance réduit l’incertitude », il faut aller au-delà de ce plan de significations lexicales des mots, autrement dit, au-delà de l’information que l’on trouve dans un dictionnaire. Il faut passer du code à l’inférence. Le lecteur ou l’auditeur doit inférer le « vouloir dire » du locuteur, son intention informative1: ce n’est pas un simple décodage, mais un raisonnement qui permet d’aller au-delà de ce qui est écrit, de comprendre éventuellement le sens non-littéral d’un énoncé. C’est par cette brèche que peut se faufiler une variante de l’incertitude : le message n’est pas seulement encodé (donc monosémique, une fois qu’une polysémie potentielle se trouve résolue dans le contexte), mais il comporte également des ouvertures vers des intentions de son créateur (il était peut-être ironique ? ou facétieux ? ou elliptique ?), la question qui se pose est : comment être sûr d’avoir compris ce qu’il voulait dire ?

Quand est-ce que la polysémie pose un problème ?

Le traitement automatique des langues

Le domaine dans lequel l’incertitude due à la polysémie est réellement un problème difficile à résoudre est le traitement automatique des langues, précisément à cause de cette incapacité de la machine d’aller au-delà de ce qui est écrit, c’est à dire d’inférer le sens avec certitude. La machine décodera avec précision le sémantisme ponctuel des mots lorsqu’il se trouvent en intersection avec une syntaxe, i.e. les règles grammaticales bien définies, mais puisqu’elle possède uniquement le modèle du code, et non pas le modèle de l’inférence (au sens pragmatique de ses termes évoqué ci-dessus), elle ne saura pas quoi faire, ou pire, fera des erreurs d’interprétation dans tous les cas où il existe cette pluralité des sens, où les unités linguistiques et les concepts ne sont pas en bijection.
 

Frege et la création d'un langage monosémique

Quand on parle de la polysémie en tant qu'un problème, un défaut, on pense inexorablement à Frege et son projet logiciste. En effet, comme le langage naturel possède la capacité de produire des sens non formalisables, cela entre a priori en conflit avec l’objectif de précision absolue des mathématiques.
 

Et cette imperfection du langage, c'est précisément la polysémie, une forme de plurivocité :

La connaissance, même dans un domaine hautement formalisé comme les mathématiques, passe inévitablement, au moins en partie, par le langage naturel. La solution proposée par Frege pour éliminer l’incertitude était donc de créer un langage formel monosémique, une idéographie.

Ce projet a néanmoins été soldé par un échec, au moins dans le sens où Frege l'entendait : le paradoxe de Russell avait, dans un premier temps, réduit à néant son projet. Russell a prouvé qu'on ne pouvait pas définir l'ensemble de tous les ensembles2 ce qui a provoqué la crise des fondements qui a conduit à l'axiomatique d’aujourd'hui. Cet exemple très parlant indique que, contrairement à une idée reçue qu'en maths tout n'est que rigueur, précision, et monosémie, il est en fait extrêmement difficile d'arriver à un langage formel à partir du langage naturel3.

La polysémie existe-t-elle en mathématiques ?

Peut-on alors, comme le prétend le titre de cet article, parler légitimement de la polysémie dans le langage mathématique, et si oui, si l'on peut en trouver des exemples, est-ce que cette polysémie est voulue, assumée, et donc considérée comme utile ?

Pour continuer à chercher une application possible de la notion de polysémie en philosophie des mathématiques, on préférera ici une définition pragmatique de la polysémie, c'est-à-dire une définition qui nous permet d'aller au-delà du linguistique, et vers le pragmatique :

Bien que l'effort de rigueur formelle réalisé au cours des siècles passés ait concouru à supprimer, autant que possible, l'ambiguïté du langage métamathématique, et en particulier de la polysémie inhérente au langage naturel, au moins dans la pratique du mathématicien, on observe à de nombreux endroits un usage assumé de la polysémie.

On trouve, par exemple, dans un manuel de logique pour les étudiants, des exemples de polysémie, comme dans cet extrait de Nour, David, Raffalli, Introduction à la logique, Dunod, 2019 :
 

Une même expression peut donc avoir deux sens différentes, et seul le contexte permettra de distinguer parmi eux. Et ceci n'est pas un incident isolé.

La polysémie des opérateurs

Un exemple de la polysémie en mathématiques est la surcharge des opérateurs, que l'on pratique naturellement depuis le primaire :

• le « + » (addition) est utilisé indifféremment sur les entiers, les rationnels, les réels, les matrices, les fonctions...
• le « x » (produit) est utilisé indifféremment sur les entiers, les rationnels, les réels, les matrices, les fonctions..., mais pourtant le produit matriciel, lui, n'est plus commutatif, ce qui montre qu'on se trouve réellement dans une situation analogue au langage naturel (et pleinement assumée).

Au contraire, il est à noter que dans le langage informatique Caml, par exemple, cette surcharge n'est pas acceptée : l'opérateur + (resp. -, resp. *) est réservé au type int (les entiers), et l'opérateur +. (resp. -., resp. *.) au type float (les nombres à virgule flottante).

La polysémie en topologie

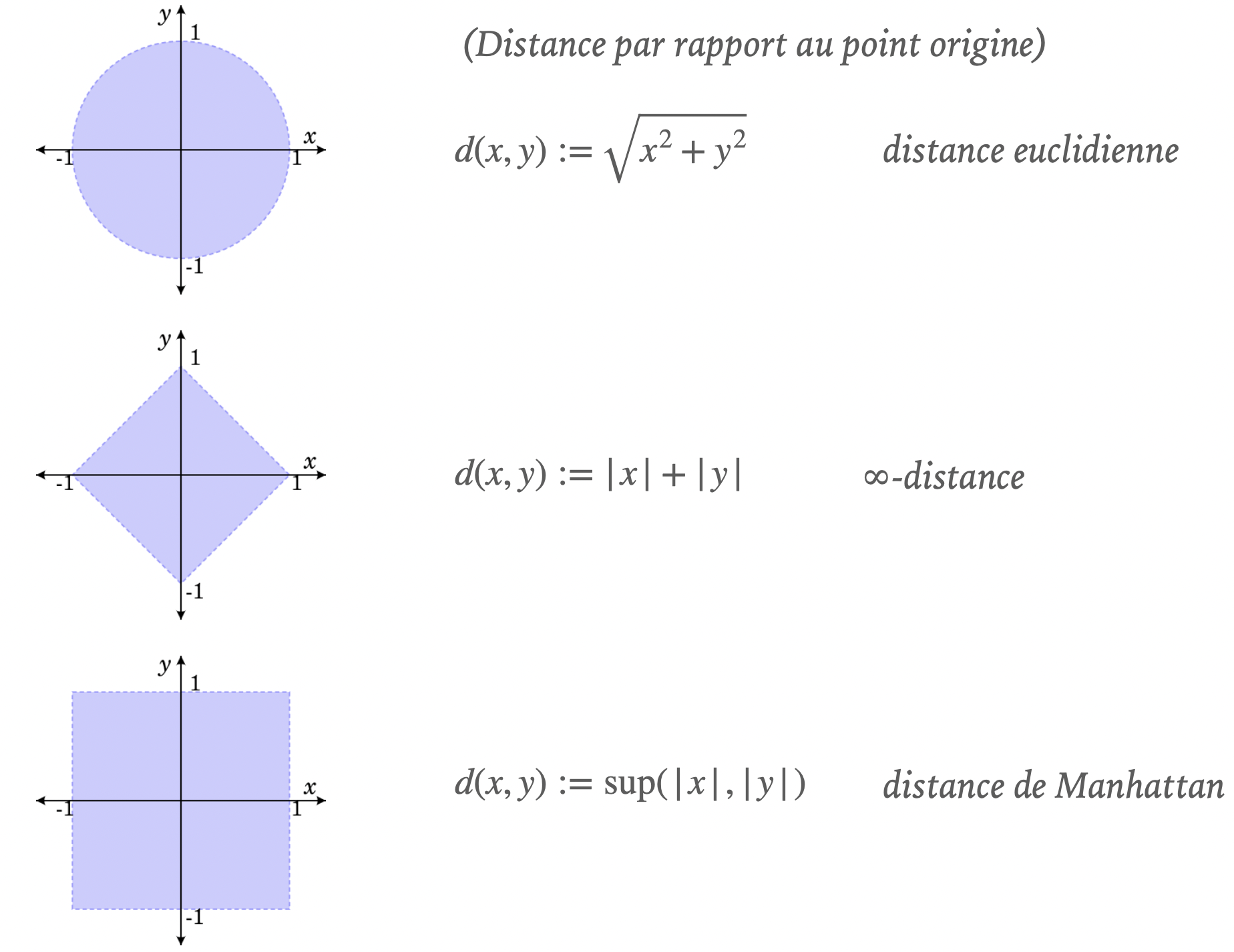
Un autre exemple de polysémie (volontaire) en mathématique, facile à visualiser (et qui étonne toujours les non mathématiciens car il est frappant dans son contraste même avec son origine tirée de la langue naturelle) est constitué par la notion de « boule » (de manière générale) ou, dans un cas particulier qu'on présente, du « disque » unité (de rayon 1), qui ne ressemble pas, en général, à un disque, mais peut même être ... un carré.

Cette polysémie visuelle prend naissance dans une autre polysémie, celle de la distance. On peut remarquer qu'il y a en effet, dans le monde réel, des distances différentes suivant les configurations : il y a bien sûr la distance du plus « court chemin » (en mathématique appelée la « distance euclidienne », mais aussi, si on fait le tour du monde en bateau, une distance calculée sur des arcs de cercle (ce qui est très différent : on ne peut pas traverser la terre !). Autrement dit, si on se déplace sur une sphère, la distance n'est pas celle de la « ligne droite ».

Les mathématiques ont formalisé cela en isolant trois propriétés qu'une distance devait définir :

• inégalité triangulaire,
• symétrie,
• séparation,

et toute fonction vérifiant ces propriétés est appelée ainsi.

Cela donne en particulier, dans le cas du disque, une infinité de variantes dont les plus courantes sont les suivantes :

La polysémie en géométrie

Au cours du XIX^e siècle on a découvert que l'acceptation ou non du 5^e postulat d'Euclide conduisait à différents types de géométrie :

• Géométrie euclidienne
• Géométrie sphérique
• Géométrie hyperbolique

Dans la géométrie sphérique, les « droites » correspondent visuellement à des cercles !

Pour s'assurer qu'il s'agit d'une vraie polysémie, car toutes ces géométries sont également valables, il suffit de lire Poincaré :

Les vertus de la polysémie dans un langage hautement formalisé

Pour apprendre un langage formel, on utilise du langage informel, ordinaire; similairement, les preuves formelles (au moins celles conçues par des humains dans un but mathématiques) ne naissent pas ex nihilo, elles commencent toutes comme preuves informelles. On n'apprend pas en langue machine, et notre représentation mentale et phénoménologique du symbole formel est générée par l'intersection de diverses représentations du langage naturel, toutes porteuses d'une polysémie intrinsèque, qui participe à la richesse des concepts et à la possibilité de chercher et d'inventer des choses nouvelles. On pourrait imaginer que la polysémie nourrit au minimum l'intuition et l'imagination du mathématicien quand il travaille sur un objet purement formel.

Pour conclure, voici un passage de Nicolas Bouleau qui incite à la poursuite de cette piste de recherche :

Ce n'est pas parce qu'on choisira des mots non-ambigus que l'on réduira l'incertitude. La polysémie est vertueuse car elle donne aux mathématiques ce qu'elle donne aux langues également : une très grande économie, à savoir la possibilité d'utiliser un nombre réduit de signes pour exprimer une gamme bien plus étendue de significations, mais aussi également la possibilité d'imager des concepts abstraits éventuellement sous-jacents pour mieux les comprendre et les représenter. Le fait d'utiliser les concepts déjà connus pour se rapprocher de ceux qui sont à découvrir est une loi du moindre effort positive, une optimisation du coût cognitif et un terreau propice pour l'imagination. Et si la polysémie devient localement gênante, on peut toujours la réduire, comme on a fait avec la résolution du paradoxe de Russell, alors que dans un cadre rigide et artificiel on ne peut rien tenter de plus, la pensée ne peut pas évoluer.

Nous dirons ainsi, pour répondre à la question-piège initiale, que la connaissance augmente l'incertitude, au moins en introduisant de nouvelles questions ; incertitude qui à son tour nous incite à augmenter notre connaissance : elle permet l'inférence et est donc motrice de ce processus dont on propose ici le caractère récursif (qui n’est pas sans rappeler la boucle entre le code (la polysémie) et l’innovation (la métaphore) qu’évoque Paul Ricoeur lorsqu’il écrit que « la métaphore prend appui sur un caractère du code, à savoir la polysémie ; c’est à la polysémie qu’elle vient en quelque sorte s’ajouter lorsque la métaphore, cessant d’être innovation, devient métaphore d’usage, puis cliché ; le circuit est alors bouclé entre langue et parole. »5 Nous ajouterions : tout comme entre la connaissance établie et la connaissance en cours de constitution, passant par l’indispensable crise d’incertitude qui engendre l’innovation.

(L’autrice tient à remercier vivement l’éminent linguiste M. René Rioul pour la relecture de ce texte et des commentaires fortement utiles)