Tire sur l'élastique, la mathématique cherra.
D'aucun verra dans l'allongement ou la contraction d'un chewing-gum des taux d'évolution, directs ou réciproques. Par exemple, +16% dans un sens ou -6,25% dans l'autre.
D'aucun jouera les experts en stéganographie, en inscrivant un message privé sur un strap bien tendu, puis en le relâchant : devenu secret le texte se cache dans les plis !
D'aucun déduira l'aire1 de l'ellipse de demi-axes $a$ et $b$, $\pi a b$, de celle du disque de rayon $a$, $\pi a^2$, d'une simple affinité.
Mais il y a plus sérieux, comme le montreront les deux exemples ci-après abordables en classes de spécialité Mathématiques au lycée 23.
De la densité de $\mathbb{Q}$ dans $\mathbb{R}$
Nous allons établir expérimentalement le résultat ci-après.
$\mathbb{Q}$ est dense dans $\mathbb{R}$
Entre deux réels distincts il y a toujours un rationnel.
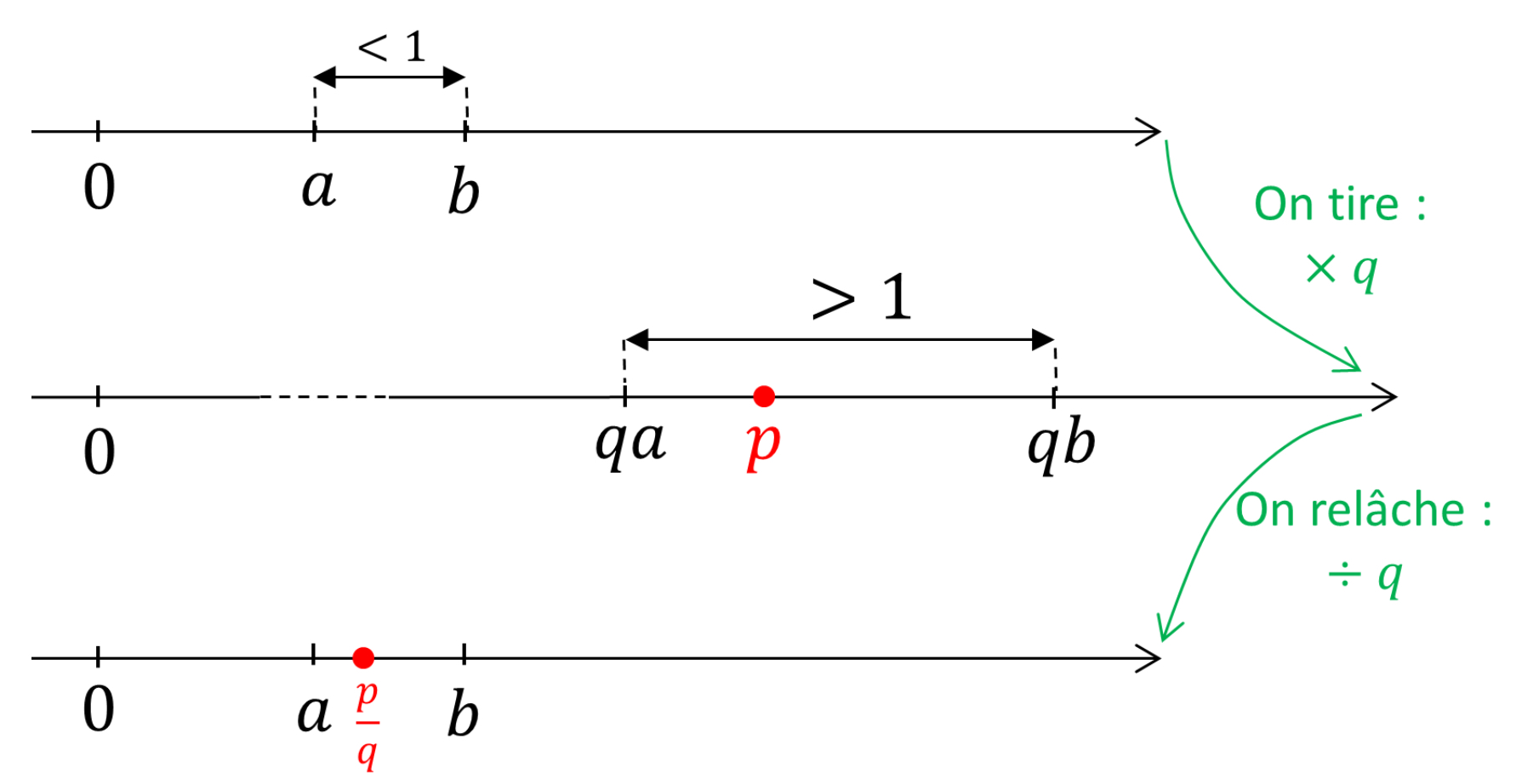
Soient deux réels $a$ et $b$ distincts, par exemple positifs. Que leur écart dépasse l'unité, et un entier (donc un rationnel !) s'immisce entre les deux.
Sinon... sortons-nous d'affaire grâce à un élastique (voir figure 1). Identifions-le au demi-axe réel positif ; marquons dessus $a$ et $b$ ; maintenons son extrémité gauche en 0 et tirons-le par la droite. Ainsi, étendons-le d'un facteur entier $q$ suffisant pour que l'intervalle entre les deux nouvelles marques, désormais $qa$ et $qb$, dépasse l'unité et capture donc un certain entier $p$. Relâchons l'élastique ; toutes les distances sont alors divisées par $q$ : en regagnant leur place, les marques $a$ et $b$ enserrent maintenant le rationnel $\frac{p}{q}$. Voilà la conclusion d'une méthode librement inspirée par une axiomatique qu'avait déjà posée, en son temps, Archimède4 5 !
De l'égalité $\mathrm{ln}(ab)=\mathrm{ln}(a)+\mathrm{ln}(b)$
Tous les chemins mènent aux logarithmes.
On peut d'abord construire l'exponentielle, avant de l'inverser — c'est la ligne désormais suivie par les programmes scolaires 23. Ou s'en remettre au calcul d'aires (sans même parler de calcul intégral !) — dans la continuité des grands problèmes de quadrature 6.
La vérité historique est sans doute plus complexe 76. Mais ces deux méthodes ont l'avantage de la concision. Et la seconde éclaire une propriété fort utile des logarithmes : transformer des produits en sommes. Pour la comprendre, nul besoin de technique. Nous travaillerons juste les fonctions comme une pâte à modeler 89. Il nous faudra seulement convenir, du reste aisément, du principe géométrique ci-dessous, déjà esquissé au collège 10 et que nous tiendrons pour acquis.
Plasticité des aires
Étirer (ou contracter) une surface plane dans une direction relativement à une autre (souvent, mais pas toujours orthogonale) d'un facteur $k$, $k>0$, multiplie son aire par le même facteur $k$. Noter qu'en doublant l'opération, dans une direction puis l'autre, on retrouve en particulier l'effet multiplicateur par le coefficient $k^2$ d'une homothétie sur les aires.
Notons $f_a:x\mapsto \tfrac{1}{x}$ et $f_b:x\mapsto \tfrac{1}{x}$ respectivement sur les domaines $[1;a]$ et $[1;b]$. Leurs graphes découpent chacun un morceau d'hyperbole équilatère. Étirons (ou contractons) celui de $f_b$ horizontalement, au point d'ajuster les abscisses de ses extrémités à $a$ et $ab$. Ceci déforme $f_b$ en $f_b(\tfrac{\bullet}{a}):x\mapsto f(\tfrac{x}{a})$ sur $[a;ab]$. L'aire sous la courbe, initialement égale à $\mathrm{ln}(b)$, en est multipliée par $a$ ; effet neutralisé quand on comprime (ou dilate) le tout verticalement du facteur $\tfrac{1}{a}$, figure 2.
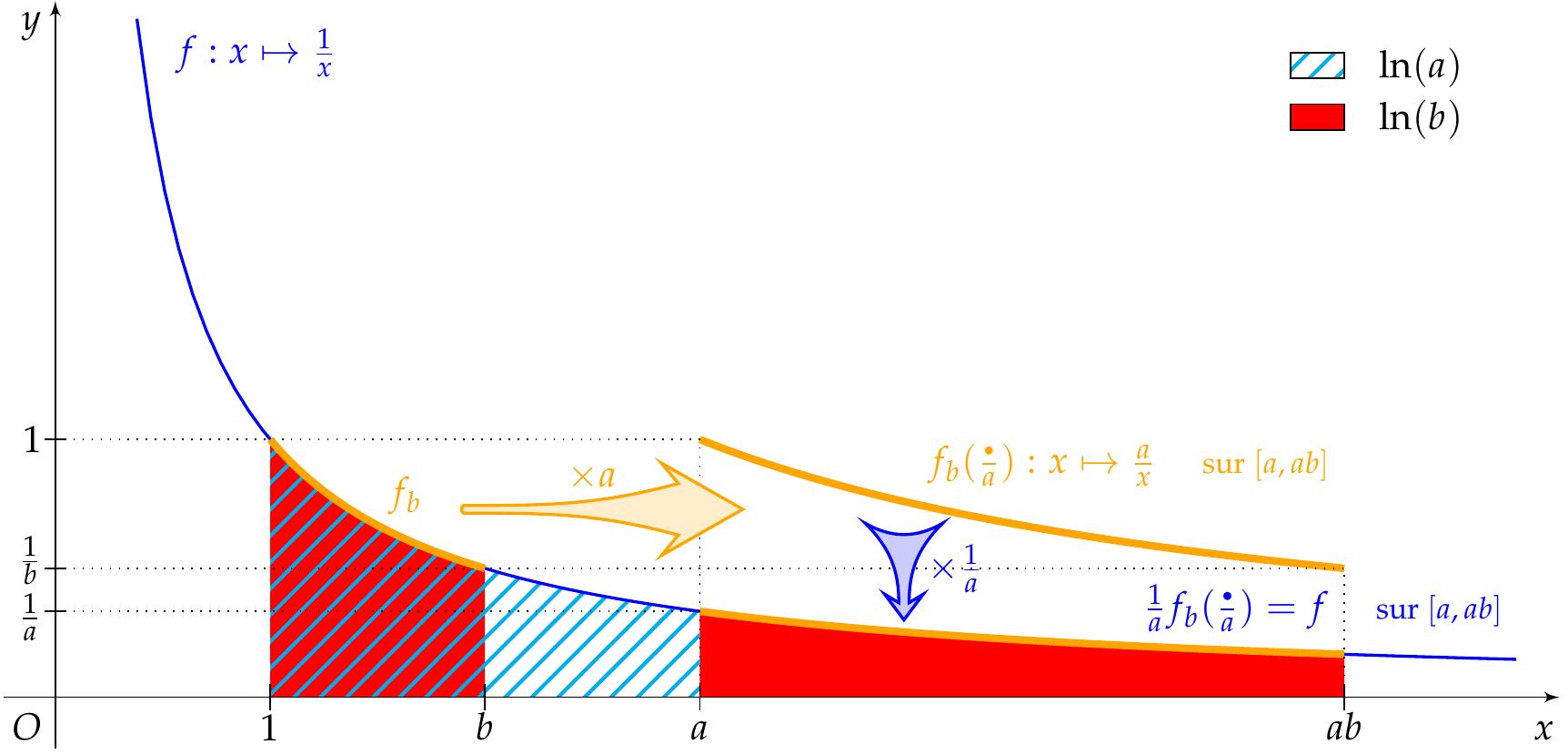
Ainsi, l'aire que délimite $\tfrac{1}{a} f_b(\tfrac{\bullet}{a}):x\mapsto \tfrac{1}{a}f(\tfrac{x}{a})$ de $a$ à $ab$ vaut-elle toujours $\mathrm{ln}(b)$. Mais $\tfrac{1}{a}f(\tfrac{x}{a})$ retombe sur $\tfrac{1}{x}$. Mis bout-à-bout, les arcs $f_a$ et $\tfrac{1}{a} f_b(\tfrac{\bullet}{a})$ recouvrent l'hyperbole sur le segment $[1;ab]$. En passant aux aires, on conclut à \[ \mathrm{ln}(ab) = \mathrm{ln}(a) + \mathrm{ln}(b). \] Suprêmes logarithmes, qui nous livrent cette formule « mirifique » aux dires mêmes de Néper11.




