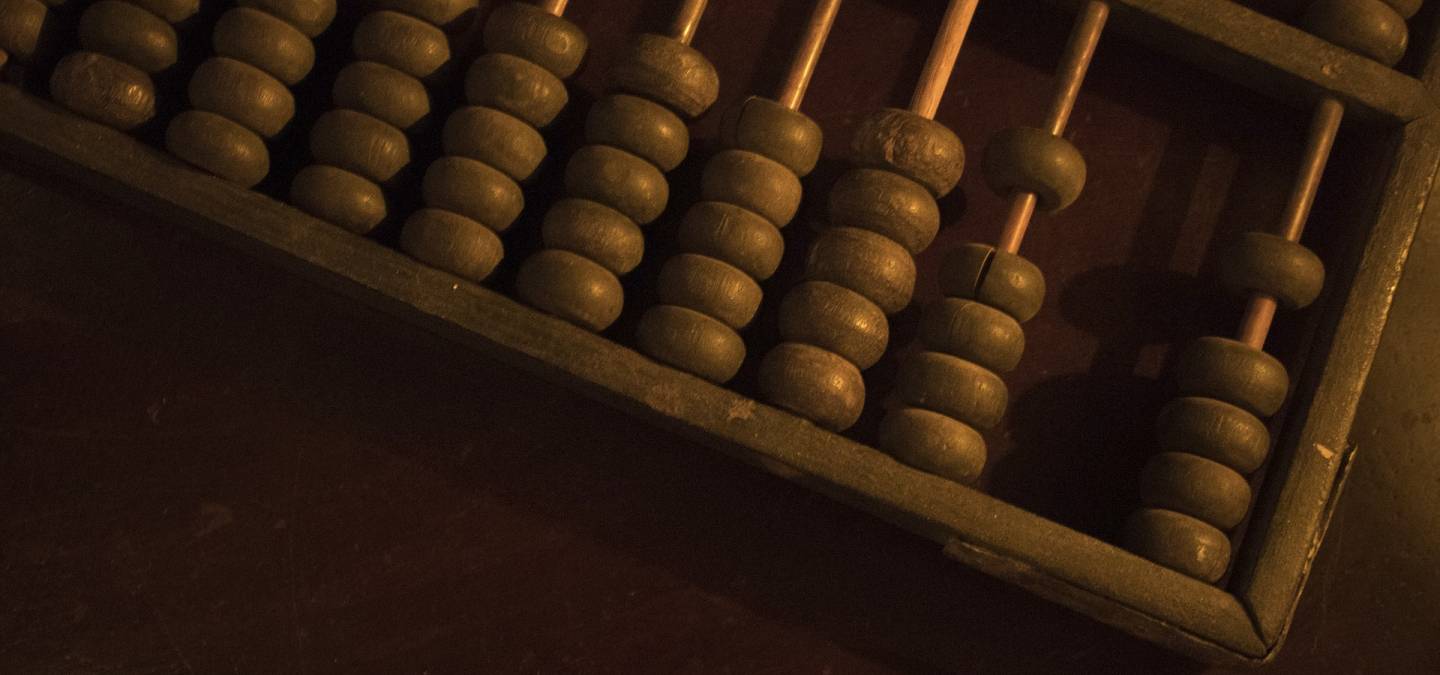Introduction

Les nombres font l’objet d’une fascination et les mathématiques sont souvent identifiées au calcul. Les stratégies pour mener à bien des calculs se sont affinées au cours du temps. D’abord les abaques, dispositifs munis de plusieurs rangs de pièces mobiles utilisés pour les calculs arithmétiques. Ensuite, les tables de valeur, qui ont lentement évolué vers des tables graphiques ou nomogrammes, c’est-à-dire un réseau de lignes ou de points donnant un résultat par simple lecture ou par un procédé de manipulation élémentaire. Ces savoir-faire se sont considérablement étendus jusqu’au milieu du vingtième siècle dans les domaines de la physique, de la finance, de l’architecture, et l’étude épistémologique des procédés sous-jacents a donné à cette discipline le nom de nomographie 1.

Ces outils mécaniques ou graphiques empiriques, basés sur des procédés mathématiques astucieux, nécessitaient des heures de pratique intensive durant lesquelles la vérification permanente des unités et de la cohérence des résultats étaient indispensables. Ils sont très rapidement tombés en désuétude à partir des années 1980 avec la montée en puissance des ordinateurs et le développement de la numérisation et de ses méthodes d’analyse. L’attention des professeurs, affranchis de la responsabilité de l’enseignement du calcul, a ainsi pu s’orienter sur le développement d’autres démarches et concepts.

Cependant, par le tragique principe des vases communicants de l’intelligence humaine, l’étirement en aval du champ des possibles offerts aux sciences a eu pour effet, en amont, une rupture du niveau de calcul chez les élèves. La disparition progressive de certains métiers artisanaux ou leur évolution, qui va de pair avec celle d’éléments familiers de l’ère mécaniste favorisant l’apprentissage par la manipulation et l’observation (pendule, balance…), a peut-être également contribué à ce recul. Il est par conséquent indispensable de bien distinguer l’intérêt des méthodes numériques dans l’ingénierie de celui de la maîtrise du calcul élémentaire, qui s’acquiert dès les premières années.

Cet exposé, découpé en trois parties, propose de recentrer l’attention des enfants sur quelques objets fondamentaux dont ils seront amenés à en découvrir l’intérêt et la richesse mathématique par une observation et une manipulation menées sur le long terme. Vous y rencontrerez des abaques et des nomogrammes, objets insolites et esthétiques qui suscitent la curiosité ou donnent envie d’être manipulés ou examinés2. Les intérêts didactiques sont entre autres de réconcilier le calcul et la vision géométrique afin de développer de façon empirique l’intuition mathématique de l’enfant dès le plus jeune âge. Cet article propose aussi de réfléchir verticalement aux opérations élémentaires induites par ces objets, c’est-à-dire d’analyser l’angle d’approche des opérations élémentaires que ces objets offrent et leur capacité à accompagner l’enfant d’une représentation naïve vers une modélisation plus abstraite. Dans cette première partie seront présentés des procédés qui permettent de construire chez l’enfant un univers mathématique qui donne du sens à l’addition et à la soustraction en les enracinant à l’aide de concepts de géométrie et de logique élémentaires.

Le sens des opérations élémentaires

L’addition

L’addition vue en tant que translation sur la droite numérique

a. « Un point plus un vecteur est égal à un point ». C’est probablement le premier contact intuitif de l’enfant avec la structure d’espace affine. Au jeu de l’oie, on représente la « droite » numérique sous forme spiralée, et la nouvelle position du pion est égale à l’ancienne plus la valeur du déplacement. Notons que cette approche introduit un élément de dissymétrie dans une opération qui, au départ, est symétrique, puisque l’addition est commutative.

b. L’intérêt du jeu de l’oie est de favoriser l’appréhension des grandeurs grâce à une frise numérique. Cela permet de développer une vision dynamique de l’addition à travers l’application d’une translation (lorsque la frise est une droite). Cette vision dynamique prépare à la notion d’opérateurs, puis de fonctions ($x\mapsto x + 7$ sur l’illustration ci-dessous)

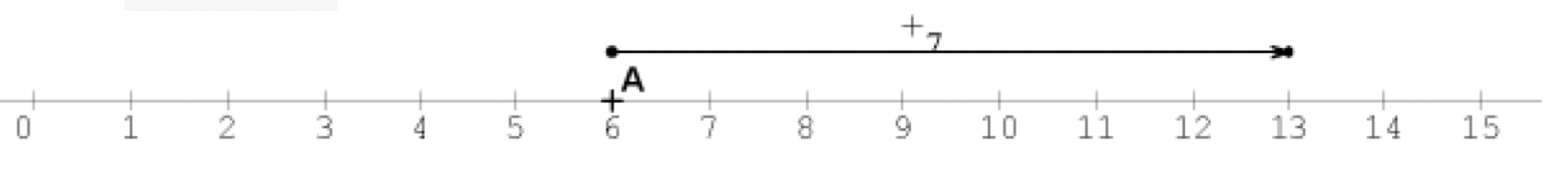
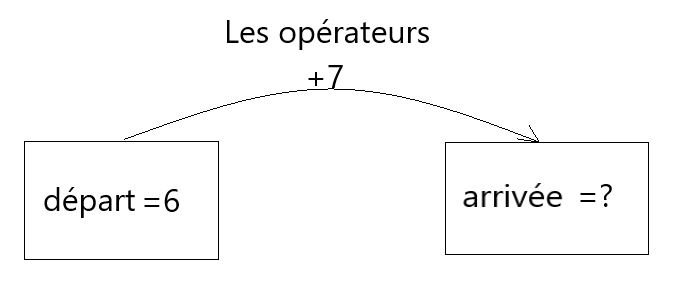
c. L’enfant qui débute au jeu de l’oie utilise l’addition itérative, de proche en proche en ordre croissant. Il se place sur la case 6, utilise la règle « je compte, je bouge », compte jusqu’à 7, et arrive à 13. Ceci se traduit algorithmiquement par :

dans S mettre 6
    pour i allant de 1 à 7
        dans S mettre S+1
    fin pour
afficher S

L’addition, vue en tant que fusion de deux tas. Illustration sur un boulier

a. La somme de deux nombres entiers positifs peut être également vue comme le résultat de la fusion de deux tas de grains. Il nécessite chez l’enfant la compréhension de la notion de conservation.

Illustrons ce principe de fusion sur un boulier, représentant le plus connu de la famille des abaques. Il en existe plusieurs types. En voici la version la plus simple, le boulier scolaire, qui est davantage un outil didactique qu’un outil performant :

b. Déroulement d’un calcul

Position initiale

Effectuons l’opération $263+574$. Pour cela, codons ces deux nombres.

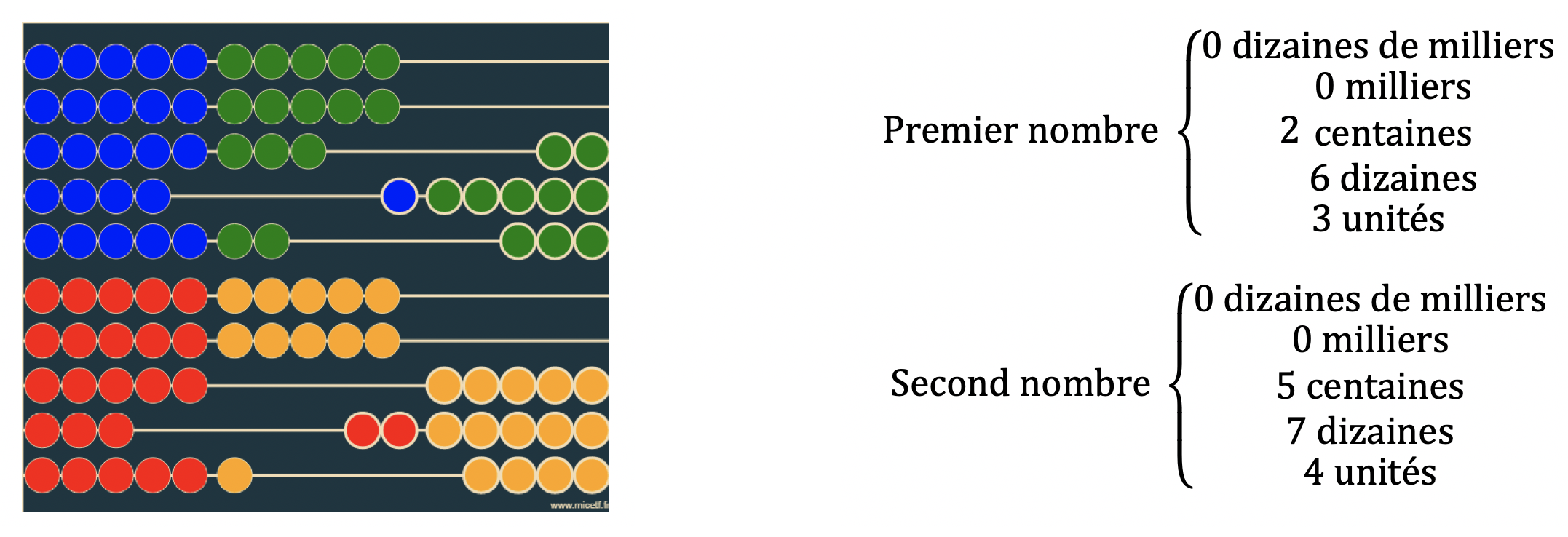
Le second nombre va progressivement se faire absorber par le premier nombre.

Première étape,les unités. Absorption des unités du second nombre. $$26\color{#49AEE9}{3}+57\color{#49AEE9}{4}=26\color{#49AEE9}{7}+57\color{#49AEE9}{0}$$

Deuxième étape,les dizaines.Nous allons diviser cette deuxième étape en 3 sous-étapes∶ → Le premier nombre ne peut absorber que 4 dizaines. $$ 2\color{#49AEE9}{6}7+5\color{#49AEE9}{7}0=267+(40+530)=(267+\color{#49AEE9}{4}0)+5\color{#49AEE9}{3}0$$

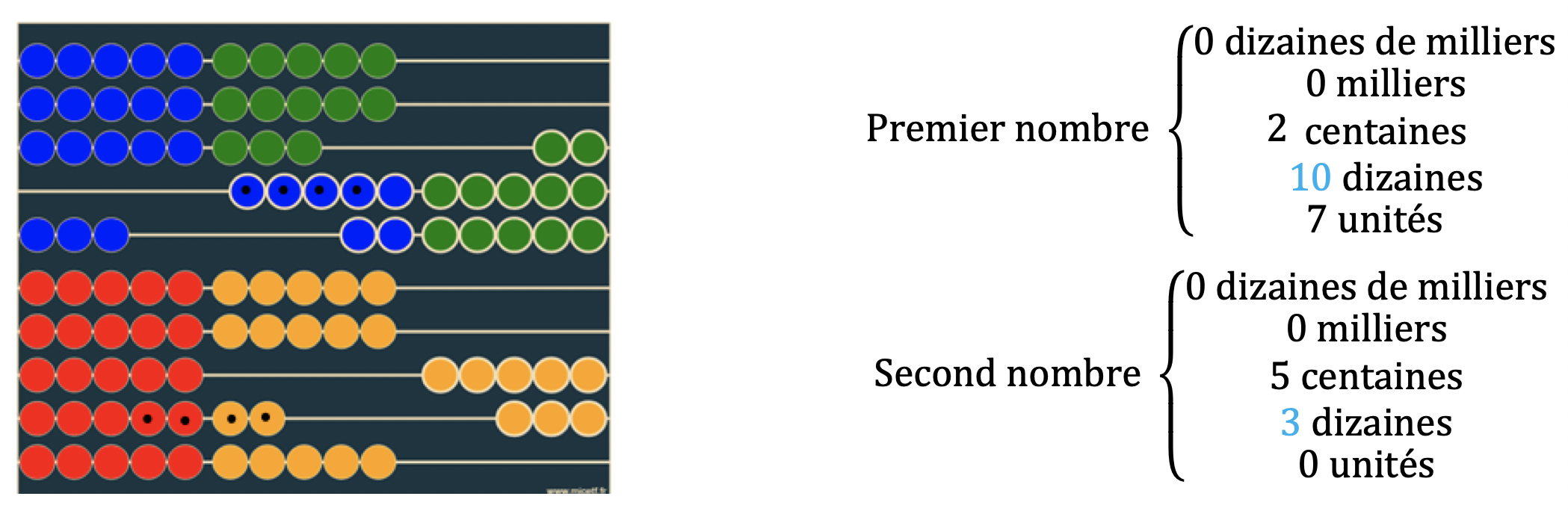
Le premier nombre gère sa retenue et transforme 10 dizaines en 1 centaine
$$(\color{#49AEE9}{26}7+\color{#49AEE9}{4}0)+530=\color{#49AEE9}{30}7+530 $$

→ Absorption des dizaines restantes du second nombre. $$3\color{#49AEE9}{0}7+5\color{#49AEE9}{3}0=3\color{#49AEE9}{3}7+5\color{#49AEE9}{0}0$$

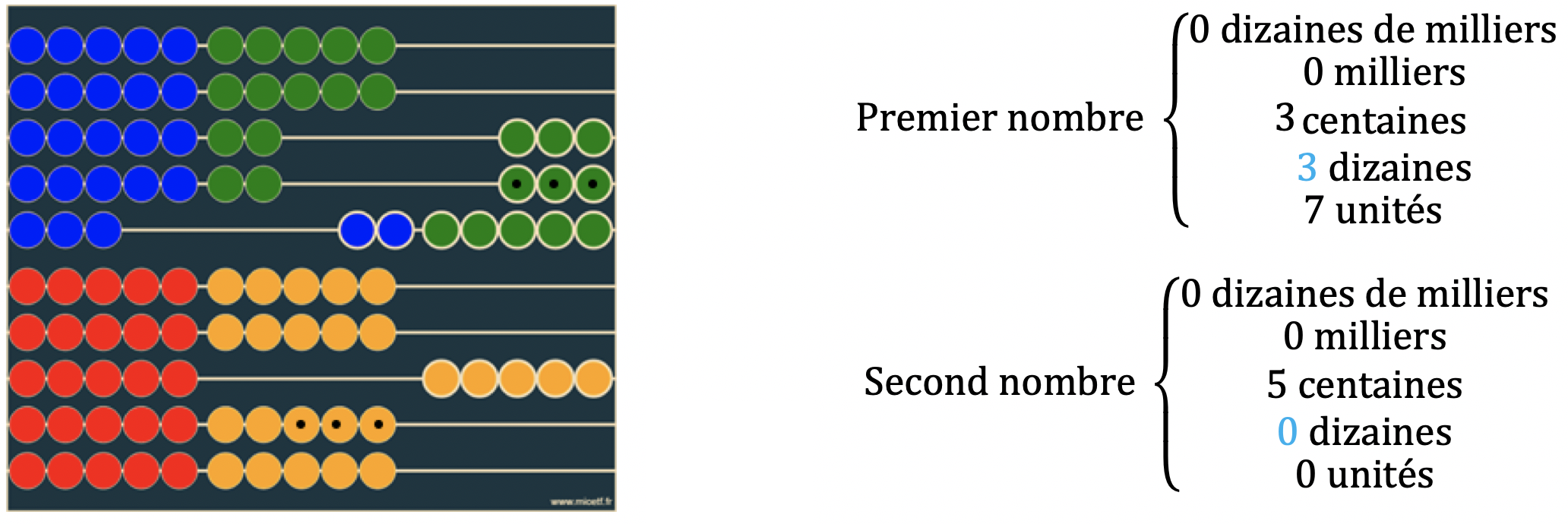
Troisième étape, les centaines. Absorption des centaines du second nombre. $$\color{#49AEE9}{3}37+\color{#49AEE9}{5}00=\color{#49AEE9}{8}37+\color{#49AEE9}{0}00=837$$

c. Analyse de la manipulation

1. On code chacun des deux nombres en base 10 sur le boulier, l’un en haut, l’autre en bas.
2. On utilise le principe des vases communicants en faisant coup par coup disparaître chacune des boules du nombre du bas, qui va être progressivement absorbé par celui du haut. A chaque unité –respectivement dizaine, centaine…- enlevée au nombre du bas, on augmente le nombre du dessus de la quantité correspondante.
3. Le nombre du dessus s’échange lui-même éventuellement sa petite monnaie (10 unités = 1 dizaine, 10 dizaines = une centaine …). Cet échange de monnaie est parfois nécessaire en cours de calcul.
4. L’algorithme prend fin lorsque le nombre du bas a été entièrement absorbé.

d. Interprétation et intérêts de la manipulation

1. Le boulier permet de représenter un nombre en base 10. 263, c’est 2 centaines, 6 dizaines et 3 unités
2. Il fait travailler de façon concrète les additions des quantités de même grandeur (ajouter les unités avec les unités, les dizaines avec les dizaines…). Cette prise en charge du sens des grandeurs pourra être très utile par la suite pour effectuer des calculs en sciences physiques et en vérifier rapidement la cohérence. Le sens de l’addition se diffuse du cerveau aux mains et réciproquement, dans une interaction du corps et de l’esprit, développant ainsi la mémoire kinesthésique. Les mouvements des mains s’effectuent pour l’addition de façon inversée sur le boulier : à mesure que la main droite effectue des mouvements vers la gauche pour enlever les boules, la main gauche effectue symétriquement les mouvements vers la droite pour conserver la somme invariante.
3. Le point le plus formateur est la gestion par la manipulation des problèmes de retenue (dix unités se troquent en une dizaine, dix dizaines en une centaine…). Ceci fait travailler la notion de base 10, développant ainsi le sens arithmétique des nombres.

e. Remarques

Voici le boulier chinois (suàn pan). A l’instar du système de numération des romains, ce boulier comporte sur la rangée du haut des quinaires (5), dizaines de quinaires (50)… Ce système des quinaires adopté par les chinois est, lui, adapté au calcul rapide. Pour le calcul rapide, on ne code pas les deux nombres, mais un seul, et on incorpore le second nombre directement (voir 2.1.1., principe de translation). On peut effectuer des additions, soustractions, multiplications, divisions, et même des extractions de racines carrées et cubiques !

Les japonais utilisent quant à eux un boulier légèrement différent appelé soroban. Il n’y a que 4 boules par colonne dans la partie inférieure et une boule par colonne dans la partie supérieure. La gestion des retenues s’effectue donc directement.

La commutativité de l’addition est une propriété qui semble apparaitre plus clairement lorsqu’on l’aborde sous l’angle de la fusion que sous l’angle de la translation affine.

f. Addition et projection

Une familiarisation précoce avec le boulier scolaire permet de développer chez l’enfant, via l’addition par absorption, une vision à la fois géométrique et récursive de la somme. La voici :

Le principe de fusion de deux tas peut être vu, avec un peu de recul, comme la lecture d’une image par projection. Pour lire le résultat de l’addition $S(m,n)$ — qui est bien-sûr égal à $m+n$ —, il suffit de :

1. Placer le point $M(m,n)$ sur le graphique.
2. Projeter $M$ sur l’axe $(Ox)$ parallèlement à la droite $(\Delta)$ d’équation $y=-x$.
3. Lire l’abscisse de $M$

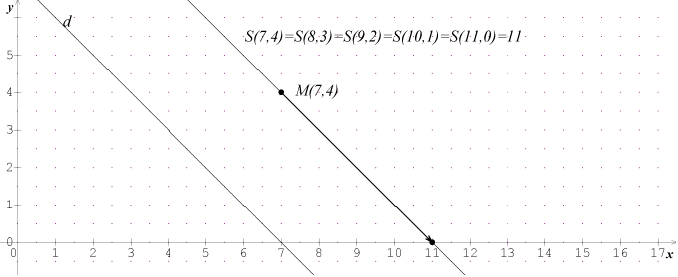
Pourquoi cette méthode fonctionne-t-elle ?

L’idée du principe de fusion est basée sur la propriété : \[ \forall (m,n) \in (\mathbb{N}^*)^2, \qquad S(m,n)=S(m+1,n-1) \quad \text{et} \quad S(m,0)=m \] et le résultat se prouve par récurrence sur l’altitude $n$. Le boulier prépare donc aussi au raisonnement récursif.

La soustraction

Différence et distance

a. La différence, vue comme opération réciproque d’une addition translative

1. Le saut inconnu pour aller d’un point à un autre

   La différence est introduite en tant qu’opération réciproque d’une addition. On connait à la fois :

   • → la case d’arrivée
   • → le déplacement ou la case d’origine.

   Il s’agit de déterminer la donnée manquante.

2. Notons que cette formulation masque une difficulté : en effet, le résultat d’une différence peut donc s’interpréter, du fait de la commutativité de l’addition, comme un nombre de départ ou un déplacement. Ce problème peut poser certaines difficultés aux enfants, notamment à ceux qui n’ont pas suffisamment développé l’addition en tant que fusion. Cette vision de la différence fait travailler la notion de réversibilité, stade de développement important chez l’enfant.
3. Représentation

   Imaginons donc que l’on connaisse le nombre de départ et le nombre d’arrivée, à savoir respectivement 6 et 13. Il s’agit de trouver la valeur du déplacement. \[6 + ?=13 \quad \Longleftrightarrow \quad ? =13-6\] par définition de la soustraction. La transposition dans le calcul littéral, qui est une étape clé pour la résolution d’équations, pose des problèmes durables à certains élèves. C’est pourtant une conséquence directe de l’addition vue comme une translation sur la droite numérique, cf. 2.1.1.

b. La structure métrique de $(\mathbb{R},| \ \cdot \ |)$ découle aussitôt de la notion de différence. On peut ensuite identifier la distance — usuelle — de $x$ à $y$ à la quantité $|x-y|$.

La soustraction, vue comme comparaison quantitative de deux tas

a. Avec un boulier, la soustraction s’effectue de façon analogue à celle de l’addition :

1. Codage des deux nombres, le plus grand en haut, le plus petit en bas.
2. On descend les boules du premier nombre en même temps que celles du second nombre qui lui correspondent tant que cette opération est possible. Dès que ce n’est plus possible :
3. On fait la monnaie sur le nombre du haut, en transformant si besoin 1 dizaine en 10 unités, 1 centaine en 10 dizaines … puis on applique l'étape précédente (2) jusqu’à ce que le nombre du bas soit nul. Au lieu d’être inversés, les mouvements des mains gauche et droite sont ici identiques.

Ce travail permet de préparer à la compréhension du bienfondé du système de retenues, qui n’est pas toujours facile à expliquer aux élèves.

Exemple. Voici un algorithme1 adapté au calcul de la différence 42-28 \[42-28=40-26=(30+10)-(20+6)=(30-20)+(10-6)=14\]

b. Soustraction et projection

 

 

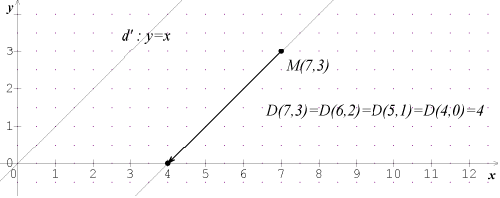
Le principe de comparaison quantitative peut être vu aussi comme la lecture d’une image par projection. Pour connaître le résultat de $D(m,n)=m-n$, il suffit de :

1. Placer le point $M(m,n)$ sur le graphique
2. Projeter $M(m,n)$ sur l’axe $(Ox)$ parallèlement à la droite $(d')$ d’équation $y=x$.

Cette construction fonctionne grâce à la propriété : \[\forall (m,n)\in \mathbb{Z}^2, \qquad D(m,n)=D(m-1,n-1) \quad \text{et} \quad D(m,0)=m \] Le résultat escompté s’en déduit par récurrence sur l’altitude $n$. Notons que ce principe permet facilement d’étendre la soustraction aux entiers relatifs.

c. Les difficultés sous-jacentes à cette soustraction par comparaison quantitative

La manipulation associée à une soustraction sur un boulier est très similaire à celle de l’addition et en aucun cas plus difficile, cependant son bienfondé est bien plus difficile à comprendre pour l’enfant. Pour que cette manipulation prenne un sens, il est nécessaire que l’enfant sache au préalable :

→ Comparer deux quantités d’objets ‐ que l’on matérialisera par exemple par deux tas de perles ‐ en enlevant simultanément une perle de chacun des tas, jusqu’à ce qu’un tas soit épuisé. Il s’agit d’une comparaison qualitative par récursivité : $\forall (A,B)\in (\mathbb{N}^*)^2,\qquad A\lt B \Longleftrightarrow A-1\lt B-1$

→ Comparer quantitativement deux quantités voisines, c’est-à-dire parvenir à exprimer le fait qu’il y a 1 perle de plus dans un tas que dans un autre si et seulement si, lorsqu’on épuise un des deux tas, il ne reste qu’1 perle dans l’autre.

→ Généraliser progressivement la constatation précédente à une différence de $2$, puis $3$, …

→ Le but étant d'arriver à la compréhension intuitive de cette formule ∶ \[ \forall(m,n,p)\in \mathbb{Z}^3, \qquad D(m,n)=D(m-p,n-p)\]

Un autre moyen d’y parvenir peut s’effectuer via le jeu de l’oie. Cette formule résulte du fait que la différence est invariante par translation, ce qui synthétise deux propriétés : la translation conserve à la fois les distances et l’ordre. Cette invariance peut s’assimiler en acceptant intuitivement le principe de récurrence : \[ \forall (m,n) \in \mathbb{Z}^2, \quad D(m,n)=D(m-1,n-1) \quad \Longrightarrow \quad \forall(m,n,p)\in \mathbb{Z}^3, D(m,n)=D(m-p,n-p)\]

Familiariser les élèves à la fois au jeu de l’oie et au boulier leur offre deux supports complémentaires qui s’avèreront très utiles pour une abstraction ultérieure. Cependant, les calculs de différence sur un boulier ne pourront être profitables, c’est-à-dire associés à la compréhension, que si l’enfant est déjà familier avec la comparaison quantitative, c’est-à-dire de formuler des phrases du type : « dans le tas $B$, il y a 3 perles de plus que dans le tas $A$ » et d’associer cette phrase aux calculs $B-A=3$ et $B=A+3$.

Dans la partie 2, nous incorporerons la multiplication et la division par le biais d’abaques moins connus.