La multiplication

Le groupement par paquets

La multiplication de deux entiers naturels est introduite en tant qu’itération d’additions.

Sa définition la plus naturelle est de la forme : \begin{equation} \forall (m,n)\in \big(\mathrm{N}^*\big)^2, \qquad m\times n = n+ n+ \cdots + n \quad \text{où le terme $n$ apparaît $m$ fois}. \end{equation}

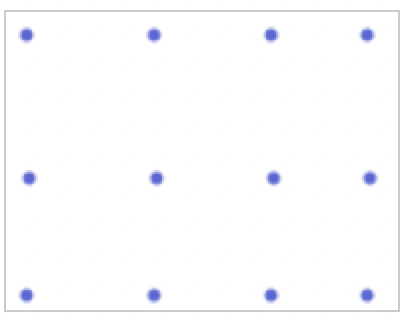
Il est clair, en inversant les lignes et les colonnes de la figure ci-dessus, que la multiplication est commutative.

Cette définition avec des pointillés étant peu satisfaisante, on lui préfère cette définition récursive : \begin{equation}\label{defrec} \left\{ \begin{aligned}\forall (m,n)\in \big(\mathbb{N}^*\big)^2 \quad P(n,m)&=P(n,m−1)+n \\ \text{et} \quad \forall n \in \mathbb{N}\quad P(n,0)&=0 \end{aligned}\right. \end{equation}

Représentation visuelle à l’aide de l’aire d’un rectangle

L’intérêt de la multiplication est d’éviter d’ajouter un grand nombre de fois le même nombre. Ainsi, pour que l’enfant adhère à l’utilisation de cet outil, il est nécessaire de présenter des problèmes pour lesquels l’addition devient sinon inadaptée, du moins lourde et fatigante. Ce n’est qu’ensuite que l’on pourra proposer à l’enfant de remplir lui-même la table de multiplications, en comptant le nombre total de petits carreaux compris dans la zone rouge ci-dessous, et en inscrivant le nombre dans la cellule en bas à droite du rectangle correspondant :

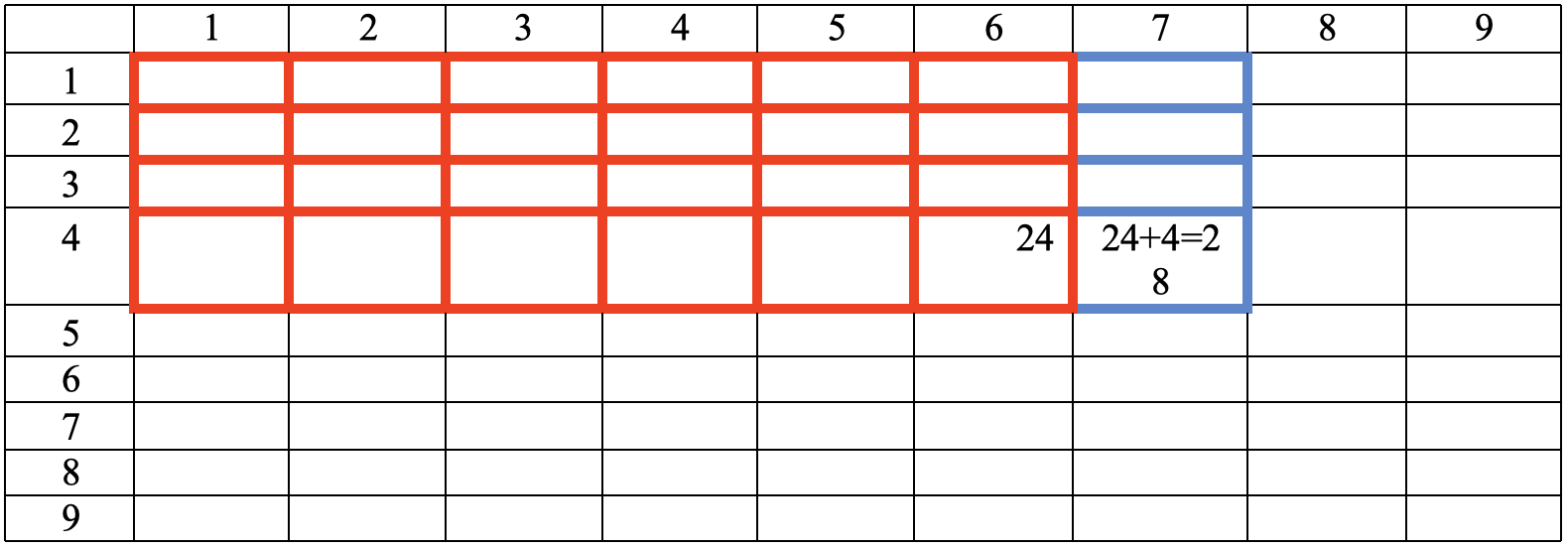
Avant de demander à l’enfant d’apprendre par cœur ses tables de multiplications, il peut être intéressant de lui donner ce tableau de multiplication vide, de lui laisser quelque temps pour le remplir, puis de lui demander de donner rapidement le résultat de certaines multiplications par simple lecture du tableau. Il est astucieux, pour remplir rapidement ce tableau, d’utiliser la définition récursive $\eqref{defrec}$.

En effet, $P(4,7)=P(4,6)+4=24+4=28$ , ce qui implique que l’on compte de $4$ en $4$ pour remplir la table de $4$.

Cet exercice présente en outre un intérêt particulier que nous allons découvrir.

La formule de la distributivité

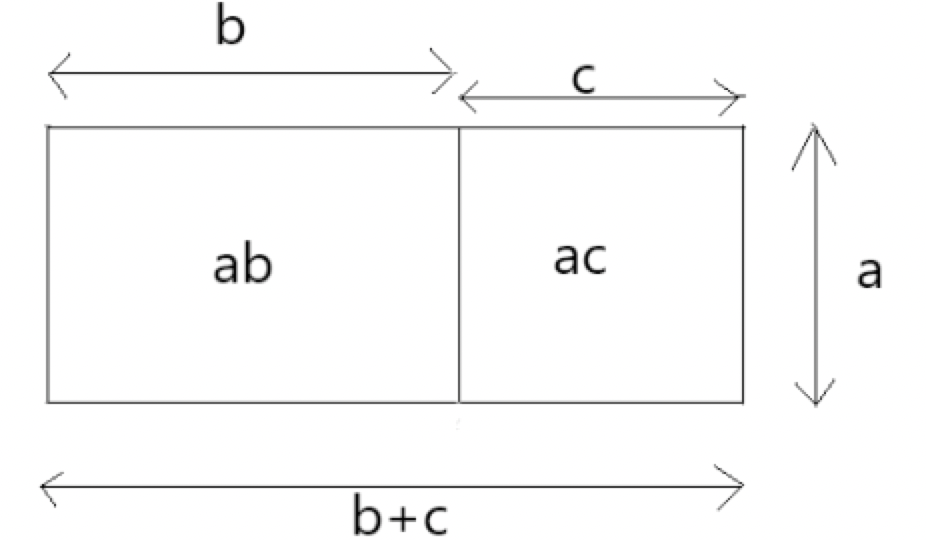
Cette formule est fondamentale. C’est une identité, c’est-à-dire une formule toujours vraie, dont l’énoncé est bien connu : $$\forall a,b,c \in \mathbb{R}^3,\ a(b+c) = ab + ac$$

Pour les nombres entiers positifs, cette formule découle par récurrence de la définition $\eqref{defrec}$.

Lorsque et sont des quantités positives, cette formule s’illustre à l’aide d’une figure :

Vers la multiplication posée

Derrière la technique de multiplication posée se cachent deux idées qu’il est indispensable de bien distinguer :

1. La multiplication par 10 transforme les unités en dizaines, les dizaines en centaines ... La pratique du boulier permet, en faisant la monnaie, d’intérioriser cette opération en faisant travailler la mémoire kinesthésique.
2. La formule de la distributivité, liée à l’aire d’un rectangle. Exemple: \begin{align*} 27 \times 32 = 27 \times (2 + 30) & = 27 \times 2 + 27 \times 3 \times 10 = 54 + 81 \times 10 \\ &= 54 + 810 = 864 \end{align*}

Il est intéressant de présenter les calculs de cette façon avant de se lancer dans la technique de la multiplication posée, qui, sans ces solides bases, s’apparentera à une recette mal comprise.

Une animation1 d’Alain Busser nous fait découvrir l’abaque de Gerbert d’Aurillac(~945−1003) qui permet d’effectuer des multiplications (voir troisième grand tableau) en séparant clairement la distributivité, la multiplication par 10, 100, 1 000 ... et le traitement des retenues.

La division, opération réciproque de la multiplication

Définition

La division peut être introduite de façon naturelle à partir du problème suivant : $$ 2 \times \ ? = 14$$

Le nombre manquant, que l’on appelle $14 ∶ 2$ ou encore $\frac{14}{2}$, est égal à 7.

On obtient donc $ 2 × \ ? = 14 \ \Leftrightarrow \ \ ? = \frac{14}{2} = 7 $

Ici encore, ceci prépare à la résolution d’équation.

Sens de la division d’une quantité

Une interprétation de la division est un partage équitable. Si le résultat d’une division n’est pas immédiat, il est intéressant de chercher la réponse par tâtonnement.

À noter qu’ici encore, nous avons la même ambigüité que pour la soustraction pour interpréter le sens d’une division. Dans ces problèmes de partage, il s’agit tantôt de déterminer la quantité attribuée à chacun des bénéficiaires, tantôt de déterminer le nombre de bénéficiaires.

Proportionnalité et recherche du coefficient multiplicateur

D’après ce qui précède, le coefficient multiplicateur, c’est-à-dire le nombre par lequel il faut multiplier une quantité de départ pour obtenir une quantité d’arrivée est donc : coeff mult = $\frac{\text{arrivée}}{\text{départ}}$.

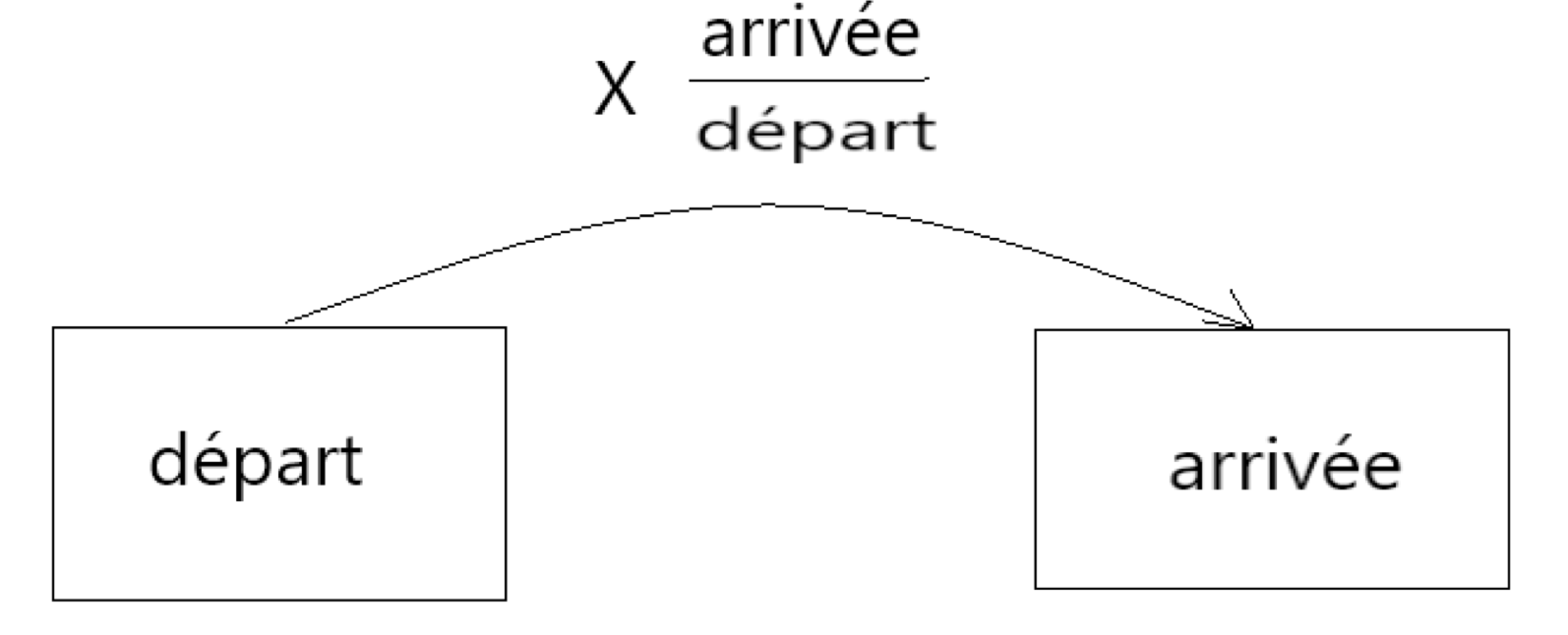
Proportionnalité et fonction linéaires : vers le théorème de Thalès.

• Derrière une formule savante, le théorème de Thalès décrit dans le triangle une propriété générale des formes qui peut s’énoncer ainsi :

  « Si deux polygones ont des formes similaires alors leurs longueurs sont proportionnelles. »

• Application : utilisation des fonctions linéaires pour effectuer des multiplications et divisions.

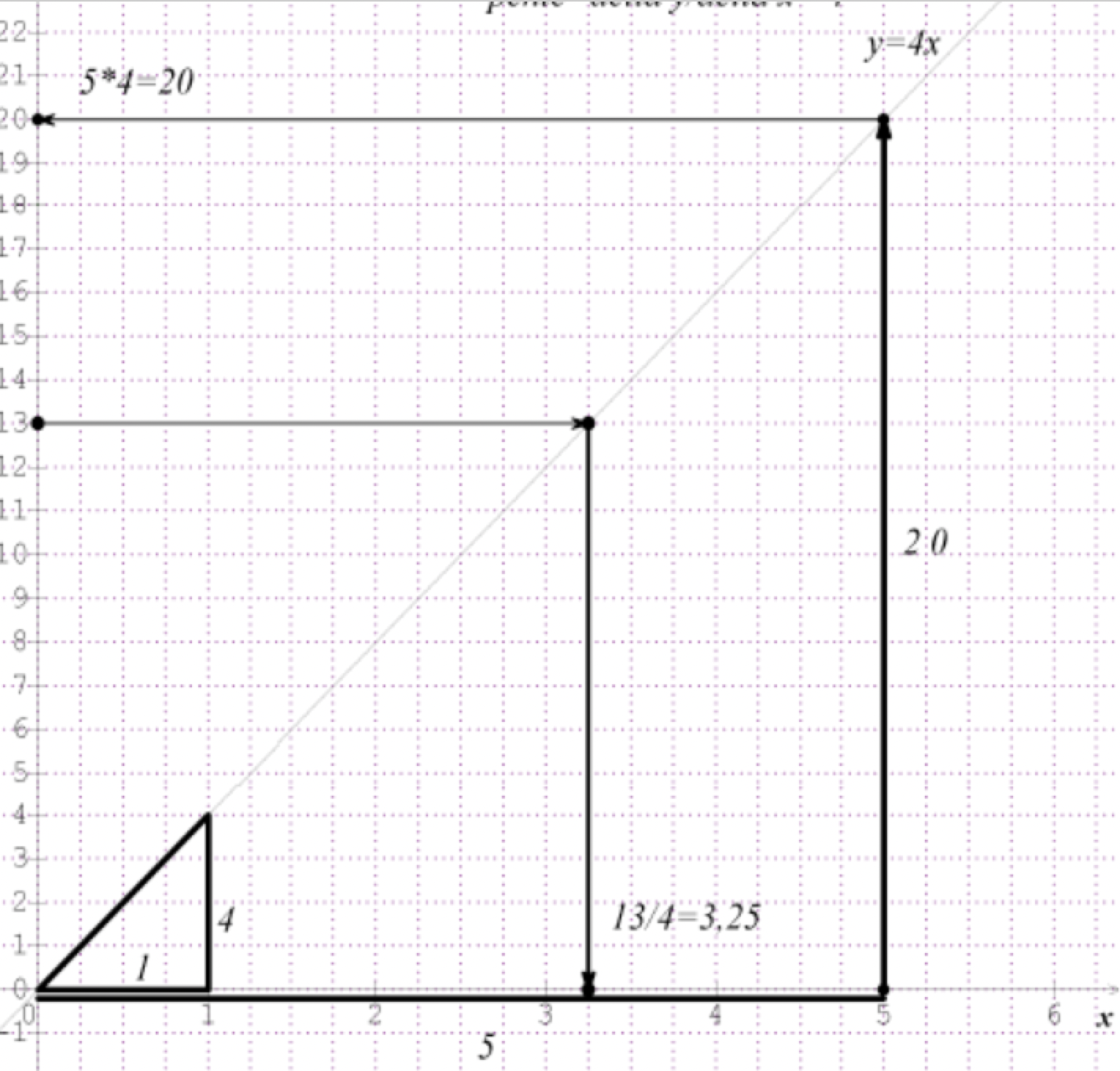
→ Pour lire le résultat 4 × 5, il suffit donc, d’après ce qui précède, de tracer la fonction linéaire $f ∶ x \mapsto 4x$ puis de lire l’image de $5$. Cette fonction peut alors s’interpréter comme « l’abaque qui multiplie par 4. »

L’intérêt de cette construction est de donner des valeurs approchées de multiplications décimales.

→ Pour lire le résultat $\frac{7}{4}$, il suffit de lire l’antécédent de $7$ par la fonction $f$ précédemment décrite. Lecture d’images et d’antécédents permettent de préparer à la notion de fonctions réciproques.

Division par 10 et nombres décimaux

(a) Par définition, $1,4 =\frac{14}{10}$ ; $2,76 = \frac{276}{100} $. Diviser un nombre par 10, 100 ou 1 000 revient donc à décaler la virgule d’un, de deux ou de trois crans vers la gauche.

(b)Division par 10 et théorème de Thalès. Voici un abaque de division par 10.

(c) Un nomogramme est un outil graphique de calcul constitué de courbes graduées entre lesquelles on place une règle. Ces outils se sont développés au XIX^e et au début du XX^e siècle. Ils sont aujourd’hui tombés en désuétude avec le développement de l’informatique.

Par exemple,les fonctions linéaires ont été utilisées pour lire les résultats de multiplications et de divisions décimales dans un nomogramme conçu par2 Léon, Louis Lalanne (1811−1892). Ce nomogramme a ensuite été progressivement remplacé par celui3 de Maurice d’Ocagne (1862−1938), moins coûteux en encre, qui utilise une échelle logarithmique.

(d) Vers la droite numérique des nombres réels Le principe décrit au (b) permet en théorie de représenter tous les nombres décimaux. L’inclusion réciproque est fausse. Le calcul de $\frac{10}{3} = 3,3333333 ....$, fraction qui se représente aisément à l’aide d’un procédé analogue, nous montre en revanche que tous les nombres constructibles à l’aide des deux nombres 0 ; 1 et de procédés géométriques ne sont pas décimaux. Ce problème de constructibilité des nombres à la règle et au compas a passionné les grecs. Ils ont prouvé que les nombres constructibles à la règle et au compas étaient exactement les nombres obtenus à partir des nombres entiers, des 4 opérations et des racines carrées. Par exemple, $\sqrt[7]{6 + 5/9}$ est constructible à la règle et au compas. Ce qui a eu des prolongements notoires au dix-neuvième siècle, avec la théorie des groupes alors naissante dans le sillage des travaux de Galois, par exemple avec la découverte du critère de constructibilité des polygones réguliers de Gauss-Wantzel.

(e) La représentation des fractions sur cette droite des réels

On représente l'ensemble des rationnels à partir de l'ensemble $\mathcal{F}$ des points à coordonnées entières d'un repère orthonormé dont l'ordonnée est supérieure ou égale à 1. Soient $I(1 ;0)$, $M(p ;q)$, $M'(p',q')$ ; $\theta_M=(\vec{OI}, \vec{OM})$ et $\theta_{M'}=(\vec{OI}, \vec{OM'})$. Puisque $\mathrm{cotan}(\theta_M )=\frac{p}{q}$, on observe la relation d'ordre : $$ \frac{p}{q} < \frac{p'}{q'} \Longleftrightarrow \theta_M > \theta_{M'} $$ Deux points situés sur une même demi-droite d'origine $O$ correspondent donc à un même nombre réel, et ce réel est le point d'ordonnée 1 situé sur cette demi-droite. Le problème de la recherche de la fraction de plus petit dénominateur contenue dans un intervalle se ramène donc à la recherche du point de $\mathcal{F}$ contenu dans un secteur angulaire dont la distance à l'origine est minimale. L'existence d'un tel point est garantie par la densité de $\mathbb{Q}$ dans $\mathbb{R}$. Cet abaque permet aussi de soustraire deux fractions et de donner le résultat sous forme de fraction irréductible (voir figure ci-dessus).

La droite numérique sur un cylindre

La génèse de cette représentation unificatrice

La structure métrique de $(\mathbb{R},|\cdot|)$

Nous avons vu que la droite réelle est munie d’une structure métrique qui permet de mesurer la distance entre deux nombres.

La structure arithmétique de $(\mathbb{Z},+,\times)$

a. Le choix d’une base pour compter

Le choix du nombre de chiffres utilisés dans la numération détermine la base dans laquelle on compte. De nos jours, c’est la base 10 qui est la plus répandue. Avant nous, les sumériens comptaient en base 60. Le pouce gauche comptait 12 phalanges, et les 5 doigts de la main droite servaient de retenue. Cette décomposition de $60=3\times 4\times 5$ est un bon point de repère en arithmétique, et a été retenue pour étudier les unités de temps et d’angles. L’horloge est d’ailleurs un excellent support pour travailler les fractions. La base 20 était quant à elle utilisée par les mayas4.

La base 2 est celle qui se prête le mieux aux opérations à l’aide de cet abaque5 inventé par John Napier, personnage dont nous reparlerons dans un troisième article. Sur cet abaque, les multiplications par 2 se traduisent par une translation d’une unité vers la gauche et les traitements des retenues peuvent être vues comme les règles d’un jeu de semailles6.

Cette base 2 a ensuite été utilisée pour effectuer les calculs des ordinateurs, car elle leur permet d’implémenter des opérations directement grâce aux composants électroniques. Les tables d’addition et de multiplication ne comportent que 4 cas possibles, ce qui a permis aux électroniciens Walther Bothe (1924) et Claude Shannon (1937) de développer des portes logiques utilisant l’algèbre de Boole (1815-1864), initiée par Leibniz (1646-1716). Ces portes logiques permettent ensuite à des fonctions logiques d’effectuer des calculs.

Pour effectuer un calcul entre deux nombres, l’ordinateur et la calculatrice codent chacun de ces deux nombres en base 2, effectuent le calcul à l’aide d’un algorithme simple et rapide, puis traduisent le résultat obtenu en base 10. Ce détour astucieux qui consiste, du point de vue de la machine, à traduire un message dans une langue familière (version), opérer dans cette langue familière (travail), puis enfin retraduire le résultat dans la langue de départ (thème) sera réexploité dans le paragraphe 4.1. sur les logarithmes.Mickaël Launay englobe cette conjugaison dans un concept plus vaste de changement de point de vue qu’il appelle « principe du parapluie »7. En langage imagé, il est parfois nécessaire d’ouvrir son parapluie pour éviter l’averse, d’effectuer son trajet sans encombres, et enfin de refermer son parapluie une fois le chemin parcouru.

b. Dès que l’on choisit une base, cela confère aux nombres des propriétés arithmétiques. Le tableau à double entrée qui suit permet de représenter les entiers de 0 à 99 et de découvrir certaines propriétés liées notamment aux tables de multiplication.

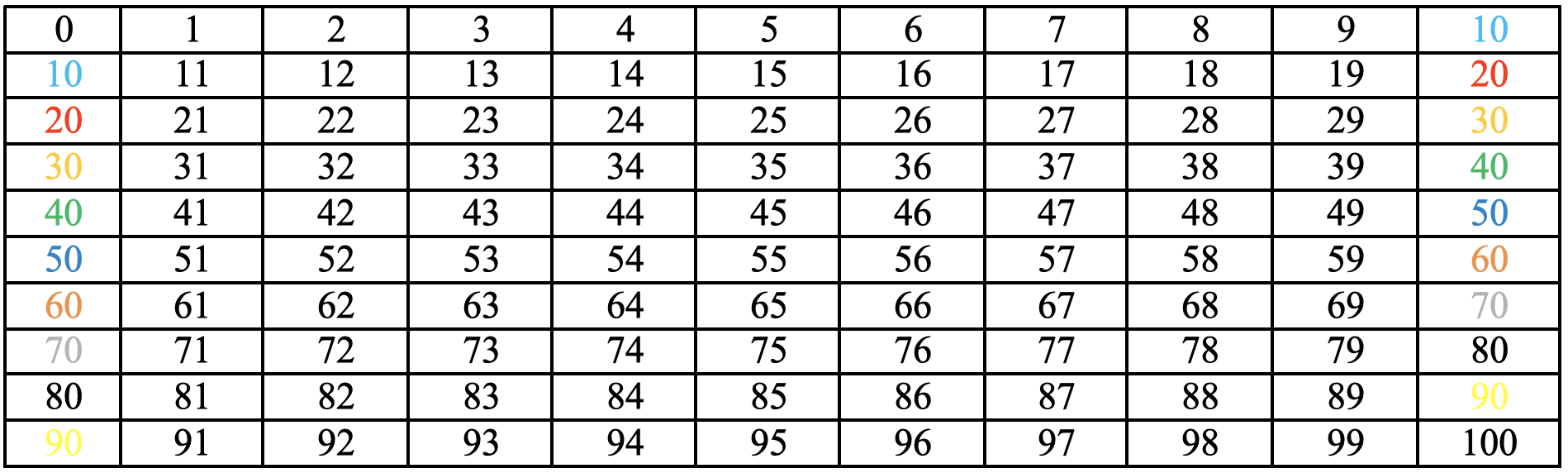
c. Le tableau ci-dessus est un excellent support pour découvrir l’alternance des pairs et impairs, certaines régularités dans les tables de multiplications, et par conséquent des critères de divisibilité. Une colonne supplémentaire a été ici ajoutée à droite de la grille didactique usuelle pour expliquer ce qui va suivre. Additions et soustractions sont liées à un programme de déplacement. Ajouter 1 revient à se déplacer d’un cran vers la droite, ajouter 10 revient à se déplacer d’un cran vers le bas. Pour les soustractions, on remplace « droite » par « gauche » et « bas » par « haut ». On rencontre cependant un problème de stabilité : ce procédé fonctionne tant que le point image par la translation est sur la grille.

Par exemple, pour ajouter 7, soit on se déplace de 7 crans vers la droite, soit on se déplace d’1 cran vers le bas et de 3 crans vers la gauche. On sent là les limites de la représentation du tableau à double entrée, qui nous contraint à gérer nous-mêmes le problème de la retenue lorsqu’on effectue la somme de deux nombres.

d. Pour régler ce problème de stabilité, on procède à une identification. Il s’agit donc d’identifier les nombres dont les couleurs sont identiques. Pour ceci, il suffit de coller ces nombres deux à deux.

Une représentation hélicoïdale de la droite numérique sur un cylindre

Le collage précédemment décrit aboutit à la représentation cylindrique donnée ci-dessous :

On représente la bande numérique sur le cylindre par le gros fil rouge. La distance de 2 nombres est la distance curviligne entre ces deux nombres, c’est-à-dire la distance en unités en suivant le fil rouge. Le chiffre des unités se lit en vue de dessus. Il est donné par la projection orthogonale sur le cercle passant par l’origine de la bande. Le chiffre des dizaines est déterminé par le nombre entier de tours effectués par le fil rouge depuis l’origine. Les fils plus fins permettent de lire les tables de multiplication.

Une ouverture vers la géométrie des surfaces

→ Dans le plan ou l’espace, par deux points passe une ligne droite et une seule. C’est le segment qui relie ces deux points. Appelons « segment » sur le cylindre tout ensemble de points qui, une fois le patron déplié, est un segment. Alors par deux points quelconques il passe une infinité de segments.

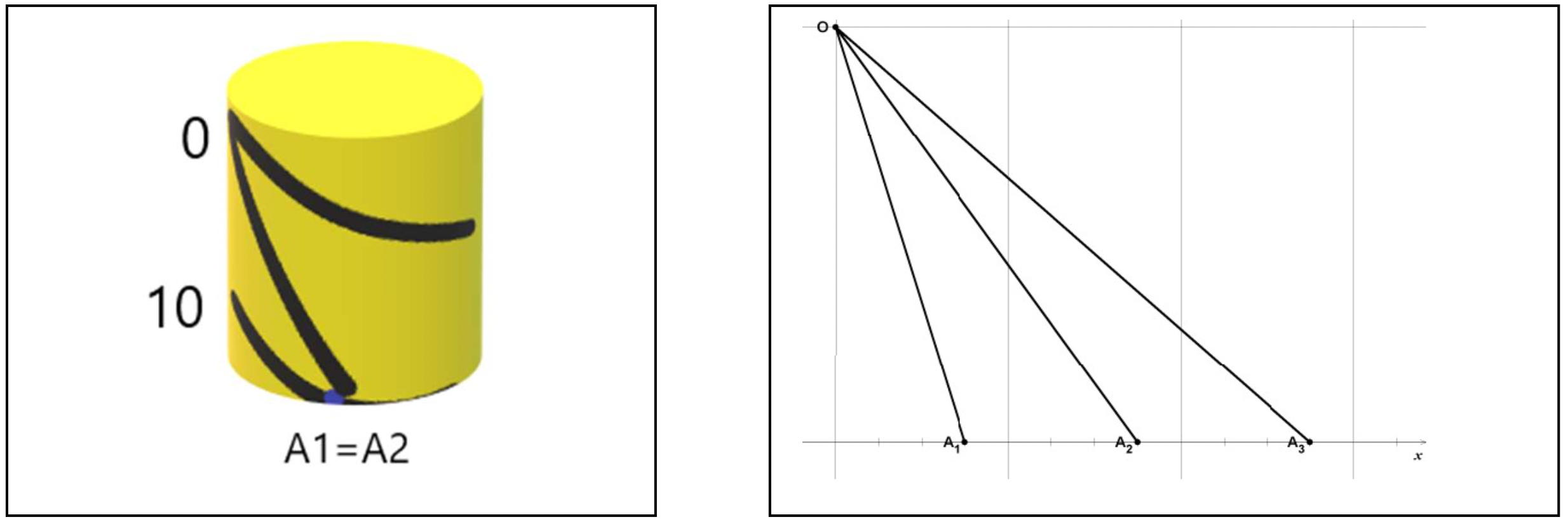
La représentation de la droite numérique sur le cylindre présente plusieurs intérêts

→ L'addition et la soustraction s'effectuent directement sans avoir à se préoccuper de la retenue. Par exemple, pour ajouter 28 :

• Soit on descend de 2 étages (= dizaines) puis de 8 marches (= unités)
• Soit on descend de 3 étages et on remonte 2 marches.

→ L'atout majeur de ce cylindre réside dans la multiplication, dont les tables s'obtiennent élégamment à l'aide des fils de couleurs plus fins en exploitant la propriété décrite dans la section précédente. On relie en effet 0 et n par un autre trajet que celui du gros fil rouge, ici en tournant dans l'autre sens. Les multiples de n seront exactement les abscisses des points d'intersection du gros fil rouge avec ce fil. Nous exploitons ainsi la stabilité de l'addition sur le cylindre. Ajouter un même nombre correspond toujours au même déplacement, quel que soit l'endroit où l'on se trouve. Ceci permet de développer encore davantage le sens arithmétique des nombres que le tableau à double entrée ; si on représente aussi la table de 2, on peut presque lire les nombres premiers. Construire l'objet pour s'en convaincre.

→ Voici une équation paramétrique possible de cette « droite » numérique :

Dans le repère orthonormé direct $(O; \vec{i}, \vec{j}, \vec{k})$,$$ \left\{ \begin{align*} x(t) &= \cos\left(\frac{360t}{10}\right) \\ y(t) &= \sin\left(\frac{360t}{10}\right) \\ z(t) &= t \end{align*} \right. $$ où $t \in \mathbb{R}$.

Ce paramétrage est conçu pour décrire un mouvement hélicoïdal − du grec hélix qui signifie spirale − c'est-à-dire la composée de mouvements de translation et de rotation, où les vitesses de translation et de rotation sont constantes et le vecteur de la translation dirige l’axe de la rotation. Pour l’équation paramétrique donnée ci-dessus, le cercle est de rayon une unité, la vitesse de rotation est d’un tour dans le sens trigonométrique toutes les dix secondes et la vitesse de translation d’une unité par seconde.

→ Les divisions euclidiennes sont particulièrement lisibles sur cet objet. Par exemple, pour déterminer le résultat de la division euclidienne de 35 par 8, on suit avec le doigt le fil noir des 8. Le quotient est alors le nombre de points d’intersection du fil des 8 avec le gros fil rouge (zéro non compris). La lecture du reste est ensuite immédiate en descendant le long du gros fil rouge.

→ Les diviseurs d’un nombre, du moins ceux qui sont compris entre 3 et 10, sont les nombres qui correspondent aux couleurs des fils qui « passent » par ce nombre.

Une ouverture vers la notion d’ensemble quotient

Cette notion est essentielle en algèbre, et l’élève la découvre en arithmétique lors de l’étude des congruences.

Par exemple, on s’intéresse au reste de 2035 dans la division euclidienne par 12. Sur la droite numérique habituelle, on part de l’origine et on effectue un nombre de translations – égal au quotient de l’opération précitée – du vecteur $\vec{u} (12)$ jusqu’au point le plus proche situé à gauche de $M(2035)$, à savoir $M_1 (2028)$. Le reste est la distance de ces deux points, à savoir 7.

On dit alors que 2035 est congru à 7 modulo 12, et on écrit que $$2035 \equiv 7 \mod{12}$$

Une idée plus géométrique est d’enrouler la droite graduée autour d’un cercle de périmètre 12 unités. On identifie ainsi les points $O(0)$, $A(12)$, $B(24)$… Lorsque l’on s’intéresse aux points à coordonnées entières sur ce cercle, on obtient un ensemble que l’on appelle $\mathbb{Z}/12\mathbb{Z}$. Cet ensemble comporte 12 éléments appelés classes d’équivalences, qui eux-mêmes sont les ensembles infinis

\begin{align*} \text{cl}(0) = \overline{0} & = \{ \ldots; -12; 0; 12; 24; \ldots \} \\ \text{cl}(1) = \overline{1} & = \{ \ldots; -11; 1; 13; 25; 37; \ldots \} \\ \overline{2} & = \cdots \\ \vdots \\ \overline{11}& = \cdots \\ \end{align*}

Par définition, on a donc $\mathbb{Z}/12\mathbb{Z} = \{ \overline{0}; \overline{1}; \ldots; \overline{11} \}$. Sur cet ensemble quotient, on peut définir des additions. Comment ? Pensez aux horloges !

Cette notion d’identification par collage est essentielle pour comprendre les ensembles quotients.

Dans le prochain article, nous réexploiterons cette idée de tendre un fil, non sur un cylindre, mais sur un cône tronqué, dont le cylindre est l’objet limite lorsque le rayon du petit cercle est égal à celui du grand cercle. Ceci ouvrira le théâtre des opérations aux logarithmes et aux exponentielles.