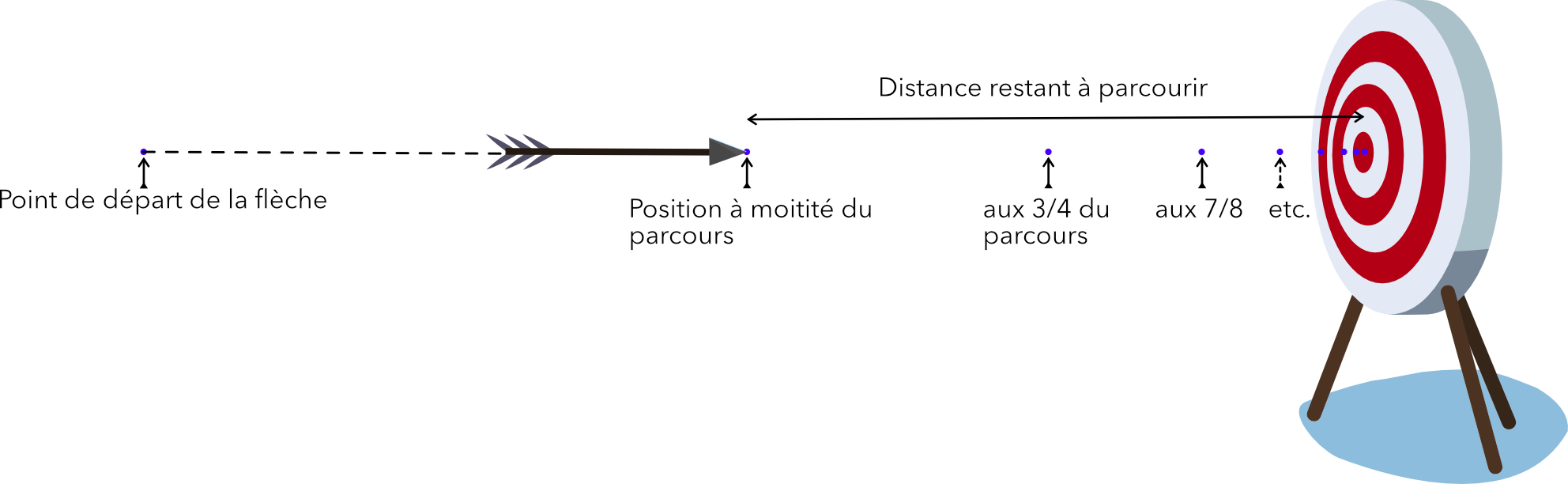
Zénon1 n'est qu'un menteur. À décocher la flèche qui n'atteint pas sa cible, pourtant mise à portée d'une volée, il hurle au paradoxe. Au nom de quoi, sauf en visant à côté ? Qu'à tout instant de la trajectoire, un écart même infime sépare la flèche de sa cible ? Puis la moitié de cet écart, puis la moitié de sa moitié ? Puis... Imposture ! Ce n'est pas le temps que dure la course qui prend l'éternité, c'est le temps pour la dire. Trêve de bavardage : confondre l'espace et le temps, là est le subterfuge. À ce compte, on s'interdirait de rallier $0$ à $1$ d'un trait de plume, freiné par chaque valeur intermédiaire — tant il y en a sur le chemin. Quel cinéma. Comme l'entêtant « jusqu'ici tout va bien » de l’homme qui se rassure, précipité d’une tour, mais dont la vie s’étire telle un chewing-gum à ses dernières secondes, millisecondes, microsecondes,... quand l’espace se resserre, inéluctablement 2.

Zéna, élève de CM2, a bien compris ces artifices.

Astucieuse, elle démonte les arguments de Zénon en les lui retournant. Si la flèche mesure, disons, trente centimètres, viendra bien le moment où, par un procédé dichotomique analogue, l'empennage arrivera à son tour à moins, mettons, d'1 cm de la cible. La pointe l'aura donc traversée (de 29 cm).

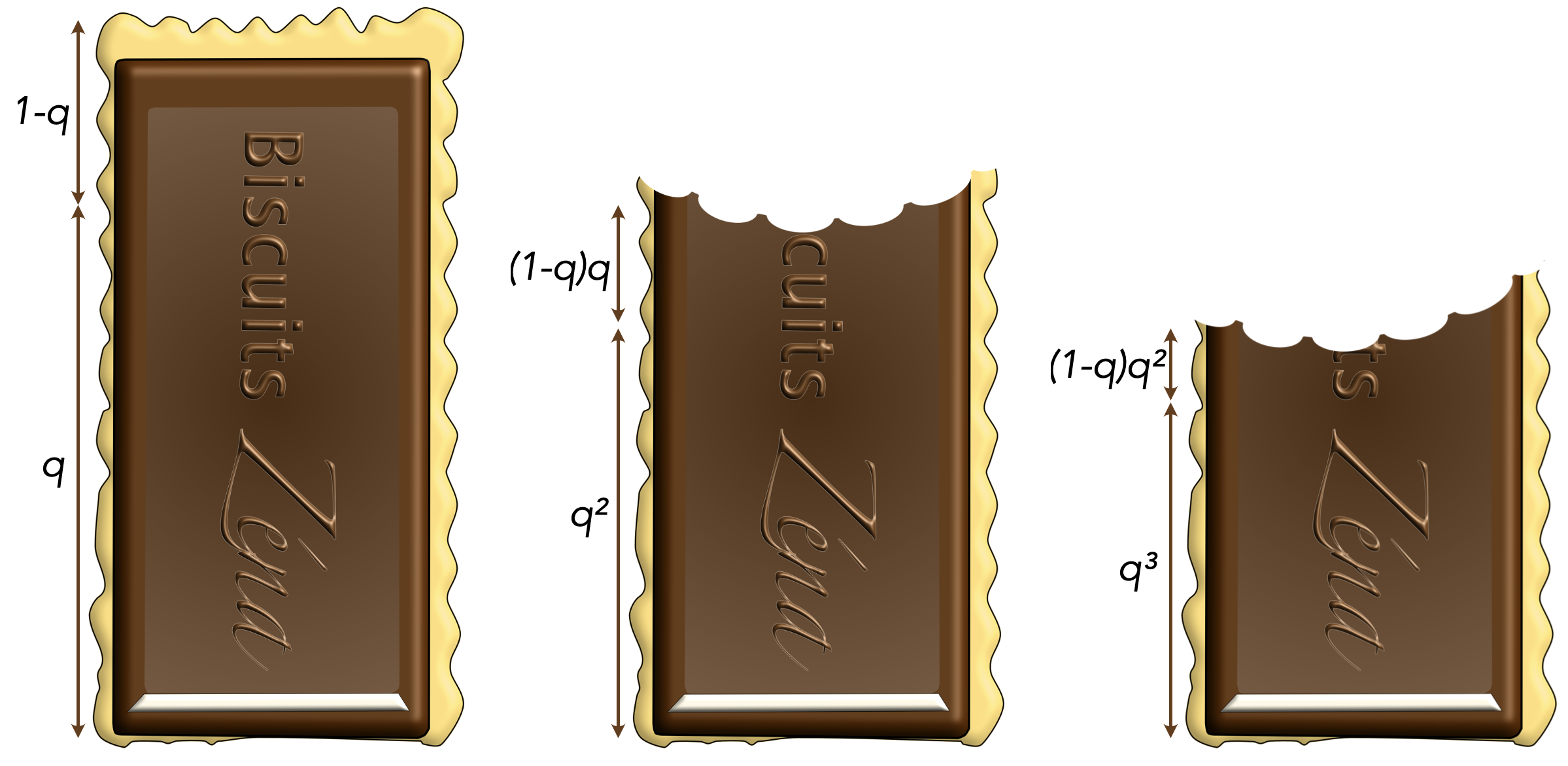
Espiègle, elle démontre chaque matin le vrai paradoxe, combien plus plaisant au petit déjeuner : réaliser une action authentiquement finie en un temps véritablement infini. D'abord, tremper la moitié du biscuit dans le bol de lait chocolaté. Apprécier. Ralentir, tremper la moitié de la moitié restante. Déguster. Ralentir, toujours. Maman peut klaxonner, papa peut s'emporter ; tremper la moitié de la moitié de la moitié restante. Savourer... Et, ce qui fonctionne avec des moitiés, fonctionne encore mieux avec des tiers, des quarts, ou toute fraction $q$ de l'unité puisqu'ainsi : \[(1-q)+(1-q)q+(1-q)q^2+(1-q)q^3+\cdots = 1\]

Que les parents de Zéna se rassurent ; à l'adolescence, c'est tout le paquet qu'elle croquera d'une bouchée !