On doit la réponse à cette question à Claude Shannon, mathématicien et ingénieur américain considéré comme le « père de l’âge de l’information ».

Son nom ne vous dit peut-être pas grand chose. Hollywood a glorifié d’autres héros scientifiques comme Alan Turing ou John Nash. Shannon, lui, a eu une vie rangée, modeste... et surtout ludique : adepte du monocycle et du jonglage, il s’est amusé à construire des machines plus ou moins loufoques : une souris qui apprend et retrouve son chemin dans un labyrinthe, une machine à jouer aux échecs, une autre à résoudre le Rubik's cube, une calculatrice en chiffres romains, un robot qui jongle avec trois balles, un bâton sauteur motorisé, et même une « machine inutile », qui dès qu’on l’allume, actionne une main pour s’éteindre elle-même... Dans le même temps, il a fait des avancées théoriques décisives dans des domaines aussi divers que les circuits logiques, la cryptographie, l’intelligence artificielle, l’investissement boursier et le wearable computing.

Mais surtout, Shannon créé la théorie de l’information en 1948, dans un seul article — A Mathematical Theory of Communication — le résultat de plusieurs années de recherche. Cette théorie révolutionnaire rassemble tellement d’avancées fondamentales et de coups de génie que Shannon est aujourd’hui le héros de milliers de chercheurs. On peut dire, sans exagérer, que c’est le mathématicien dont les théorèmes ont rendu possible le monde du numérique que nous connaissons aujourd’hui.

Décrivons plus en détail ses contributions les plus marquantes.

Le paradigme de Shannon

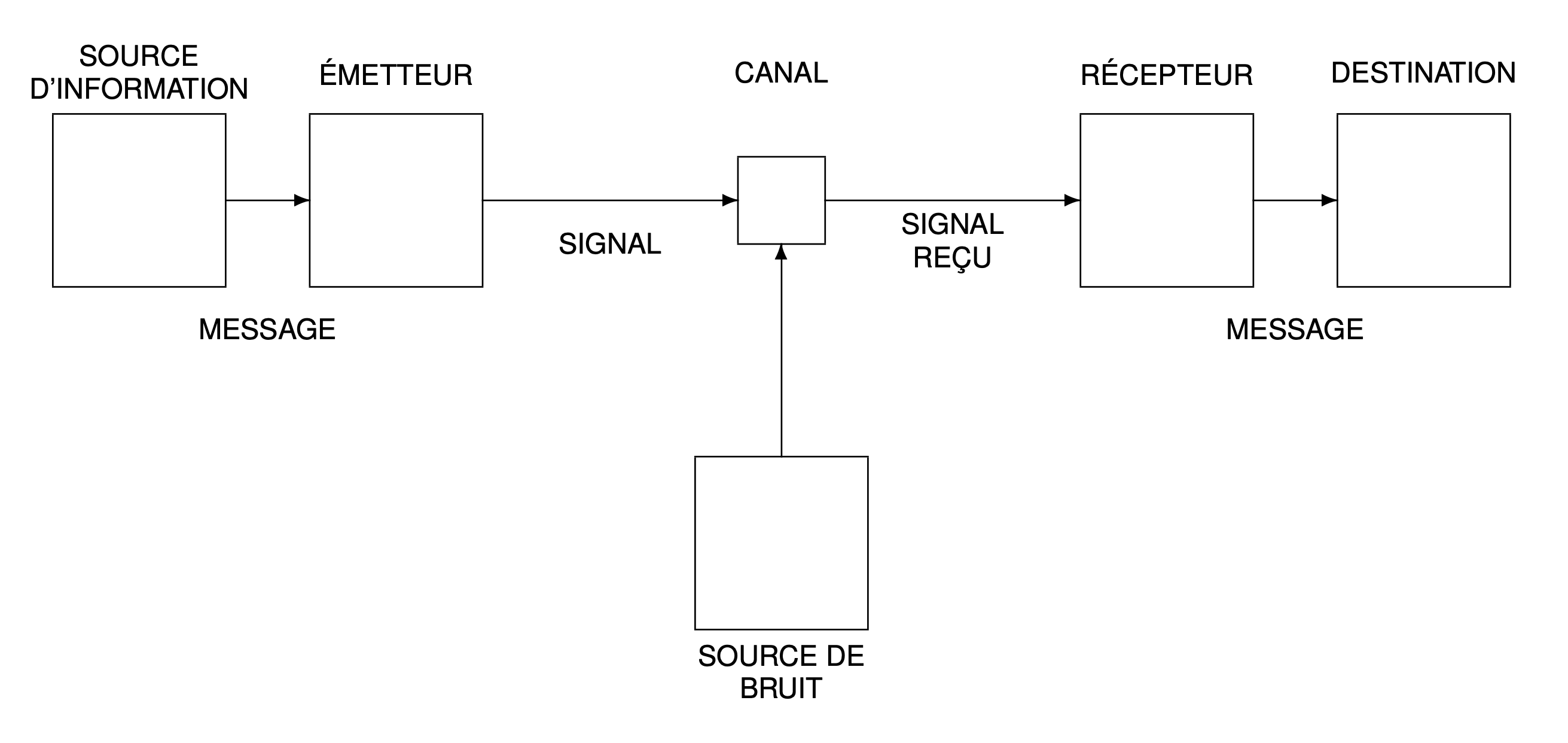
La figure suivante illustre le paradigme de la communication selon Shannon : un message émis par une source d’information est transmise dans un canal bruité puis reçu par le destinataire. Si un tel schéma peut paraître naturel aujourd’hui, il n’en était rien à l’époque : pour la première fois, on y distingue clairement les rôles de la source, du canal et du destinataire ; de l’émetteur et du récepteur ; et du signal et du bruit.

Ce paradigme est probablement la contribution de Shannon qui a eu le plus d’impact dans toutes les sciences, jusque dans les sciences humaines, en psychologie, en linguistique ou en sciences sociales. Dans les années 1950, la théorie est appliquée partout sans discernement, à tel point que Shannon, dans un éditorial intitulé The Bandwagon1 (« le train en marche ») met en garde contre les dérives d’une telle popularité.

L’aspect probabiliste

Le récepteur est incertain quant au message réellement émis, et Shannon considère donc ce message comme résultant d’un choix dans un ensemble d’alternatives, en laissant délibérément l’aspect sémantique de côté. Il introduit donc, pour la première fois, un modèle probabiliste pour toutes les variables en jeu dans la communication et fonde ainsi sa théorie sur le calcul des probabilités.

La théorie des probabilités venait de trouver sa forme définitive grâce à Andreï Kolmogorov quinze ans plus tôt. Ce dernier fut ensuite un ardent défenseur de la théorie de l’information. Au congrès international des mathématiciens de 1970, Kolmogorov déclare : « la théorie de l’information doit précéder la théorie des probabilités », et non l’inverse, et propose une approche algorithmique de la théorie de l’information comme fondement des probabilités !

L’unité Shannon

Il faut un chiffre décimal pour représenter 10 nombres, deux chiffres pour 100 nombres, trois pour 1000, etc. Représenter un parmi N nombres requiert $\log_{10}(N)$ chiffres décimaux, ou $\log_{2}(N)$ chiffres binaires, où $\log_{a}$ est le logarithme en base $a$. Shannon reprend l’idée exposée vingt ans auparavant par Ralph Hartley d’une mesure logarithmique de l’information, en privilégiant l’unité binaire.

Il popularise à cette occasion le terme « bit » qu’il attribue à John Tukey, comme contraction de binary digit (chiffre binaire, 0 ou 1). C’est l’idée révolutionnaire, devenue évidente aujourd’hui, que toute information peut être portée par des suites de 0 et de 1.

Mais le bit comme unité binaire d’information proposé par Shannon va plus loin que le simple chiffre binaire, car il prend en compte l’aspect probabiliste de l’information. Ainsi un bit aléatoire, c'est-à-dire une variable aléatoire de loi de Bernoulli, peut très bien porter une information qui est en fait inférieure à un bit ! En effet, dans le cas dégénéré ou la variable aléatoire vaut toujours 1, par exemple, l'information est nulle : il y a 0 bit d'information par bit. Ce n'est que dans le cas équiprobable où le bit aléatoire possède réellement 1 bit d'information.

Aujourd’hui, le bit d'information à une unité officielle qui s’appelle... le Shannon (sh).

Les limites de Shannon

Shannon énonce et résout le problème théorique de la communication. Il ne propose quasiment aucune solution pratique, mais établit des limites de performances, ce qui est au moins aussi important. Avant Shannon, des moyens de communication comme le télégraphe ont été développés pour ainsi dire dans le brouillard, sans le repère théorique permettant de savoir jusqu’où on peut aller. Avec Shannon, on sait que pour des ressources données, quoique l’on fasse, le meilleur système de communication fiable ne pourra jamais dépasser une certaine limite bien déterminée (et calculable) sur le débit d’information.

C’est comme si Shannon avait démontré la vitesse de la lumière sans dire comment construire la fusée qui pourrait s’en approcher. Bien sûr, cela a énormément stimulé la recherche de solutions pratiques permettant de s’approcher des limites de Shannon — un thème toujours important aujourd’hui.

Vers l’infini...

Les résultats de Shannon sont nécessairement asymptotiques : la recherche des limites optimales de performances passe par une analyse où la dimension des signaux tend vers l’infini. Une source d’information, par exemple, est représentée comme un processus — une suite de variables aléatoires $X_1, X_2, X_3,...$ représentant les symboles d’information émis au fur et à mesure du temps. Pour établir ses résultats, Shannon considère le vecteur $(X_1, X_2,...,X_n)$ où la dimension $n$ est arbitrairement grande.

Cette vision asymptotique permet non seulement d’exploiter les dépendances statistiques existantes entre les variables aléatoires, mais aussi d’obtenir un gain purement géométrique en grande dimension. Puisque $n$ tend vers l’infini, les résultats asymptotiques vont provenir de la loi des grands nombres, de sorte que les limites de Shannon sont établies comme des quantités moyennes. Le paragraphe suivant illustre cette approche dans un cas particulier.

L’entropie de Shannon

Considérons la source $\underline{X} = (X_1,X_2,...,X_n)$ pour une grande dimension $n$, où chaque symbole $X_i$ peut prendre un nombre fini de valeurs. Supposons, pour simplifier, que cette source stationnaire est « sans mémoire », c’est-à-dire qu’à chaque instant, un symbole est tiré indépendamment des précédents. Les symboles $X_1,X_2,...,X_n$ sont alors indépendants et identiquement distribués, et en notant $p(x)$ la probabilité qu’un symbole égale $x$, la probabilité $p(\underline{x})$ d’un message donné $\underline{x} = (x_1,x_2,...,x_n)$ est le produit des probabilités individuelles : $$p(\underline{x})=p(x_1)\cdot p(x_2)\cdots p(x_n).$$Regroupons les facteurs de ce produit suivant la valeur $x$ prise par chaque argument : $$p(\underline{x}) =\prod_x p(x)^{n(x)}$$où $n(x)$ est le nombre de symboles composantes du vecteur $(x_1,x_2,...,x_n)$ qui égalent $x$. Le rapport $n(x)/n$ est la fréquence empirique de $x$ qui, par la loi des grands nombres, tend vers $p(x)$ lorsque $n$ tend vers l’infini. Un vecteur $x$ « typique » tiré au hasard vérifie alors approximativement \[p(\underline{x}) \approx \prod_x p(x)^{n\,p(x)}=2^{-nH} \tag{1}\label{typiques} \]où $$H =\sum_x p(x)\log_2 \frac{1}{p(x)}$$est une quantité positive que Shannon appelle entropie par analogie avec l’entropie étudiée par Ludwig Boltzmann en mécanique statistique.

C’est en fait John Von Neumann qui recommande à Shannon d’utiliser le terme « entropie » car, lui dit-il, « personne ne sait vraiment ce qu’est l’entropie, de sorte qu’en cas de débat vous aurez toujours l’avantage » ! Par la suite, les relations qu’entretiennent l’entropie de Shannon avec la physique statistique ont donné lieu à d’innombrables débats et commentaires, notamment sous l’impulsion du physicien Léon Brillouin.

Le premier théorème de Shannon

La notion d’entropie et la relation $p(\underline{x}) \approx 2^{−nH}$ que l’on vient d’établir pour une suite $\underline x = (x_1,x_2,...,x_n)$ « typique » permet à Shannon de résoudre le problème théorique de la compression d’une source : il s’agit d’un cas particulier du paradigme de la figure 1 où le canal est sans bruit, et où l’on désire coder la source en la communiquant au destinataire d’une manière arbitrairement fiable avec un débit d’information minimal de sorte à comprimer au maximum la source.

Pour cela, il suffit de ne coder que les suites $\underline x = (x_1,x_2,...,x_n)$ typiques — c.-à-d. qui suivent approximativement la distribution de l'équation $\eqref{typiques}$ — car la loi des grands nombres que l’on vient d’utiliser implique qu’on ne peut tomber sur une suite non typique qu’avec une probabilité arbitrairement faible. En sommant la relation $p(\underline{x}) \approx 2^{−nH}$ sur toutes les suites typiques, on obtient la probabilité totale qu’une séquence tirée au hasard soit typique, qui est très proche de $1$ : $$1 \approx N \cdot  2^{−nH}$$où $N$ est le nombre total de suites typiques. On a donc $N \approx 2^{nH}$, soit $\log_2 N \approx n H$ bits d’information, d’où un débit de $(\log_2 N )/n \approx H$ bits par symbole de source.

Ce raisonnement peut facilement être rendu rigoureux et conduit au premier théorème de Shannon (pour le codage de source) qui affirme que $H$ bits par symbole suffisent pour comprimer fidèlement une source d’information. L’entropie apparaît donc être une borne inférieure sur le débit nécessaire pour coder l’information de façon fiable.

Ce théorème est asymptotique ($n$ tend vers l’infini) et ne donne aucun moyen de coder en pratique pour s’approcher de l’entropie. Mais Shannon — et, indépendamment, Robert Fano — ont l’idée de considérer un code à longueur variable où les symboles les plus probables sont codés par les codes les plus courts. Il est possible d’attribuer un nombre de bits légèrement supérieur à $\log_2 \frac{1}{p(x)}$ à chaque symbole $x$, de sorte que le débit moyen devient assez proche de $H$. Quatre ans plus tard David Huffman décrira l’algorithme optimal de compression dans ce contexte.

L’entropie relative

Une notion très proche de l’entropie de Shannon, développée au même moment et indépendamment en statistique mathématique par Harold Jeffreys, Solomon Kullback et Richard Leibler, est la divergence ou l’entropie relative entre deux distributions de probabilités $p$ et $q$, définie par : $$D(p,q)= \sum_x p(x)\log_2 \frac{p(x)}{q(x)}.$$Cette quantité est positive, comme on le démontre en utilisant la propriété de concavité du logarithme, et ne s’annule que lorsque les deux distributions $p$ et $q$ coïncident. Elle intervient naturellement dans le raisonnement précédent de Shannon : en notant $p′(x) = n(x)/n$ la fréquence empirique d’un symbole $x$, il est facile de vérifier qu’on a l’égalité rigoureuse : $$p(\underline{x}) = 2^{−nH(p′,p)}$$où $H(p′,p)$ est l’entropie croisée : $$H(p′,p)= \sum_x p′(x)\log_2 \frac1{p(x)}.$$Une suite « typique » $\underline{x}$ étant caractérisée par sa fréquence empirique $p′$, la probabilité de tomber sur une suite typique est égale à $$N\cdot 2^{−nH(p′,p)}.$$Si on remplace $p$ par $p′$, on obtient une autre probabilité qui est inférieure à $1$, d’où $$N\leq 2^{nH(p′,p′)}.$$Ainsi la probabilité de tomber sur une suite typique ne dépasse pas $$2^{n·(H(p′,p′)−H(p′,p))} = 2^{−nD(p′,p)}.$$Ce type de raisonnement est généralisable à d’autres ensembles que les ensembles de suites typiques, et le comportement exponentiel en $2^{−nD(p′,p)}$ est très utile en théorie des grandes déviations, ainsi que pour expliquer des comportements asymptotiques de tests d’hypothèses. Il conduit à une notion d’information de Chernoff (due à Herman Chernoff) pour classifier les données empiriques.

Par dérivation à partir de l’entropie relative, on obtient également l’information de Fisher (due à Ronald Fisher) utile en estimation de paramètres dans des distributions. La théorie de l’information trouve ainsi bien d’autres applications statistiques que celles liées au problème de la communication.

L’information de Shannon

Shannon décrit l’entropie $$H(X)=\sum_x p(x)\log_2 \frac1{p(x)}$$de la distribution de probabilité $p$ d’une variable aléatoire $X$ comme une mesure d’incertitude sur $X$. Il fonde également sa théorie sur une autre quantité $$I(X;Y)= \sum_{x,y}p(x,y)\log_2 \frac{p(x,y)}{p(x)p(y)}$$que Fano nomme information mutuelle entre deux variables $X$ et $Y$. C’est exactement l’entropie relative $D(p,q)$ entre la distribution $p(x,y)$ conjointe de $(X,Y)$ et la distribution $q(x,y) = p(x)p(y)$ qui correspond au cas où $X$ et $Y$ sont indépendantes. Elle est donc positive et ne s’annule que dans le cas de l’indépendance. Elle est également symétrique : $I (X ; Y ) = I (Y ; X )$ et mesure la quantité moyenne d’information entre $X$ et $Y$ (qui, naturellement, s’annule dans le cas où $X$ et $Y$ sont indépendantes).

Shannon écrit $I(X;Y )$ sous la forme $$I(X;Y)=H(X)−H(X|Y)$$où $$H(X|Y)=\sum_{x,y} p(x,y)\log_2 \frac1{p(x|y)}$$est l’entropie de la distribution conditionnelle $p(x|y)$, qui mesure l’incertitude sur $X$ connaissant $Y$. Cette dernière est inférieure à $H (X )$ puisque $I (X ; Y ) \geq 0$ : ainsi la connaissance (de $Y$) réduit l’incertitude (sur $X$), d’une quantité précisément égale à l’information $I (X ; Y )$ qu’apporte $Y$ sur $X$.

Ce type de raisonnement intuitif a excité l’imagination de nombreux scientifiques. C’est la première fois que le concept — jusque là flou — d’information transmise dans un système trouve une théorie rigoureuse. Le diagramme ensembliste ci-dessous résume les relations entre les différentes quantités utiles en théorie de l’information.

La méthode du « codage aléatoire » de Shannon

Considérons, toujours pour une grande dimension $n$, un canal bruité d’entrée $\underline{x} =(x_1,x_2,...,x_n)$ et de sortie $\underline{y} =(y_1,y_2,...,y_n)$ (bruité signifie simplement que la sortie $\underline{y}$ n'est toujours égale à l'entrée $\underline{x}$). Ce canal est décrit par les probabilités conditionnelles $p(\underline{y}|\underline{x})$ de la sortie connaissant l’entrée. Supposons, pour simplifier, que ce canal stationnaire est « sans mémoire », ce qu’on traduit par un développement en produit de probabilités conditionnelles individuelles : $$p(\underline{y}|\underline{x})=p(y_1|x_1)\cdot p(y_2|x_2)\cdots p(y_n|x_n).$$L’entrée du canal est le « code » portant l’information à transmettre. Shannon a l’idée géniale de considérer simultanément l’ensemble de tous les codes possibles que l’on peut utiliser dans la communication, comme si chaque code $\underline{x}$ était choisi au hasard selon une distribution $p(\underline{x}) = p(x_1) \cdot p(x_2)\cdots p(x_n)$. Cela lui permet d’établir, par le même calcul déjà fait pour $\underline{x}$ tout seul, que le code émis $\underline{x}$ est « conjointement typique » avec $\underline{y}$ au sens où il vérifie $$p(\underline{x},\underline{y})\approx 2^{−nH(X,Y)}.$$Il est néanmoins possible qu’un autre code $\underline{x}'$ que celui réellement émis vérifie aussi cette condition. Comme les codes sont choisis indépendamment au hasard, la distribution conjointe pour cet autre code n’est plus $p(\underline x', \underline y)$, mais $q(\underline x', \underline y) = p(\underline x')p(\underline y)$. D’après un calcul similaire à celui déjà fait pour $\underline x$, la probabilité que cela arrive ne dépasse pas $$2^{−nD(p,q)} =2^{−nI(X;Y)}.$$

Le deuxième théorème de Shannon

La notion d’information mutuelle et la borne $2^{−nI(X;Y)}$ ci-dessus permet à Shannon de résoudre le problème théorique de la transmission dans un canal bruité (voir le paradigme de la figure 1). Il s’agit cette fois de maximiser le débit d’information transmis tout en garantissant une communication arbitrairement fiable du message au destinataire.

Pour cela, il suffit de décoder l’information de sorte à récupérer un code $\underline x$ conjointement typique de $\underline y$ en sortie du canal, car la probabilité de tomber sur un $(\underline x, \underline y)$ non typique est arbitrairement faible. La probabilité d’erreur de décodage est donc essentiellement due à la présence éventuelle d’un autre code conjointement typique de $\underline y$, qui donne lieu à une ambiguïté de décodage. D’après ce qu’on vient de voir, la probabilité totale d’erreur due à une telle ambiguïté est bornée par $$N\cdot 2^{−nI(X;Y )}$$où $N$ est le nombre total de codes utilisés dans la transmission.

Pour que cette expression tende vers $0$ quand $n$ tend vers l’infini, il suffit que le débit $(\log_2 N )/n$ soit inférieur à $I(X;Y )$ bits par symbole. Afin de maximiser ce débit, Shannon choisit la distribution de probabilité des codes de sorte que $I (X ; Y )$ soit maximal et nomme $$C =\max_{p(x)} I(X;Y)$$la capacité du canal. Comme la probabilité d’erreur a été calculée en moyenne sur tous les codes possibles, il existe nécessairement au moins une solution pour laquelle il n’y a pas plus d’erreurs. On obtient ainsi le deuxième théorème de Shannon (pour le codage de canal) qui affirme qu’on peut transmettre l’information de façon fiable tant que le débit ne dépasse pas la capacité $C$ du canal.

La formule de Shannon

Le bruit présent dans un canal de transmission est souvent modélisé par du bruit blanc gaussien qui s’ajoute au signal à la réception. Shannon trouve l’expression exacte et étonnamment simple de la capacité de ce canal : $$C =W \cdot \log_2 \bigl(1+ \frac PN\bigr) \text{ bit/s}$$où $W$ est la largeur de bande (en Hertz) et $P/N$ le rapport signal à bruit présent dans la transmission, $P$ désignant la puissance du signal et $N$ la puissance du bruit (Noise). C’est certainement la formule la plus connue de Shannon, celle qui conclue son œuvre. Il popularise à cette occasion le théorème d’échantillonnage démontré auparavant par Edmund Whittaker et Harry Nyquist, qui est souvent (à tort) également appelé théorème de Shannon.

Cette formule fournit un aspect concret de la théorie de l’information qui a séduit de nombreux ingénieurs dès sa parution. Elle est venue juste au bon moment : pas moins de 7 autres chercheurs1 ont publié une formule similaire la même année 1948 !

Shannon... et après ?

L’héritage de Shannon en a dérouté plus d’un : ses théorèmes prévoient qu’il existe de bons systèmes de codage pratiques, mais ne disent pas comment les construire. Paradoxalement, l’idée du codage aléatoire suggère que des codes choisis au hasard forment des solutions quasi-optimales. Sauf qu’avec une dimension tendant vers l’infini, une telle méthode basée sur le hasard est irréaliste en pratique2. Il a fallu 50 ans pour que Claude Berrou, aidé par Alain Glavieux, propose des solutions pratiques (les turbo-codes) qui « imitent » le codage aléatoire et permettent ainsi de s’approcher de très près de la capacité du canal.

Tout ceci n’est qu’un aperçu : la théorie de l’information n’a jamais été aussi vivante et trouve de nombreuses applications en réseaux sans fil, en sécurité de systèmes embarqués, en gestion de portefeuilles, en séquençage génomique, et même en interactions homme-machine.