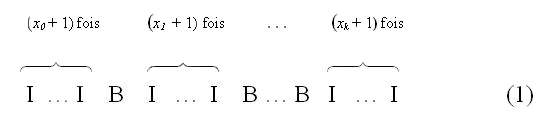Les fonctions (partielles) calculables sont, d’un point de vue informel, des fonctions définies sur une partie de $\mathbb N^k$ ($k\in\mathbb N$), et dont les valeurs (dans $\mathbb N$) peuvent être déterminées par un algorithme (ou une procédure effective), c’est-à-dire un ensemble fini d’instructions, dont l’application n’exige aucune inventivité, et qui permettent d’obtenir la valeur cherchée (lorsqu’elle existe) en un nombre fini d’étapes. Plusieurs classes de fonctions, qui se sont avérées identiques, ont été formellement définies de manière à être calculables en ce sens « intuitif » : les fonctions λ-calculables, récursives, Turing-calculables, etc. Elles fournissent ainsi les meilleurs candidats pour donner une définition formelle de la calculabilité. L’affirmation selon laquelle toute fonction calculable appartient à cette classe est appelée la thèse de Church. Celle-ci ne peut évidemment être démontrée, dans la mesure où elle renferme une notion informelle : il faudrait disposer d'une définition précise de l'expression « fonction calculable » ; or la thèse de Church vise justement à fournir cette définition précise.

C'est le logicien Alonzo Church qui, peu avant Turing, en 1936, énonça une première version de la thèse qui porte désormais son nom. Il identifiait alors les fonctions calculables aux fonctions λ-calculables, celles qui peuvent être définies par un terme du λ-calcul, dont il est l'inventeur. Mais bien que (légèrement) postérieure, la version de Turing, s'est rapidement imposée. Elle consiste à définir la classe des fonctions calculables comme la classe des fonctions dont les valeurs peuvent être calculées par une « machine de Turing ». C'est cette affirmation, équivalente à la thèse de Church proprement dite, que l'on peut appeler la thèse de Church-Turing.

Pour expliciter cette dernière, il nous suffit donc de définir les fonctions Turing-calculables (T-calculables), c’est-à-dire calculables par une machine de Turing. Il existe plusieurs manières de définir une telle machine (abstraite). N’ayant pas besoin, dans un premier temps, d’une définition plus générale, nous pouvons nous donner un alphabet constitué d’une infinité (dénombrable) de symboles d’états internes qi ainsi que des symboles B, I (les symboles d’entrée) et R, L (symboles de déplacement). Un quadruplet est une expression de l’une des formes suivantes :

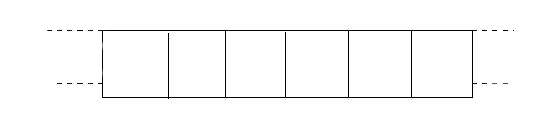
où les S_i désignent des symboles d’entrée. Pour comprendre la signification d’un quadruplet, il faut concevoir la machine comme étant constituée d’un ruban infini divisé en une infinité de cases (Figure 1).

À chaque instant, une seule de ces cases est « observée », ou « lue », par la machine, et celle-ci peut y inscrire un I ou un B (ce qui revient à effacer le contenu de la case, car B fait ici office « d'espace »). Chaque quadruplet correspond, en fait, à une instruction, et la machine n’est rien d’autre qu’un ensemble de telles instructions. Au cours d’un calcul, elle peut être dans divers états. Une instruction du type (a) signifie que si la machine se trouve dans l’état qi en observant Sj, elle doit remplacer ce symbole par Sk et entrer dans l’état ql. L’instruction (b) commande à la machine de se déplacer d’une case à droite (« Right ») et d’entrer dans l’état ql lorsqu’elle est dans l’état qi en observant le symbole Sj. La commande (c) énonce l’instruction correspondante à gauche. Les seules actions élémentaires d’une machine de Turing ainsi définie consistent à écrire, ou à effacer, un symbole I dans une case du ruban, ou à se déplacer d’une case à gauche, ou à droite. De plus, on voit que, pour éviter qu’il y ait à choisir entre deux instructions possibles, une machine ne peut être n’importe quel ensemble de quadruplets : elle ne peut contenir deux quadruplets ayant les mêmes deux premiers symboles. C’est du moins le cas des machines dites déterministes ; mais il peut être utile d’introduire des algorithmes non déterministes.

Il nous faut maintenant préciser comment sont représentés les entiers pour la machine. On considérera que I représente zéro, et une suite de n + 1 symboles I consécutifs désignera le nombre n. Les arguments $x_0,\dots , x_k$ d’une fonction définie sur une partie de $\mathbb N^k$ seront représentés sur le ruban par l’expression :

Évidemment, toutes les autres cases sont vides, c'est-à-dire occupées par un B. On conviendra qu’au début d’une exécution la machine est dans l’état q0 et observe le symbole I le plus à gauche. On considère qu’elle a donné une réponse (i.e., calculé une valeur) si elle s’arrête après un nombre fini d’étapes (aucune nouvelle instruction n’étant applicable) avec une suite finie ininterrompue de symboles I sur le ruban, la machine observant le plus à gauche d’entre eux. La notion d’exécution d’une machine de Turing peut être définie formellement avec précision, ce que nous ne ferons pas ici. Il nous suffira de dire qu’une exécution est une suite de descriptions du contenu du ruban, ou plutôt une description de ce contenu précisant également l’état dans lequel se trouve la machine, ainsi que le symbole observé (ce qui peut être donné en indiquant cet état devant le symbole observé) : l’exécution de M, lorsque celle-ci est appliquée à des arguments inscrits sur le ruban, sera la suite des descriptions du contenu du ruban après chaque application d’une instruction. Un calcul est une exécution finie. Ainsi, avec les conventions qui ont été données, on peut associer à chaque machine M, et chaque entier positif k, une fonction fMk qui pour (m0,..., mk) prend la valeur n si l’exécution de M à (1) s’arrête dans les conditions décrites, et n’est pas définie sinon.

Pour illustrer de façon simple la manière dont fonctionne une machine de Turing, on peut donner l’exemple d’une machine calculant la somme de deux entiers. Pour illustrer de façon simple la manière dont fonctionne une machine de Turing, on peut donner l’exemple d’une machine calculant la somme de deux entiers. On se convaincra aisément que c’est le cas de :

M = { q0IRq0, q0BIq1, q1ILq1, q1BRq2, q2IBq3, q3BRq3, q3IBq4, q4BRq4 }

En effet, le ruban portera initialement deux suites de I séparées par un B et la machine, dans l’état q0, observant le plus à gauche des I, se déplacera vers la droite dans ce même état jusqu’à ce qu’elle rencontre le B séparant les deux suites. Elle le remplacera par I, entrera dans l’état q1 dans lequel elle poursuivra en se déplaçant vers la gauche jusqu’à ce qu’elle rencontre un B à partir duquel, entrant dans l’état q2, elle se déplacera d’une case à droite, et supprimera un I puis, dans l’état q3 effacera un autre I et enfin, dans l’état q4, se placera sur le premier I à gauche. Au total, la machine a effacé deux I après en avoir ajouté un (de manière à obtenir une suite ininterrompue), ce qui fournit effectivement le résultat cherché.

On peut voir la thèse de Church-Turing comme visant non seulement à définir la classe des fonctions calculables, mais aussi la notion même de procédure effective (ou algorithmes). Mais les choses sont un peu moins simples ici. Car lorsque l'on montre, par exemple, que la classe des fonctions T-calculables est exactement celle des fonctions λ-définissables, ou celle des fonctions récursives, ou celle des fonctions calculables par les algorithmes de Markov, on peut encore s'interroger sur ce que ces résultats nous enseignent sur la notion même d'algorithme ; celle-ci est-elle davantage « capturée » par les machines de Turing, les règles du λ-calcul, les opérations définissant les fonctions récursives, les « prescriptions » de Markov, etc. ?

On voit qu'il y a donc deux manières d'interpréter la thèse. La première (définition d'une classe de fonctions) est corroborée chaque fois que l'on démontre l'identité de deux classes définies indépendamment ; la seconde ne peut être justifiée que par une analyse de la notion informelle d'algorithme de calcul — ce qu'avait précisément entrepris Turing dans l'article fondateur de 36.