Le changement de variable fait partie de toute la panoplie de techniques inventées pour calculer la valeur d'une intégrale : intégration par parties, théorèmes d'interversion d'intégrales, théorème des résidus en analyse complexe,... Nous nous proposons de l'analyser en une dimension puis en dimension quelconque. Outre le bagage théorique nécessaire pour étayer cette technique, l'objectif principal est de donner une interprétation du résultat, afin d'appliquer plus naturellement la formule. En effet, cette dernière n'est pas agréable à manipuler, et nécessite un peu d'entraînement pour s'y familiariser. Bien qu'elle soit facile à redémontrer en une dimension, son importance et sa fréquence d'utilisation sont telles que quelques astuces pour la retrouver rapidement sont bienvenues.

De plus, bien connaître le principe avec une seule variable permet de passer sereinement à sa généralisation au cas des intégrales multiples. C'est l'objet de la dernière partie, à l'origine assez succincte et qui a finalement pris une ampleur conséquente.

Attention : mise à part la deuxième section ("La théorie") et la dernière sous-section, tout est volontairement heuristique et non-rigoureux, afin de mieux mettre en lumière la philosophie qui sous-tend cette formule et s'écarter de la grande majorité des documents qui traitent le sujet de façon très chirurgicale.

J'en profite pour remercier tous les doctorants et toutes les doctorantes qui m'ont relu et qui ont relevé de nombreuses corrections à faire, améliorant sensiblement le résultat.
 

La pratique

Pour $f$ et $\varphi$ vérifiant les bonnes hypothèses et définies aux bons endroits, pour $a, b \in \mathbb{R}$, on a la formule
$$\int_{\varphi(a)}^{\varphi(b)} f(x)dx = \int_a^b f \circ \varphi(t)\varphi'(t)dt.$$

On a donc opéré le changement de variable $x = \varphi(t)$. Pour passer d'une intégrale à l'autre, on a changé, outre la variable bien sûr :

•     le pas d'intégration (apparition de "$\varphi'(t)$");
•     les bornes de l'intégrale.

Le pas d'intégration

Pourquoi ce $\varphi'(t)$ apparaît-il dans la formule du changement de variable ? Quelle interprétation peut-on lui donner ? Rien ne vaut un retour aux sources pour comprendre son origine. La mise en situation qui suit est inspirée de 1, page 18.

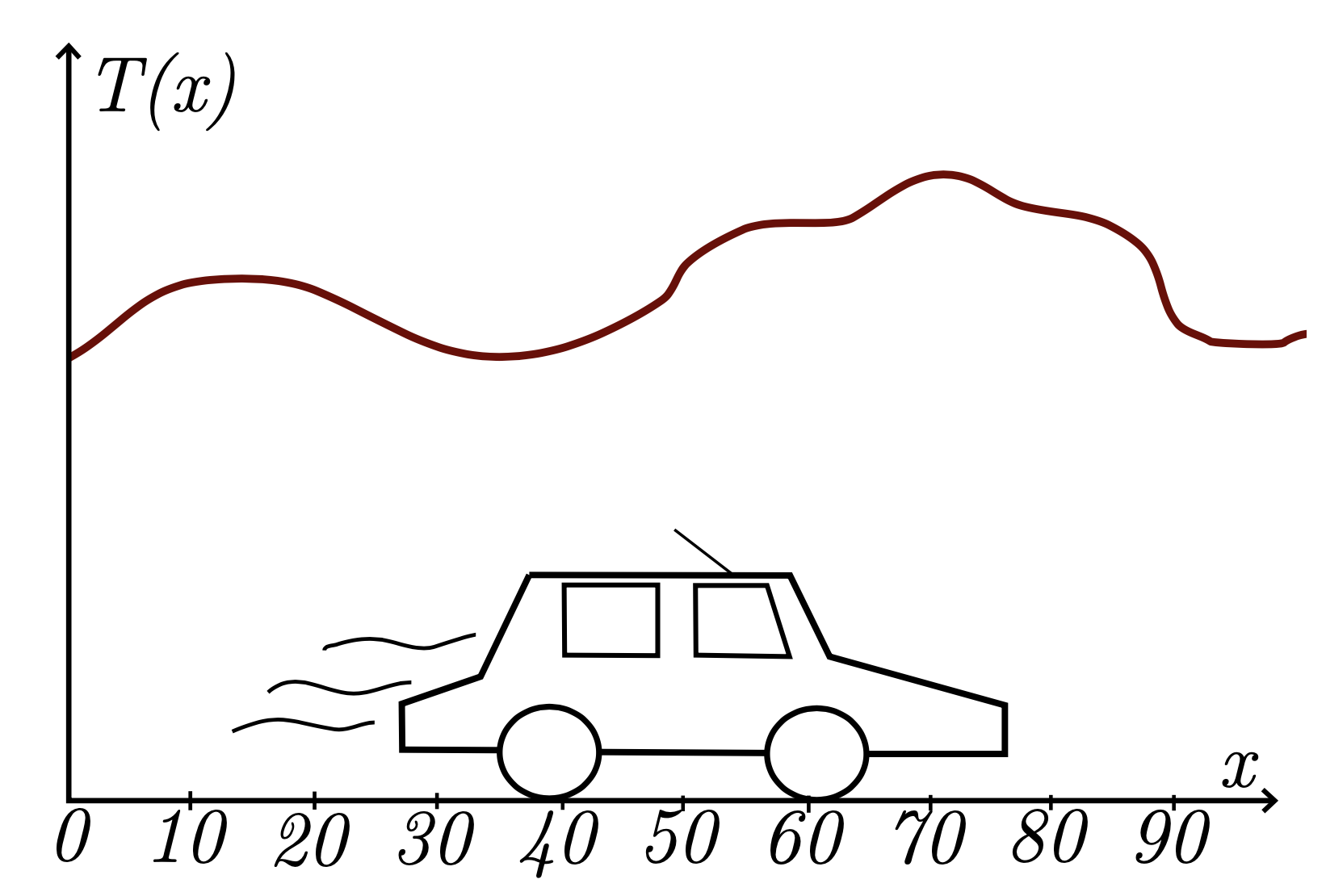
Supposons que vous parcourez régulièrement en voiture une route de cent kilomètres, et qu'un beau matin, vous vous demandez : "Mais au fait, quelle est la température moyenne le long de cette route ?". Vous prenez avec vous votre appareil favori pour mesurer la température, et c'est parti pour un super trajet.

Quelle formule vous permet de calculer cette moyenne, que l'on va noter $M$ ? Si on visualise la température comme une fonction continue sur l'espace (ici la route, un segment donc), alors $M$ correspond à l'aire sous sa courbe divisée par la longueur de l'intervalle choisi (ici, $100$ km); autrement dit,

$$M = \frac{1}{100} \int_0^{100} T(x)dx,$$

où $T$ est votre appareil de mesure, i.e. la fonction qui à l'endroit $x$ sur la route renvoie la température mesurée.

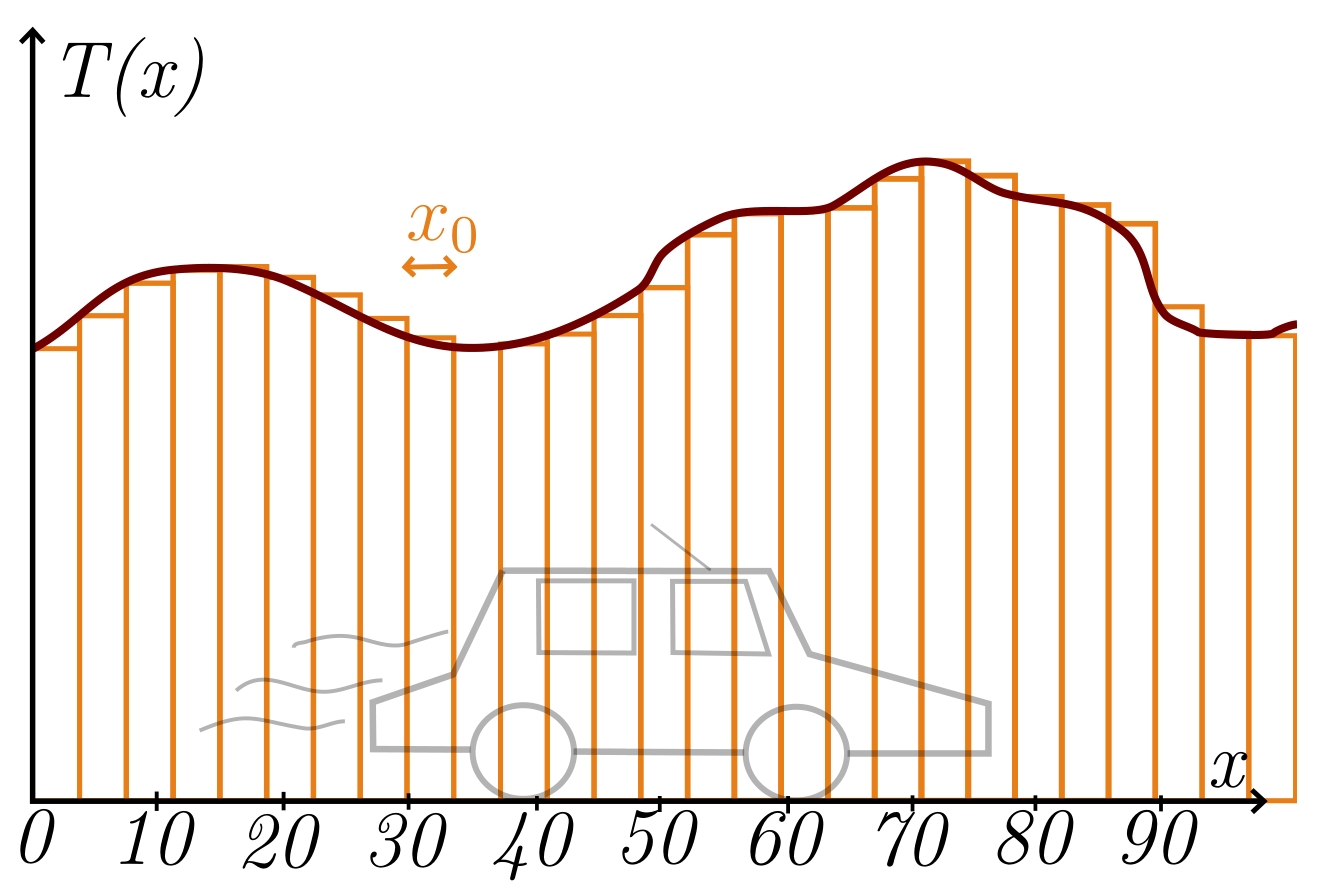
Concrètement, vous ne pouvez prendre qu'un nombre fini de mesures, donc vous ne connaîtrez la température qu'en un nombre fini de points. Il vous faudra dès lors approcher cette intégrale en faisant une moyenne discrète, en prenant par exemple une mesure tous les cent mètres, ou bien plus fréquemment encore si vous voulez une meilleure approximation. C'est essentiellement comme ça que vous avez défini l'intégrale de Riemann d'une fonction continue :

c'est la limite que vous obtenez quand vous faites tendre votre pas vers $0$, ou de façon équivalente quand vous faites tendre le nombre de subdivisions de votre intervalle d'intérêt vers l'infini. Avec une formule, on a, pour tous $a < b \in \mathbb{R}$ et pour toute fonction $f$ continue sur $[a,b]$ :

 

 

$$\int_{a}^{b} f(x) dx := \lim\limits_{N_0 \rightarrow +\infty} \sum_{n = 0}^{N_0} \frac{b-a}{N_0}f\left(n\frac{b-a}{N_0}\right),$$
où la fraction $\frac{b-a}{N_0}$ correspond au pas $x_0$.

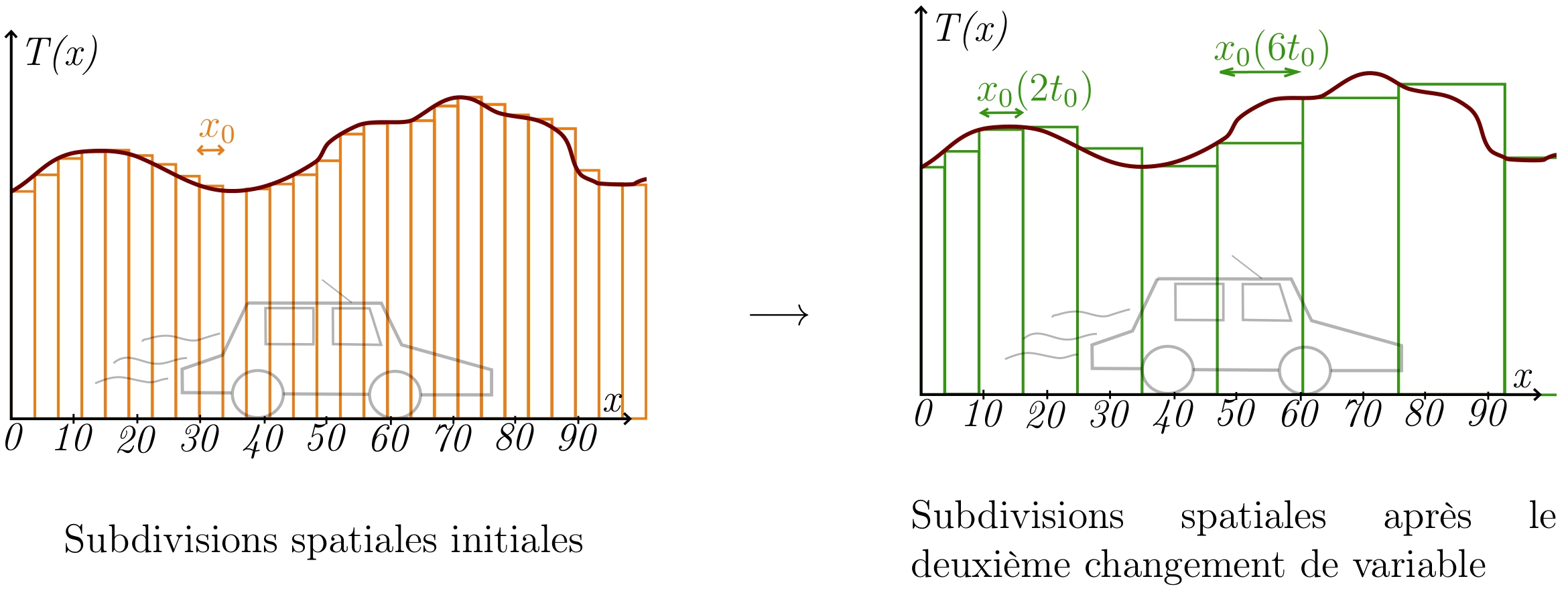
Mais s'il vous faut vous arrêter tous les cent mètres, en plus d'être très pénible, cela vous demandera une précision extrême pour ne pas faire d'erreur. Or vous savez que la distance parcourue $x$ est reliée à la vitesse et au temps par la formule $v = \frac{x}{t}$, et vous avez justement un régulateur de vitesse sur votre belle voiture neuve. Vous pouvez donc choisir une vitesse constante $v_0$, et paramétrer votre appareil de mesure pour qu'il prenne une mesure toutes les vingt secondes par exemple.

Par conséquent, il vous faut effectuer un changement de variable dans votre intégrale, de l'espace $x$ vers le temps $t$. Mais restons pour le moment dans le monde discret. Si vous choisissez un pas en espace $x_0 = \frac{100}{N_0}$ où $N_0$ est le nombre correspondant de découpages de notre route en segments de même longueur, la somme qui vous intéresse est donc $\frac{1}{100}\sum_{n = 0}^{N_0} x_0 T(nx_0)$. Quand $x_0$ tend vers $0$, cette somme tend vers $\frac{1}{100}\int_0^{100} T(x)dx$. Si vous roulez à vitesse constante $v_0$, on a $x = v_0t ~ (=\varphi(t))$, donc on peut prendre le pas de temps correspondant $t_0 = \frac{x_0}{v_0}$. Puisque $N_0 = \frac{100}{x_0}$, on obtient :
$$\sum_{n = 0}^{N_0} x_0 T(nx_0) = \sum_{n = 0}^{100/v_0t_0} v_0t_0 T(nv_0t_0) \underset{t_0 \to 0}{\longrightarrow} \int_{0}^{100/v_0} v_0 T(tv_0)dt.$$

On voit le paramètre $v_0 = \varphi'(t)$ qui fait son apparition. Remarquez aussi le changement de bornes par rapport à l'intégrale de départ !

Compliquons l'exemple : votre voiture n'est pas si neuve que cela, et votre régulateur de vitesse débloque : il vous donne constamment une très légère accélération notée $a$, de sorte que votre vitesse devienne non plus constante mais affine, donnée en fonction du temps par $v(t) = v_0 + at$. Dans ce cas, $x(t) = v_0t + \frac{a}{2}t^2$; en particulier, un pas de temps constant $t_0$ n'implique plus un pas d'espace constant (car $x(t+t_0)-x(t) = v_0t_0 + \frac{a}{2}(2tt_0+t_0^2)$). Il vous faut donc réadapter votre méthode, sachant que vous ne pouvez programmer qu'une fréquence constante pour la prise de mesures. Par conséquent, l'essentiel de vos mesures sera concentré au début, donc vous aurez besoin de pondérer lesdites mesures. C'est le rôle du $\varphi'(t)$ dans la formule.

Voyons ce que cela donne : si on garde un pas de temps $t_0$ constant, comment varie le pas en espace $x_0(t)$ en fonction du temps ? Étant donné $n \in \mathbb{N}$, la distance entre deux mesures successives est donnée par \begin{align*} x_0(nt_0) = x((n+1)t_0) - x(nt_0) & = v_0t_0 + ((n+1)^2 - n^2)\frac{a}{2}t_0^2 \\ & = v_0t_0 + (2n+1)\frac{a}{2}t_0^2.\end{align*}
Soit $N$ positif tel que $x(Nt_0) = 100$; une résolution d'équation du deuxième degré montre que $N = 2\frac{-v_0 + \sqrt{v_0^2 + 200a}}{at_0}$. Notons $C := t_0N = 2\frac{-v_0 + \sqrt{v_0^2 + 200a}}{a}$. On peut maintenant calculer :
\begin{align*}
& \sum_{n = 0}^{N} x_0(nt_0) T(x(nt_0)) = \sum_{n = 0}^{N} \left(v_0t_0 + (2n+1)\frac{a}{2}t_0^2\right) T\circ x (nt_0) \\
& \hspace{1cm}  = v_0\sum_{n = 0}^{N} t_0T\circ x (nt_0) + a\sum_{n = 0}^{N} t_0 \cdot nt_0T\circ x (nt_0) + \frac{a}{2}t_0 \sum_{n = 0}^{N} t_0 T\circ x (nt_0) \\
& \hspace{1cm} \underset{t_0 \to 0}{\longrightarrow} v_0 \int_{0}^C T\circ x(t)dt + a\int_{0}^C t T\circ x(t) dt \\ & \hspace{4cm} = \int_{0}^C (v_0 + at)T\left(v_0t + \frac{a}{2}t^2\right)dt
\end{align*}

Pour conclure, nous avons donc fait les deux changements de variable suivants :

\begin{align*}
    \frac{1}{100} \int_0^{100} T(x)dx & = \frac{1}{100}\int_{0}^{100/v_0} v_0 T(tv_0)dt \\ \text{et} \hspace{.5cm} \frac{1}{100} \int_0^{100} T(x)dx & = \frac{1}{100} \int_{0}^{2\frac{-v_0 + \sqrt{v_0^2 + 200a}}{a}} (v_0 + at) T\left(v_0t + \frac{a}{2}t^2\right)dt.
\end{align*}
Le premier correspond à $x = tv_0$, le second à $x = tv_0 + \frac{a}{2}t^2$. Dans le premier cas, le pas d'intégration a subi une dilatation d'un facteur $v_0$ (dérivée de $t \mapsto tv_0$), dans le deuxième cas, on le multiplie par la dérivée de $t \mapsto tv_0 + \frac{a}{2}t^2$.

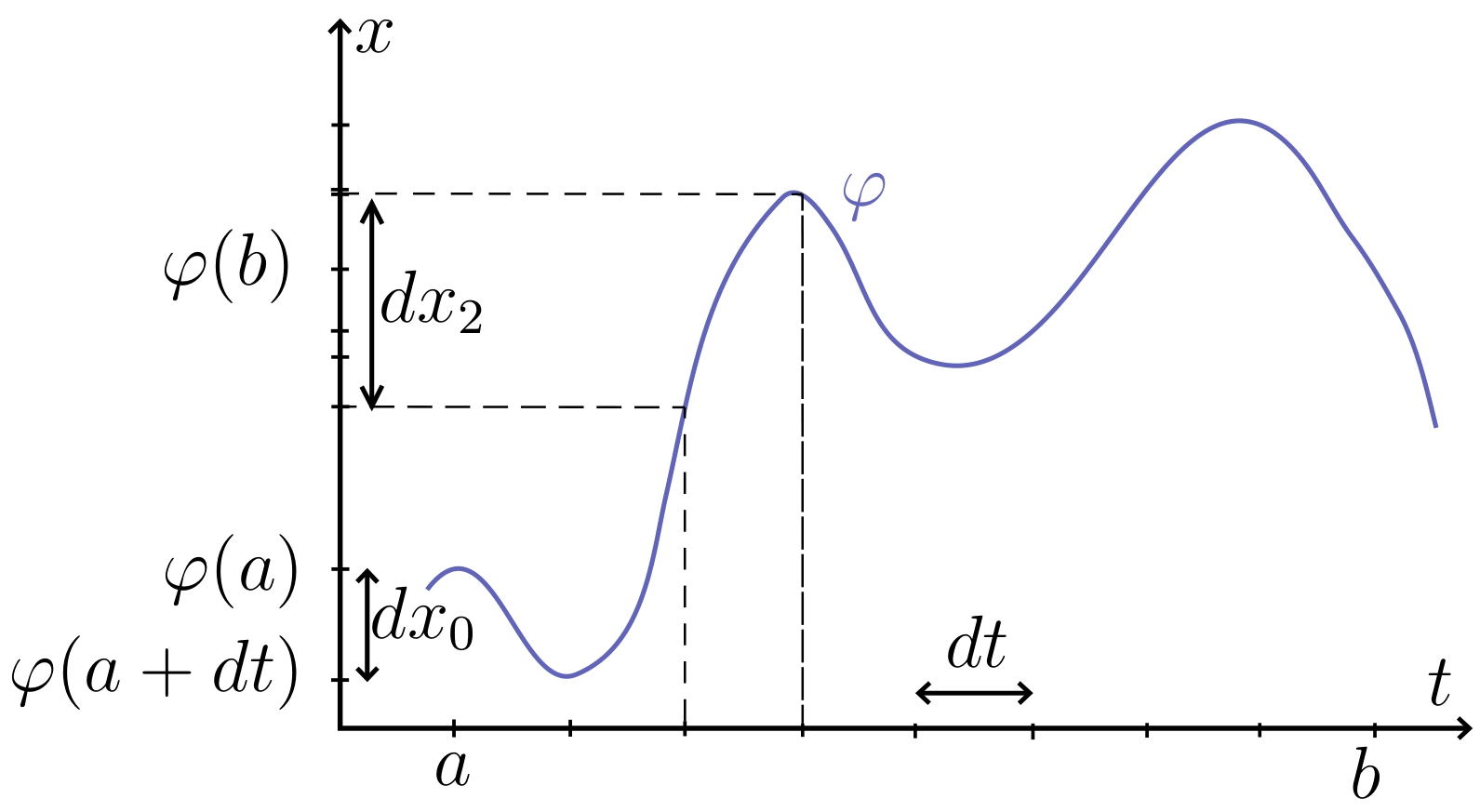
Pourquoi est-ce précisément la dérivée qui intervient ? Prenons deux réels $a < b$, une fonction $f$ et une fonction $\varphi$ tels que le théorème du changement de variable s'applique.

Si on considère un très petit pas $dt$, avec lequel on veut approcher l'aire sous la courbe entre $a$ et $b$ de la composée $f \circ \varphi$, on doit faire une moyenne des valeurs de $f \circ \varphi$ en $a$, $a + dt$, $a + 2dt$, ..., $b-dt$, $b$. Cela correspond à regarder les valeurs de $f$ en $\varphi(a)$, $\varphi(a+dt)$, $\varphi(a+2dt)$, ..., $\varphi(b-dt)$, $\varphi(b)$. Le $n^{\text{ème}}$ pas $dx_n$ est ainsi donné par
\begin{align*}
    dx_n & = \varphi(a + (n+1)dt) - \varphi(a + ndt) \\ & = dt \frac{\varphi(a + (n+1)dt) - \varphi(a + ndt)}{dt} \\ & \approx \varphi'(a + ndt)dt.
\end{align*}

Finalement, ce sont les variations infinitésimales de $\varphi$ qui modifient le pas (notion infinitésimale par nature), d'où l'apparition de sa dérivée.

Concrètement. Une astuce très pratique pour ne pas trop se poser de question sur la place et le calcul de $\varphi'(t)$ est d'écrire $x = \varphi(t)$, et d'utiliser les notations physiques : comme $x$ dépend de $t$, on peut dériver l'équation précédente par rapport au temps pour obtenir $\frac{dx}{dt} = \varphi'(t)$, puis "multiplier" des deux côtés par $dt$ (cela n'a pas de sens mathématique, mais c'est bien pratique) pour trouver $$dx = \varphi'(t)dt.$$

Notez que cette dernière équation peut être rendue rigoureuse grâce à la théorie des formes différentielles, qui est fondamentale en géométrie différentielle. Elle permet notamment de donner une définition précise aux objets du type $dx$, conférant un sens plus mathématique à l'apparition de ce dernier dans l'écriture $\int_{a}^{b}f(x)dx$ (autre que juste se souvenir par rapport à quelle variable on intègre, comme on l'apprend en classe de terminale !). Elle est de plus un cadre optimisé pour la notion d'orientation, et beaucoup de concepts s'y traitent de façon plus fluide. Mais en parler plus en détails augmenterait considérablement la longueur de ce document !

Les bornes

Partons de l'intégrale $\int_{\alpha}^{\beta} f(x)dx$, où $\alpha$ et $\beta$ sont des réels. Supposons qu'on arrive à exprimer $x$ sous la forme $\varphi(t)$ pour une fonction $\varphi$ "pas trop méchante". Dans l'intégrale de départ, $x = \varphi(t)$ varie de $\alpha$ à $\beta$.

Si $\varphi$ est bijective, on trouve que $t$ varie de $a := \varphi^{-1}(\alpha)$ à $b := \varphi^{-1}(\beta)$ (remarquons que si $\varphi^{-1}(\alpha) > \varphi^{-1}(\beta)$, cela change le sens de parcours de l'intégrale !). On a donc $$\int_{\alpha}^{\beta} f(x)dx = \int_{\varphi(a)}^{\varphi(b)} f(x)dx = \int_a^b f \circ \varphi(t)\varphi'(t)dt.$$

Que se passe-t-il si $\varphi$ n'est pas bijective ? En regardant de plus près la démonstration du théorème (cf. section "La théorie"), le fait qu'il y ait plusieurs choix d'antécédents possibles n'altère pas les arguments à l'œuvre. Donc il suffit de trouver un antécédent par $\varphi$ de $\alpha$ et de $\beta$, peu importe lesquels, à ceci près qu'il faut les choisir de façon à ne pas sortir des ensembles de définition de nos fonctions (exemple 3) ! Attention aussi à ne pas compliquer inutilement les calculs en prenant des antécédents exotiques qui entraînent facilement des erreurs (exemple 2).

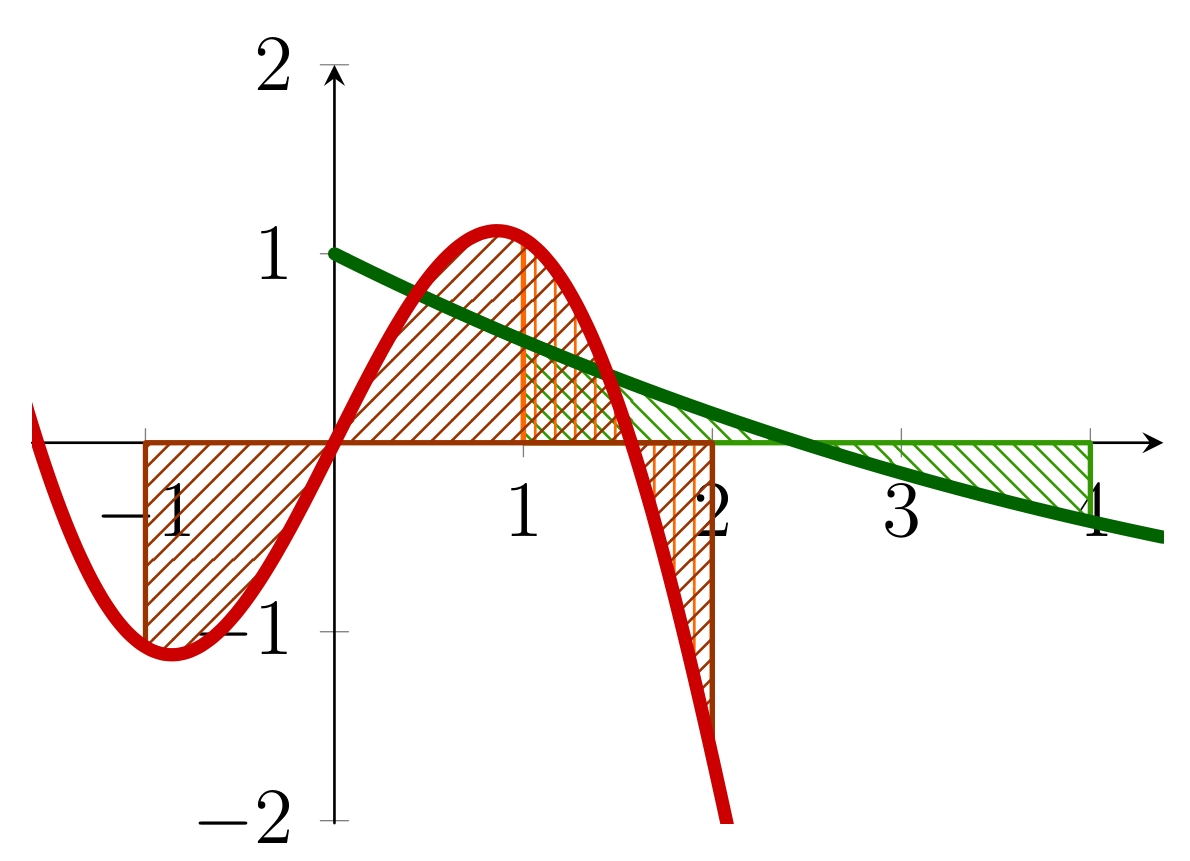
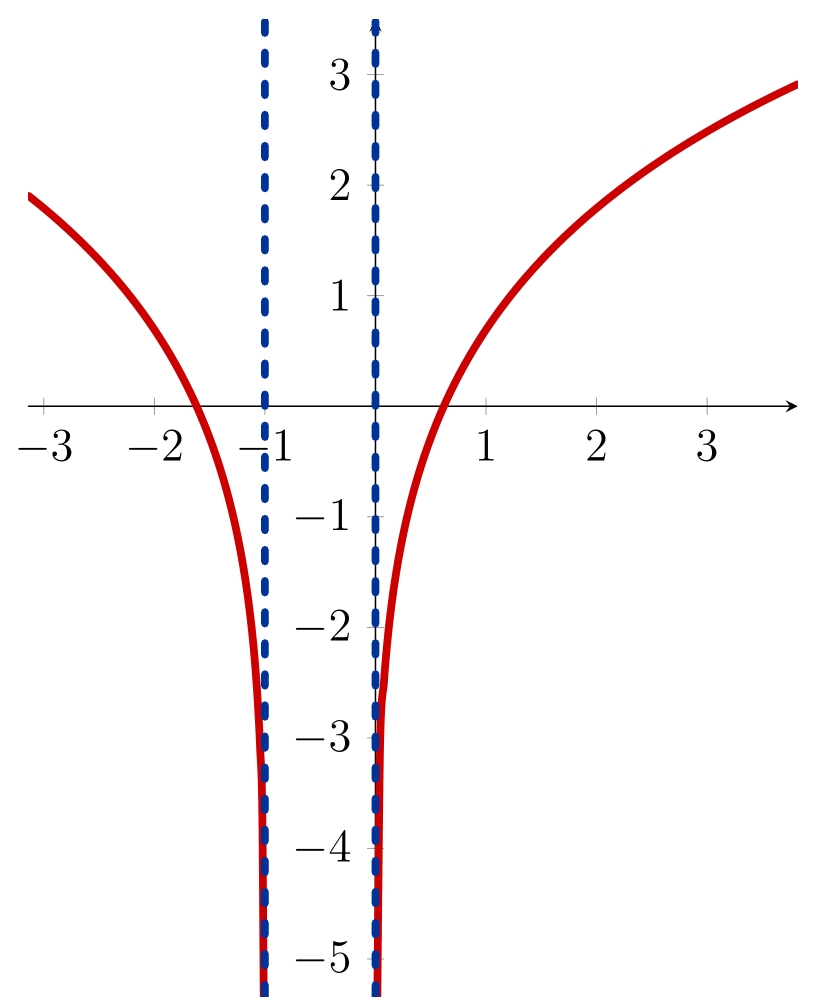
Exemple 1. Calculons $\int_{1}^{4} \cos(\sqrt{x})dx$. En effectuant le changement de variable $x = \varphi(t) = t^2$, le pas d'intégration $dx$ devient $\varphi'(t)dt = 2tdt$. On obtient ainsi
$$\int_{1}^{4} \cos(\sqrt{x})dx = \int_a^b 2t \cos(t) dt,$$ où $a$ et $b$ sont des antécédents par la fonction carré de $1$ et de $4$ respectivement, donc déterminés au signe près. En effectuant une intégration par parties, on arrive ensuite à
$$\int_{1}^{4} \cos(\sqrt{x})dx = 2 \bigg(\big[t\sin(t)\big]_a^b - \int_a^b \sin(t)dt \bigg) = 2 \big(\big[t\sin(t)\big]_a^b + \big[\cos(t)\big]_a^b \big).$$

Ici, on voit que la parité des fonctions $t \mapsto t\sin(t)$ et $t \mapsto \cos(t)$ annule l'effet du choix des signes de $a$ et de $b$. Le graphique ci-contre l'illustre : en vert la fonction $x \mapsto \cos(\sqrt{x})$, en rouge la fonction $x \mapsto 2x\cos(x)$. Les trois aires hachurées, comptées avec le signe, sont égales.

Exemple 2. Calculons $\int_{\frac{\pi^2}{4}}^{\pi^2} \frac{\cos(\sqrt{x})}{\sqrt{x}}dx$. On effectue le changement de variable $x = \varphi(t) = t^2$ comme précédemment, et on est tenté d'écrire que $\int_{\frac{\pi^2}{4}}^{\pi^2} \frac{\cos(\sqrt{x})}{\sqrt{x}}dx$ se transforme en $\int_{-\frac{\pi}{2}}^{-\pi} \frac{\cos(t)}{t}2tdt = \int_{-\frac{\pi}{2}}^{-\pi} 2\cos(t)dt$ par exemple. Mais pourtant, $$\int_{-\frac{\pi}{2}}^{-\pi} 2\cos(t)dt = 2\big[\sin(t)\big]_{-\frac{\pi}{2}}^{-\pi} = -2\sin(\pi) + 2\sin\left(\frac{\pi}{2}\right) = 2,$$ tandis que $$\int_{\frac{\pi}{2}}^{\pi} 2\cos(t)dt = 2\sin(\pi) - 2\sin\left(\frac{\pi}{2}\right) = -2\ldots$$ En réalité, en choisissant des antécédents négatifs sans prendre un minimum de précautions, on introduit une erreur de signe (bravo si vous l'aviez repérée avant d'arriver au bout des calculs !). En effet, il ne faut pas oublier que $\sqrt{t^2} = \vert t \vert$, donc le bon changement de variable ici est $$\int_{\frac{\pi^2}{4}}^{\pi^2} \frac{\cos(\sqrt{x})}{\sqrt{x}}dx = \int_{-\frac{\pi}{2}}^{-\pi} \frac{\cos(\vert t \vert)}{\vert t \vert}2tdt.$$ Donc même si on s'en sort dans la théorie, choisir des antécédents exotiques n'apporte rien si ce n'est plus de chances de faire des erreurs de calcul.

Exemple 3. On s'intéresse maintenant à $\int_6^{12} \ln(x) dx$. Le changement de variable $x = t^2 + t = \varphi(t)$ (complètement inutile pour calculer l'intégrale demandée ici) donne un pas d'intégration du type $(2t + 1)dt$. L'équation $t^2 + t = 6$ a deux solution, $-3$ et $2$, tandis que $3$ et $-4$ sont les deux solutions de $t^2 + t = 12$. Ainsi, on est tenté d'écrire
\begin{align*} \int_6^{12} \ln(x) dx & = \int_2^3 \ln(t^2 + t)(2t+1)dt \\ & = \int_{-3}^3 \ln(t^2 + t)(2t+1)dt,\end{align*} mais la dernière intégrale n'est pas définie car sur $]-1;0[$, la fonction $t \mapsto t^2 + t$ ne prend que des valeurs strictement négatives, donc son logarithme (représenté en rouge ci-dessus) n'est pas défini...

Une autre erreur possible est de ne pas changer la variable elle-même mais une expression de la variable. Cela revient finalement à parcourir la formule du changement de variable $\int_{\varphi(a)}^{\varphi(b)} f(x)dx = \int_a^b f \circ \varphi(t)\varphi'(t)dt$ de la droite vers la gauche. C'est très risqué ! Par exemple, si on veut calculer $\int_0^{\pi} e^{\sin(t)}dt$, et qu'on veut écrire $\sin(t) (=\varphi(t)) = x$, le changement de pas d'intégration donne $dx = \varphi'(t)dt$, donc $dt = \frac{dx}{\varphi'(t)} = \frac{dx}{\cos(t)}$, qui dépend encore de $t$ (première étape pénible, car il faut maintenant exprimer $\varphi'(t)$ en fonction de $x$...). Mais quelqu'un qui voudrait aller un peu vite dirait alors que $\varphi(0) = \sin(0) = 0$ et $\varphi(\pi) = \sin(\pi) = 0$, voire écrirait $\int_0^{\pi} e^{\sin(t)}dt = \int_0^0 \frac{e^x}{\cos(t)}dx$, donc les bornes de l'intégrale qu'on obtiendrait seraient les mêmes et l'intégrale serait nulle. Ce qui n'est clairement pas le cas puisqu'on intègre une fonction continue strictement positive sur un intervalle de longueur $\pi$. Ici, il faut bien voir qu'en faisant les choses dans le bon ordre, le changement de variable qu'on opère est $t = \arcsin(x)$, or $\arcsin$ n'est définie que sur $[-1;1]$, donc ce changement de variable n'est pas valable ici.

Moralité. Une méthodologie efficace est la suivante :

• parcourir la formule du changement de variable de la gauche vers la droite, i.e. partir de $\int_{\alpha}^{\beta} f(x)dx$ et exprimer $x$ en fonction de $t$.
• commencer par vérifier que l'intervalle $[\alpha, \beta]$ est inclus dans l'image du changement de variable $\varphi$ choisi, ce qui par continuité revient à s'assurer que $\alpha$ et $\beta$ sont dans l'image de $\varphi$.
• pour trouver rapidement les bornes, se poser la question : "si $x$ varie de $\alpha$ à $\beta$, quels $a$ et $b$ puis-je trouver pour que si $t$ varie de $a$ à $b$, alors $x = \varphi(t)$ varie de $\alpha$ à $\beta$ ?".
• attention !! Si l'équation $\varphi(t) = \alpha$ ou l'équation $\varphi(t) = \beta$ possèdent plus d'une solution, il faut s'assurer que les solutions $a$ et $b$ choisies ($\varphi(a) = \alpha$, $\varphi(b) = \beta$) soient telles que l'image de $[a,b]$ par $\varphi$ soit bien incluse dans le domaine de définition de $f$.

C'est le dernier point qui posait problème dans le choix des antécédents de l'exemple 3.
 

La théorie

Prenons tout de même soin de démontrer la formule du changement de variable proprement, et veillons à expliciter les hypothèses de départ. Tout comme le principe de l'intégration par partie est d'intégrer l'expression $(UV)' = U'V + V'U$, une preuve concise consiste à intégrer $(U \circ V)' = V' \cdot U' \circ V$. Un énoncé possible du changement de variable est le suivant :

Théorème. Soit $\varphi \colon [a,b] \longrightarrow I$ une fonction $\mathscr{C}^1$ et $f \colon I \longrightarrow \mathbb{R}$ une fonction continue. Alors $$\int_{\varphi(a)}^{\varphi(b)} f(x)dx = \int_a^b f \circ \varphi(t)\varphi'(t)dt.$$

Démonstration. Notons $F \colon I \longrightarrow \mathbb{R}$ une primitive de $f$, par exemple $F(y) := \int_{\varphi(a)}^y f(x)dx$ pour $y \in I$. Par conséquent, la composée $F \circ \varphi$ est de classe $\mathscr{C}^1$ sur $[a,b]$, et sa dérivée est $(F \circ \varphi)'(t) = \varphi'(t) f\circ \varphi(t)$. En intégrant entre $a$ et $b$, on trouve donc
\begin{align*} \int_a^b f \circ \varphi(t)\varphi'(t)dt & = \int_a^b (F \circ \varphi)'(t)dt = \left[F\circ \varphi(t)\right]_a^b \\ & = \left[F(x)\right]_{\varphi(a)}^{\varphi(b)} = \int_{\varphi(a)}^{\varphi(b)} f(x)dx. \square \end{align*}

Comme nous l'avons vu dans la section Pratique, la formule du changement de variable telle qu'écrite précédemment est parcourue usuellement de gauche à droite; autrement dit, on part de $\int_{\varphi(a)}^{\varphi(b)} f(x)dx$ qu'on veut calculer. Mais l'intégrale qu'on écrit sera plutôt de la forme $\int_{\alpha}^{\beta} f(x)dx$. Le cas où $\varphi$ est de plus bijective mérite qu'on le mentionne, car il permet de réécrire la formule de telle sorte qu'elle devienne facilement applicable :
$$\int_{\alpha}^{\beta} f(x)dx = \int_{\varphi^{-1}(\alpha)}^{\varphi^{-1}(\beta)} f \circ \varphi(t)\varphi'(t)dt$$

Soulignons encore une fois que l'hypothèse à ne surtout pas oublier ici est que $\varphi([a,b])$ soit inclus dans le domaine de définition de $f$, ce qui, si $\varphi$ n'est pas bijective, ne consiste pas forcément à s'assurer que $\varphi(a) \in I$ et $\varphi(b) \in I$... Gardez l'exemple 3 en tête !

Personnellement, je vous recommande d'aiguiser des astuces de calcul comme celles explicitées dans la section précédente plutôt que d'appliquer les formules. Il est extrêmement facile de se tromper dans la formule, et si vous devez l'utiliser telle quelle, prendre le temps de la redémontrer peut s'avérer salvateur et vous faire économiser de nombreuses minutes à vous demander où est l'erreur dans vos calculs.

Vers les dimensions supérieures

L'objectif de cette section n'est pas de tout comprendre des intégrales multiples et du changement de variable en dimension $12$, mais d'analyser les éléments qui entrent en jeu dans la formule en dimension $1$, afin de deviner leurs analogues en dimensions supérieures et d'écarter les éventuelles obstructions à cette généralisation.

L'intégrale de Riemann sur $\mathbb{R}^n$ et la formule du changement de variables

Remarquons qu'en dimension $1$, les ensembles sur lesquels on intègre sont des intervalles, au pire des réunions d'intervalles. Un intervalle est une brique élémentaire sur laquelle s'appuie fortement l'intégration, puisque si on reprend la définition des sommes de Riemann, on approche notre fonction $f$ qu'on veut intégrer par des fonctions constantes par morceaux, où les morceaux sont des intervalles de plus en plus petits. Or l'intégrale d'une fonction constante sur un intervalle est naturellement définie comme la constante en question multipliée par la longueur de l'intervalle.

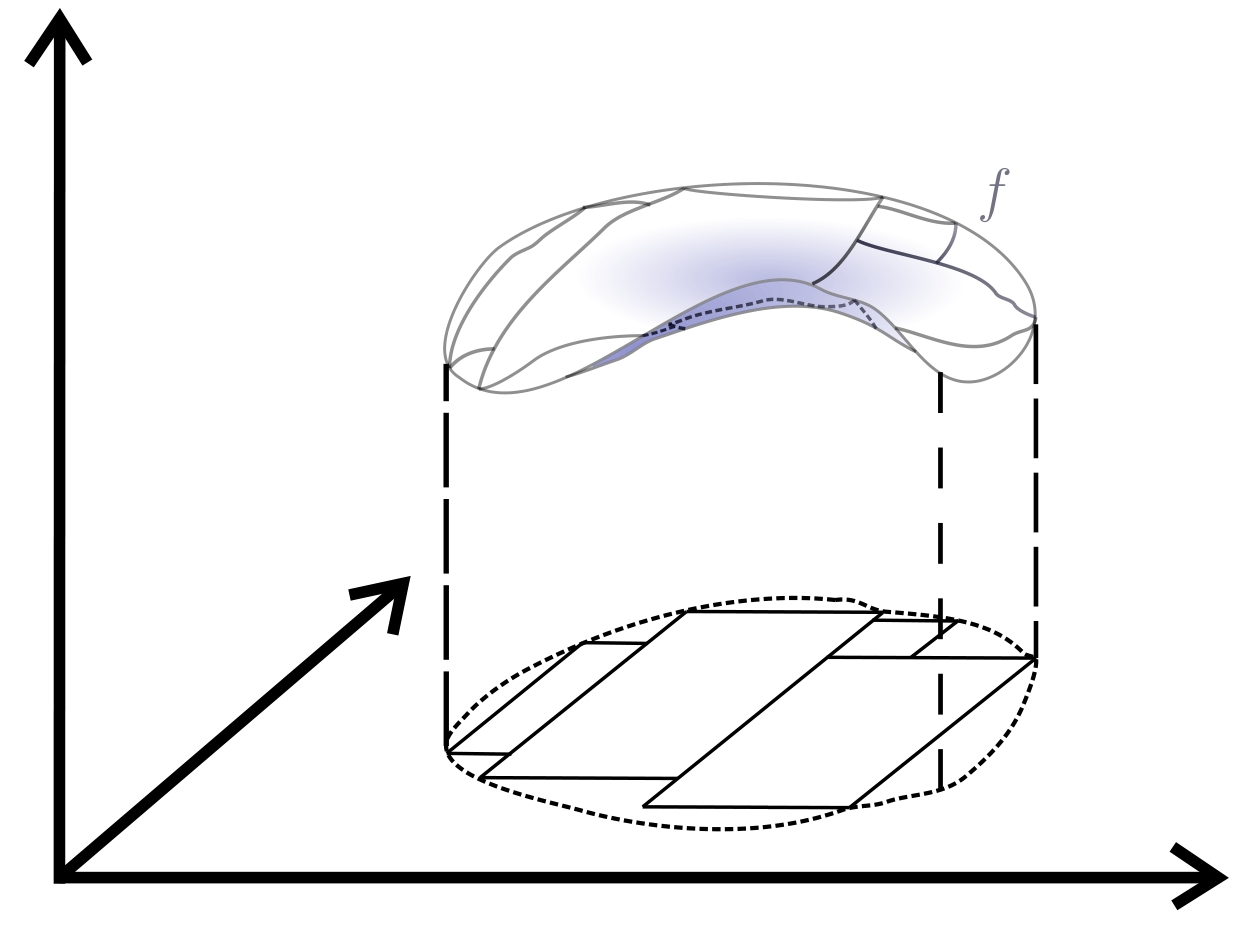
En dimensions supérieures, la notion correspondant aux intervalles est celle des pavés. En dimension $2$ par exemple, il s'agit des rectangles, mais on imagine facilement des ensembles aux bords incurvés assez loin d'être des rectangles ou des réunions finies de rectangles. Ainsi, pour définir l'intégrale d'une fonction $f$ sur un disque, il faudra approcher le disque par une union de rectangles de plus en plus petits, qui vont couvrir in fine tout le disque, et pour chaque rectangle, compter sa superficie multipliée par une constante assez proche des valeurs prises par $f$ sur ce rectangle.

Ce qui complique les choses par rapport au cas unidimensionnel est donc qu'il faut approcher non-seulement la fonction mais aussi l'ensemble de départ ! C'est pourquoi bien souvent on ramène des intégrales multiples à des intégrales unidimensionnelles pour pouvoir les calculer, via les théorèmes de Fubini. Du moins, quand on y arrive !

Ceci étant dit, choisissons un entier $n \geq 1$ et explicitons les termes qui apparaissent dans le changement de variables en dimension $n$. Notons $\textbf{x} := (x_1,\ldots,x_n)$ et $\textbf{t} := (t_1,\ldots,t_n)$ nos variables $n$-dimensionnelles. Si $D \subseteq \mathbb{R}^n$ est un sous-ensemble borné et "ouvert" (pour tout point de $D$, on doit pouvoir trouver une boule contenue dans $D$ et contenant ce point), la formule du changement de variables est donnée par $$\int_{\varphi(D)} f(\textbf{x})d\textbf{x} = \int_D f \circ \varphi(\textbf{t}) \left\lvert\det(\mathrm{Jac}_{\textbf{t}}\varphi)\right\rvert d\textbf{t},$$ où $f$ et $\varphi$ doivent bien sûr vérifier certaines hypothèses. On se doute que $\varphi \colon D \longrightarrow \varphi(D) \subseteq \mathbb{R}^n$ est une fonction de classe $\mathscr{C}^1$, et que $f \colon \varphi(D) \longrightarrow \mathbb{R}$ est continue, comme en dimension $1$. La matrice jacobienne $\mathrm{Jac}_{\textbf{t}}\varphi$ est l'analogue en dimension $n \geq 2$ de la dérivée d'une fonction. Plus explicitement, pour tout $\textbf{t} \in D$, comme $\varphi(\textbf{t}) \in \mathbb{R}^n$, on peut écrire $\varphi(\textbf{t}) = (\varphi_1(\textbf{t}), \ldots, \varphi_n(\textbf{t}))$, et alors
$$\mathrm{Jac}_{\textbf{t}}\varphi := \begin{pmatrix} \frac{\partial \varphi_1}{\partial t_1}(\textbf{t}) & \ldots & \frac{\partial \varphi_1}{\partial t_n}(\textbf{t}) \\ \vdots & & \vdots \\ \frac{\partial \varphi_n}{\partial t_1}(\textbf{t}) & \ldots & \frac{\partial \varphi_n}{\partial t_n}(\textbf{t}) \end{pmatrix}.$$
En dimension $1$, la jacobienne $\mathrm{Jac}_{t}\varphi$ n'est autre que la matrice $\begin{pmatrix} \varphi'(t) \end{pmatrix}$ dont le déterminant est bien $\varphi'(t)$. Les valeurs absolues qui apparaissent montrent en revanche qu'il y a un nouveau phénomène à prendre en compte, qui pourra contraindre à des hypothèses plus fortes sur nos fonctions.

Le pas d'intégration et la matrice jacobienne

Dans une intégrale simple, on avait vu que le nouveau pas était obtenu à partir des variations infinitésimales de $\varphi$. Comment justifier cette fois-ci qu'on s'attende à voir apparaître le déterminant jacobien de $\varphi$ ?

Tout d'abord, il faut savoir que le déterminant d'une matrice est très fortement lié aux volumes. Sa valeur absolue est en fait le facteur de dilatation permettant de passer du volume du parallélépipède unité au volume du parallélépipède image du parallélépipède unité par l'application linéaire naturellement associée à la matrice. Dans notre cas, rappelez-vous, on approche notre ensemble $D$ de départ par des pavés de plus en plus petits, et sur chaque pavé, on approche la fonction à intégrer par une constante qu'on multiplie par le volume du pavé. En effectuant notre changement de variables, il faut comprendre quelle est son influence sur le volume de nos pavés, infinitésimalement parlant.

Partons donc d'un pavé dans $\mathbb{R}^n$ de très petits côtés $dt_1,\ldots,dt_n$, et considérons son image par $\varphi$. Un des grands principes du calcul différentiel est d'approcher les fonctions (différentiables) par leur partie linéaire autour d'un point qui nous intéresse, approximation qui devient de plus en plus réaliste quand on se rapproche dudit point. En une dimension, cela donne $\varphi(t+dt) \simeq \varphi(t) + dt\varphi'(t)$ pour $dt$ tout petit. En dimension supérieure, la partie linéaire de $\varphi$ est sa différentielle, c'est-à-dire la matrice $\mathrm{Jac}_{\textbf{t}}\varphi$. Ainsi, on peut approcher $\varphi$ par l'application affine $$\textbf{t} \mapsto \varphi(\textbf{t}_0) + (\mathrm{Jac}_{\textbf{t}_0}\varphi)(\textbf{t})$$ pour un $\textbf{t}_0$ bien choisi. Dans ce cas, l'image du pavé de départ est aussi un pavé, et son volume ne dépend pas du facteur constant $\varphi(\textbf{t}_0)$. On est donc en train de chercher à déterminer le volume d'un pavé image par une application linéaire d'un pavé de côtés $dt_1,\ldots,dt_n$, c'est donc le déterminant de l'application linéaire multiplié par $dt_1\ldots dt_n$, c'est-à-dire $\left\lvert\det(\mathrm{Jac}_{\textbf{t}_0}\varphi)\right\rvert dt_1\ldots dt_n$.

Une autre façon de raisonner, plutôt que d'approcher directement $\varphi$ par sa partie linéaire, est de commencer par établir les coordonnées des sommets de notre pavé image par $\varphi$, qui n'est pas forcément un pavé mais qui sera approché comme tel. Prenons notre pavé initial tel qu'un de ses sommets est $\textbf{t} := (t_1,\ldots,t_n) \in \mathbb{R}^n$ et tel que les sommets qui lui sont adjacents sont donnés par $(t_1,\ldots, t_{i-1},t_i + dt_i,t_{i+1}, \ldots, t_n)$ où $dt_i$ est très petit. Par propriété du déterminant, le volume d'un pavé porté par les vecteurs $\textbf{u}_1,\ldots,\textbf{u}_n$ est la valeur absolue du déterminant de la matrice dont la $i^{\text{ème}}$ colonne est constituée des coordonnées de $\textbf{u}_i$. Ici, les vecteurs $\textbf{u}_i$ sont donnés par $$(t_1,\ldots, t_{i-1},t_i + dt_i,t_{i+1}, \ldots, t_n)-\textbf{t} = (0,\ldots,0,dt_i,0,\ldots,0).$$ On voit ici que le volume de notre pavé de départ est bien donné par le déterminant de la matrice $$\begin{pmatrix} dt_1 & 0 & & \ldots & & 0 \\ 0 & dt_2 & 0 & \ldots & & 0 \\ & & & & & \\ \vdots & & & \ddots & & \vdots \\ & & & & & \\ 0 & & \ldots & & 0 & dt_n \end{pmatrix},$$ à savoir $dt_1\ldots dt_n$.

Le "pavé" image par $\varphi$ est porté par les vecteurs $$\varphi(t_1,\ldots, t_{i-1},t_i + dt_i,t_{i+1}, \ldots, t_n) - \varphi(\textbf{t})$$ que l'on appellera $\textbf{v}_i$. Mais pour $dt_i$ très petit, $\textbf{v}_i$ est très proche du vecteur $(dt_i \frac{\partial \varphi_1}{\partial t_i}(\textbf{t}), \ldots,dt_i \frac{\partial \varphi_n}{\partial t_i}(\textbf{t}))$. Ainsi, on se retrouve à calculer le déterminant de la matrice $$\begin{pmatrix} dt_1 \frac{\partial \varphi_1}{\partial t_1}(\textbf{t}) & \ldots & dt_n \frac{\partial \varphi_1}{\partial t_n}(\textbf{t}) \\ \vdots & & \vdots \\ dt_1 \frac{\partial \varphi_n}{\partial t_1}(\textbf{t}) & \ldots & dt_n \frac{\partial \varphi_n}{\partial t_n}(\textbf{t}) \end{pmatrix},$$ qui, par multilinéarité du déterminant, n'est autre que $dt_1\ldots dt_n$ multiplié par le déterminant de la matrice jacobienne. Tout ceci est bien sûr à prendre avec des pincettes, car il faudrait rigoureusement justifier les approximations que nous avons faites, mais c'est une interprétation possible du phénomène.

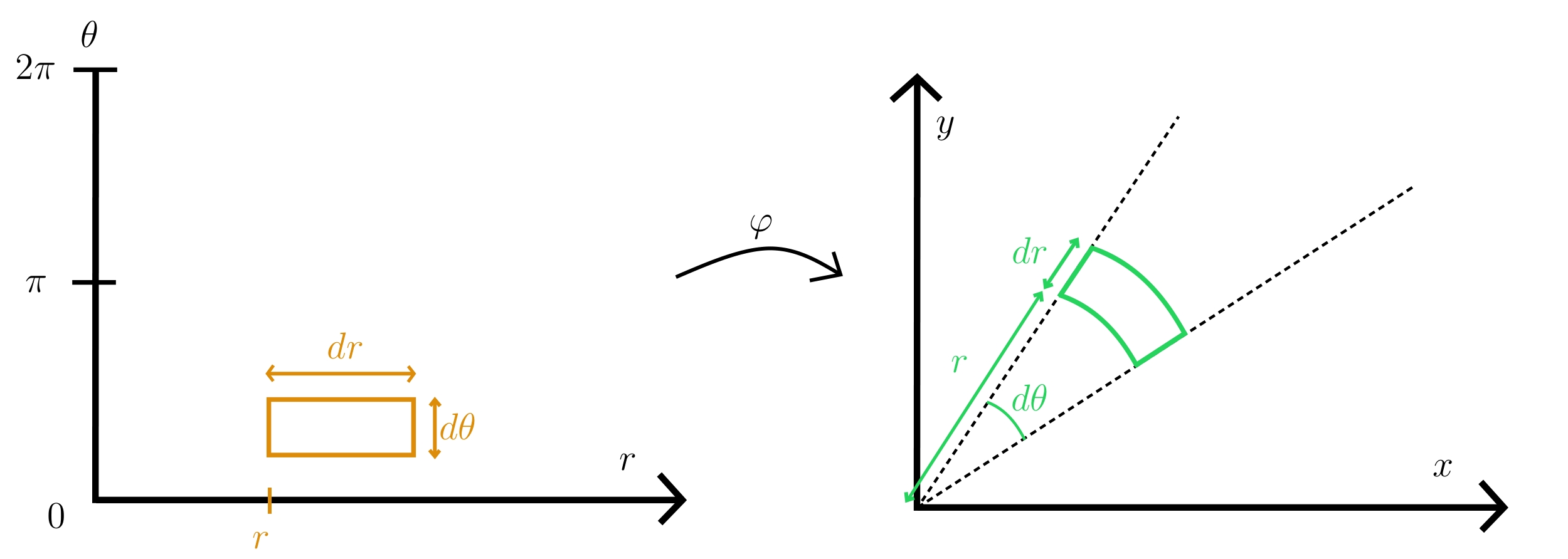
Un dernier commentaire sur l'apparition du déterminant jacobien : on peut aussi calculer directement le volume du "pavé" infinitésimal sans passer par des calculs de déterminant, lorsque cela n'est pas trop compliqué. L'exemple typique est le changement de variables en coordonnées polaires $$\varphi \colon \left \{ \begin{aligned} \rbrack 0, R \rbrack \times [0;2\pi[ & \longrightarrow \mathscr{D}(0,R) \\ (r,\theta) & \longmapsto (r\cos(\theta),r\sin(\theta)) \end{aligned} \right.,$$ où $R>0$ est un réel. Le paramètre $r$ encode la distance à l'origine, tandis que $\theta$ représente l'angle par rapport à la demi-droite des abscisses positives. L'image par $\varphi$ d'un petit pavé de côtés $dr$ et $d\theta$ est un secteur d'angle $d\theta$ intersecté avec une couronne d'épaisseur $dr$ à distance $r$ de l'origine, donc de superficie approximative $rdrd\theta$. En calculant la jacobienne de $\varphi$, on trouve bien que $\lvert\det(\mathrm{Jac}_{(r,\theta)}\varphi)\rvert = r$.

Orientation et bijectivité de $\varphi$

Premièrement, le changement de variable $\varphi$ est implicitement surjectif. En une dimension, le fait que $\varphi$ soit continue et atteigne les bornes de l'intervalle désiré implique par le théorème des valeurs intermédiaires que $\varphi$ parcourt tout l'intervalle. Mais de façon générale, quand on est face à une intégrale du type $\int_S f(\textbf{x})d\textbf{x}$, il faut bien que le changement de variables $\varphi \colon D \longrightarrow \varphi(D)$ désiré soit tel que $S = \varphi(D)$, puisqu'on veut parcourir tout l'ensemble $S$. Qu'en est-il de l'injectivité ? Est-ce que $\varphi$ peut passer plusieurs fois par le même endroit ?

Partant d'un sous-ensemble $D$ de $\mathbb{R}^n$, par exemple un carré dans $\mathbb{R}^2$, on peut se demander quelle influence cela aura sur l'intégrale $\int_D f(\textbf{x})d\textbf{x}$ de parcourir $D$ plutôt dans un sens, dans un autre, en tournant,... Heureusement, dès qu'on choisit $D$ raisonnable (borné en particulier) et que notre fonction $f$ n'explose pas dessus, l'intégrale est insensible à ce problème (d'ailleurs, quand on calcule la superficie d'un carré, on ne s'attend pas à ce que le résultat dépende de la façon dont on parcourt le carré !), à une subtilité près toutefois : un signe, qui apparaît selon l'orientation choisie.

Quand on doit aller d'un point $a$ à un point $b$ en dimension une, il n'y a qu'un chemin possible, le segment qui les relie. L'écriture $\int_a^b f(x)dx$ sous-entend qu'on commence en partant de $a$ et qu'on arrive à $b$. Peu importe qu'on aille vite ou lentement entre $a$ et $b$, on obtiendra le même résultat. En revanche, si on part de $b$ pour aller vers $a$, on voit qu'il va y avoir une différence : si l'on souhaite préserver la relation de Chasles, on a $$\int_a^b f(x)dx + \int_b^a f(x)dx = \int_a^a f(x)dx = 0,$$
ce dont on infère $$\int_a^b f(x)dx = -\int_b^a f(x)dx.$$
Ainsi, le fait d'aller dans un sens ou dans l'autre introduit un signe, qui traduit un changement d'orientation. Ce qui est pratique en dimension $1$, c'est que le changement d'orientation se marie bien avec la notation $\int_a^b$. Et surtout, la magie qui opère dans ce cas-là est que la non-bijectivité d'une fonction continue en une dimension se traduit par une alternance de phases de croissance et de décroissance (éventuellement de phases de constance, mais alors la dérivée est nulle et donc la contribution à l'intégrale est nulle aussi dans la formule du changement de variable). Ainsi, lorsqu'on parcourt un nombre pair de fois le même chemin, exactement la moitié se fera dans un sens et l'autre moitié dans l'autre sens ! Ce qui se compense parfaitement avec le signe introduit par l'orientation. Parcourir un nombre pair de fois le même chemin n'apporte donc rien à l'intégrale, tandis que le parcourir un nombre impair de fois revient à le parcourir une fois, dans le sens qui est majoritaire.

Mais dès qu'on a plus d'espace, il est tout à fait possible de passer deux fois par le même point sans faire demi-tour : il suffit de tourner ! Pour peu de tourner dans le bon sens, on ne changera pas l'orientation en procédant ainsi, donc au lieu d'assister à une compensation, on comptera deux fois le même passage. Il paraît raisonnable dans ces conditions de demander à ce que notre changement de variables soit injectif, donc bijectif...

Exemple 4. Dans le plan $\mathbb{R}^2$, considérons l'ensemble $D := [0;1] \times [0;4\pi]$, le changement de variables $\varphi \colon \left \{ \begin{aligned} D & \longrightarrow \varphi(D) \subseteq \mathbb{R}^2 \\ (s,t) & \longmapsto (e^s\cos(t), e^s(\sin(t)) \end{aligned} \right.$, et l'intégrale $\int_{\varphi(D)} (x^2 + y^2) d(x,y)$. La jacobienne de $\varphi$ en $(s,t) \in D$ est donnée par
$$\mathrm{Jac}_{(s,t)}\varphi = \begin{pmatrix} e^s\cos(t) & -e^s\sin(t) \\ e^s\sin(t) & e^s\cos(t) \end{pmatrix},$$
dont le déterminant est $e^{2s}(\cos^2(t) + \sin^2(t)) = e^{2s} >0$.

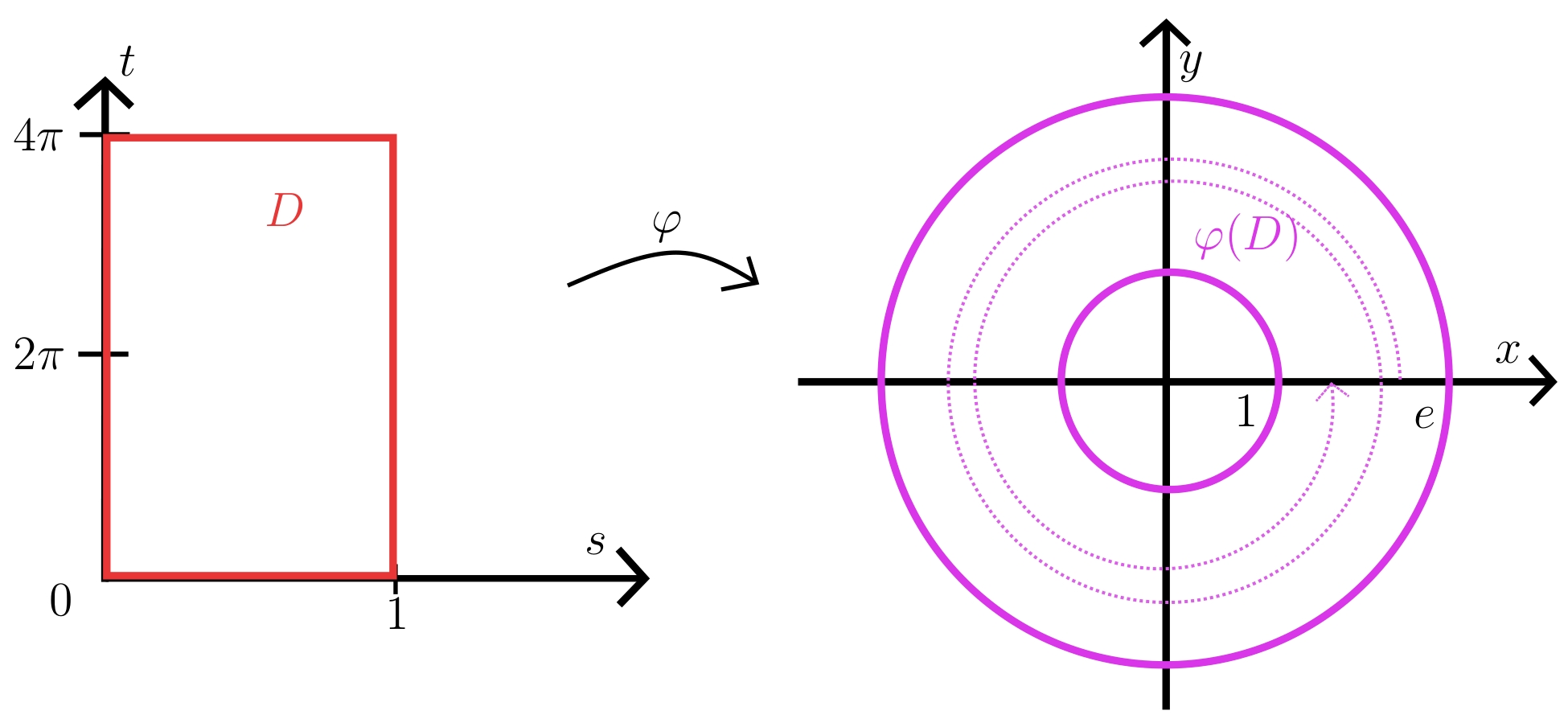
L'intégrale qu'on obtiendrait avec le changement de variables $\varphi$ (qui n'est pas injectif !) est $\int_D e^{2s} e^{2s}d(s,t)$. À l'aide du théorème de Fubini, on décompose cette intégrale bidimensionnelle en
$$\int_D e^{2s} e^{2s}d(s,t) = \int_0^{4\pi} dt \int_0^1 e^{4s}ds = 4\pi \frac{e^4-1}{4}.$$
    
De l'autre côté, on peut calculer aussi l'intégrale $\int_{\varphi(D)} (x^2 + y^2) d(x,y)$ grâce au classique changement de variables en coordonnées polaires, qui vérifie les bonnes hypothèses. L'ensemble $\varphi(D)$ est une couronne centrée en l'origine, de cercle intérieur de rayon $1$ et de cercle extérieur de rayon $e$. Soit $\psi \colon \left \{ \begin{aligned} \lbrack1;e\rbrack \times [0;2\pi[ & \longrightarrow \varphi(D) \\ (r,\theta) & \longmapsto (r\cos(\theta),r\sin(\theta)) \end{aligned} \right.$. La jacobienne de $\psi$ au point $(r,\theta)$ est donc $$\mathrm{Jac}_{(r,\theta)}\psi = \begin{pmatrix} \cos(\theta) & -r\sin(\theta) \\ \sin(\theta) & r\cos(\theta) \end{pmatrix},$$
dont le déterminant est $r\cos^2(\theta) + r\sin^2(\theta) = r > 0$. On obtient ainsi
$$\int_{\varphi(D)} (x^2 + y^2)d(x,y) = \int_{[1;e]\times[0;2\pi[} r^2 (rdrd\theta) = 2\pi \int_{1}^{e}  r^3 dr = 2\pi\frac{e^4-1}{4}.$$
    
Le résultat obtenu dans le premier cas est le double du deuxième, puisqu'on a parcouru deux fois la couronne $\varphi(D)$ avec le changement de variables $\varphi$.

Remarquons qu'en prenant $D = [0;1] \times [0;2k\pi]$ avec $k \geq 1$ un entier dans l'exemple précédent, on trouve $k$ fois le résultat attendu avec le changement de variables $\varphi$, puisqu'on fait $k$ fois le tour de la couronne.

En extrapolant, on peut même arriver à créer ce genre de problème en dimension $1$, dès lors qu'on est plongé dans un espace de dimension $2$. Par exemple, si on veut intégrer une fonction non-pas le long d'un segment mais le long d'un cercle, le même phénomène de rotation peut arriver.

Exemple 5. On note $\mathscr{C}(0;1)$ le cercle centré en l'origine de rayon $1$ dans $\mathbb{R}^2$, et on considère $D_k = [0;1] \times [0;2k\pi[$ où $k \geq 1$ est entier. Soit $\psi_k$ le changement de variables en coordonnées polaires avec $k$ tours $$\psi_k \colon \left \{ \begin{aligned} D_k & \longrightarrow \mathscr{C}(0;1) \\ (r,\theta) & \longmapsto (r\cos(\theta),r\sin(\theta)) \end{aligned} \right..$$ Alors de la même façon que précédemment, on trouve via le "vrai" changement de variables $\psi_1$
$$\int_{\mathscr{C}(0,1)} (x^2 + y^2)d(x,y) = \int_{0}^{2\pi}d\theta \int_{0}^{1}r^2rdr = 2\pi \frac{1}{4} = \frac{\pi}{2},$$
tandis que via $\psi_k$ on arrive à l'intégrale
$$\int_{0}^{2k\pi}d\theta \int_{0}^{1}r^2rdr = 2k\pi \frac{1}{4} = k\frac{\pi}{2}.$$

En fait, on peut se passer de l'hypothèse d'injectivité de $\varphi$ à condition de modifier la formule du changement de variables de façon à tenir compte du nombre de fois qu'on passe plusieurs fois par le même endroit. Pour autant, cela implique justement de connaître suffisamment $\varphi$ pour dire combien de fois on passe par tels ou tels points, ce qui limite son intérêt pratique.

Orientation et difféomorphisme

Sans rentrer dans les détails, le changement d'orientation se repère par un changement de signe dans la fonction $\textbf{t} \mapsto \det(\mathrm{Jac}_{\textbf{t}}\varphi)$, qui dépend continûment de $\textbf{t}$ (on le voit bien en dimension $1$ : le signe de la dérivée indique précisément qu'on croît ou qu'on décroît). On a constaté en sous-section 3.3 que les problèmes d'orientation nous imposent déjà le caractère bijectif du changement de variables $\varphi$. Cependant, il n'est pas clair que cet aspect bijectif suffise à prévenir d'un changement d'orientation en cours de route. L'exemple suivant est à deux doigts de vérifier un tel phénomène, ce qui incite à la prudence.

Exemple 6. Considérons l'application $\varphi \colon \left \{ \begin{aligned} \mathbb{R}^2 & \longrightarrow \mathbb{R}^2 \\ (x,y) & \longmapsto (x^3,y) \end{aligned} \right.$. Elle est clairement bijective, et sa matrice jacobienne au point $(x,y)$ est
$$\mathrm{Jac}_{(x,y)}\varphi = \begin{pmatrix} 3x^2 & 0 \\ 0 & 1 \end{pmatrix}$$
de déterminant $3x^2$. Le déterminant est positif, mais s'annule sur toute la droite d'équation $x = 0$.

La bijectivité n'implique pas que la différentielle ne s'annule jamais (c'est l'exemple de la fonction cube), cependant on voit bien en dimension $1$ que si la dérivée s'annule en changeant de signe, la fonction de départ n'est pas injective. Mais est-ce toujours le cas en dimension supérieure, c'est-à-dire est-ce que l'injectivité de $\varphi$ implique que le déterminant jacobien ne peut pas changer de signe ? Le résultat suivant, que l'on peut trouver à la fin de 1 (proposition 6.1) ou dans les livres centrés sur le degré topologique, répond exactement à cette question.

Théorème. Soit $\varphi \colon D \subseteq \mathbb{R}^n \longrightarrow \mathbb{R}^n$ une application injective et différentiable, où $D$ est un ouvert borné et "connexe" (c'est-à-dire en un seul morceau). Alors son déterminant jacobien est de signe constant.

Par conséquent, quitte à travailler séparément sur toutes les composantes connexes de $D$, le changement de variable $\varphi$ introduira au pire un et un seul changement d'orientation (global), mais il ne peut pas y avoir de cas pathologiques pour lesquels on assiste à plusieurs changements d'orientation lorsqu'on fait varier $\textbf{t}$. Cela simplifie le problème, car alors il n'y a à nouveau que deux cas à considérer : le cas où on préserve l'orientation, et celui où on l'inverse complètement en introduisant un signe.

Cependant, le théorème précédent est un résultat fort de topologie qui manipule des notions très avancées (théorème de l'invariance du domaine, degré topologique d'une application continue). Ou bien on transpire beaucoup pour le démontrer, ou bien on se contente d'hypothèses plus restrictives pour arriver à nos fins. Un cas nettement plus simple est celui d'un changement de variables dont le déterminant jacobien ne s'annule jamais : puisqu'il dépend continûment de $\textbf{t}$ par hypothèse, on ne peut pas sauter du bloc des réels strictement négatifs à celui des positifs et inversement, donc le signe sera constant. Or ce cas est justement atteint lorsque $\varphi$ est supposé être un $\mathscr{C}^1$-difféomorphisme, c'est-à-dire une application bijective de classe $\mathscr{C}^1$ (jusque-là on n'a rien changé) et dont l'inverse est aussi de classe $\mathscr{C}^1$. La démonstration tient en quelques lignes, il suffit de différencier l'identité écrite comme $\varphi \circ \varphi^{-1}$ et comme $\varphi^{-1} \circ \varphi$ pour expliciter l'inverse de la matrice jacobienne.

Il ne reste plus à présent qu'à comprendre comment régler le cas où on inverse globalement l'orientation. En dimension $1$, l'écriture des bornes de l'intégrale est pratique, mais c'est impossible d'écrire quelque chose de similaire en dimensions supérieures.

Restons en dimension $1$ pour le moment, et supposons que $\varphi$ est bijectif. En prenant $a<b$ deux réels, le phénomène d'interversion des bornes dans l'intégrale apparaît lorsque $\varphi(b) < \varphi(a)$ (le cas où $\varphi$ est décroissant). Dans la deuxième situation, on obtient
\begin{align*} \int_{\varphi(b)}^{\varphi(a)} f(x)dx & = \int_b^a f \circ \varphi(t) \varphi'(t) dt =  \int_a^b f \circ \varphi(t) (-\varphi'(t)) dt \\ & = \int_a^b f \circ \varphi(t) \left\lvert\varphi'(t)\right\rvert dt.\end{align*}
L'intégrale de départ et celle d'arrivée sont parcourues dans le même sens, et l'égalité est cohérente avec le cas où $\varphi$ est croissante, donc on peut réécrire la formule du changement de variable comme suit, avec $I := [a,b]$ :

$$\int_{\varphi(I)} f(x)dx = \int_I f \circ \varphi(t) \left\lvert\varphi'(t)\right\rvert dt.$$

L'écriture $\int_I$ signifie qu'on a enlevé la dépendance au sens de parcours, i.e. toutes les intégrales écrites sous cette forme parcourent l'intervalle dans le même sens, de la gauche vers la droite par convention. Ainsi, si $\varphi$ est strictement décroissante et si $a<b$, on a $\int_{\varphi([a,b])} = \int_{\varphi(b)}^{\varphi(a)}$.

De cette manière, on a résolu le problème du sens de parcours en dimension $1$. Il ne reste plus qu'à faire pareil en dimensions supérieures : si $D \subseteq \mathbb{R}^n$, alors la notation $\int_D$ sous-entendra (selon nos conventions) qu'on choisit une orientation de $D$ de telle sorte que l'intégrale $\int_D d\textbf{x}$ soit positive. C'est cette convention qui est implicitement utilisée lorsqu'on écrit la formule convoitée
$$\int_{\varphi(D)} f(\textbf{x})d\textbf{x} = \int_D f \circ \varphi(\textbf{t}) \left\lvert\det(\mathrm{Jac}_{\textbf{t}}\varphi)\right\rvert d\textbf{t}.$$

Remarquons que l'intégrale $\int_D d\textbf{x}$ n'est autre que le volume de $D$ ! On approche ici la théorie de la mesure (il faut d'ailleurs que $D$ soit un sous-ensemble dit "mesurable" pour que $\int_D$ ait un sens), dans laquelle on ne veut pas que l'orientation ait une influence sur nos intégrales, typiquement le changement de variables $(x,y) \mapsto (y,x)$ de déterminant jacobien $-1$ ne doit pas changer le résultat attendu.

Un dernier mot sur la théorie

Nous avons donc tout en main pour énoncer une version possible du théorème du changement de variables en dimension $n \geq 1$ :

Théorème. Soit $U \subseteq \mathbb{R}^n$ un ouvert borné, soit $\varphi \colon U \longrightarrow \varphi(U) \subseteq \mathbb{R}^n$ un $\mathscr{C}^1$-difféomorphisme, et soit $f \colon \varphi(U) \longrightarrow \mathbb{R}$ une application continue et bornée. Alors on a
$$\int_{\varphi(U)} f(\textbf{x})d\textbf{x} = \int_U f \circ \varphi(\textbf{t}) \left\lvert\det(\mathrm{Jac}_{\textbf{t}}\varphi)\right\rvert d\textbf{t}.$$

On a déjà remarqué que les hypothèses pouvaient être allégées : le fait que $\varphi^{-1}$ ne soit pas de classe $\mathscr{C}^1$ est possible, de même l'injectivité peut être omise si on modifie la formule conséquemment. Selon le contexte, les énoncés peuvent différer légèrement : si on considère des formes différentielles, la formule sera traduite dans ce cadre; si on est en théorie de la mesure et qu'on considère des intégrales de Lebesgue, on parlera pour $U$ de sous-ensembles mesurables, etc.

Et au fait, quelle démonstration pour ce théorème ? La plus "classique" est assez lourde à mettre en place, et par conséquent il n'est pas toujours aisé de la trouver dans la littérature car souvent admise. Je reprends ici celle qu'on peut trouver dans 2, pages 688 à 690, en la réorganisant pour mieux mettre en lumière les principales étapes : se ramener à des pavés, morceler ces pavés de plus en plus finement jusqu'à atteindre l'échelon infinitésimal, puis justifier l'apparition du déterminant jacobien à l'aide des propriétés locales des éléments de volume.

Proposition. Pour démontrer le théorème, il suffit de montrer que
$$\int_{\varphi(P)} f(\textbf{x})d\textbf{x} = \int_P f \circ \varphi(\textbf{t}) \left\lvert\det(\mathrm{Jac}_{\textbf{t}}\varphi)\right\rvert d\textbf{t}$$
où $P \subseteq \mathbb{R}^n$ est un pavé, $\varphi \colon P \longrightarrow \varphi(P)$ est un $\mathscr{C}^1$-difféomorphisme et $f \colon \varphi(P) \longrightarrow (\mathbb{R}_+)^n$ est une application continue, bornée et positive.

Démonstration.

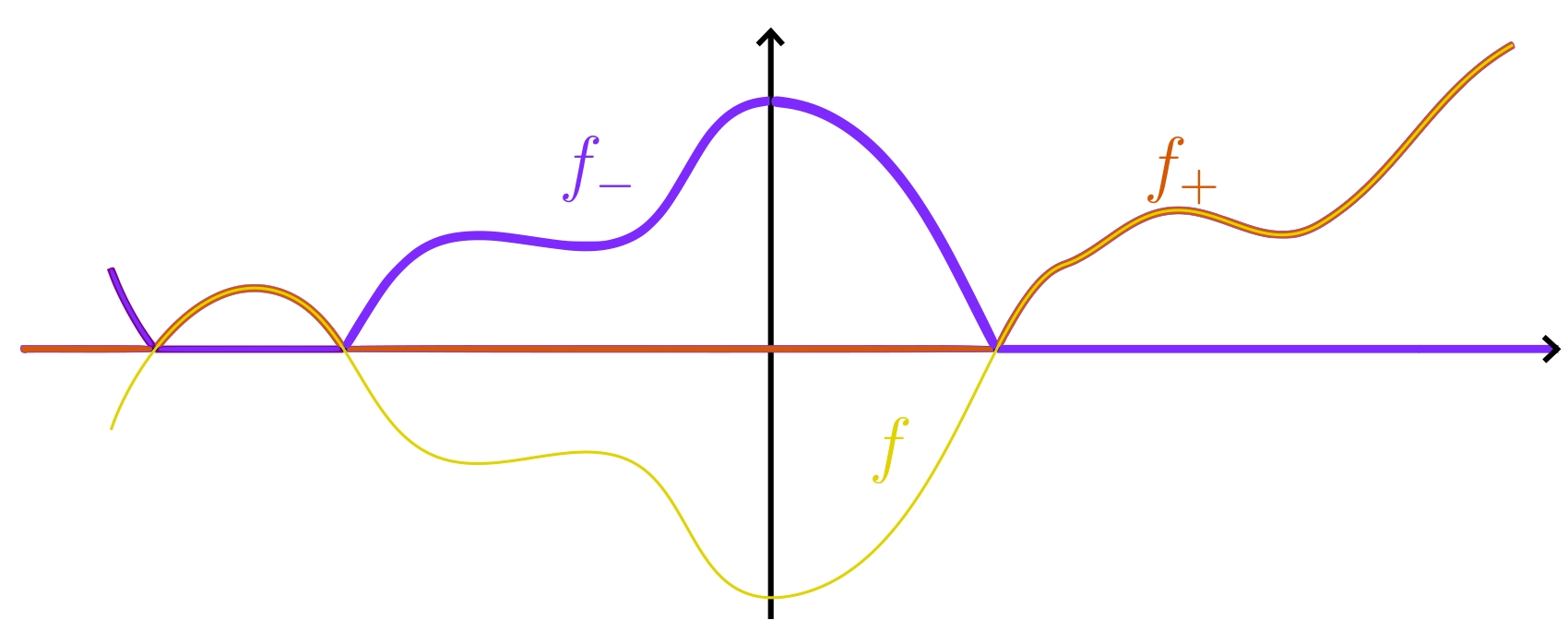
Soit $f \colon \varphi(P) \longrightarrow \mathbb{R}^n$ une application continue. On peut écrire $f = f_+ - f_-$ où $f_+ := \max(f,0)$ est sa partie positive et $f_- := \max(-f,0)$ est sa partie négative. Ces deux dernières fonctions sont bien positives, donc si la formule du changement de variables s'applique à elles, elle s'applique aussi à $f$ par linéarité de l'intégrale.

Enfin, soit $U \subseteq \mathbb{R}^n$ un ouvert borné. Supposons que le théorème soit vrai pour les pavés. Alors il est aussi vrai pour toutes les réunions finies et disjointes de pavés, toujours par linéarité de l'intégrale. Pour atteindre l'ouvert $U$ à partir de pavés, on procède comme en sous-section 3.1 en morcelant $U$ en un pavage exhaustif (un tel pavage existe, on peut en expliciter, cf. 1, page 297) : $U = \bigcup_{i = 0}^{\infty} K_i$ où les $K_i$ sont des réunions finies de pavés d'intérieurs deux à deux disjoints. Le fait que les $K_i$ puissent s'intersecter sur leurs bords importe peu car ces bords sont négligeables, autrement dit l'intégrale de $f$ sur ces bords est nulle et donc ne contribue pas à l'intégrale. Le théorème du changement de variables s'applique pour chaque $K_i$, et en faisant tendre $i$ vers l'infini (en toute rigueur, avec un argument du type "théorème de convergence dominée"), on obtient bien l'énoncé pour $U$. $\square$

L'intérêt de considérer des fonctions positives est de simplifier les calculs. Se ramener à des pavés est très pratique car ils sont beaucoup plus faciles à subdiviser, et leur volume est plus facilement calculable. Le schéma de preuve pour le cas des pavés est le suivant : le déterminant jacobien traduisant l'intervention de dérivées, on subdivise notre pavé de départ de plus en plus finement, de sorte à pouvoir approcher les volumes des images par $\varphi$ des petits pavés par ceux des images par la partie linéaire de $\varphi$.

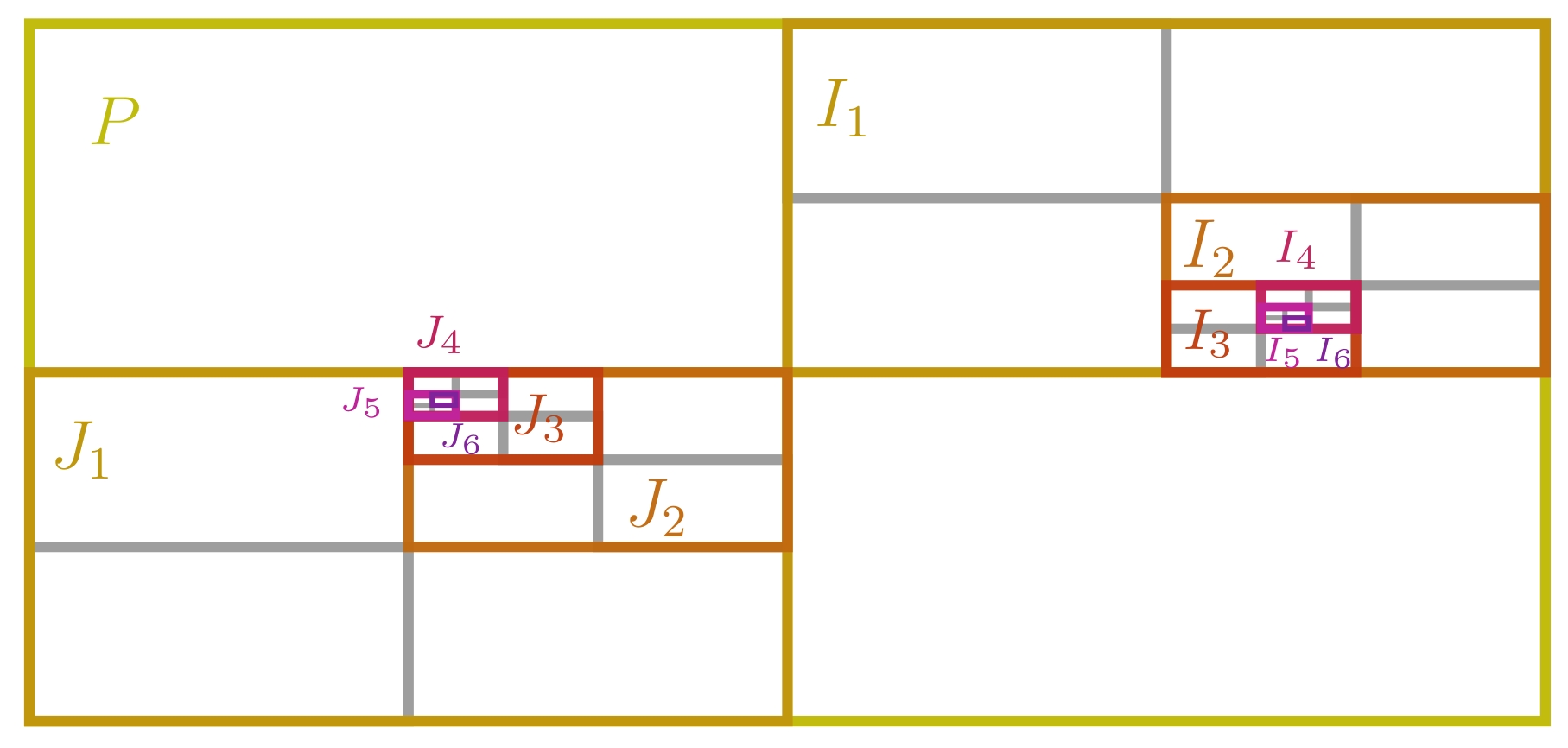
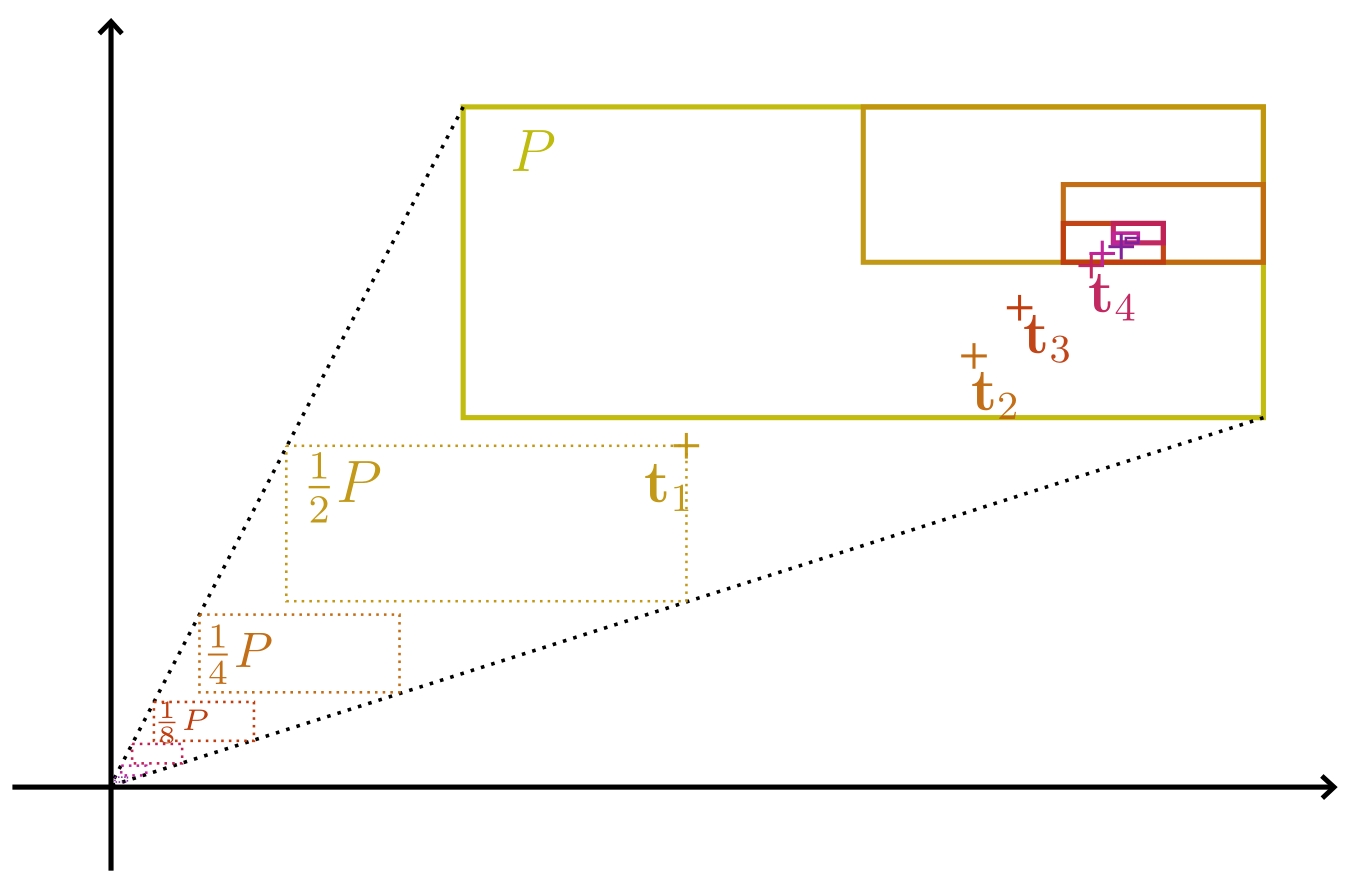
Démonstration du théorème. Soit $P \subseteq \mathbb{R}^n$ un pavé. Soit $$A := \frac{1}{\mathrm{Vol}(P)}\left( \int_{\varphi(P)} f(\textbf{x})d\textbf{x} - \int_P g(\textbf{t}) d\textbf{t} \right)$$ où $g \colon P \longrightarrow (\mathbb{R}_+)^n$ est la fonction définie par $g(\textbf{t}) := f \circ \varphi(\textbf{t}) \left\lvert\det(\mathrm{Jac}_{\textbf{t}}\varphi)\right\rvert$. Notre objectif est de montrer que $A = 0$.
    
Commençons par découper notre pavé $P$ en $2^n$ sous-pavés $P_k$ deux fois plus petits et d'intérieurs disjoints (si $P$ est un cube, on aura ainsi $8$ sous-cubes). Comme dit dans la preuve précédente, la contribution des bords des sous-pavés à l'intégrale est nulle, donc on peut écrire
$$\sum_{k = 1}^{2^n} \int_{\varphi(P_k)} f(\textbf{x})d\textbf{x} = \int_{\varphi(P)} f(\textbf{x})d\textbf{x} = \int_{P} (g(\textbf{t}) + A) d\textbf{t} = \sum_{k = 1}^{2^n} \int_{P_k} (g(\textbf{t}) + A)d\textbf{t}.$$
    
Puisqu'il y a le même nombre de termes dans les deux sommes, qui sont égales, il existe deux indices $k_1$ et $k_2$ tels que
$$\int_{\varphi(P_{k_1})} f(\textbf{x})d\textbf{x} \leq \int_{P_{k_1}} (g(\textbf{t}) + A)d\textbf{t} ~~~~ \text{et} ~~~~ \int_{\varphi(P_{k_2})} f(\textbf{x})d\textbf{x} \geq \int_{P_{k_2}} (g(\textbf{t}) + A)d\textbf{t},$$
ce dont on déduit les inégalités
$$\frac{\mathrm{Vol}(\varphi(P_{k_1}))}{\mathrm{Vol}(P_{k_1})}\min_{\varphi(P_{k_1})} f - \max_{P_{k_1}} g \leq A \leq \frac{\mathrm{Vol}(\varphi(P_{k_2}))}{\mathrm{Vol}(P_{k_2})}\max_{\varphi(P_{k_2})} f - \min_{P_{k_2}} g.$$
    
Posons $I_0 = J_0 := P$ et $I_1 := P_{k_1}$, $J_1 := P_{k_2}$. On itère à présent le même procédé sur $I_1$ et $J_1$ : on les morcelle tous les deux en $2^n$ sous-pavés $I_{1,k}$ et $J_{1,k}$, puis on déduit des inégalités
\begin{align*}
   & \sum_{k = 1}^{2^n} \int_{\varphi(I_{1,k})} f(\textbf{x})d\textbf{x} \leq \sum_{k = 1}^{2^n} \int_{I_{1,k}} (g(\textbf{t}) + A)d\textbf{t} \\
   \text{et} ~~~~ & \sum_{k = 1}^{2^n} \int_{\varphi(J_{1,k})} f(\textbf{x})d\textbf{x} \geq \sum_{k = 1}^{2^n} \int_{J_{1,k}} (g(\textbf{t}) + A)d\textbf{t}
\end{align*}
l'existence de deux indices $k_1'$ et $k_2'$ tels que
$$\int_{\varphi(I_{1,k_1'})} f(\textbf{x})d\textbf{x} \leq \int_{I_{1,k_1'}} (g(\textbf{t}) + A)d\textbf{t} ~~~~ \text{et} ~~~~ \int_{\varphi(J_{1,k_2'})} f(\textbf{x})d\textbf{x} \geq \int_{J_{1,k_2'}} (g(\textbf{t}) + A)d\textbf{t}.$$

Par récurrence, on construit ainsi deux suites de pavés emboîtés $(I_k)_{k \in \mathbb{N}}$ et $(J_k)_{k \in \mathbb{N}}$ tels que pour tous $k \geq 0$ :
\begin{align*}
    & \int_{\varphi(I_k)} f(\textbf{x})d\textbf{x} \leq \int_{I_k} (g(\textbf{t}) + A)d\textbf{t} \\ \text{et} ~~~~ & \int_{\varphi(J_k)} f(\textbf{x})d\textbf{x} \geq \int_{J_k} (g(\textbf{t}) + A)d\textbf{t}
\end{align*}
d'où découlent les inégalités

 

 

$$\frac{\mathrm{Vol}(\varphi(I_k))}{\mathrm{Vol}(I_k)}\min_{\varphi(I_k)} f - \max_{I_k} g \leq A \leq \frac{\mathrm{Vol}(\varphi(J_k))}{\mathrm{Vol}(J_k)}\max_{\varphi(J_k)} f - \min_{J_k} g,$$
valables pour tous $k \geq 0$.
    
Les $I_k$ forment une suite décroissante de pavés, et on peut démontrer que leur intersection est un point, que l'on appellera $\textbf{t}_I$. De même, l'intersection de tous les $J_k$ est un point, disons $\textbf{t}_J$. Par continuité de $f$ et de $g$, on sait que $\min_{\varphi(I_k)} f \underset{k \to \infty}{\longrightarrow} f(\varphi(\textbf{t}_I))$, $\max_{\varphi(J_k)} f \underset{k \to \infty}{\longrightarrow} f(\varphi(\textbf{t}_J))$, $\max_{I_k} g \underset{k \to \infty}{\longrightarrow} g(\textbf{t}_I)$ et $\min_{J_k} g \underset{k \to \infty}{\longrightarrow} g(\textbf{t}_J)$. Il ne reste plus qu'à étudier les deux rapports $\frac{\mathrm{Vol}(\varphi(I_k))}{\mathrm{Vol}(I_k)}$ et $\frac{\mathrm{Vol}(\varphi(J_k))}{\mathrm{Vol}(J_k)}$. Pour ne pas surcharger cette démonstration, nous montrerons dans la proposition suivante que ces deux rapports tendent respectivement vers $\left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert$ et $\left\lvert\det(\mathrm{Jac}_{\textbf{t}_J} \varphi)\right\rvert$. Ceci permet de conclure comme suit, par définition de $g = f \circ \varphi \cdot \left\lvert\det(\mathrm{Jac}_{-} \varphi)\right\rvert$ :

    \begin{align*}
            \frac{\mathrm{Vol}(\varphi(I_k))}{\mathrm{Vol}(I_k)}\min_{\varphi(I_k)} f - \max_{I_k} g \leq A & \leq \frac{\mathrm{Vol}(\varphi(J_k))}{\mathrm{Vol}(J_k)}\max_{\varphi(J_k)} f - \min_{J_k} g \\
            \downarrow \scriptstyle{k \to \infty} \hspace{3cm} & \hspace{3cm} \downarrow \scriptstyle{k \to \infty} \\
            \left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert f(\varphi(\textbf{t}_I)) - g(\textbf{t}_I) = 0 \hspace{1cm} & \hspace{1cm} 0 = \left\lvert\det(\mathrm{Jac}_{\textbf{t}_J} \varphi)\right\rvert f(\varphi(\textbf{t}_J)) - g(\textbf{t}_J)
        \end{align*}

    
Par théorème d'encadrement, la quantité $A$ est nulle, c'est-à-dire que $\int_{\varphi(P)} f(\textbf{x})d\textbf{x} = \int_P g(\textbf{t}) d\textbf{t}$, et le théorème est démontré. $\square$

La proposition suivante, essentielle pour la démonstration du théorème, fait le lien avec la sous-section 3.2 en donnant une version rigoureuse des heuristiques présentées alors.

Proposition. Dans les notations de la démonstration précédente, les rapports $\frac{\mathrm{Vol}(\varphi(I_k))}{\mathrm{Vol}(I_k)}$ et $\frac{\mathrm{Vol}(\varphi(J_k))}{\mathrm{Vol}(J_k)}$ tendent respectivement vers $\left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert$ et $\left\lvert\det(\mathrm{Jac}_{\textbf{t}_J} \varphi)\right\rvert$.

Remarque. En dimension $1$, $I_k$ serait un intervalle, disons $[a_k,b_k]$, et la proposition revient à dire que le rapport $\left\lvert\frac{\varphi(b_k) - \varphi(a_k)}{b_k-a_k}\right\rvert$ tend vers $\left\lvert\varphi'(t_I)\right\rvert$, où $a_k, b_k \underset{k \to \infty}{\longrightarrow} t_I$.

Démonstration. Commençons par annoncer que la preuve sera identique pour chacun des deux rapports, nous ne considérerons donc que le premier.
Ensuite, notons $\varPhi \colon P \longrightarrow \mathbb{R}^n$ l'application affine définie par $$\varPhi(\textbf{t}) := \varphi(\textbf{t}_I) + \mathrm{Jac}_{\textbf{t}_I}\varphi(\textbf{t} - \textbf{t}_I).$$ C'est l'application affine qui approche le mieux $\varphi$ autour de $\textbf{t}_{I}$. Son intervention dans le raisonnement provient du fait que pour tout pavé $Q \subseteq \mathbb{R}^n$, on a $$\mathrm{Vol}(\varPhi(Q)) = \left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert \mathrm{Vol}(Q).$$
L'idée de la preuve va être d'encadrer chaque pavé $I_k$ par des pavés de plus en plus proches de $I_k$, contenant ou contenus dans $I_k$. On peut alors montrer que les volumes des pavés approximateurs images par $\varPhi$ vont encadrer (pour $k$ assez grand) le volume de $\varphi(I_k)$. Les inégalités obtenues donneront asymptotiquement le résultat souhaité.
   

C'est parti : prenons $M$ et $N$ deux pavés tels que $M \subset P \subset N$, et tels que leurs bords soient disjoints; autrement dit, $M$ est inclus dans l'intérieur de $P$ et $P$ est inclus dans l'intérieur de $N$. Ceci implique qu'il existe deux réels $\mu, \nu > 0$ tels que tout point de $M$ est à distance au moins $\mu$ du bord de $P$ et tout point de $P$ est à distance au moins $\nu$ du bord de $N$. [On conclura la preuve en prenant $M$ et $N$ arbitrairement proches de $P$.]

À $k$ fixé, le pavé $I_k$ est un translaté de $\frac{1}{2^k}P$, par construction. Il existe donc $\textbf{t}_k \in \mathbb{R}^n$ tel que $I_k = \textbf{t}_k + \frac{1}{2^k}P$. On définit de la même façon
$$M_k := \textbf{t}_k + \frac{1}{2^k}M ~~~~ \text{et} ~~~~ N_k := \textbf{t}_k + \frac{1}{2^k}N,$$
de sorte que $M_k \subset I_k \subset N_k$ pour tout $k$.

Remarquons que la suite $(\textbf{t}_k)_{k \in \mathbb{N}}$ converge dans $\mathbb{R}^n$ vers $\textbf{t}_I$. En effet, $\textbf{t}_I \in I_k$ pour tout $k$, donc il existe $\textbf{t}_k' \in P$ tel que $\textbf{t}_I = \textbf{t}_k + \frac{1}{2^k}\textbf{t}_k'$, autrement dit $\textbf{t}_I - \textbf{t}_k = \frac{1}{2^k}\textbf{t}_k'$. Puisque $P$ est borné, la norme de $\textbf{t}_k$ est elle aussi bornée par une constante $c \in \mathbb{R}_+^{\times}$, et donc
$$\left\lVert\textbf{t}_I - \textbf{t}_k\right\rVert \leq \frac{c}{2^k} \underset{k \to \infty}{\longrightarrow} 0.$$

Montrons qu'il existe $k_0 \in \mathbb{N}$ tel que pour tout $k \geq k_0$, on ait $\varPhi(M_k) \subseteq \varphi(I_k) \subseteq \varPhi(N_k)$. À nouveau, nous ne montrerons que la première inclusion, l'argument se recopiant mot pour mot pour la seconde.
    
Soit $\textbf{y}_k \in M_k$. En faisant un tel choix pour tout $k \in \mathbb{N}$, on construit une suite de points dans $\mathbb{R}^n$ qui converge vers $\textbf{t}_I$; plus précisément, via l'inégalité triangulaire,
$$\left\lVert\textbf{y}_k - \textbf{t}_I\right\rVert \leq \left\lVert\textbf{y}_k - \textbf{t}_k\right\rVert + \left\lVert\textbf{t}_k - \textbf{t}_I\right\rVert \leq \frac{c'}{2^k} \underset{k \to \infty}{\longrightarrow} 0$$ pour un certain $c' \in \mathbb{R}_+^{\times}$.
    
Regarder si $\varPhi(\textbf{y}_k)$ est dans $\varphi(I_k)$ est équivalent à voir si $\varphi^{-1}\circ \varPhi(y_k)$ appartient à $I_k$. L'application $\varphi^{-1} \circ \varPhi$ étant de classe $\mathscr{C}^1$, on peut faire un développement limité en $\textbf{t}_I$ et obtenir que
$$\varphi^{-1} \circ \varPhi(\textbf{y}_k) = \varphi^{-1} \circ \varPhi(\textbf{t}_I) + (\mathrm{Jac}_{\textbf{t}_I} (\varphi^{-1} \circ \varPhi))(\textbf{y}_k-\textbf{t}_I) + \varepsilon(\textbf{y}_k - \textbf{t}_I)$$
où $\varepsilon \colon P \longrightarrow \mathbb{R}^n$ est une application vérifiant $\frac{\left\lVert\varepsilon(\textbf{t}-\textbf{t}_I)\right\rVert}{\left\lVert\textbf{t}-\textbf{t}_I\right\rVert} \underset{\textbf{t} \to \textbf{t}_I}{\longrightarrow} 0$.
    
Par dérivation composée, on a
\begin{align*}
    \mathrm{Jac}_{\textbf{t}_I} (\varphi^{-1} \circ \varPhi) & = \mathrm{Jac}_{\varPhi(\textbf{t}_I)} \varphi^{-1} \cdot \mathrm{Jac}_{\textbf{t}_I} \varPhi \\ & =  \mathrm{Jac}_{\varphi(\textbf{t}_I)} \varphi^{-1} \cdot \mathrm{Jac}_{\textbf{t}_I} \varphi \\ & = (\mathrm{Jac}_{\textbf{t}_I} \varphi)^{-1} \cdot \mathrm{Jac}_{\textbf{t}_I} \varphi = id.
\end{align*}
    
Par conséquent, $\varphi^{-1} \circ \varPhi(\textbf{y}_k) = \varphi^{-1} \circ \varPhi(\textbf{t}_I) + (\textbf{y}_k-\textbf{t}_I) + \varepsilon(\textbf{y}_k - \textbf{t}_I)$, donc
$$\varphi^{-1} \circ \varPhi(\textbf{y}_k) - \textbf{y}_k = \varphi^{-1} \circ \varPhi(\textbf{t}_I) -\textbf{t}_I + \varepsilon(\textbf{y}_k - \textbf{t}_I) = \varepsilon(\textbf{y}_k - \textbf{t}_I).$$
    
En passant aux normes, et en divisant par $\left\lVert\textbf{y}_k - \textbf{t}_I\right\rVert$, on obtient
$$\frac{\left\lVert\varphi^{-1} \circ \varPhi(\textbf{y}_k) - \textbf{y}_k\right\rVert}{\left\lVert\textbf{y}_k - \textbf{t}_I\right\rVert} = \frac{\left\lVert\varepsilon(\textbf{y}_k - \textbf{t}_I)\right\rVert}{\left\lVert\textbf{y}_k - \textbf{t}_I\right\rVert} \underset{k \to \infty}{\longrightarrow} 0.$$
    
Supposons à présent que pour une infinité de $k \in \mathbb{N}$, on puisse choisir $\textbf{y}_k$ dans $M_k$ mais que $\varphi^{-1}\circ \varPhi(\textbf{y}_k)$ ne soit pas dans $I_k$. Dans ce cas, ces deux points sont à distance au moins $\frac{\mu}{2^k}$ l'un de l'autre, par définition de $\mu$ (distance minimale entre un point de $M$ et un point qui n'est pas dans $P$). Mais alors il existe une sous-suite de points $\textbf{y}_k$ vérifiant
$$\frac{\mu}{c'} = \frac{\mu}{2^k} \frac{2^k}{c'} \leq \frac{\left\lVert\varphi^{-1} \circ \varPhi(\textbf{y}_k) - \textbf{y}_k\right\rVert}{\left\lVert\textbf{y}_k - \textbf{t}_I\right\rVert}.$$
    
La quantité à gauche est constante strictement positive, celle de droite tend vers $0$, contradiction. Par conséquent, à partir d'un certain rang $k_0$, les points $\textbf{y}_k$ vérifient $\varphi^{-1}\circ \varPhi(\textbf{y}_k) \in I_k$, donc $\varPhi(M_k) \subseteq \varphi(I_k)$. En effectuant le même raisonnement pour $\varphi(I_k) \subseteq \varPhi(N_K)$, on a bien montré les inclusions souhaitées.

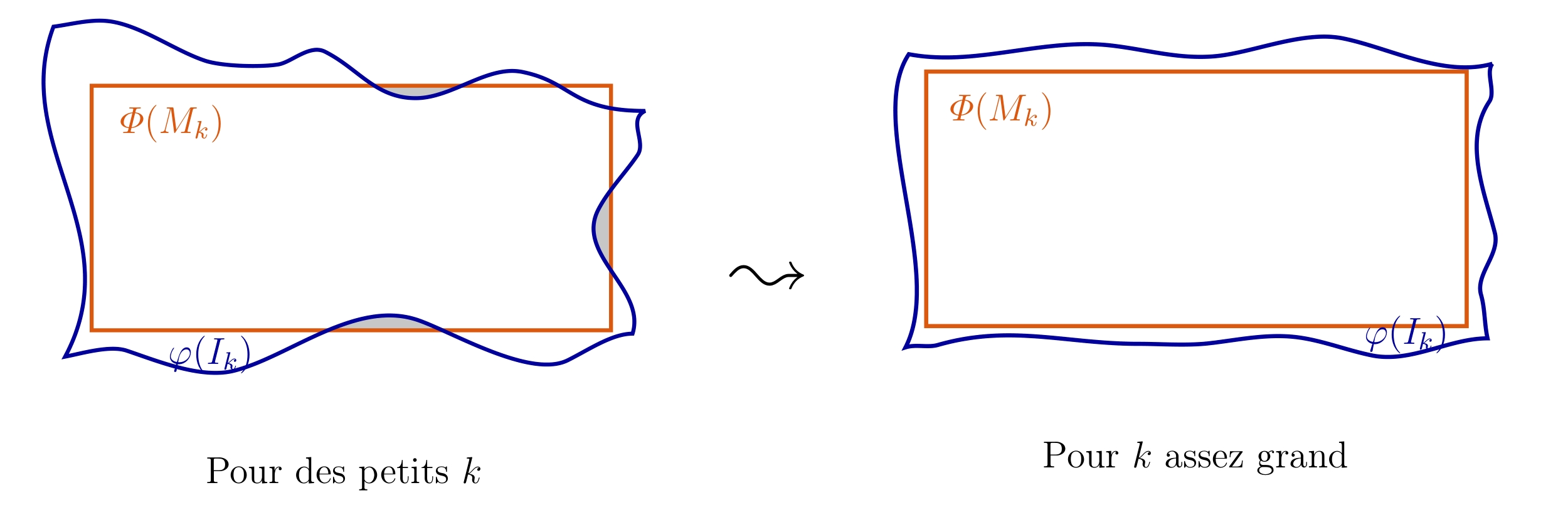
On peut donc comparer leurs volumes : pour tout $k \geq k_0$,
\begin{align*}
   \mathrm{Vol}(\varPhi(M_k)) & = \left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert \mathrm{Vol}(M_k) \\
   & \leq \mathrm{Vol}(\varphi(I_k)) \leq \mathrm{Vol}(\varPhi(N_k)) = \left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert \mathrm{Vol}(N_k).
\end{align*}
En divisant par $\mathrm{Vol}(I_k)$, on obtient
$$\left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert \frac{\mathrm{Vol}(M_k)}{\mathrm{Vol}(I_k)} \leq \mathrm{Vol}(\varphi(I_k)) \leq \frac{\mathrm{Vol}(N_k)}{\mathrm{Vol}(I_k)}, \forall k \geq k_0.$$
En considérant des pavés $M$ et $N$ arbitrairement proches de $P$, les rapports $\frac{\mathrm{Vol}(M_k)}{\mathrm{Vol}(I_k)} = \frac{\mathrm{Vol}(M)}{\mathrm{Vol}(P)}$ et $\frac{\mathrm{Vol}(N_k)}{\mathrm{Vol}(I_k)} = \frac{\mathrm{Vol}(N)}{\mathrm{Vol}(P)}$ peuvent être rendus arbitrairement proches de $1$. On obtient ainsi, par théorème d'encadrement, la convergence du rapport $\frac{\mathrm{Vol}(\varphi(I_k))}{\mathrm{Vol}(I_k)}$ vers $\left\lvert\det(\mathrm{Jac}_{\textbf{t}_I} \varphi)\right\rvert$, concluant la démonstration. $\square$

En recollant tous les morceaux, nous avons démontré le théorème du changement de variables dans $\mathbb{R}^n$. Démonstration qui est valable aussi pour $n = 1$ !

Il est intéressant de remarquer que d'autres preuves ont été données de ce théorème, notamment par Peter Lax dans une série de deux articles 1 et 2 (ses arguments lui permettant de déduire facilement le théorème du point fixe de Brouwer, un résultat qui n'est pas anodin). Les richesses du changement de variables ne manquent pas ! À l'interface entre géométrie, calcul différentiel et topologie, il joue un rôle essentiel dans beaucoup de démonstrations et de calculs pratiques, bien que sa lourdeur et ses petits pièges le rendent souvent mal-aimé.