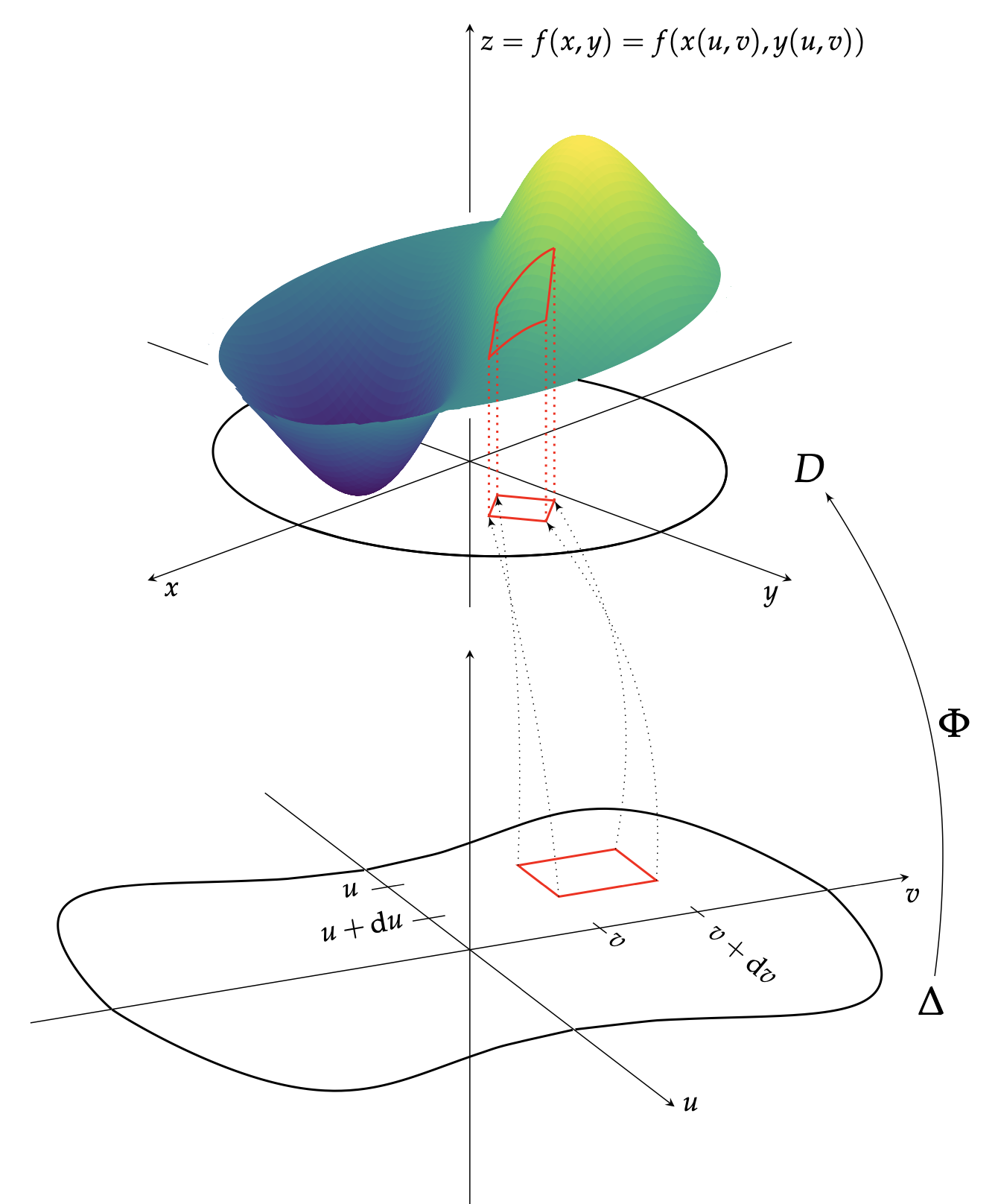
Ce qui fonctionnait avec une variable 1 reste efficace pour deux, à une nuance près comme nous allons le constater. Soit donc à calculer l'intégrale double \begin{equation} \iint_{D} f(x,y)\mathrm{d}x\mathrm{d}y \end{equation} où l'intégrande $f$ dépend du couple $(x,y)$ qui dépend à son tour d'un couple $(u,v)$. Ce dernier lien s'exprime théoriquement par la relation $(x,y)=\Phi(u,v)$ où la fonction $\Phi$ sera parée de toutes les qualités qui, au fil de l'eau, se révéleront utiles. En particulier, $\Phi$ applique un certain domaine $\Delta$ sur le domaine $D$ et s'y différentie à loisir. Par commodité, et malgré la confusion que cela créerait, on identifie volontiers $\Phi$ à ses valeurs. Ainsi trouvera-t-on usuellement \begin{equation} (x,y) = \Phi(u,v)=\left(x(u,v),y(u,v)\right). \label{relation} \end{equation} À mesure que $(u,v)$ balaye $\Delta$ au pas rectangulaire infinitésimal $\mathrm{d}u \mathrm{d}v$, $(x,y)$ progresse en pavant $D$ de dalles élémentaires aux extrémités repérées par

• $\left(x(u,v),y(u;v)\right)$;
• $\left(x(u+\mathrm{d}u,v),y(u+\mathrm{d} u,v)\right) \simeq (x(u,v),y(u,v))+\underbrace{(\frac{\partial x}{\partial u},\frac{\partial y}{\partial u})}_{\frac{\partial \Phi}{\partial u}}\,\mathrm{d}u$;
• $\left(x(u,v+\mathrm{d}v),y(u,v+\mathrm{d} v)\right) \simeq (x(u,v),y(u,v))+\underbrace{(\frac{\partial x}{\partial v},\frac{\partial y}{\partial v})}_{\frac{\partial \Phi}{\partial v}}\,\mathrm{d}v$;
• $\left(x(u+\mathrm{d}u,v+\mathrm{d}v),y(u+\mathrm{d}u,v+\mathrm{d} v)\right) \simeq (x(u,v),y(u,v))+\frac{\partial\Phi}{\partial u}\,\mathrm{d}u + \frac{\partial \Phi}{\partial v}\,\mathrm{d}v.$

La Figure 1 illustre la scène toute entière tandis que la Figure 2 détaille une dalle élémentaire dont les arêtes $\frac{\partial \Phi}{\partial u}\,\mathrm{d}u$ et $\frac{\partial \Phi}{\partial v}\,\mathrm{d}v$ ressortent. Celle-ci, de forme parallélogramme, supporte une pile de hauteur générique $f\left(x(u,v),y(u,v)\right)$. La pile découpe donc une calotte quasi plane sur la surface associée à $f$ et repose sur sa base d'aire $\mathrm{d}\mathcal A$, non pas $\mathrm{d}u\mathrm{d}v$, mais désormais

$$ \mathrm{d}\mathcal A = \mathrm{det}(\frac{\partial\Phi}{\partial u}\mathrm{d}u,\frac{\partial \Phi}{\partial v}\mathrm{d}v) = \begin{vmatrix} \frac{\partial x}{\partial u}\,\mathrm{d}u & \frac{\partial x}{\partial v}\,\mathrm{d}v \\ \frac{\partial y}{\partial u}\,\mathrm{d}u & \frac{\partial y}{\partial v}\,\mathrm{d}v \end{vmatrix} =\underbrace{\begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\ \\ \frac{\partial y}{\partial u}\, & \frac{\partial y}{\partial v} \end{vmatrix}}_{\tfrac{\mathrm{d}(x,y)}{\mathrm{d}(u,v)}}\,\mathrm{d}u\mathrm{d}v. $$

Apparaît le déterminant de la (transposée de) la matrice jacobienne de $\Phi$, c'est-à-dire la jacobienne du changement de variables, souvent notée $\tfrac{\mathrm{d}(x,y)}{\mathrm{d}(u,v)}$ ou $\mathrm{det}(J_\Phi)$ dans la littérature. Le volume algébrique de la pile est ainsi \[ f\left(x(u,v),y(u,v)\right)\tfrac{\mathrm{d}(x,y)}{\mathrm{d}(u,v)}\,\mathrm{d}u\mathrm{d}v. \]

Contrairement aux intégrales simples, les intégrales multiples ne sont pas orientées : $D$ et $\Delta$ sont des domaines géométriques. Seule la cote $f$ est signée. Cela prête à deux conséquences :

• Les aires élémentaires qui interviennent doivent être comptées positivement, et donc le jacobien évalué en valeur absolue ;
• De ce fait, si le pavage revient sur ses pas, les volumes des piles s'accumulent au lieu de se compenser. On exige alors de $\Phi$ d'appliquer bijectivement $\Delta$ sur $D$, éventuellement à quelques détails de mesure nulle près.

Dans ces conditions,
\begin{equation}
\iint_{D} f(x,y)\mathrm{d}x\mathrm{d}y = \iint_{\Delta} f\left(x(u,v),y(u,v)\right)\lvert\tfrac{\mathrm{d}(x,y)}{\mathrm{d}(u,v)}\rvert\,\mathrm{d}u\mathrm{d}v.
\end{equation}

C'est heureux, tout cela s'étend à trois, quatre, voire $n$ variables...