Comment interpréter géométriquement l'équation $a \cos(\theta) - b \sin(\theta) = c$ en mathématiques et comprendre l'interférence entre deux ondes décalées du quart de leur période en sciences physiques ?
En évoquant la transformation d'une somme trigonométrique de la forme $a \cos(\theta) - b \sin(\theta)$ en une quantité du type $R \cos(\theta + \varphi)$, le programme de Terminale STI2D-PCM 1 touche aux mathématiques autant qu'aux sciences physiques.
Dès lors, en mathématiques, on s'intéressera par exemple aux équations d'inconnue $\theta$, \[ a \cos(\theta) - b \sin(\theta) = c. \] Le cas particulier où $c=0$, qui mène directement à $\tan(\theta)=\tfrac{a}{b}$, pourra d'ailleurs justifier a posteriori qu'une tangente inverse participe à la solution générale.
En sciences physiques, dans le domaine « ondes et signaux », on verra que superposer deux impulsions sinusoïdales en quadrature de phase en produit une troisième, simplement déphasée. Aussi la somme de Fourier
\[ \sum_k a_k \cos(k\omega t) - b_k \sin(k \omega t) \] d'un signal périodique se condense-t-elle en cette autre décomposition : \[ \sum_k R_k \cos(k\omega t + \varphi_k). \]
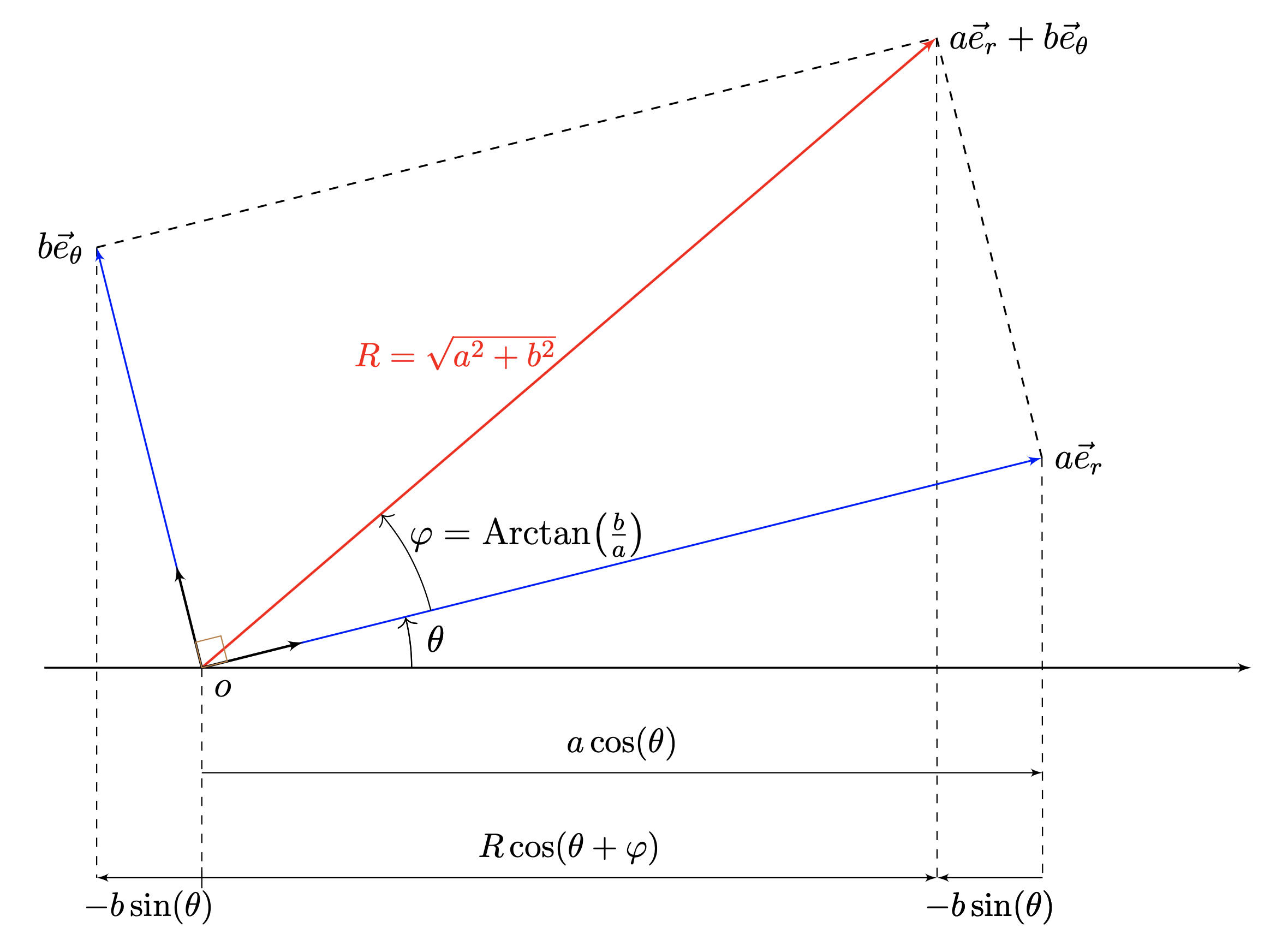
Pour réaliser la transformation voulue de l'expression donnée, on en force classiquement la factorisation par le terme $\sqrt{a^2+b^2}$, puis on traduit les fractions $\tfrac{a}{\sqrt{a^2+b^2}}$ et $\tfrac{b}{\sqrt{a^2+b^2}}$ en tant que lignes trigonométriques d'un même angle. Un tantinet artificielle, l'opération cache des arguments pourtant plus naturels. À la manière de Fresnel2, interprétons plutôt $a \cos(\theta)$ comme le projeté horizontal du vecteur unitaire $\vec{e_r}$ d'angle polaire $\theta$ qu'on aura pondéré du coefficient $a$, et $-b \sin(\theta)$ comme celui de son voisin $\vec{e_\theta}$, d'angle polaire $\theta+\pi/2 = \theta + \frac{2 \pi}{\mathbf 4}$ (d'où la quadrature de phase), qu'on aura pondéré du coefficient $b$. De la sorte, $a \cos(\theta) - b \sin(\theta)$ résulte de la projection horizontale de $a \vec{e_r} + b \vec{e_\theta}$. Le schéma ci-dessous expose cette construction. Sa portée demeure quand bien même l'un des facteurs $a$ ou $b$ ne serait pas positif.
Les dessous de la transformations de l'expression $a \cos(\theta) - b \sin(\theta)$ en l'expression $R \cos(\theta + \varphi)$.
De norme $R = \sqrt{a^2 + b^2}$, le vecteur $a \vec{e_r} + b \vec{e_\theta}$ aura été dévié de l'angle $\varphi = \arctan(\frac{b}{a})$ par rapport au vecteur $a \vec{e_r}$, lequel s'incline de $\theta$ si $a>0$ et de $\theta + \pi$ sinon. Si bien que \[ a\cos(\theta) - b \sin(\theta) = \pm R \cos(\theta+\varphi). \] En électricité, en électromagnétisme, en acoustique, etc. on aura volontiers $\theta = \theta(t) = \omega t$. Il faut donc s'imaginer le repère $(\vec{e_r},\vec{e_\theta})$ tournant à la vitesse angulaire uniforme $\omega$.
Tout ce qui précède s'adapte à l'expression voisine, $a\cos(\theta) + b \sin(\theta)$ en changeant $b$ en $-b$. La branche portée par $\vec{e_\theta}$ s'en trouve réfléchie par rapport à $\vec{e_r}$. Le module $R$ demeure inchangé tandis que $\varphi$ devient son opposé.
