Les formules trigonométriques d'addition peuvent être conçues de manière très naturelle et géométrique, et apparaissent, avec la bonne figure, presque d'un seul coup d'oeil.
Les formules de la trigonométrie classique sont enseignées, à des degrés d'approfondissement divers, dans les classes de Première et Terminale des lycées 1234. Les programmes les y introduisent par l'intermédiaire des nombres complexes et du produit scalaire. Cependant, les premières constructions de $\mathbb{C}$ remontent au XVIe siècle quand le calcul vectoriel ne prit, lui, véritablement son essor qu'au XIXe 5. Les Anciens ne disposaient donc pas de tels outils. Pourtant, les Grecs témoignaient déjà d'une maîtrise avancée de la géométrie du cercle et de celle du triangle. En attestent les travaux de Ptolémée6 au IIe siècle, repris dans l'Antiquité tardive en Inde, traduits et diffusés plus tard par les Arabes avant d'être réimportés en Occident au Moyen-Âge 78. Certes, les énoncés n'avaient pas l'aspect moderne que nous leur connaissons aujourd'hui : à l'époque, on raisonnait sur des cordes sous-tendues par des arcs, plutôt qu'avec des sinus et cosinus, qui n'en sont jamais que les projetés. Mais les propriétés obtenues revenaient strictement au même 9.
Voyons donc comment, avec les moyens élémentaires d'il y a 2000 ans retranscrits dans notre langage, on a pu établir que, par exemple : \begin{equation} \label{eq} \cos(\alpha+\beta) = \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta), \end{equation} ou, tout à fait directement que $$\cos(2 \theta ) = 2\cos^2 (\theta) -1. $$ Féconde, la formule $\eqref{eq}$ détermine ensuite, grâce aux déphasages ad-hoc, les développements de $\cos(\alpha-\beta)$, $\sin(\alpha+\beta)$, $\sin(\alpha-\beta)$ et donc, à l'aide de sommes et différences appropriées, les linéarisation des produits $\cos(\alpha)\cos(\beta)$, $\cos(\alpha)\sin(\beta)$ et $\sin(\alpha)\sin(\beta)$. Soit toute la panoplie des relations d'additions/soustractions, aussi dites de « prosthaphaeresis » : le préfixe, construit sur la « prothèse », signe une augmentation ; le suffixe, construit sur l'« aphérèse » signe une diminution.
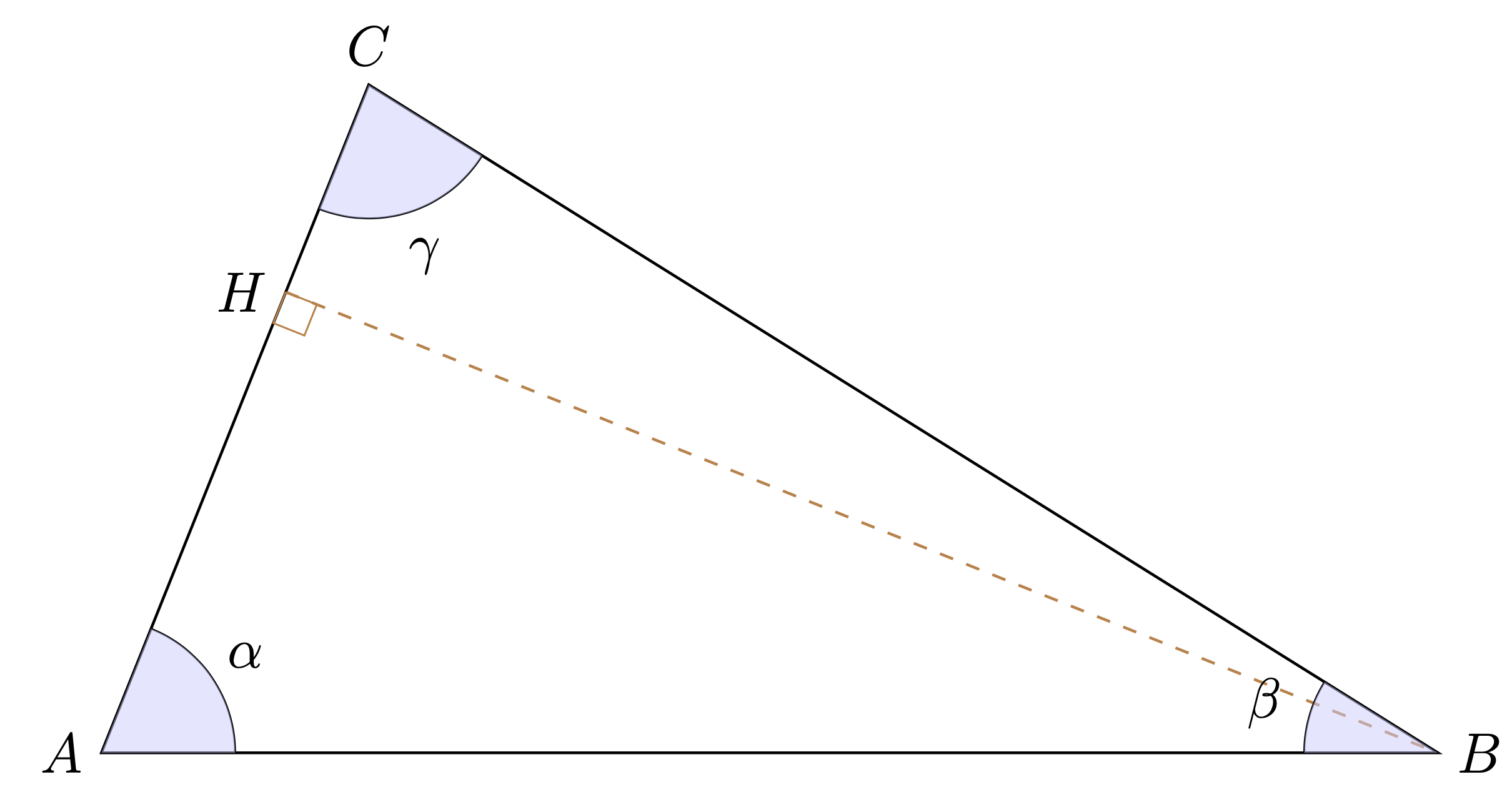
Un premier calcul de $AB^2$ pour obtenir la formule d'Al Kashi.
$ABC$ est un triangle quelconque (acutangle sur la figure précédente, pour simplifier). Soit $H$ le projeté orthogonal de $B$ sur $(AC)$, alors
\begin{align} AB^2 & = AH^2 + HB^2 \tag{théorème de Pythagore} \nonumber \\ & = (\overline{AC} - \overline{HC})^2 +HB^2 \nonumber \\ & = (AC - CB\cos\gamma)^2+(CB\sin \gamma)^2 \tag{orientation telle que $\overline{AC}$>0} \nonumber \\ &= AC^2 + CB^2 (\underbrace{\cos^2\gamma+\sin^2\gamma}_{=1 \text{ (Pythagore)}}) -2 AC.CB\cos\gamma \nonumber \\ &= AC^2 + CB^2 -2 AC.CB\cos\gamma, \label{AlK1} \end{align}
ce qui constitue la formule nommée, a posteriori, en mémoire du mathématicien perse Al Kashi1.
Longueur algébrique (ou orientée, ou encore signée)
Ci-avant, les mesures utilisées sont d'abord algébriques, symbolisées par une barre qui les surmonte ; en effet, le point $H$ aurait pu, en toute généralité, se trouver à l'extérieur du segment $[AC]$. À partir de la 3e ligne de calcul, une fois l'orientation fixée (ici $\overline{AC}>0$), les fonctions trigonométriques prennent les signes à leur charge : par exemple \[ \overline{HC} = CB \cos \gamma \] ou $CB$ est une longueur usuelle (positive !).
Projetons maintenant $C$ sur $(BC)$ et recalculons $AB^2$ :
Un deuxième calcul de $AB^2$ qui, combiné au premier, fournit le développement de $\cos(\alpha+\beta)$.
\begin{align}
AB^2 & = (AK + KB)^2 \nonumber\\
& = \underbrace{AK^2}_{\substack{AC^2 - CK^2 \\ \text{ (Pythagore)}}} +\underbrace{KB^2}_{\substack{BC^2 - CK^2 \\ \text{ (Pythagore)}}} + 2AK.KB \nonumber \\
&= AC^2 + CB^2 - 2 \underbrace{CK.CK}_{AC \sin\alpha\cdot BC \sin\beta} + 2 \underbrace{AK.KB}_{AC \cos\alpha\cdot BC \cos\beta} \label{AlK2}
\end{align}
Soit, en confrontant les deux expressions $\eqref{AlK1}$ et $\eqref{AlK2}$,
\[-\cos\gamma = - \sin\alpha\sin\beta + \cos \alpha \cos \beta.\]
Or $\gamma = \pi - (\alpha + \beta)$, d'où
\[\cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin\alpha\sin\beta.\]
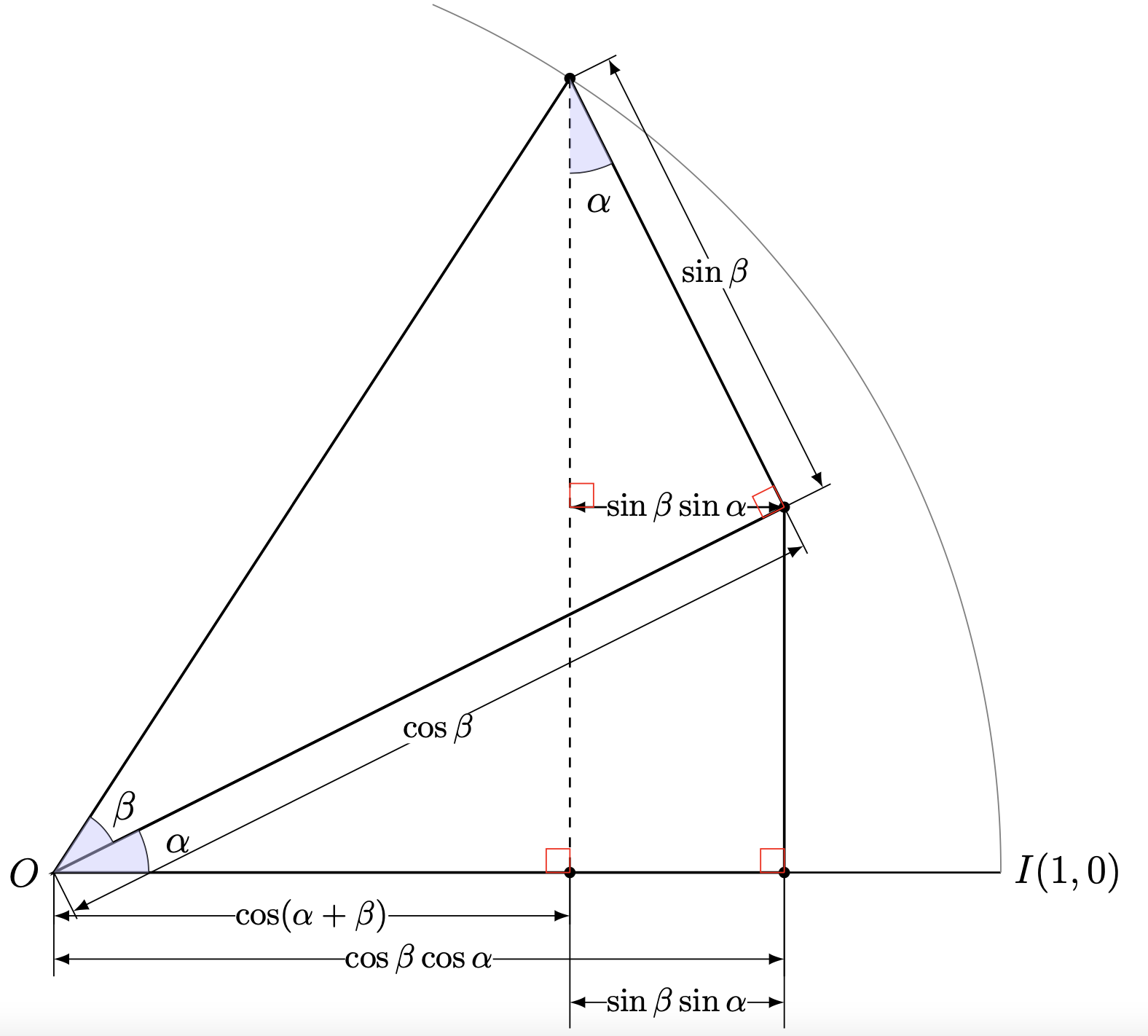
Le point de vue projectif
La deuxième méthode que nous exposons empile astucieusement deux triangles dans le cercle trigonométrique tout en enchaînant les projections 1. Elle figura dans les manuels scolaires français jusque dans les années 1990, avant d'en disparaître assez mystérieusement. En voici l'illustration dans une configuration particulière mais à nouveau générique.
Ainsi, là encore \[\cos(\alpha+\beta) = \cos \alpha \cos \beta - \sin\alpha\sin\beta.\]
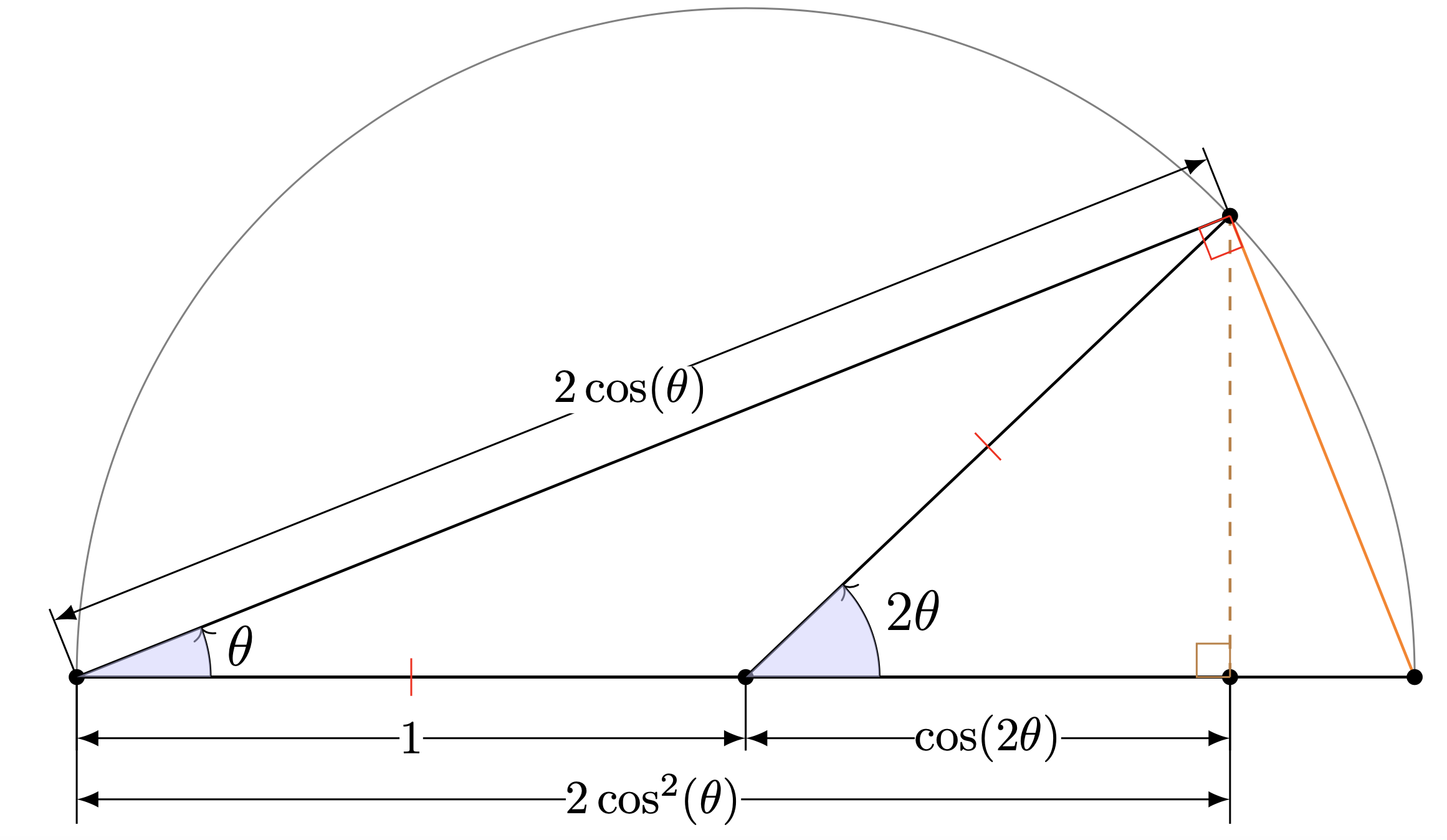
Cas d'école : la formule de duplication
Bien entendu, les formules de duplication et de division découlent des formules d'additions. Mais il y a plus rapide, comme sur ce dessin où l'on inscrit un triangle rectangle dans un demi-cercle unité :
Les formules de déphasage (en opposition ou en quadrature) se déduiraient également des formules d'additions. Mieux, la mise en évidence de quelques axes ou centre de symétrie du cercle trigonométrique nous convaincra immédiatement de ce que
$$\cos\Big(x+\frac{\pi}{2} \Big) = - \sin x $$
ou
$$\cos(x+\pi) = -\cos x. $$