$e^{i\alpha} + e^{i\beta}$ : demi-somme, carton plein !

Formules d'Euler1 et manipulations trigonométriques diverses figurent au programme de mathématiques expertes progTermOption. La factorisation d'une somme de deux nombres complexes unitaires, $e^{i\alpha} + e^{i\beta}$, et donc de $\cos\alpha + \cos\beta$, à l'aide de demi-somme et différence angulaires, s'y prête parfaitement ainsi que l'illustre le schéma ci-après.

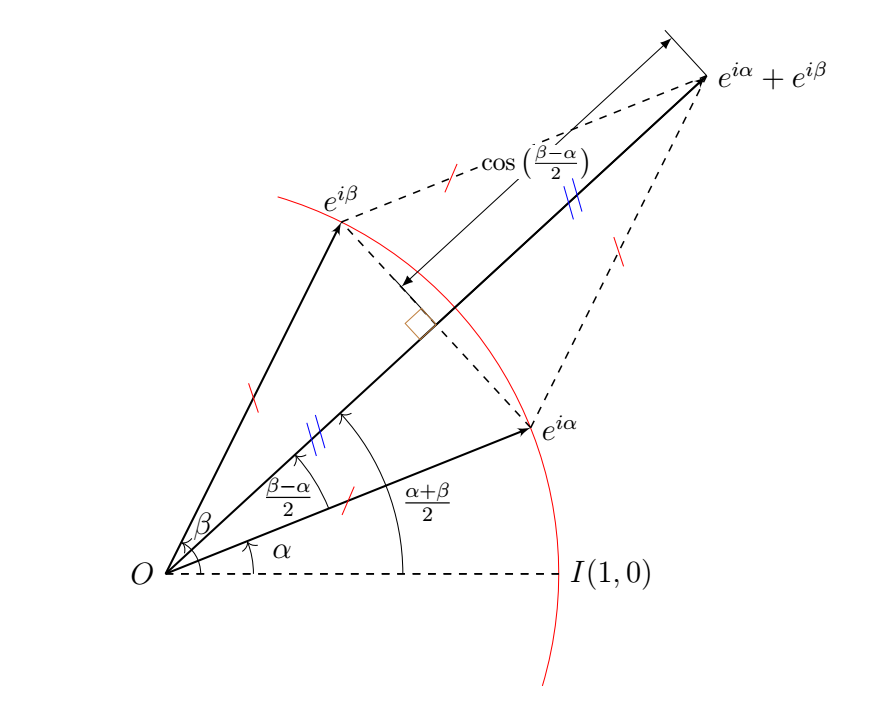
Dans la configuration proposée sur ce graphique, représentative du cas général quand bien même les mesures algébriques y sont positives, on interprète $e^{i\alpha}$ et $e^{i\beta}$ comme affixes de deux côtés d'un losange dont, par symétrie, la diagonale en trait plein est axe bissecteur. Si bien que \[ e^{i \alpha} + e^{i \beta} = 2 \cos\Big(\frac{\beta-\alpha}{2} \Big) e^{i\big(\frac{\alpha+\beta}{2}\big)}. \] En extrayant des deux membres de l'égalité une partie, disons réelle, il vient \[\tag{1}\label{eq} \cos \alpha + \cos \beta = 2 \cos \Big( \frac{\beta-\alpha}{2}\Big) \cos \Big( \frac{\alpha +\beta}{2}\Big). \] Lue de la droite vers la gauche, cette formule a pu permettre au temps de Tycho Brahé2 donc avant l'apparition des tables de logarithmes et selon un procédé qui les préfigure, de multiplier deux nombres réels $x$ et $y$ boyer1968history chabert1994histoire. Réarrangée, (\ref{eq}) donne en effet \[ \cos(p)\cos(q)=\frac{1}{2}\Big(\cos(p+q)+\cos(p-q)\Big). \] Quitte à les recalibrer, en jouant sur des puissances de $10$ afin d'en décaler la virgule, on considérera $x$ et $y$ dans $[-1;1]$. Via une table trigonométrique inverse, on remonte aux arguments $p$ et $q$ satisfaisant $x \simeq \cos p$ et $y \simeq \cos q$. Enfin, par une table trigonométrique directe, on redescend à $\cos(p+q)$, $\cos(p-q)$ et par conséquent $\tfrac{1}{2}\big(\cos(p+q)+\cos(p-q)\big)$, soit à $x\times y$. Le résultat obtenu est d'autant plus précis que les tables utilisées le sont.

Dans un tout autre registre, celui des sciences physiques, la formule (\ref{eq}) sert aujourd'hui encore de base aux techniques de radio transmission, tant analogiques que numériques — on se reportera par exemple à proakis1983comm. Elle explique également le phénomène de battement, ressenti en acoustique lorsqu'on superpose deux pulsations légèrement dissonantes. Ainsi, dans le cadre simplifié où l'on additionnerait deux fondamentales de même amplitude et de même phase3 obtient-on \[\cos(\omega t) + \cos((\omega + \Delta \omega)t) =\underbrace{ 2\cos\Big(\tfrac{\Delta \omega}{2}t\Big)}_{\Large \text{ ①}} \cdot \underbrace{\cos (\omega t +\tfrac{\Delta \omega}{2}t )}_{ \Large \text{ ② }} \]

avec

① : enveloppe basse fréquence dite « modulante »

② : dans laquelle oscille le signal de pulsation quasi $\omega$ dit « porteur ».

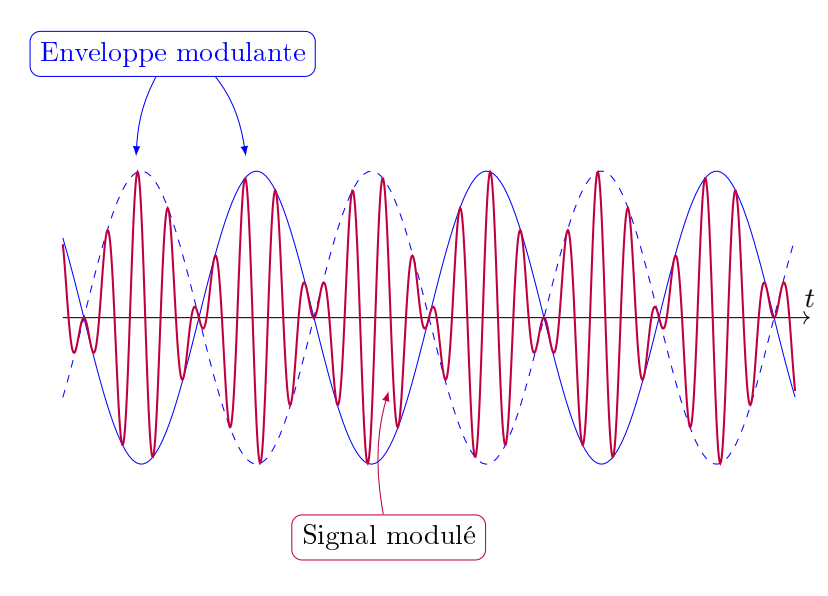
Si les deux fondamentales sont identiques, c'est-à-dire quand $\Delta \omega = 0$, la résultante n'est autre que leur double. Si léger désaccord il y a, mettons d'un hertz soit $\Delta \omega = 2\pi$, le signal produit reste globalement de même nature, mais son volume oscille lentement, à la période $T=\frac{2\pi}{\Delta \omega}$ d'une seconde. Cette période est celle de l'enveloppe, $\left\lvert(\cos\Big(\frac{\Delta \omega}{2}t\Big)\right\rvert$, qui régit l'intensité de l'ensemble. On détecte un léger vibrato, un effet dit de « wawa » ou de « vobulation ». Le programme Python ci-dessous en témoigne. Par défaut, la fréquence de référence y vaut 440 Hz et correspond au $\text{LA}_3$ du diapason, l'enregistrement dure 10 secondes, la cadence d'échantillonnage atteint 8 kHz (d'où une qualité moyenne), et la quantification s'étend sur 16 bits (ce qui n'est pas non plus extraordinaire). Une instruction crée puis fusionne les deux sinusoïdes, ensuite dirigées sur une même voie.

import math
import wave

def Battement(nCanal = 1, nOctet = 2, fEch = 8000,\
        frequence = 440, delta = 5, duree = 10,\
        fichier = 'battement_mono.wav'):
    son = wave.open(fichier,'w')
    nEch = round(duree*fEch)
    parametres = (nCanal,nOctet,fEch,nEch,'NONE','not compressed')
    son.setparams(parametres)
    amplitude = 2**(8*nOctet-2) - 1
    for i in range(0,nEch):
        voie = amplitude*math.cos(2*math.pi*frequence*i/fEch) +\
               amplitude*math.cos(2*math.pi*(frequence+delta)*i/fEch)
        data = wave.struct.pack('h',round(voie))
        son.writeframes(data)
    son.close()

print('Entrer le désaccord (en Hz)')
reponse = input()
Battement(delta = float(reponse))

En voici l'exécutable, traduit en javascript (l'algorithme s'arrête tout seul au bout de 10 secondes ; testez préférentiellement un décalage entre -4 et 4 Hz) :

Une simulation

Tirons maintenant profit de votre équipement stéréo, en générant un son par voie. Cela nécessite quelques aménagements, reportés ci-après.

def Battement(nCanal = 2, nOctet = 2, fEch = 8000,...):
    ...
    amplitude = 2**(8*nOctet-1) - 1
    for i in range(0,nEch):
        voie1 = amplitude*math.cos(2.0*math.pi*frequence*i/fEch)
        voie2 = \
            amplitude*math.cos(2.0*math.pi*(frequence+delta)*i/fEch)
        data = wave.struct.pack('hh',round(voie1),round(voie2))
        son.writeframes(data)
    son.close()
    ...
    ...

L'idée peut sembler séduisante... mais testez-la ! Avec un casque, cela ne fonctionne pas ; et sans, ce n'est audible qu'en rapprochant les enceintes tout en vous en distançant assez. La faute au cerveau, qui ne mélange pas arithmétiquement ce qu'il reçoit de vos deux oreilles.

Concluons sur l'accordage d'un instrument par la méthode du battement. Dans un orchestre, les musiciens jouent leur LA en même temps. Si, de loin (cf. supra), le chef n'entend pas le sifflement d'un « wawa » désagréable, c'est bon signe... Et de près ? Avec un instrument solo comme la guitare ? Pour en régler les cordes les unes relativement aux autres, on pince l'une à vide, et simultanément sa voisine, la main gauche posée sur la frette qui produit la même note. Et ainsi de suite, par exemple du MI aigu (la chanterelle) au MI grave. Mais s'ajoutent quelques difficultés, disons, artistiques. La guitare est un instrument polyphonique très coloré (par sympathie, plusieurs cordes résonnent en harmonie quand on en excite une), et qui ne tient pas les sons (ils s'affaiblissent très vite, contrairement au violon que l'archet entretient). À résumer les expériences tentées par les auteurs, musiciens amateurs, disons que pour entendre quelque chose, on préférera un modèle électrique à la tenue plus longue. Sur un modèle classique, nous n'avons rien perçu de probant à l'écoute... ou notre ouïe est-elle mal pas exercée ? Par contre, en cas de battement, la vibration du manche, amplifiée par la caisse, est palpable et très nette au toucher.