Ces questions, tout un chacun se les pose un jour ou l'autre au moment de signer chez son banquier. Sans rien céder à la rigueur, mais en empruntant aux univers de la biologie et de l'informatique, nous verrons en quoi les nouveaux programmes de lycée en rendent les réponses accessibles dès la classe de première.
Loin d’être naïves, mais au contraire stimulantes et imaginatives, les mathématiques qui sous-tendent notre propos ouvriront un champ fascinant, fait d’un matériau riche et exploitable dans le cadre du « grand oral » de terminale. Les candidats aux CAPES de mathématiques ou de sciences économiques et sociales pourront également y trouver des éléments utiles à leur préparation :
- Programme du CAPES externe de mathématiques, session 2020.
- Programme du CAPES externe de sciences économiques et sociales, épreuve de l’entretien à partir d’un dossier, session 2020.
Un effort que récompense le plaisir de comprendre et d’aller plus loin, et que les clés de votre future auto ou de votre prochain appartement méritent sans doute bien.
Vous pouvez aussi retrouver cet article sur le site SES-ENS où il a été publié conjointement. Une bonne occasion de montrer les ponts entre SES et mathématiques !
Introduction
Donner aux élèves quelques clés de lecture en matière d’éducation économique et budgétaire est un enjeu national. Les programmes, à travers plusieurs domaines du socle, le soulignent1 tandis qu’un plan pluriannuel et interministériel adopté en 2013 l’avait, du reste, déjà pointé2, donnant lieu à la production de ressources pédagogiques pour le collège3. Le sujet soulève cependant trois difficultés au moins. Un obstacle est technique, eu égard aux concepts mathématiques mobilisés. Un autre est cognitif : à quel âge les élèves sont-ils réceptifs au sujet ? Un troisième est philosophique, ou même moral, toujours latent quand il s’agit d’argent4.
C’est sur les opérations de crédit que nous avons choisi de nous pencher. Au croisement de plusieurs disciplines enseignées au lycée et jusqu’aux BTS : économie et comptabilité notamment5, elles sollicitent aussi des mathématiques bien balisées par les programmes, qu’elles illustrent donc à merveille. La proportionnalité et la notion de pourcentage sont présentées dès le collège6, ces chapitres étant consolidés en classe de seconde à travers les taux d’évolution. Les suites arithmétiques et géométriques apparaissent en spécialité de 1ère générale, et figurent dans toutes les classes de la voie technologique. Leur étude est approfondie dans l’option complémentaire de terminale, tandis que les logarithmes y sont introduits. Une initiation à l’analyse numérique et à la programmation jalonne, quant-à elle, tous les cycles. Les outils étant disponibles, il restait à les mettre en œuvre.
Qu’est-ce qu’un crédit ?
Le principe
« Je vous paierai, lui dit-elle, avant l’août, foi d’animal, intérêt et principal ». En glissant ces quelques vers dans une célèbre fable, Jean de La Fontaine7 nous rappelle combien souscrire un crédit est un acte qui engage. Par contrat, la cigale s’oblige à rembourser, en différé et selon des règles précises, la fourmi dont elle est redevable de lui avoir prêté un certain capital $C$. Cet échange de services permet à l’emprunteur (appelé aussi débiteur), qui est un particulier, une entreprise voire un État, d’acheter sans attendre une voiture, de réaliser des travaux, d’acquérir un bien immobilier, de résorber un découvert, d’ouvrir un commerce, de financer un projet, de construire un pont, etc. Le prêteur (appelé aussi créancier) peut être un interlocuteur unique comme une banque — on parle alors d’emprunt indivis. Il arrive parfois qu’il se compose d’une multitude de porteurs, selon le système des obligations.
Sauf aléa, le prêteur recouvre sa mise in fine. S’y ajoute un intérêt $I$ pour le dédommager de s’être privé temporairement et à ses risques d’une richesse : c’est le prix de l’abstinence et de la confiance et là est le retour sur investissement. La manière dont sont évalués et étalés les intérêts dépend de la nature du crédit, de sa durée, du profil de l’emprunteur et de contingences macroéconomiques.
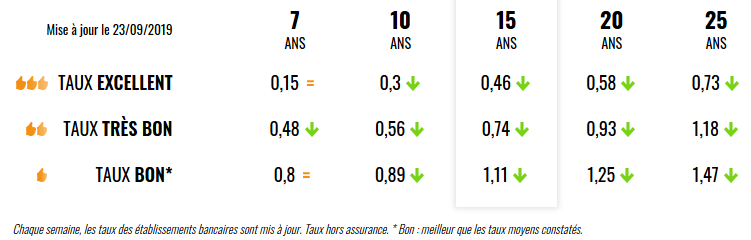
Certes les mentalités évoluent, et les circuits de microcrédit formalisant des pratiques traditionnelles comme la tontine se développent8. Selon les adages populaires, on négocie toutefois plus volontiers avec un ménage « riche » et « en bonne santé » ; à court terme – un « tiens vaut mieux que deux tu l’auras » ; dans le contexte stable d’une inflation modérée où la monnaie se déprécie peu. Dans la pratique bancaire, ces éléments guident le choix d’un taux nominal $\tau$ (figure 1) lequel gouverne des intérêts périodiques dont le cumul constitue l’intérêt total $I$.
« Time is money » dit-on ? Que l’argent travaille ne va pas forcément de soi et soulève d’inévitables questions morales. Déjà le philosophe Aristote9 condamnait l’usure. La charia musulmane puis l’Église se joignirent un peu plus tard à ses avertissements : « recevoir un intérêt pour l’usage de l’argent prêté », disait Saint Thomas d’Aquin10, « est de soi injuste car c’est faire payer ce qui n’existe pas ». Si le débat subsiste, vif, l’informatique ayant dématérialisé des transactions qui semblaient déjà virtuelles, le recours au crédit est aujourd’hui universel, autorisé, strictement encadré par la loi. Devenu familier, il recèle cependant quelques subtilités mathématiques qui sont d’autant plus satisfaisantes à expliquer qu’elles convoquent avec intelligence les programmes de lycée.
Taux, intérêts simples, intérêts composés
Le taux d’intérêt $\tau$ désigne un pourcentage que le créancier applique à son débiteur au gré d’un certain échéancier (décliné, selon, en jours, mois ou années) et sur une certaine assiette (un capital servant de base de calcul). Il en découle un intérêt qui vient alourdir potentiellement et périodiquement la dette de l’emprunteur.
Voici deux cas d’école. Certes édulcorés, ils demeurent représentatifs tant des mécanismes en jeu que de leurs ordres de grandeur.
Agios. Quand un compte est à découvert, la banque estime qu’elle fait crédit. Dans les limites d’un certain plafond, elle définit un taux (par défaut) et le rapporte a posteriori au solde (négatif) de son détenteur jusqu’à retour à l’équilibre. On parle d’intérêts simples : la dette peut bien se creuser de nouveaux intérêts, la quantité « taxée », elle, n’en dépend pas.
Exemple. Soit un découvert de $C= 1\,000 €$ le dimanche, au taux journalier $\tau= 0,1\%$. Un scenario vraisemblable serait le suivant...
| Lundi |
|
| Mardi |
|
| Mercredi |
|
| Jeudi |
|
| Un trimestre plus tard |
|
Prêt à la consommation.
Dans ce cadre, après étude du dossier, la banque accorde un taux et le rapporte à la dette du client au fur et à mesure que cette dernière varie. Les intérêts font donc boule de neige, on dit qu'ils se composent.
Exemple. Financement d'une voiture achetée $C =10\thinspace 000\, €$ pour Noël ; taux mensuel $\tau= 1\% ;$ mensualités fixes de $400\,€.$ Chaque mois le client rembourse une part du capital emprunté (amortissement) et paie un intérêt qui s'applique au montant de la dette en cours. Déroulons les événements dans ce qui préfigure un tableau d'amortissement (voir le paragraphe "Tableau d'amortissement : une application numérique")...
| Janvier |
|
| Février |
|
| Mars |
|
| Etc. |
|
Les calculs pas à pas sont ici pénibles. Nous pourrions les automatiser à l'aide de l'ordinateur. Pour autant nous ne saurions prédire avec exactitude leur fin. Patience, les sections Démontrer la « formule des banquiers », une preuve par « capitalisation » et Démontrer la « formule des banquiers », une preuve par « actualisation », permettront tout cela.
Les intérêts simples ne présentant pas de difficulté majeure, nous resserrerons désormais la discussion sur les seuls intérêts composés.
Interprétation démographique du crédit à intérêts composés. Équation aux différences, schéma fonctionnel
Avant tout formalisme mathématique, décrivons le phénomène étudié en osant un parallèle. Dans la logique des intérêts composés, l'argent « fait des petits ». Assimilons donc la dette $C$ à une population (de bactéries, par exemple) qui se reproduit périodiquement au taux de natalité associé $\tau$ et dont toutes les générations (nouvelles, plus anciennes, pionnières) sont immédiatement et éternellement fertiles1. Les échéances s'apparentent alors à des prélèvements au sein de la colonie, venant contrecarrer, et idéalement inverser sa croissance. Leur rythme est synchrone au cycle des naissances. Leur ampleur peut a priori fluctuer.
Notons $D_0=C, D_1, D_2, D_3,\ldots$ les dettes successives (tant que le crédit n'est pas intégralement remboursé). Appelons $e_1, e_2, e_3,\ldots$ les échéances (pas nécessairement fixes, on les qualifie alors de modulables) et $i_1, i_2, i_3,\ldots$ les intérêts produits à chaque période. En filant la métaphore, les dettes $D_k$ correspondent aux quantités de bactéries restantes, les $i_k$ aux naissances, les $e_k$ aux disparitions.
Au démarrage,
\begin{equation}
D_0=C
\end{equation}
Au fil de l'eau, s'installe l'équation d'évolution où $k\geq1$
\begin{equation}
D_k=(1+\tau) D_{k-1}-e_k \label{relationRecurrente}
\end{equation}
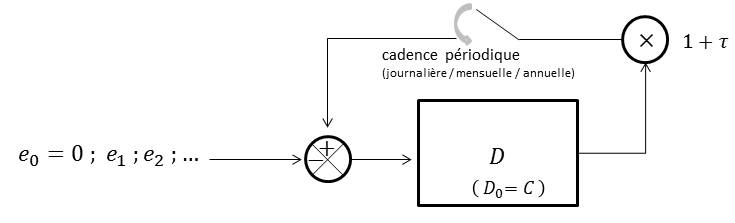
Ainsi la variable dette $D$, initialisée à $C$, subit-elle une rétroaction (les naissances) diminuée d'une action extérieure (les disparitions), ce que symbolise le schéma fonctionnel de la figure suivante.
Une fois incarné, le problème devient palpable et dynamique, et l'analogie inspirera encore davantage les paragraphes subséquents. Intriquer les sciences du vivant aux mathématiques n'est pas, en soi, une idée neuve. Elle tient d'une longue tradition ; référence à Fibonacci1 observant ses lapins d'élevage, à Lotka-Volterra2 modélisant proies et prédateurs, ou à Malthus3 croisant économie et démographie.
Capital dû, taux, annuité, durée : quelle dépendance ?
La relation récurrente (\ref{relationRecurrente}) fournit les informations utiles de proche en proche. Mais, sauf à exécuter les calculs à la queue leu leu, elle n'annonce pas d'emblée la durée du remboursement, soit le nombre $N$ d'échéances nécessaires. Dans le cas d'échéances fixes4 où $e_k=e$ pour tout $k\geq1$, il est pourtant possible de rassembler les paramètres du crédit et donc de tout prévoir dans une expression récapitulative, la « formule des banquiers » :
\begin{equation}
e=\frac{C\tau}{(1-(1+\tau)^{-N} )} \label{formuleBanquiers}
\end{equation}
Ensuite, et fonction des besoins, libre à chacun de lire cette équation de gauche à droite, de droite à gauche, ou, par des tours de passe-passe algébriques, de la retourner telle une crêpe. Par exemple on pourrait fixer $C$, $N$ et $e$ et tirer5 $\tau$ de l'équation polynomiale
$$
(1+\tau)^N (C\tau-e) + e = 0
$$
Souvent présentée comme une « recette magique » par ses propres usagers (prêteurs et emprunteurs), et pour toute esthétique qu'elle soit, (\ref{formuleBanquiers}) n'a rien de miraculeuse. Nous allons l'établir par deux méthodes — en « capitalisant » ou en « actualisant » l'argent prêté, et nous l'appliquerons dans le paragraphe Tableau d'amortissement : une application numérique puis dans la section plus technique Avec des mathématiques plus expertes... à un exemple numérique assisté du tableur. Le propos y sera illustré avec un crédit immobilier dont nous supposerons connus le capital $C$ (disons $C =100\,000 € $), le taux annuel (disons $\tau= 1\%$), la durée en nombre $N$ d'années (disons $N=10$). Hypothèses simplificatrices, les échéances, constantes, seront réglées annuellement — on parle alors d'annuités $a$ (jouant ici le rôle de $e$) bien que, concrètement, l'usage veuille les convertir en mensualités lesquelles pourraient de surcroît se moduler.
Le lecteur pressé sautera directement à la section Tableau d'amortissement : une application numérique pour une mise en œuvre pratique. Le lecteur curieux et plus patient reprendra, papier et crayon en main, les étapes démontrant la fameuse formule (\ref{formuleBanquiers}) « des banquiers » exposées dans les sections Démontrer la « formule des banquiers », une preuve par « capitalisation » et Démontrer la « formule des banquiers », une preuve par « actualisation » : les deux approches proposées font aussi l'originalité de cet article.
Cette méthode est tournée vers l'avenir. Elle donne une valeur au temps à travers le taux d'intérêt par lequel, à chaque période, le capital s'étoffe. Chronologiquement, on aurait tendance à aller de l'avant, en emboîtant les relations6 (\ref{relationRecurrente}) les unes dans les autres.
Une première substitution entraîne
$$
D_1 = (1+\tau) D_0 - a = (1+\tau)C-a
$$
Puis une seconde,
$$
D_2=(1+\tau) D_1-a=(1+\tau)\left((1+\tau)C-a\right)-a
=(1+\tau)^2 C-a\left((1+\tau)+1\right)
$$
Une troisième,
$$
D_3=(1+\tau) D_2-a=(1+\tau)^3 C-a\left((1+\tau)^2+(1+\tau)+1\right)
$$
Et, plus généralement,
\begin{equation}
D_k=(1+\tau)^k C-a\left((1+\tau)^{k-1}+\cdots+(1+\tau)+1\right)
\end{equation}
Il y aurait moyen d'en découdre puisqu'affleurent des lois géométriques, sauf qu'on ne cerne pas très bien les objets manipulés. Rouvrons plutôt notre boîte de Petri7. À chaque période on ponctionne la quantité $a$ de bactéries, quand naît la quantité $D_k \tau$. Pour qu'il y ait extinction, il faut d'ores et déjà
\begin{equation}
\underbrace{C \tau}_{1\text{er descendants}} \leq \underbrace{a}_{\text{prélèvement}} \label{condition}
\end{equation}
... sans quoi le processus dérive : la culture prospère indéfiniment. Sous la condition (\ref{condition}) que nous assumerons, elle entre par contre dans une spirale dégressive. S'il y a moins de bactéries, il y a encore moins de descendants. Et puisqu'on en retire toujours autant, cela continue à décroître.
À chaque itération, les bactéries prélevées sont quelconques : elles peuvent être choisies aléatoirement car, jeunes ou âgées, elles sont également fécondes. En revanche, même s'ils tendront vers le même but, les calculs emprunteront des chemins différents.
Dans l'approche par « capitalisation » le remboursement du crédit commence par supprimer systématiquement tous les nouveaux nés (la dette fraîchement créée) à chaque échéance. On puise l'effectif complémentaire, de sorte que le total soit porté à $a$, parmi les cellules souches (le capital). Le tribut que paient ces dernières est l'amortissement $m$, étymologiquement une « mise à mort ». Avec les conventions ci-avant, nous poserons $m_1=a-C\tau$, $m_2=a-D_1 \tau$. Tant que la colonie n'est pas éradiquée, la relation qui suit s'applique :
\begin{equation}
\underbrace{a}_{\text{annuité (prélèvement)}} =\underbrace{ D_{k-1} \tau}_{\substack{\text{intérêts annuels}\\\text{(retrait de tous les nouveaux-nés)}}} + \underbrace{m_k}_{\substack{\text{amortissement annuel}\\ \text{(mort de cellules souches)}}} \label{formuleAnnuite}
\end{equation}
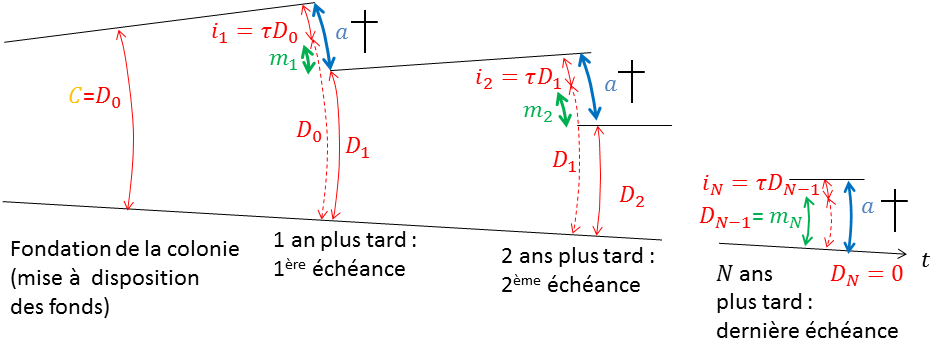
La figure suivante résume sur une frise les nombreuses notations rencontrées.
Les amortissements $ m_1, m_2, m_3\ldots$ semblent croître. Mieux, ils progressent géométriquement. En effet, via (\ref{relationRecurrente}), $ D_k \tau=(1+\tau) D_{k-1} \tau-a\tau$. Donc par (\ref{formuleAnnuite}),
$$
a-m_{k+1}=(1+\tau)(a-m_k )-a\tau
$$
qui mène à
\begin{equation}
m_{k+1}=(1+\tau) m_k \label{relationdAmortissement}
\end{equation}
Initialement, $ m_1=a-\tau D_0=a-\tau C$. Il vient donc grâce à (\ref{relationdAmortissement}) puis (\ref{formuleAnnuite})
$$
m_{k+1} = (1+\tau)^k m_1 = (1+\tau)^k (a-\tau C)
$$
et
$$
D_k=\frac{1}{\tau} (a-m_{k+1} )=\frac{1}{\tau} \left(a-(1+\tau)^k (a-\tau C)\right)
$$
Or, tout à la fin, $D_N=0$. D'où
\begin{equation}
a=(1+\tau)^N (a-\tau C)
\end{equation}
Les membres où $a$ figurent une fois regroupés, nous renouons avec (\ref{formuleBanquiers}) qui est désormais prouvée.
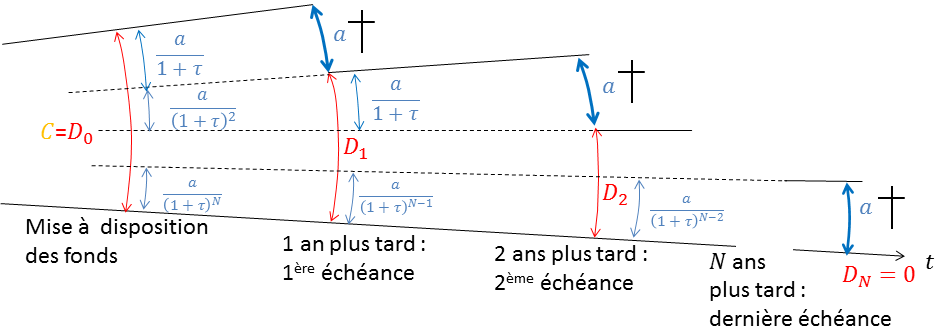
Réciproque de la précédente et tout à fait équivalente sur le plan mathématique, la démarche consiste à tout rapporter au présent, à savoir l'origine de l'emprunt, considéré comme l'état « actuel ». Repensons aux bactéries. Par la seule force de l'esprit, imaginons maintenant que les individus périodiquement extraits soient ceux d'une même famille, issue de la même lignée dont on coupe toute la branche (la fraction de capital augmenté des dettes qu'il a directement ou indirectement enfantées, à tous les degrés donc). Remontons sa généalogie. La quantité $a$ puisée l'année $n$ provient d'un groupe de taille $\frac{a}{1+\tau}$ l'année $n-1$, lui-même fruit d'un groupe de taille $\frac{a}{(1+\tau)^2}$ l'année $n-2,\dots,$ jusqu'à remonter à la source, un effectif de $\frac{a}{(1+\tau)^n}$ « pionniers ». Après $n$ années, il ne reste plus personne et la racine, correspondant à $C$, est neutralisée. D'une incroyable efficacité, cet artifice synthétisé dans la figure qui suit conduit directement à
\begin{equation}
C=\frac{a}{(1+\tau)}+\frac{a}{(1+\tau)^2} +\cdots+\frac{a}{(1+\tau)^N} \label{formuleBanquiersV2}
\end{equation}
Après sommation géométrique1, nous retrouvons bien (\ref{formuleBanquiers}) dans une version revisitée :
\begin{equation}
C=\frac{a}{\tau} (1-(1+\tau)^{-N} ) \label{formuleBanquiersV3}
\end{equation}
Donnons donc $C =100\thinspace000 € $, $\tau= 1\%$ et $N=10$ années. La formule (\ref{formuleBanquiers}) ou ses équivalents (\ref{formuleBanquiersV2}) et (\ref{formuleBanquiersV3}) imposent une annuité $a =10\thinspace558,20 € $ au centime près arrondi par défaut. Sur $N =10$ années, le client aura acquitté la somme $Na$ et le crédit lui sera revenu à $Na-C$, respectivement $105\, 582 €$ et $ 5\, 582 €.$
Un tableau d'amortissement dresse, au cours du temps, l'état de plusieurs variables :
- la dette $D=(D_k )_k$, aussi appelée « capital restant dû ». Elle correspond à la somme que récupérerait la banque en cas de remboursement anticipé du crédit ;
- l'intérêt annuel $i=(i_k)_k$. Selon la législation ad hoc, il est parfois possible de le déduire fiscalement ;
- l'amortissement annuel $m=(m_k)_k$.
On y adjoint parfois deux colonnes :
- l'intérêt cumulé $I=(I_k)_k$, où $$I_k=i_1+i_2+⋯+i_k=\sum\limits_{p=1}^k i_p$$
- l'amortissement cumulé $M=(M_k)_k$, où $$M_k=\sum\limits_{p=1}^k m_p $$
Au terme des $N$ échéances, $I_N$ indique le coût final du crédit tandis que la dette s'annule et l'argent avancé est restitué : $D_N=0$ et $M_N=C$. Le calcul de $a$ effectué, on transfère sur tableur les formules reliant les cellules $D_1$, $D_0$ (initialisée à $100\,000$) et $i_1$ ; $I_1$, $I_0$ (initialisée à 0) et $i_1$ ; $m_1 $ et $i_1$ ; $M_1$, $M_0$ (initialisée à 0) et $m_1$. On les étend en faisant glisser la poignée de recopie. En voici les instructions puis le déroulé, conforme à la théorie aux arrondis près. Les intérêts s'amenuisent. Parallèlement la dette s'efface petit à petit.
| année | D | i | I | m | M |
| 0 | 100 000 | 0 | 0 | ||
| 1 | $=(1+0,01)D_0-10 558,2$ | $=0,01*D_0$ | $=I_0+i_1$ | $=10 558-i_1$ | $=M_0+m_1$ |
| 2 | 80 788,01 | 904,41 | 1 904,41 | 9 653,78 | 19 211,98 |
| 3 | 71 037,69 | 807,88 | 2 712,29 | 9 750,31 | 28 962,30 |
| 4 | 61 189,87 | 710,37 | 3 422,67 | 9 847,82 | 38 810,12 |
| 5 | 51 243,57 | 611,89 | 4 034,57 | 9 946,30 | 48 756,42 |
| 6 | 41 197,80 | 512,43 | 4 547,00 | 10 045,76 | 58 802,19 |
| 7 | 31 051,58 | 411,97 | 4 958,98 | 10 146,22 | 68 948,41 |
| 8 | 20 803,90 | 310,51 | 5 269,50 | 10 247,68 | 79 196,09 |
| 9 | 10 453,74 | 208,03 | 5 477,54 | 10 350,16 | 89 546,25 |
| 10 | 0,08 | 104,53 | 5 582,08 | 10 453,66 | 99 999,91 |
Nous développons ici plusieurs points laissés en friche. Les alinéas (4.1) et (4.2) sont indépendants du suivant.
En pratique, les banques ramènent les taux d'intérêt annuels à des taux mensuels. Sauf exception1, elles le font au prorata temporis, en remplaçant l'annuité au taux $\tau$ par douze mensualités consécutives au taux $\tau'$ douze fois moindre, $\tau'=\frac{\tau}{12}$. Mutatis mutandis, l'échéance annuelle devient une échéance mensuelle $m'$, avec
\begin{equation}
m'=\frac{\tau C}{12(1-(1+\frac{\tau}{12})^{-12N})} \label{echeanceMensuelle}
\end{equation}
Les douze mensualités concourent à l'annuité $a'=12m'$, qui diffère légèrement de l'expression2 (\ref{formuleBanquiers}). Pour comparaison, le quotient $\frac{a}{a'}$ est à l'unité ce que le quotient
$$
\frac{(1+\frac{\tau}{12})^{12N}}{(1+\tau)^N}
$$
est, lui aussi, à l'unité, ou encore ce que le quotient
$$
\frac{(1+\frac{\tau}{12})^{12}}{(1+\tau)}
$$
est, en définitif, à l'unité. Or ce quotient est plus grand que 1, conséquence de la formule du binôme de Newton3. Nous retiendrons que fractionner les remboursements en mensualités donne un (léger) avantage au client. Sur notre exemple, $m' =876,04$, $a' =10\, 512,49$ soit un gain d'une quarantaine d'euros annuels. Le prêteur récompense ainsi le retour avancé du capital.
Un conseiller financier commence par jauger la capacité de remboursement de son client. C'est elle qui dicte $a'$, ou $m'$, qui ne doit pas excéder le tiers des revenus disponibles afin d'éviter tout surendettement. On ajuste ensuite le nombre $12N$ de mensualités... et l'on révise peut-être aussi le budget. À la ligne (\ref{echeanceMensuelle}), l'inconnue n'est donc plus $m'$, mais $N$. Pour un meilleur confort, transformons (\ref{echeanceMensuelle}) en
$$
(1+\tau')^{-12N}=1-\frac{\tau C}{12m'}
$$
Cette équation n'a pas toujours de solution $N$ entière. La contrainte est relaxée en remplaçant $N$ par une variable temporelle continue $T$ exprimée en année. Derechef,
$$
(1+\tau')^{-12T}=1-\frac{\tau' C}{m'}
$$
Puis
$$
T=-\frac{1}{12} \frac{ \ln(1-\frac{\tau'C}{m'})}{\ln(1+\tau')}
$$
Par exemple, avec un ménage gagnant $2\,500 €$ par mois, les mensualités peuvent aller jusqu'à $m' =833$. Pour $C = 100\,000€ $, on obtient $T =10,54$ soit un crédit sur un peu plus de 126 mois : (presque) exactement 126 mois et 15 jours. Les premiers 126 mois s'enchaînent normalement. Le résidu peut être calculé au prorata. De ce fait, en admettant qu'un mois compte 31 jours, il s'élèverait à $(1+\tau'\times\frac{15}{31}) D'_{126}$.
Le remboursement par annuités constantes est très répandu en France au point d'être considéré comme la norme selon le grand public. D'autres modalités existent cependant.
Annuités en progression arithmétique. Jusqu'ici l'amortissement $m=(m_k )_k$ allait croissant. Cette tendance serait contrebalancée en réduisant symétriquement les échéances $a=(a_k )_k$. D'ici à rechercher un dosage qui stabiliserait $m$\ldots Pour ce faire, ré-écrivons la relation (\ref{formuleAnnuite}) sous sa forme plus générale
$$
a_k=D_{k-1} \tau+m_k
$$
Déclinée au rang suivant, nous tirons également
$$
a_{k+1}=D_k \tau+m_{k+1}
$$
Notre intention d'avoir $m_{k+1}=m_k$ (rebaptisé $m$, identifié pour l'occasion à la suite constante) implique, en soustrayant les deux équations précédentes
$$
a_{k+1}-a_k=\underbrace{(D_k-D_{k-1})}_{-m_k=-m} \tau
$$
Comme $\sum\limits_{k=1}^N \underbrace{m_k}_{=m\!\!\!\!} =C$, précisons que $m=\frac{C}{N}$.
Les annuités suivent une progression arithmétique de raison (négative) $- C\frac{\tau}{N}$ et de premier terme $a_1=D_0 \tau+m_1=C(\tau+\frac{1}{N})$. Par quel sortilège un phénomène foncièrement géométrique — les intérêts composés — a-t-il pu engendrer une réponse arithmétique ? C'est d'un ravissement divin dont les mathématiques nous font le si joli cadeau.
Annuités en progression géométrique. Tout augmente, c'est bien connu : les prix mais aussi (prétend-on) les revenus. De là à indexer les annuités au taux $\pi$ d'inflation anticipé... L'effort à consentir suit la progression géométrique $a_k= a_1 (1+\pi)^{k-1}$. En adaptant la formule (\ref{formuleBanquiersV2}) à cette préoccupation supplémentaire, nous obtenons
\begin{equation}
C=\frac{a_1}{1+\tau}+\frac{a_1 (1+\pi)}{(1+\tau)^2} +\cdots+\frac{a_1 (1+\pi)^{N-1}}{(1+\tau)^N}
\end{equation}
Puis
$$
C=\frac{a_1}{1+\pi} \thinspace \thinspace \frac{1-(\frac{1+\pi}{1+\tau})^N}{1-(\frac{1+\pi}{1+\tau})}
$$
Et moyennant $\pi \neq\tau$,
\begin{equation}
C=\frac{a_1}{(1+\tau)^N } \thinspace \thinspace\frac{1+\tau}{1+\pi} \thinspace \thinspace \frac{(1+\tau)^N-(1+\pi)^N}{\tau-\pi}
\end{equation}
On remarque en $\tau-\pi$ le taux d'intérêt réel $\tau_{\text{réel}}$. Effectivement, quand un euro en devient $1+\tau$ mais qu'un bonbon qui en coûtait un en coûte ensuite $1+\pi$, l'euro d'origine, amplifié puis affaibli dans la foulée, n'équivaut plus qu'à $\frac{1+\tau}{1+\pi}$ bonbons. À toutes sucreries égales, le pouvoir d'achat n'est plus dilaté que de $\frac{1+\tau}{1+\pi}$, ratio égal à $1+\tau_{\text{réel}}$ selon la définition de l'économiste Fisher4. C'est un peu comme si nos bactéries se multipliaient dans un volume (la boîte) qui, lui aussi, augmentait. La concentration suit, mais au ralenti. Et tant que $\tau$ et $\pi$ sont petits, on a au premier ordre
\begin{eqnarray*}
\frac{1+\tau}{1+\pi} \simeq (1+\tau)(1-\pi) &=& 1 + \tau - \pi - \tau \pi \\
&\simeq& 1 + \tau - \pi
\end{eqnarray*}
D'où en bonne approximation, ainsi qu'il a été dit,
$$
\tau-\pi=\tau_{\text{réel}}
$$
Quand le taux d'inflation n'a pas été anticipé ou qu'il a été sous-estimé, le taux d'intérêt réel s'en trouve réduit. Cela peut avoir pour conséquence de rendre solvable un ménage qui ne l'était pas ou plus, en ramenant le niveau de son remboursement sous la barre des 33% de ses revenus. Ou lui permettre d'augmenter ses mensualités tout en diminuant la maturité du crédit sans perdre de son pouvoir d'achat.
Les rouages du crédit à peine dévoilés, de nouvelles questions émergent. Pour plus de réalisme, il faut maintenant complexifier le modèle et y agréger d'autres flux. Tenir compte des frais de dossier et des assurances. Intégrer la fiscalité. Élaborer des montages : prêt relai, investissement locatif, achat sur plan aux intérêts intercalaires, location avec option d'achat, etc. La presse, une riche bibliographie ainsi qu'une abondante sitographie, dont [5-8, 10-12,17] donnent un éventail, viendront en aide à celui qui souhaite approfondir tous ces points.
Mais l'importance de cette invitation à l'économie est peut-être ailleurs. Derrière chaque événement important de la vie, souvent heureux, parfois moins : achat immobilier, succession, mariage, divorce, naissance, etc., on trouve des sciences sociales dont il n'est pas inutile de cerner les principes et de chiffrer les montants qu'elles engagent. Y être vigilant aide, une fois l'âge adulte, à tenir la barre. Là est aussi l'enjeu pour nos élèves.
Remerciements
Les auteurs remercient Anne Châteauneuf-Malclès, de l'ENS Lyon, Stéphan Sémirat, de l'Université Grenoble Alpes, ainsi que le groupe d'auteurs CM-ENS Ulm de CultureMath.
Références
[1] Arrêté du 29 avril 2019, référentiel du BTS Comptabilité et Gestion.
[2] BO no 17 du 23 avril 2015, Socle commun de connaissances, de compétences et de culture.
[3] BO spécial du 22 janvier 2019, Programmes d’enseignement du lycée général et technologique.
[4] BO no 30 du 26 juillet 2018, Programmes d’enseignement du cycle 4.
[5] Xavier Caruso, « Petites leçons sur le calcul des intérêts bancaires », Images des mathématiques, CNRS, consulté en octobre 2019.
[6] Claude Danthony, « Emprunts : mensualités, intérêts, taux, TEG, risques de taux », Images des mathématiques, CNRS, consulté en octobre 2019.
[7] Jean-Guy Degos et Jean-Yves Degos, Comprendre les mathématiques financières, Ellipse, 2013.
[8] Éric Favro, Mathématiques financières, Dunod, 1991.
[9] Site pédagogique sur la monnaie et la finance La Finance Pour Tous. Consulté en octobre 2019.
[10] Le Particulier, magazine d’actualité juridique, patrimoniale, et pratique. [11] Le Revenu, magazine de conseil en bourse et placements.
[12] Le Figaro, quotidien d’actualité économique et financière.
[13] Maria Nowak, On ne prête (pas) qu’aux riches, JC Lattès, 2005.
[14] Plan pluriannuel contre la pauvreté et pour l’inclusion sociale adopté lors du Comité interministériel de lutte contre les exclusions, 2013.
[15] Programme du CAPES externe de mathématiques, session 2020.
[16] Programme du CAPES externe de sciences économiques et sociales, épreuve de l’entretien à partir d’un dossier, session 2020.
[17] Didier Schlacther, Premiers pas en mathématiques financières, Hachette, 2012.