B z z zz zzz zzzzz zzzzzzzz zzzzzzzzzzzzz zzzzzzzzzzzzzzzzzzzzz ...
On a coutume d’introduire la suite de Fibonacci1 en dénombrant une population de lapins dont chaque couple, adulte au bout d'un mois, engendre à son tour une fratrie de deux lapereaux tous les mois, eux-mêmes futurs parents, et cetera, figure 1. Cependant, ce modèle théorique ne met pas toujours très à l’aise. Un autre scénario fait gravir à une grenouille un escalier par volées d'une ou deux marches, figure 2. Toutefois, le contexte est légèrement surfait. Sans renoncer à la métaphore animale, abordons le sujet sous l'angle de la « vie amoureuse » des abeilles. Voilà de quoi piquer notre curiosité... et découvrir un univers captivant, qui résonne avec les programmes de première : en mathématiques 23 comme en sciences de la vie et de la Terre 4.
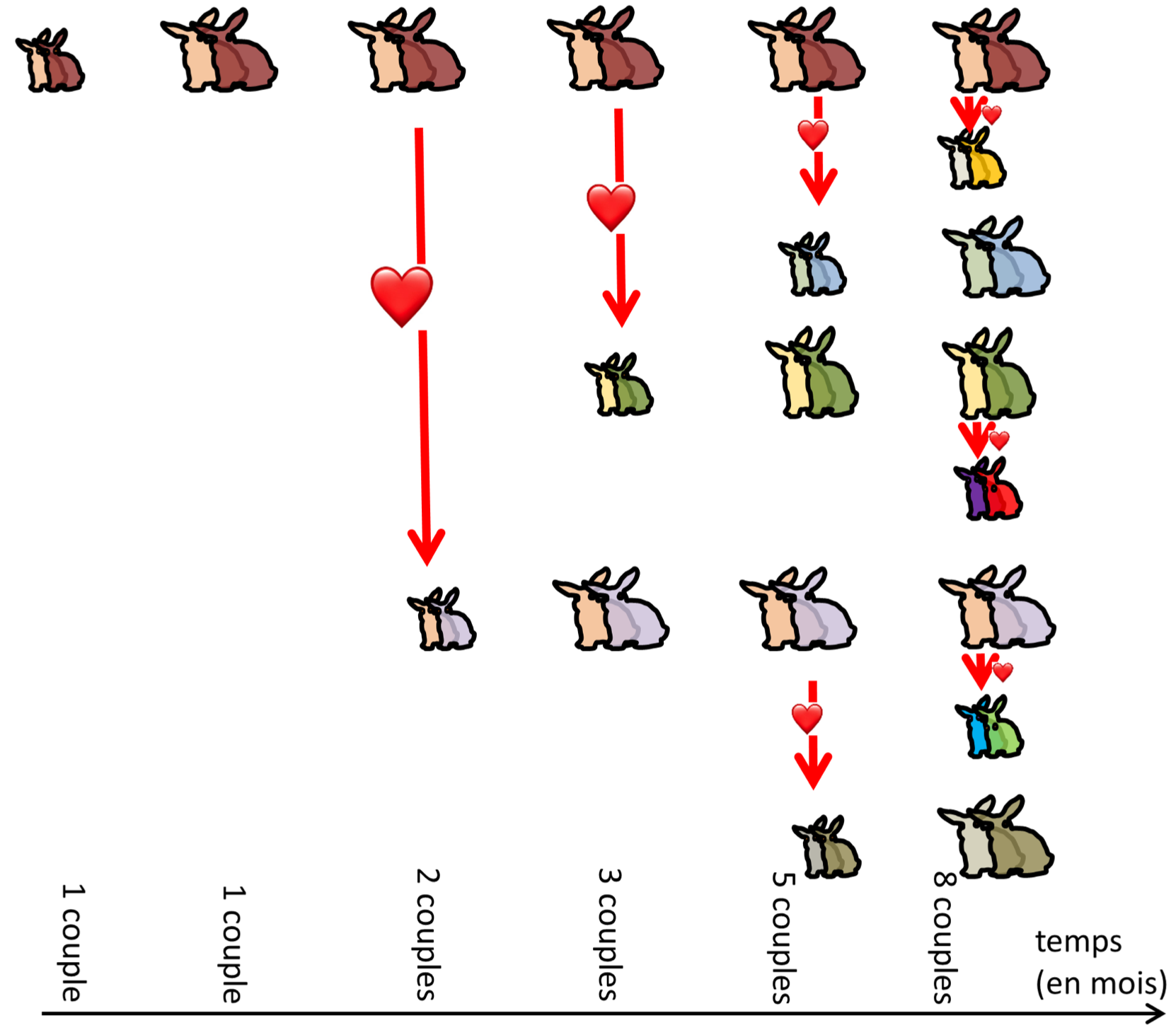
Chaque couple de lapins donne naissance à un couple de lapereaux un mois plus tard lequel, une fois à la maturité d'adulte, c'est-à-dire encore un mois plus tard, donne à son tour naissance à un couple de lapereaux. La famille s'agrandit ; on prouverait que le total de ses membres, cumulé jusqu'à la génération de degré $n$, est le nombre $F_n$ de Fibonacci 5. Sur le schéma, une ligne représente un couple donné, mois après mois.
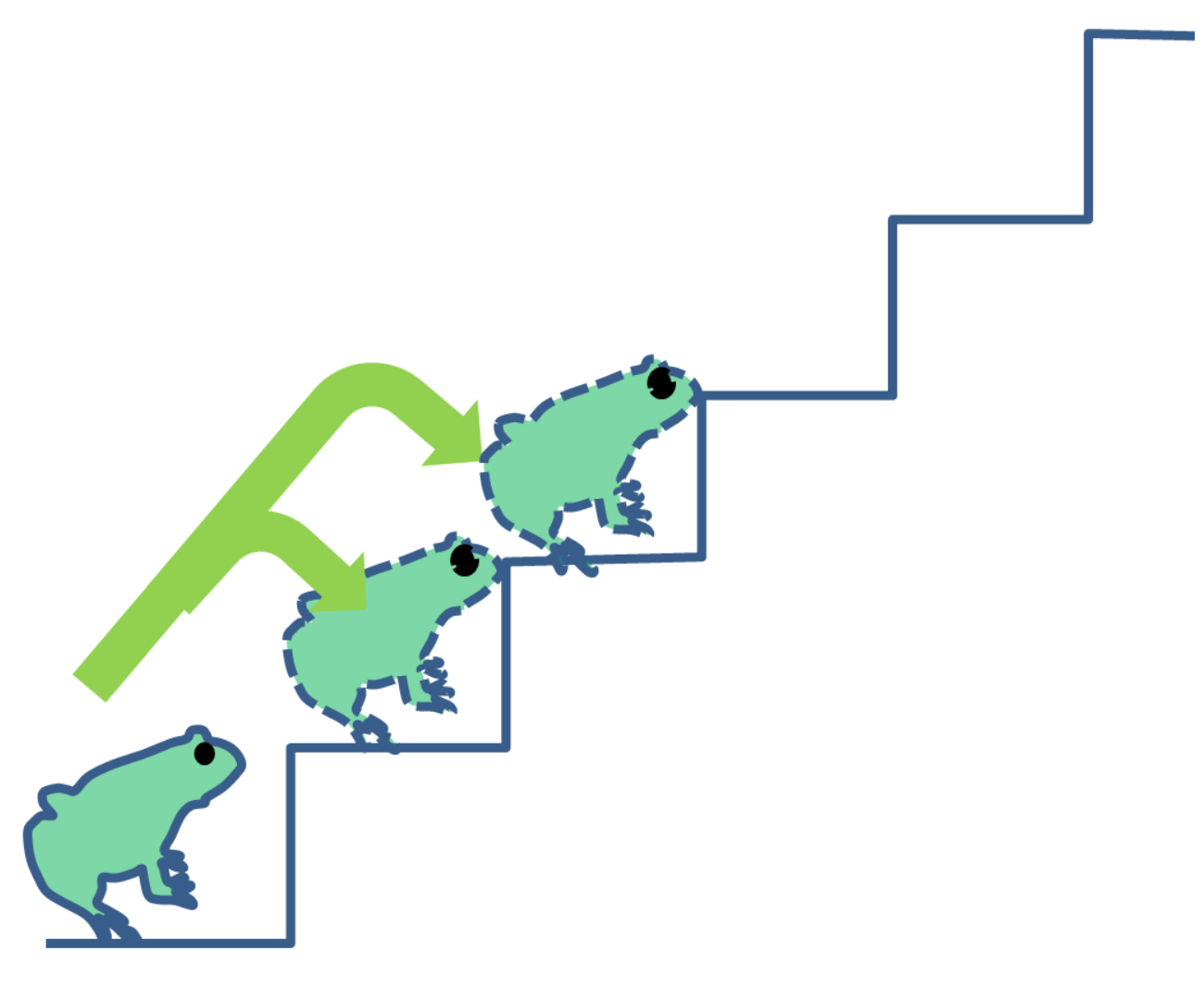
La grenouille peut faire des sauts d'une ou deux marches. On prouverait que le nombre de façons qui s'offre à elle pour atteindre le haut de la $n$e marche vaut $F_n$ 6
Préliminaires
Une ruche abrite une reine, des abeilles mâles (les faux bourdons) ainsi que des abeilles femelles ordinaires (qui sont stériles, sauf en période de régence), très majoritaires. La reine peut vivre plusieurs années, ses sujets quelques semaines seulement. Il faut donc les renouveler. C'est pour cela que la reine pond en continu une centaine d'œufs par jour.
Les abeilles relèvent du genre Apis. Il existe bien des « vrais » bourdons (ou tout simplement, bourdons), mais ils sont d'un genre différent : le genre Bombus. Bourdons et abeilles appartiennent à la même famille — les Apidae, du même ordre — les Hyménoptères, de la même classe — les Insectes, du même groupe — les Arthropodes, d'un même ensemble — les « Invertébrés », terme aujourd'hui désuet.
Dans sa jeunesse, la reine abeille accomplit un vol nuptial : grande lune de miel durant laquelle elle récolte, une fois pour toutes, les gamètes d'une dizaine de faux bourdons. Elle conserve leurs semences dans une poche, sorte de banque de sperme : la spermathèque. Puis, tout au long de sa vie, une fois partie fonder ou reprendre une colonie, elle en fera usage en la comprimant ou non pour en extraire ou pas le contenu : c’est une particularité de la reproduction des abeilles et plus généralement des Hyménoptères (abeilles, bourdons, guêpes, frelons, fourmis, etc.).
Quand elle féconde un œuf avec un spermatozoïde pris dans sa spermathèque, la reine fait naître une abeille femelle. L'abeille femelle pourra occuper différents postes dans son existence : ménagère, ouvrière, gardienne, ventileuse, butineuse, etc. Quelques-unes, biberonnées à la gelée royale plus longtemps que leurs camarades, règneront à leur tour.
Quand elle ne féconde pas un œuf avec un spermatozoïde, la reine fait naître une abeille mâle (un faux bourdon). La boucle se boucle : ce dernier partira vers son vol nuptial. Il y rencontrera (peut-être) une princesse d'une colonie voisine et mourra quelques minutes après l'accouplement puisqu'il y perd une portion de son abdomen.
L'origine de la fécondation des œufs n'est ni déterministe ni parfaitement élucidée. Mais une corrélation entre la taille des alvéoles dans lesquelles pond la reine, et la naissance de femelles ou de mâles, est observée. Des facteurs environnementaux semblent également jouer leur rôle.
Laissons-nous aller à quelques interprétations susceptibles de traduire certains avantages de ces mécanismes de régulation à l'échelle de la ruche.
Pourrait-on envisager que la taille réduite d'une alvéole, lieu de ponte, comprime l'abdomen et donc la spermathèque de la reine ? Au point de favoriser le passage de la semence mâle à la croisée des œufs encore vierges, et de les féconder... Cela promettrait plus de naissances femelles. Donc à terme plus d'abeilles ouvrières, et par là des alvéoles mieux construites, mieux nettoyées, plus spacieuses, synonymes d'un meilleur développement de la colonie.
Et lors de la belle saison, que supposer d'une moindre contraction de la spermathèque, alors plus dilatée ou moins sollicitée, sous l'effet de températures désormais plus élevées ou de molécules printanières (phéromones par exemple) plus abondantes ? Cela promettrait un surcroît de naissances mâles : c'est de circonstance au moment le plus propice d'essaimer.
Bref, une abeille femelle possède un « papa » et une « maman » ; une abeille mâle (le faux bourdon) n'a qu'une « maman ». De ce fait, son caryotype possède deux fois moins de chromosomes : le faux bourdon est haploïde alors que les femelles y compris la reine sont diploïdes, à la différence de l'être humain où les deux sexes sont diploïdes. Chez les abeilles d'une même colonie, les femelles sont toutes sœurs ou demi-sœurs et les mâles tous frères détenteurs d'un unique « matrimoine ». Ce lien familial très fort contribue probablement à la cohésion du groupe.
Si, les abeilles comptent !
Venons-en aux mathématiques. Nous souhaitons remonter l'arbre généalogique d’un faux bourdon — appelons-le Willy 7 — et compter ses ancêtres de degré $n$. Notons $A_n$ leur nombre. Si Willy était un homme, on aurait $A_n = 2^n$ puisque chaque nœud découle de deux branches. Mais c'est une abeille mâle.
Réfléchissons. D'abord, $A_0 = 1$. Notre ami Willy a une « maman » et c’est tout, soit $A_1 = 1$. Sa « maman » a une « maman » (la grand-mère) et un « papa » (le grand-père), soit $A_2 = 2$, etc. Au rang $n$, tout le monde a une « maman » ; et les femelles, qui sont au même nombre que les individus d’ordre $n-1$, ont aussi un « papa », figure 3. Donc, pour tout entier $n\geq 1$, $$ A_{n+1} =A_n + A_{n-1}. $$ Nous reconnaissons la relation de Fibonacci assortie de ses traditionnelles conditions à l'origine. D'où la conclusion, valable pour tout entier naturel $n$, $$ A_n = F_n. $$
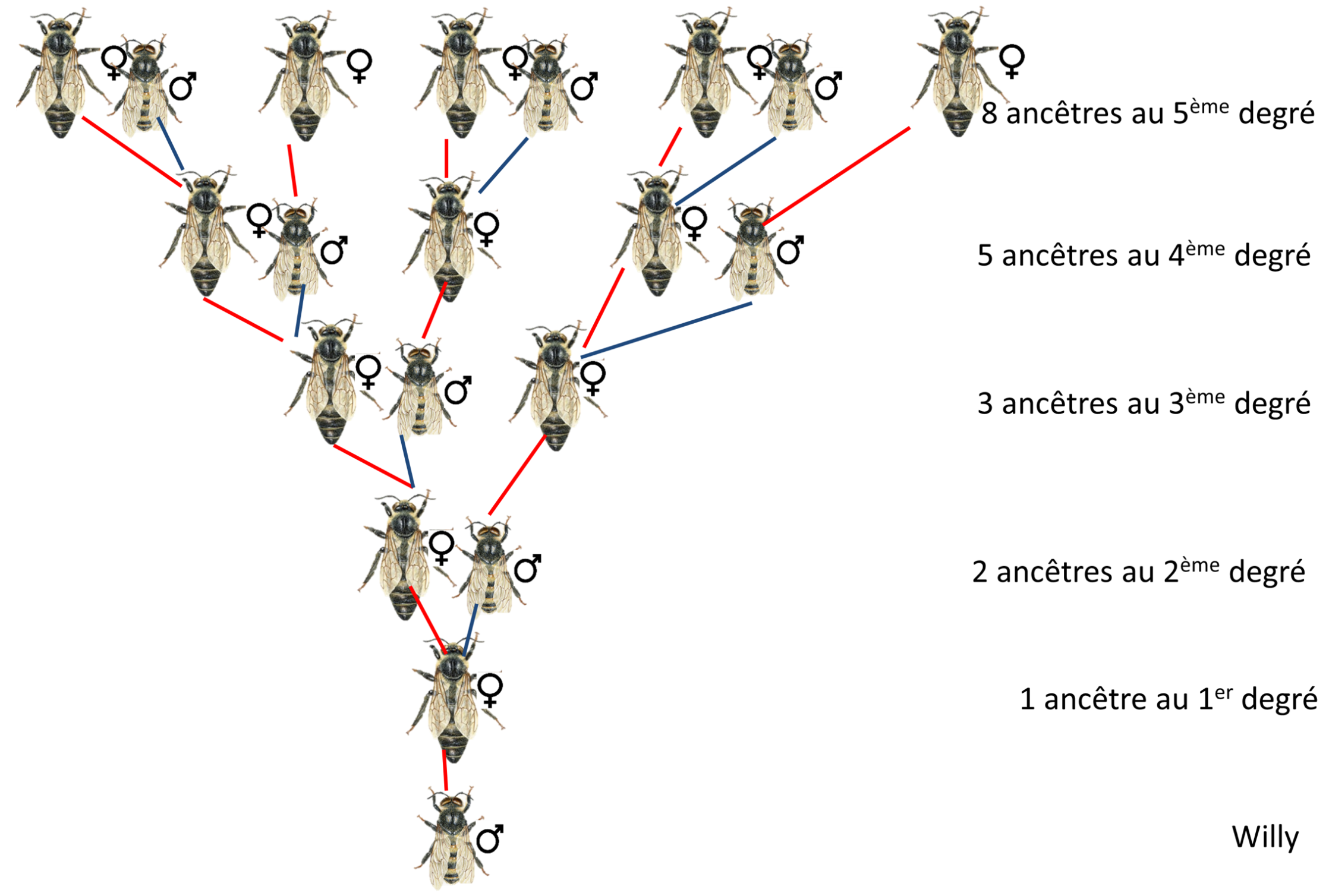
Un trait rouge remonte à une génitrice (reine abeille), un trait bleu à un géniteur (faux bourdon). Haploïde, le faux bourdon est conçu par parthénogénèse (la racine grecque parthenos renvoie à la virginité car l'œuf n'est pas fécondé)
Cette histoire d'abeilles n'est pas si « bébête ». Le sujet peut même rapidement s'envoler : en considérant par exemple le morphisme « alphabétique » $\varphi$ qui remplace, dans tout mot composé des lettres8 $A$ et $B$, la lettre $A$ par le digramme $AB$ et la lettre $B$ par la lettre $A$. Par exemple, $\varphi(AABA)=ABABAAB$. Auquel cas, $F_n$ compte le nombre de lettres constituant $\varphi^n(B)$, image de $B$ par $n$ itérés successifs de $\varphi$ avec $n\in\mathbb{N}$ et la convention $\varphi^0 = \text{id}$.







