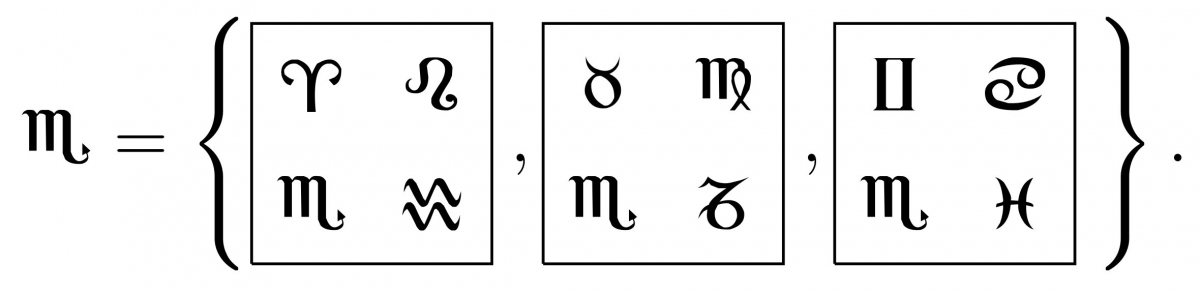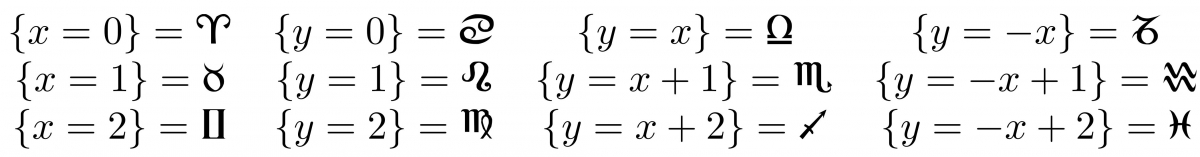La géométrie d'incidence est ce qui reste de la géométrie quand on oublie les distances, les angles... et qu'on ne se concentre plus que sur les questions d'appartenance d'un point à une droite, de parallélisme, etc.
Discipline à cheval entre la géométrie axiomatique et la combinatoire, elle comporte encore aujourd'hui des problèmes ouverts fondamentaux. Cet article présente ce qui est peut-être l'objet le plus basique en géométrie d'incidence : les plans (affines) finis, sur lesquels beaucoup reste encore à apprendre1.
La géométrie, même plane, parle de points et de droites, mais pas uniquement. Les notions de distance et d'angle, par exemple, sont au cœur des théorèmes les plus classiques de géométrie.
A contrario, la géométrie d'incidence (plane) ne garde de la géométrie que deux objets : les points et les droites et la relation d'incidence qui les unit : un point peut être ou ne pas être sur une droite. Cela permet de redéfinir certaines notions géométriques comme le parallélisme (deux droites sont parallèles si elles sont égales ou si aucun point n'est sur les deux simultanément) et l'alignement (trois points sont alignés s'ils sont sur une même droite) mais il est impossible d'exprimer par exemple le théorème de Pythagore dans ce formalisme.
Dans cet article, on se propose de considérer la notion de plan en géométrie d'incidence. On verra notamment que ce point de vue permet de poser des questions intéressantes de combinatoire. On rencontrera au passage une énigme due à Euler ou Dobble, un jeu de société.
Structures d'incidence
Définition
Une structure d'incidence est un couple $(\Omega, \Delta)$, où $\Delta \subset \mathcal P(\Omega)$.
On utilisera souvent un vocabulaire géométrique : les éléments de $\Omega$ seront des points, ceux de $\Delta$ des droites. Si $A \in \Delta$ et $\delta \in \Delta$ sont tels que $A\in \delta$, on dira, au choix, que le point $A$ est sur la droite $\delta$, que $\delta$ passe par $A$, que $A$ et $\delta$ sont incidents, etc.
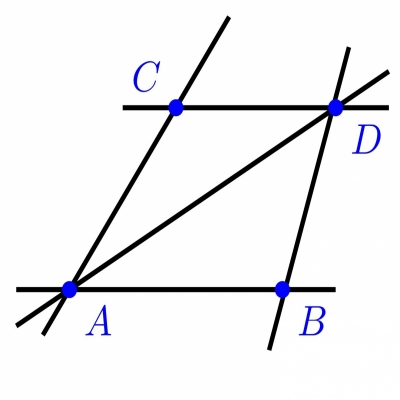
Exemple usuel : L'exemple à garder en tête est celui qui motive notre vocabulaire, celui où $\Omega$ est formé des points du plan (ordinaire) et où $\Delta$ est l'ensemble des droites du plan.
On pourra utiliser dans tous les exemples qui suivent les notions usuelles de parallélisme ($\delta \mathbin{\!/\mkern-5mu/\!} \delta'$ si $\delta = \delta'$ ou $\delta \cap \delta' = \varnothing$) et d'alignement ($A$, $B$ et $C$ sont alignés si $\exists \delta \in \Delta : A, B, C \in \delta$). À nous de voir au cas par cas si cela est très pertinent.
La notion de structure d'incidence est très malléable. L'exemple suivant, un peu ridicule, montre qu'elle contient des exemples qui sont très différents du modèle que l'on vient d'évoquer.
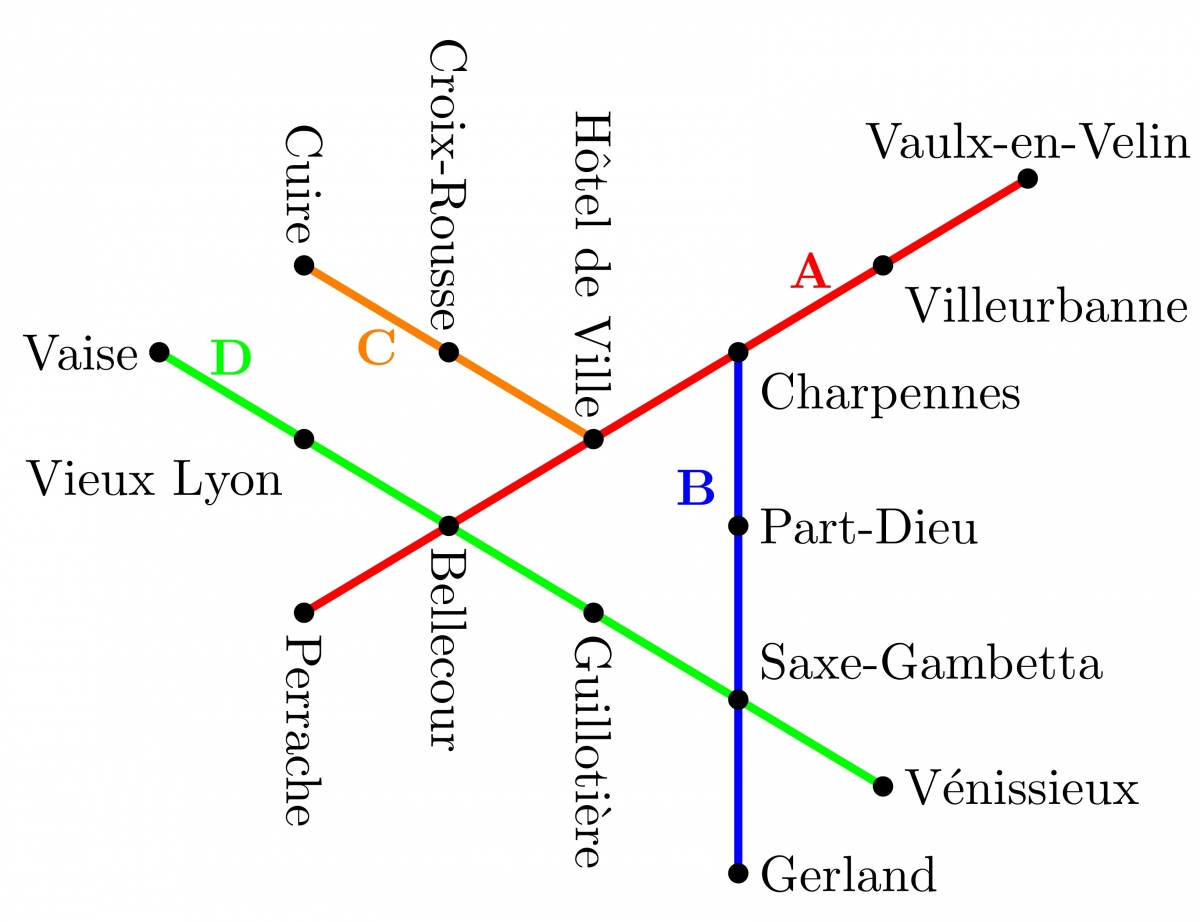
Exemple métropolitain : Considérez votre ville préférée équipée d'un réseau de métro. On note $\Omega$ l'ensemble des stations de ce réseau et $\Delta$ l'ensemble des lignes de métro (on identifie une ligne à l'ensemble des stations par lesquelles elle passe).
Dans notre exemple, on pourrait donc dire que les lignes $B$ et $C$ sont parallèles et qu'il n'y a pas à Lyon de point de concours entre trois lignes, mais on voit bien que le vocabulaire géométrique n'apporte ici pas grand chose.
Exemple graphé : Si $\Gamma$ est un graphe, on peut également le voir comme une structure d'incidence : il suffit de prendre les sommets comme points et les arêtes comme droites. Autrement dit, par définition, un graphe n'est rien d'autre qu'une structure d'incidence dont les droites sont des paires.
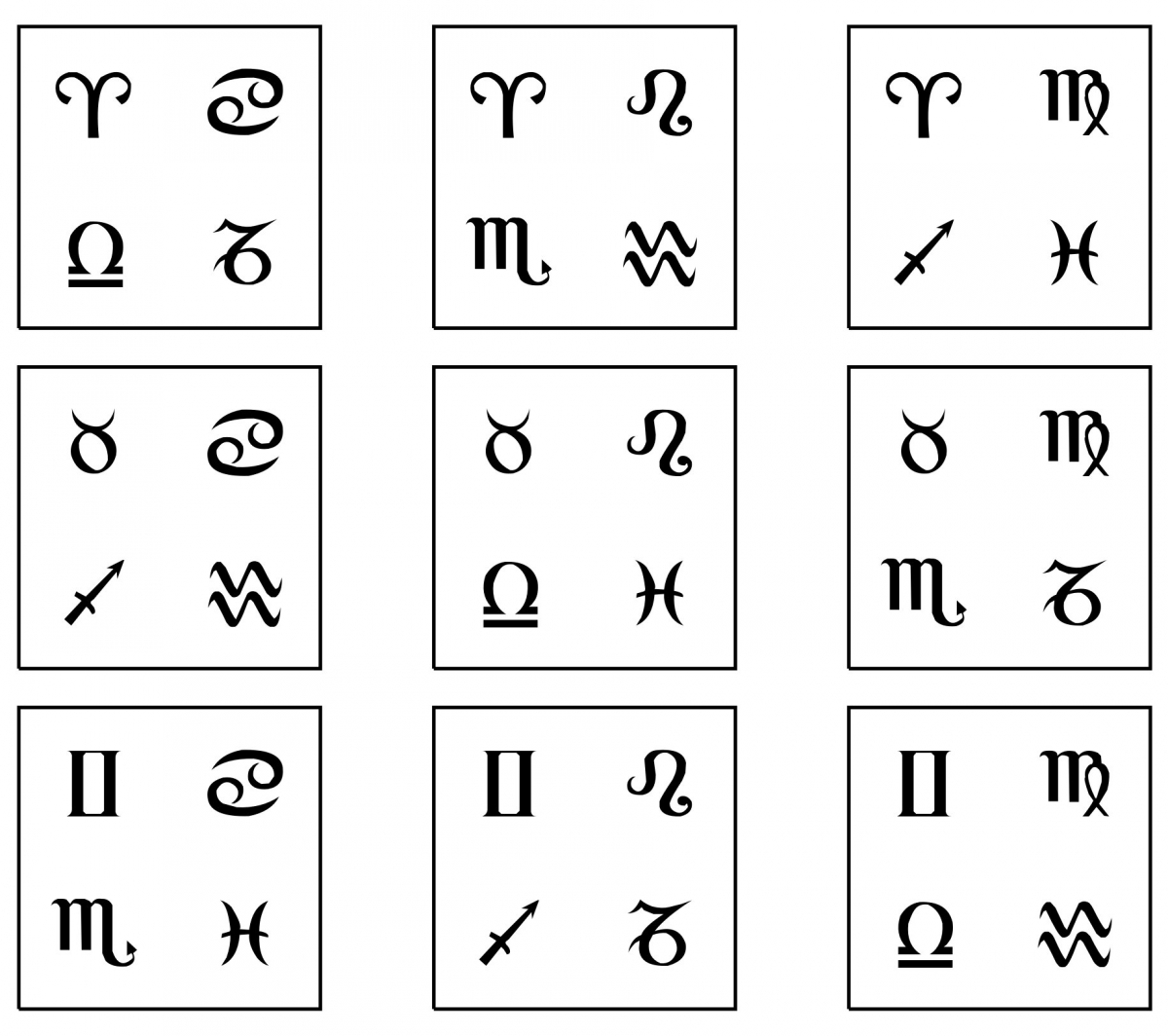
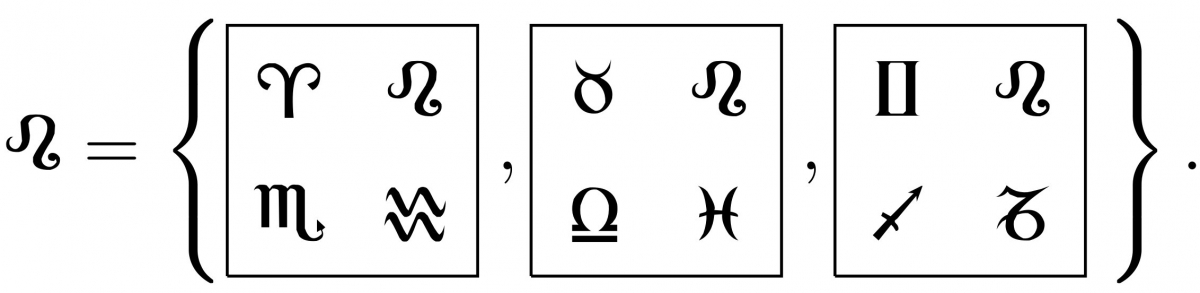
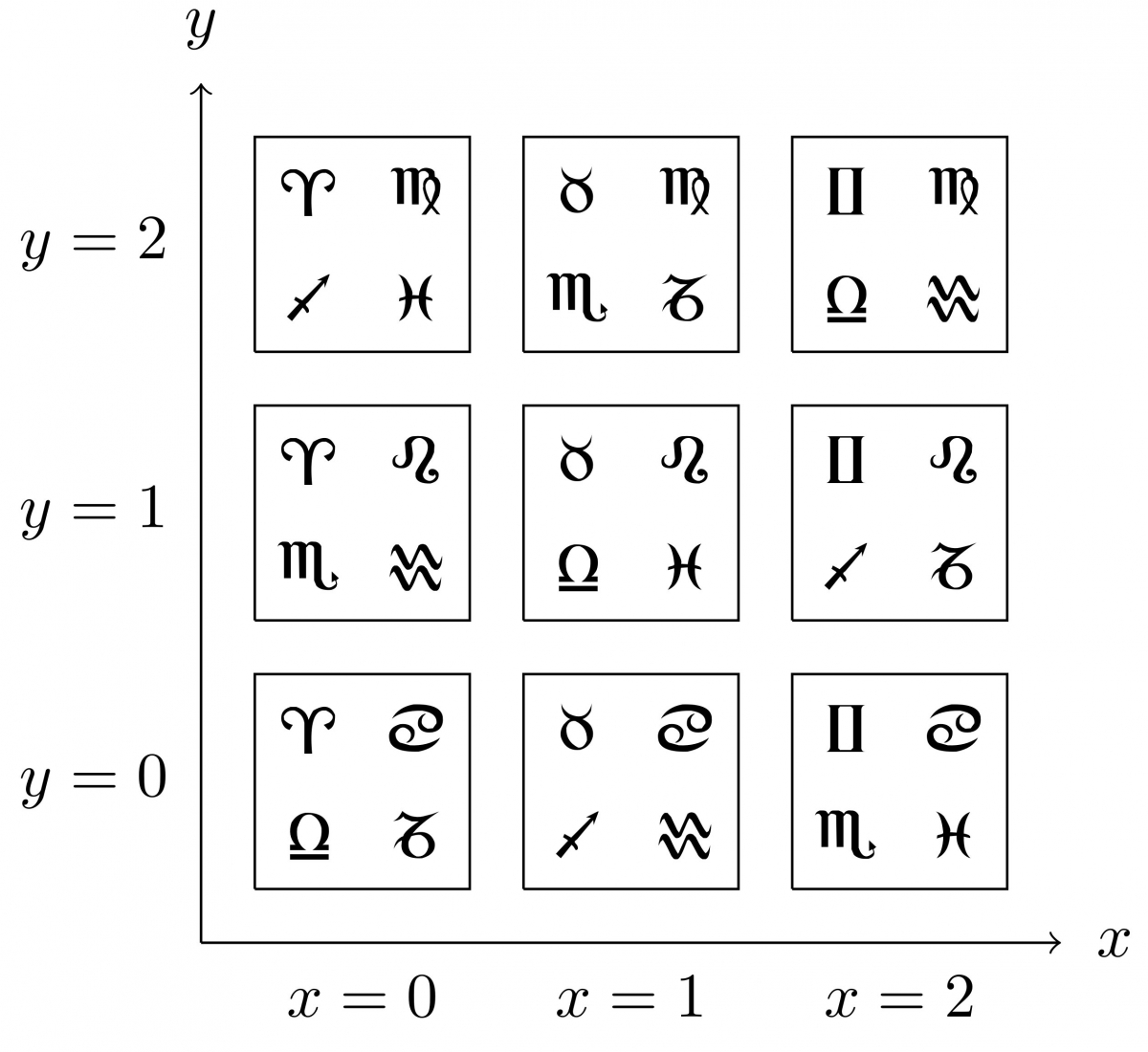
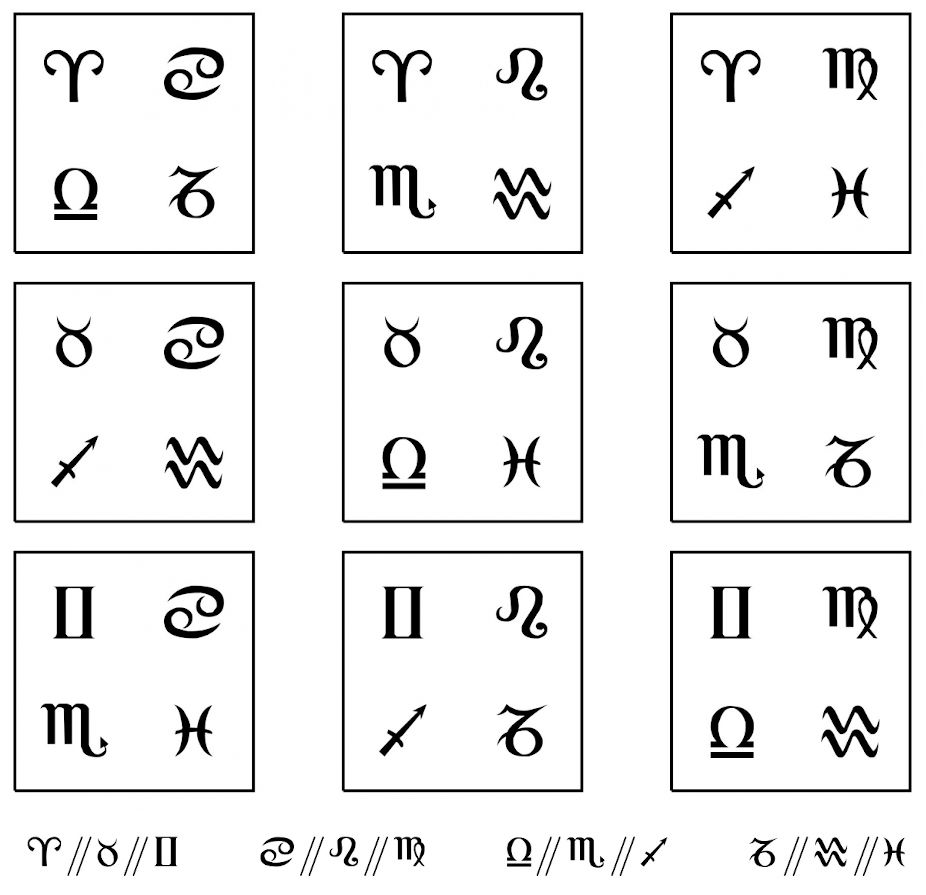
Exemple ludique : Dobble est un jeu de rapidité. Sur chacune des cartes sont imprimés 8 symboles et deux cartes quelconques ont toujours un unique symbole en commun. Pour simplifier, on va travailler avec une version simplifiée du jeu : notre jeu de miniDobble a 9 cartes, sur chacune desquelles sont imprimés 4 symboles.
L'interprétation de ce jeu comme structure d'incidence est un peu plus subtile : l'ensemble $\Omega$ des points est celui des cartes. Les symboles correspondent aux droites : chacun des symboles sera identifié avec l'ensemble des cartes qui le portent. Ainsi, dans notre jeu de miniDobble, on a par exemple la droite
Exemple ludique : Dobble est un jeu de rapidité. Sur chacune des cartes sont imprimés 8 symboles et deux cartes quelconques ont toujours un unique symbole en commun. Pour simplifier, on va travailler avec une version simplifiée du jeu : notre jeu de miniDobble a 9 cartes, sur chacune desquelles sont imprimés 4 symboles.
Notre miniDobble est donc une structure d'incidence à 9 points et 12 droites.
Qu'est-ce qu'un plan ?
Quelles sont les propriétés qui distinguent notre exemple usuel ? Pourquoi a-t-on envie de parler de droites dans le plan et pas forcément pour les lignes de métro ?
Une réponse possible est donnée par deux axiomes classiques de géométrie plane, qui ne parlent que de points et de droites et ont donc un sens dans notre contexte.
Axiome
Par deux points du plan passe une unique droite.
Axiome
(des parallèles) : Étant donné une droite δ et un point A, il existe une unique parallèle à δ passant par A.
Évidemment, notre exemple usuel vérifie ces deux axiomes. Qu'en est-il des autres ?
Sans trop de surprises, l'exemple métropolitain rate à peu près tout ce que l'on peut rater : deux stations peuvent ne pas être sur la même ligne et il peut y avoir à la fois « trop » et « pas assez » de parallèles (dans notre plan de Lyon simplifié, la ligne C a deux « parallèles » passant par Saxe-Gambetta et aucune passant par Vaulx-en-Velin).
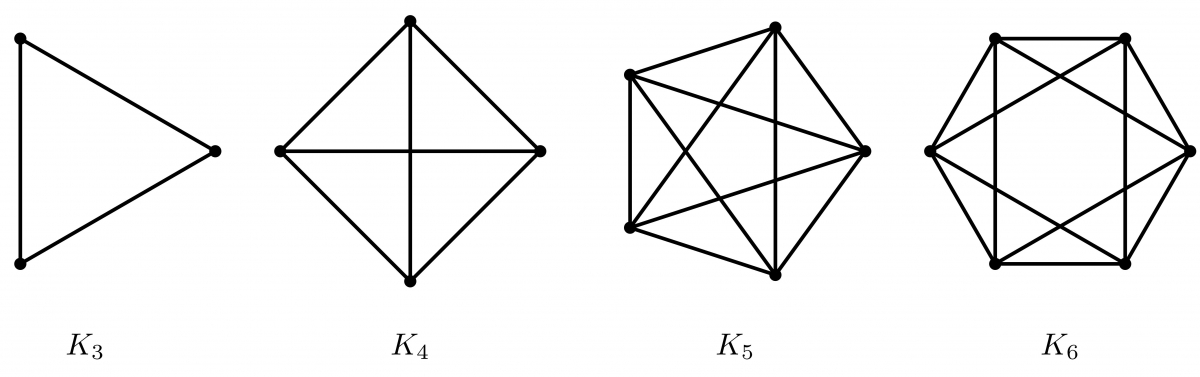
L'exemple graphé est un peu plus subtil. Dans ce contexte, l'axiome 1 est familier : il dit que deux sommets sont toujours adjacents, c'est-à-dire que le graphe est complet. Évidemment, la plupart des graphes ne sont pas complets, mais il reste toujours une infinité d'exemples satisfaisant l'axiome 1.
Que se passe-t-il pour l'axiome 2 ? Trois cas se présentent :
- Pour $K_3$, deux arêtes ont toujours un sommet en commun. Dans notre langage, il n'y a donc pas de droites parallèles et l'axiome 2 n'est pas vérifié.
- Pour $K_5$, étant donné trois sommets, par exemple $a$, $b$ et $c$, on voit que la droite-arête $\{a,b\}$ a plusieurs « parallèles » passant par $c$ : ici, $\{c,d \}$ et $\{c,e\}$. On vérifie facilement que ce phénomène continue (en fait, il s'empire) pour les graphes complets à plus de 5 sommets.
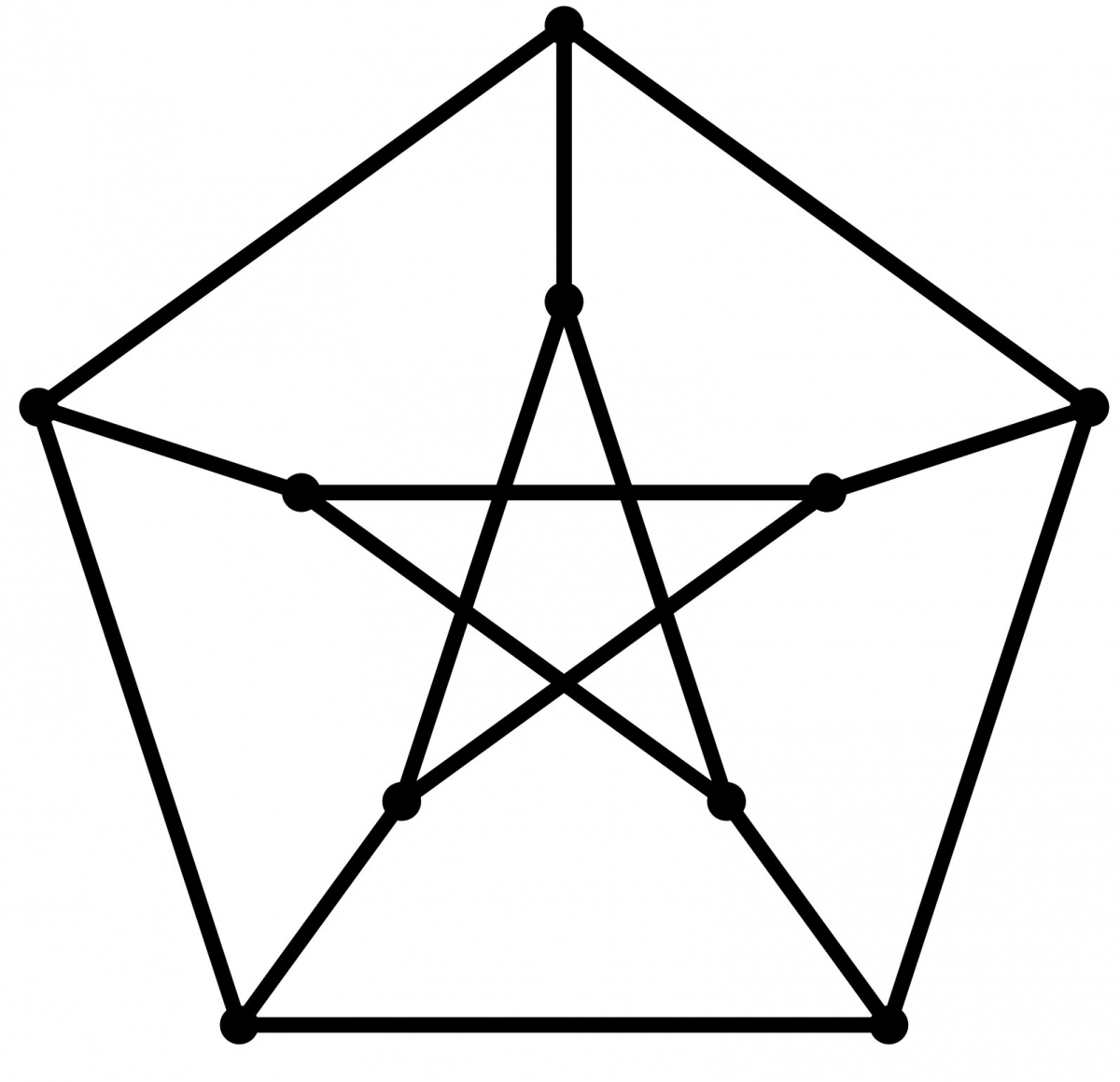
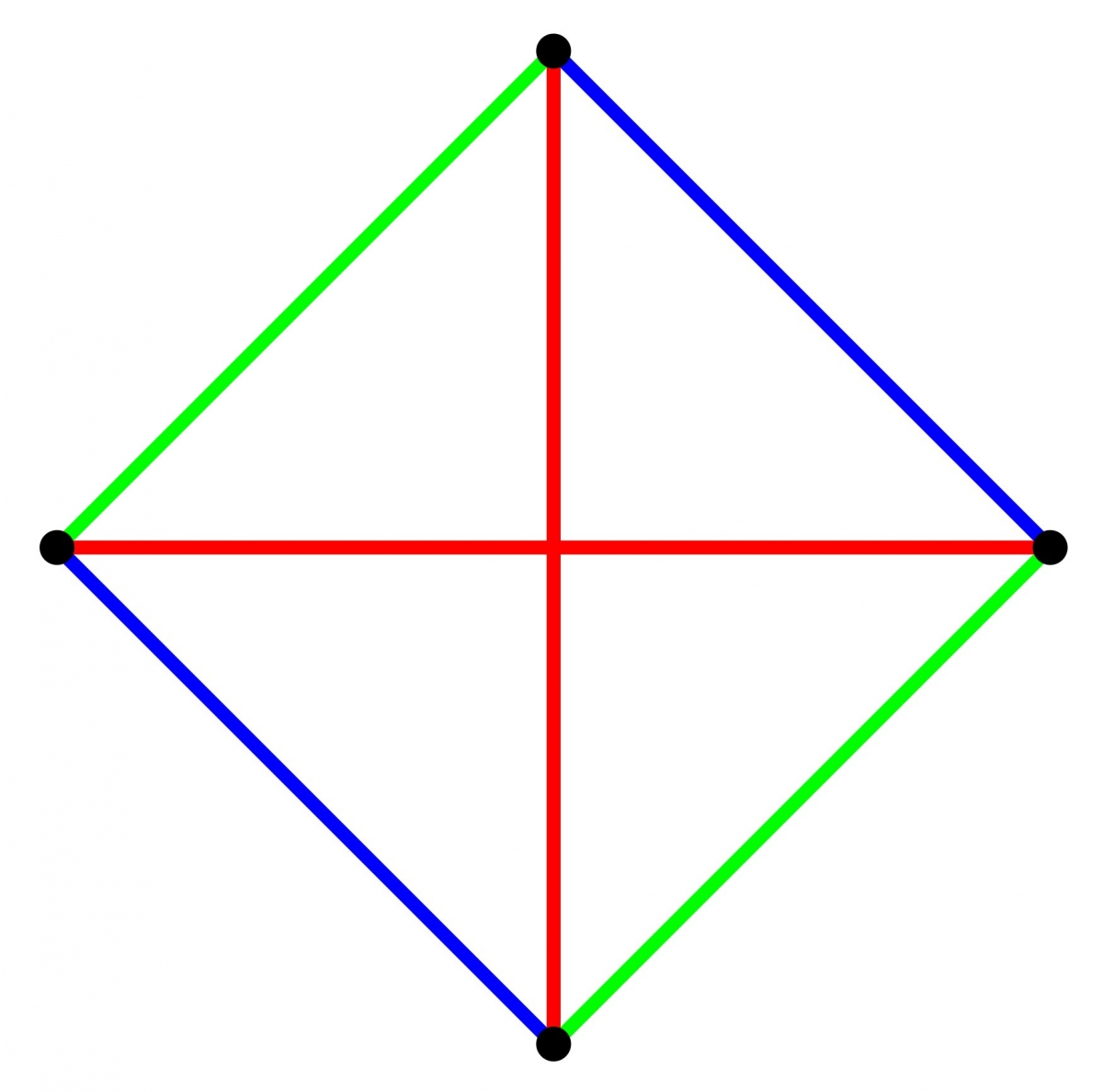
- Pour $K_4$, un miracle se produit : chaque droite a exactement une parallèle, et on vérifie facilement l'axiome 2. D'une certaine manière, $K_4$ est donc un « plan » à 4 points et à 6 droites. On reviendra sur cet exemple dans la section 4.
Pour notre exemple ludique, on a vu que les jeux de Dobble (le nôtre comme la version officielle) sont construits sur le principe que deux cartes ont toujours un unique symbole en commun. C'est tout bonnement l'axiome 1 dans ce contexte !
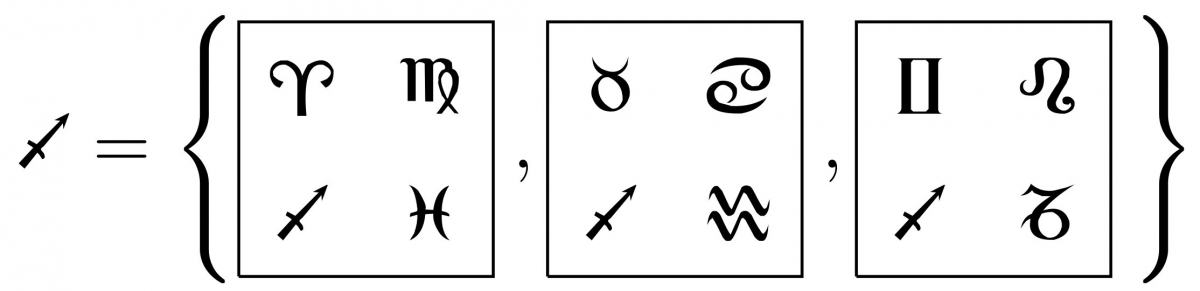
Pour l'axiome 2, la vérification est plus pénible, faute de comprendre encore comment les cartes ont été construites. On peut cependant le vérifier à la main laborieusement. Par exemple, l'unique « parallèle » à la droite
passant par
est la droite
Cette propriété sera plus claire quand on aura donné les secrets de fabrication de notre miniDobble.
Définition
Dans toute la suite, convenons d'appeler plan (affine) une structure d'incidence vérifiant les deux axiomes déjà énoncés ainsi que le suivant, qui n'est là que pour éviter des exemples sans intérêt (par exemple celui consistant à n'utiliser qu'une droite sur laquelle seraient tristement alignés tous les points).
Axiome
(de non-trivialité) : il existe quatre points trois à trois non alignés.
À ce stade, on a donc trois exemples de plans affines : l'exemple usuel, le graphe complet et le jeu de miniDobble. On peut se demander comment sont faits ces mystérieux exemples finis. On va pouvoir en dire plus, même si l'on verra que certaines questions d'apparence anodine ne sont toujours pas résolues. Mais auparavant, nous allons nous lancer dans une petite digression (si vous voulez éviter les chemins de traverse, la suite est à la section 4).
Aparté : le théorème de De Bruijn-Erdős ou Combien y a-t-il de droites ?
L'axiome 1 est sans doute la condition sine qua non pour parler de droites : après tout, lorsque l'on parle de la droite $(AB)$, c'est bel et bien qu'il existe une unique droite passant par les points $A$ et $B$.
On a vu que les structures d'incidence vérifiant l'axiome 1 ne manquaient pas : l'exemple usuel (qui a une infinité de points et de droites), les graphes complets $K_n$ (qui ont $n$ points et $\binom n 2$ droites), les jeux de Dobble (l'officiel, qui a 55 points et 57 droites et le nôtre, qui a 9 points et 12 droites). Il est également facile de construire des exemples géométriques à la pelle, en prenant un ensemble (fini ou infini) de points du plan ou de l'espace et en considérant l'ensemble de toutes les droites passant par ces points.
Il peut être étonnant de constater que l'on peut démontrer un théorème non trivial sur des objets aussi abondants.
Théorème
(De Bruijn et Erdős) : Soit $(\Omega, \Delta)$ une structure d'incidence possédant plus d'une droite et vérifiant l'axiome 1. Alors $|\Delta| \geq |\Omega|$.
En particulier, l'exemple géométrique que nous venons de présenter fournit un corollaire concret.
Corollaire géométrique
Soit $n$ points du plan ou de l'espace, pas tous alignés. Alors il passe par ces $n$ points au moins $n$ droites.
On constate d'ailleurs que cette borne est optimale.
Ce théorème est peut-être assez anecdotique, mais illustre bien le point de vue de la géométrie d'incidence : parfois, un résultat géométrique comme le corollaire que nous venons d'énoncer se déduit d'un résultat tout à fait combinatoire et ne fait pas du tout usage des purement géométriques comme ceux de distance, d'angle, etc.
La preuve du théorème repose sur le codage des structures d'incidence : comment peut-on représenter une structure d'incidence en termes d'objets mathématiques plus simples ? Une idée naturelle est celle de matrice d'incidence : on numérote les $p$ points $\Omega = \{ A_1, \ldots, A_p\}$ et les $q$ droites $\Delta = \{\delta_1, \ldots, \delta_q\}$ et l'on construit la matrice $I = I_{(\Omega, \Delta)} \in M_{p,q}(\mathbb R)$ dont le $(i,j)$-ième coefficient vaut $1$ si $A_i \in \delta_j$ et $0$ sinon. En formule, $$I_{(\Omega, \Delta)} = \left( [A_i \in \delta_j]\right)_{i,j} \in M_{p,q}(\mathbb R).$$
(On a utilisé une notation bien pratique : le crochet d'Iverson1$[P]$, qui vaut $1$ si la proposition $P$ est vraie et $0$ sinon). Un des intérêts de cette matrice (outre qu'elle permet de reconstruire complètement la structure d'incidence) est que le produit $I\cdot \vphantom{x}^t I$ a un sens : la matrice symétrique $S = I\cdot \vphantom{x}^t I \in M_p(\mathbb R)$ est une matrice carrée telle que $$\begin{array}{r@{}l} S_{i,j} = \sum_{k=1}^q I_{i,k} \cdot \vphantom{x}^tI_{k,j} &= \sum_{k=1}^q I_{i,k} I_{j,k} \\ &= \sum_{k=1}^q [A_i \in \delta_k] \cdot [A_j \in \delta_k] \\ &= \sum_{k=1}^q [\{ A_i, A_j \} \subset \delta_k]. \end{array}$$
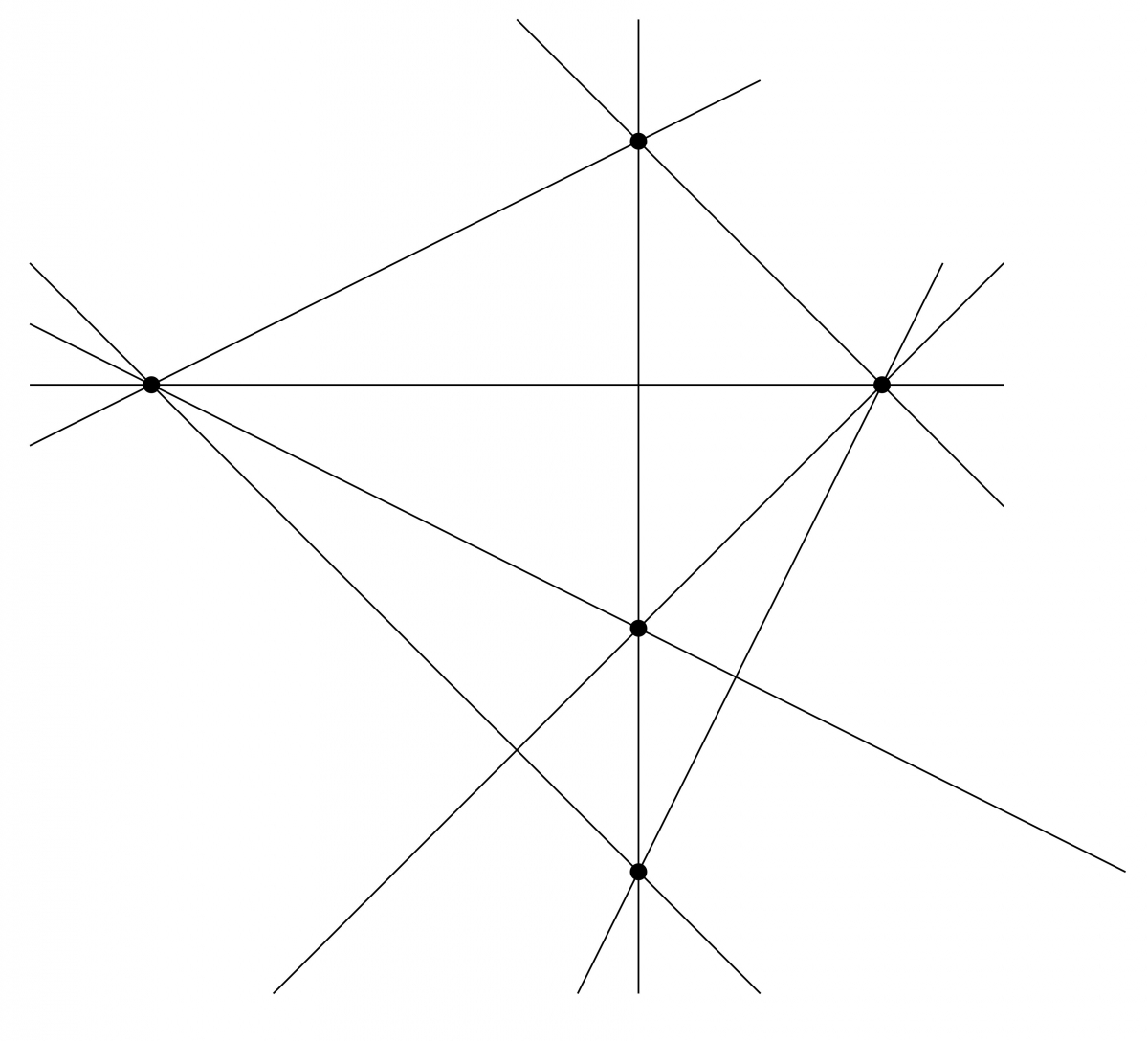
Autrement dit $S_{i,j}$ est le nombre de droites passant à la fois par $A_i$ et par $A_j$. Si $i \neq j$, ce nombre est $1$ d'après l'axiome 1 : il n'y a qu'une seule telle droite, et c'est précisément la droite $(A_i A_j)$. En revanche, si $i=j$, c'est le nombre $r_i = S_{i,i}$ de droites passant par $A_i$ peut varier (dans la figure précédente, par exemple, il vaut $n-1$ ou $2$ suivant le point considéré). On peut tout de même dire que $r_i \geq 2$. Si ce n'était pas le cas, tous les points seraient sur l'unique droite passant par $A_i$, ce qui entraînerait que les points sont alignés, situation que l'on a exclue.
On va alors conclure à l'aide du lemme suivant d'algèbre linéaire.
Lemme
Soit $r_1, \ldots, r_p > 1$ (dans notre situation, ce sont des entiers, mais cela ne joue ici aucun rôle). Alors la matrice $$S = \begin{pmatrix} r_1 & 1 & \ldots & 1\\ 1 & r_2 & \ldots & 1 \\ \vdots & \vdots & \ddots & \vdots \\ 1 & 1 & \ldots & r_p \end{pmatrix} \in M_p(\mathbb R)$$ est inversible.
Ce lemme permet de conclure : puisque $S = I \cdot \vphantom x^t I$ est inversible, cette matrice est de rang $p$. Puisque $I$ en est un facteur, elle est elle-même de rang au moins $p$. Mais c'est une matrice de taille $p \times q$, et donc de rang $\leq \min(p,q)$. Cela entraîne bien $p\leq q$.
Le lemme peut se démontrer par un calcul un peu laborieux de déterminant. Une solution plus élégante (mais demandant plus de résultats et pas très naturelle) consiste à écrire la matrice $S$ sous la forme $S = J + \mathrm{diag}(r_1 - 1, \ldots, r_p - 1)$, où $J$ est la matrice dont tous les coefficients valent 1. Il n'est pas très difficile de voir que la matrice $J$ a un noyau de dimension $p-1$. Puisqu'elle est de trace $p$, elle a donc pour valeurs propres $p$ (valeur propre simple) et $0$ (valeur propre $(p-1)$-uple). Cela entraîne que la matrice $J$ est symétrique positive. Comme $\mathrm{diag}(r_1 - 1, \ldots, r_p - 1)$ est symétrique définie positive (car $r_i - 1 > 0$), leur somme $S$ est aussi symétrique définie positive et donc inversible.
Une famille de plans
Les coordonnées cartésiennes permettent de donner une définition algébrique du plan usuel : ses points sont les couples $(x, y)$ de réels et les droites sont données par les équations $ax + b y + c = 0$ (où $a$, $b$ et $c$ sont des réels tels que $(a,b)\neq(0,0)$).
Le point-clef de cette section est que cette construction ne dépend pas du fait que nos nombres sont réels : on peut mener cette construction sur n'importe quel corps $K$ !
Proposition et définition
Soit $K$ un corps. On pose $\Omega = K^2$ et $\Delta = \left\{ \delta_{a,b,c} \, \middle | \, (a,b,c) \in K^3 \, \mathrm{tq}\, (a,b) \neq (0,0) \right\}$ où l'on a noté $\delta_{a,b,c} = \left\{ (x,y) \in K^2 \, \middle | \, ax+by+c = 0 \right\}$. Alors $(\Omega, \Delta)$ est un plan affine, que l'on notera $\mathbb A^2(K)$ et que l'on appellera plan (affine) sur le corps $K$.
Remarque : Si $(a',b',c') = \lambda (a,b,c)$, on a $\delta_{a,b,c} = \delta_{a',b',c'}$.
Preuve : On vérifie facilement que les formules usuelles conviennent :
- il y a une unique droite passant par $(x_1, y_1)$ et $(x_2, y_2)$, celle d'équation $ax+by+c=0$ avec $a = y_1 - y_2$, $b = x_2 - x_1$ et $c = x_1 y_2 - x_2 y_1$.
- l'unique droite parallèle à $\delta_{a,b,c}$ passant par $(x,y)$ est $\delta_{a',b',c'}$, où $c' = -(ax+by)$.
Rétrospectivement, notre exemple usuel n'était donc que $\mathbb A^2(\mathbb R)$. Mais cela permet également de définir des exemples finis. Si $p$ est un nombre premier, l'ensemble $\mathbb Z / p \mathbb Z = \left \{ \bar 0, \bar 1, \ldots, \overline{p-1} \right\}$ des entiers modulo $p$ est un corps, que l'on note en général $\mathbb F_p$ et l'on a un plan $\mathbb A^2(\mathbb F_p)$. $\square$
Proposition
Si $K$ a $q$ éléments, $\mathbb A^2(K)$ a $q^2$ points et $q^2 + q$ droites.
Preuve : $\Omega = K^2$ est simplement constitué des paires d'éléments de $K$ et a donc $q^2$ éléments.
Pour les droites, remarquons qu'au lieu de travailler avec les équations de la forme $ax+by+c = 0$, toute droite, comme sur le corps des réels, se met uniquement sous la forme $y = m x + h$ si $b \neq 0$ (avec $m = - a / b$ et $h = -c/b$) et que, dans le cas contraire, on a $a \neq 0$ et la droite se met uniquement sous la forme $x = x_0$ (avec $x_0 = -c/a$). On a donc $q^2$ droites de la forme $y = mx + h$ (il y a $q$ choix pour $m$ et autant pour $h$) et $q$ droites de la forme $x = x_0$. On retrouve donc le total de $q^2 + q$ droites annoncé. $\square$
On vient donc de construire un plan pour chaque corps $K$. Regardons le cas deux corps les plus petits, $\mathbb F_2$ et $\mathbb F_3$.
Les tables d'addition et de multiplication de $\mathbb F_2 = \{ 0, 1 \}$ sont $$\begin{array}{c|cc} + & 0 & 1 \\ \hline 0 & 0 & 1 \\ 1 & 1 & 0 \end{array} \qquad \begin{array}{c|cc} \times & 0 & 1 \\ \hline 0 & 0 & 0 \\ 1 & 0 & 1 \end{array}$$
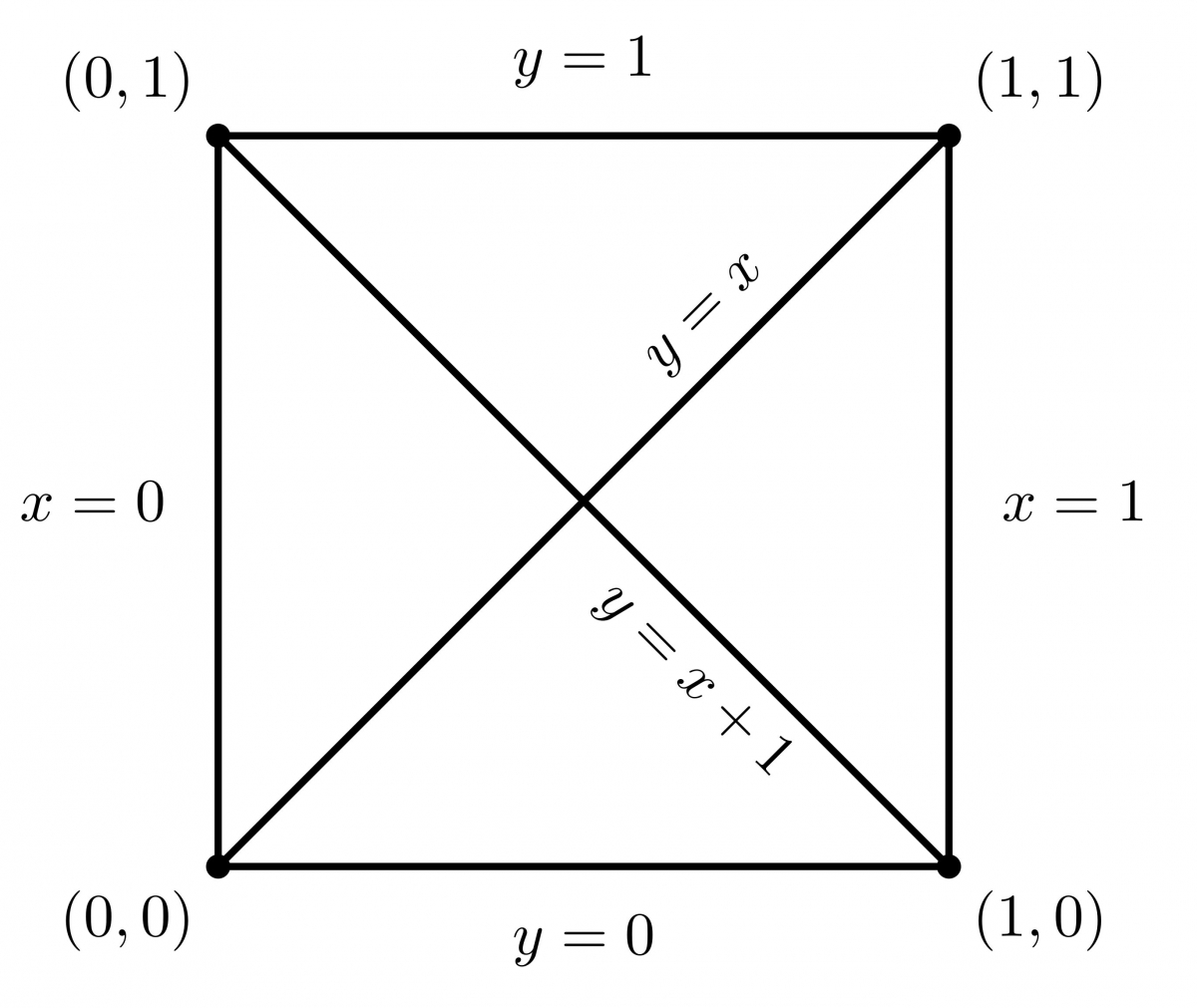
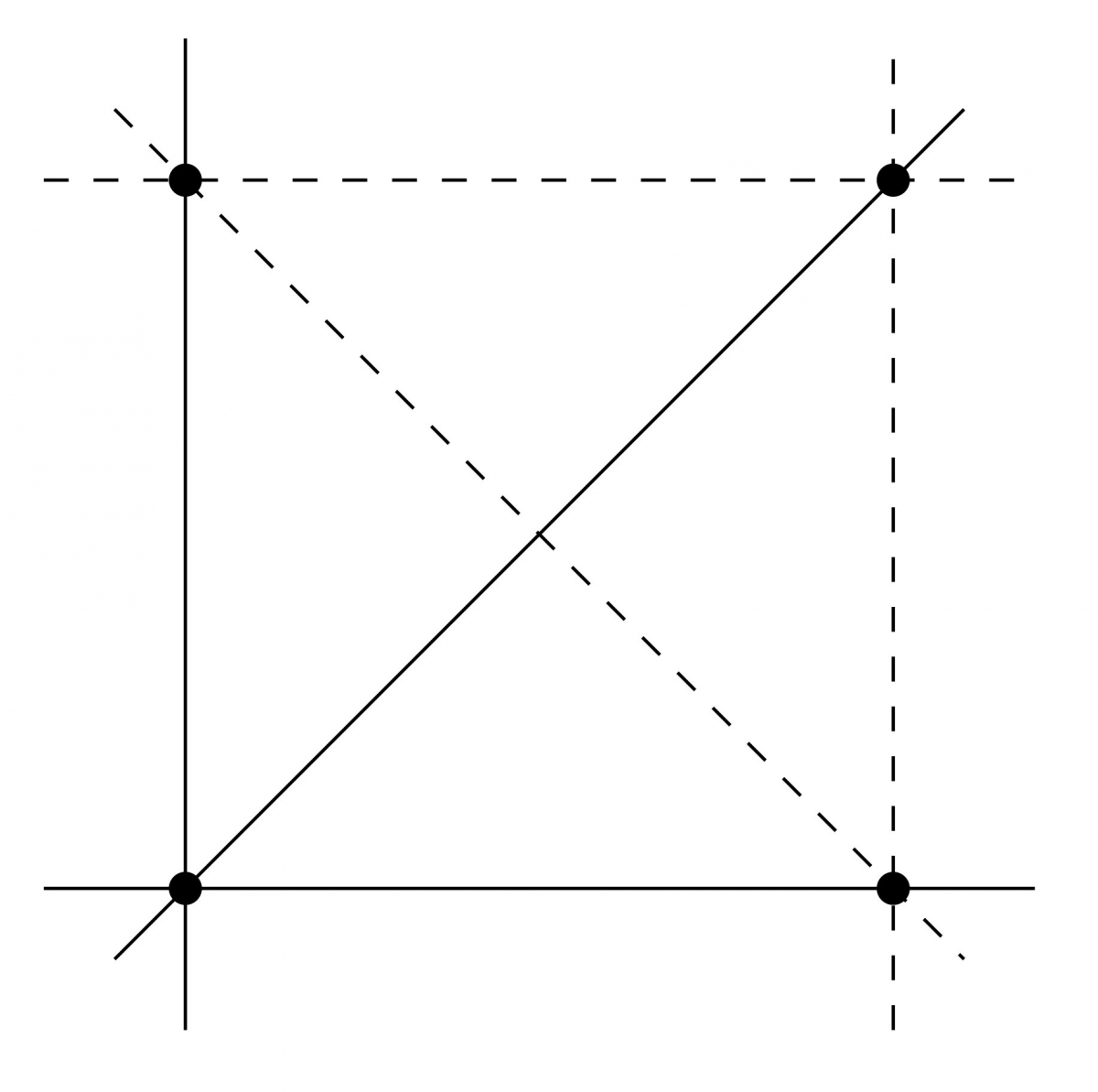
$\mathbb A^2(\mathbb F_2)$ a alors $4=2^2$ points : $(0,0)$, $(0,1)$, $(1,0)$, $(1,1)$ et $6 = 2^2 + 2$ droites (remarquez qu'ici $-x = x$) : $$\begin{array}{cc} \delta_{0,1,0} = \{ y = 0 \} = \{(0,0), (1,0)\} & \delta_{0,1,1} = \{ y = 1 \} = \{(0,1), (1,1)\}\\ \delta_{1,0,0} = \{ x = 0 \} = \{ (0,0), (0,1) \} & \delta_{1,0,1} = \{ x = 1 \} = \{ (1,0), (1,1) \}\\ \delta_{1,1,0} = \{y=x\} = \{(0,0), (1,1)\} & \delta_{1,1,1} = \{ y = x+1 \} = \{ (0,1), (1,0) \}\end{array}$$
Autrement dit, il y a $4$ points et les droites sont simplement toutes les paires de points. Bref, $\mathbb A^2(\mathbb F_2)$ n'est rien d'autre que $K_4$.
Si l'on passe maintenant à $\mathbb F_3 = \{0, 1, 2\}$, on a les tables d'opération $$\begin{array}{c|ccc} + & 0 & 1 & 2 \\ \hline 0 & 0 & 1 & 2 \\ 1 & 1 & 2&0 \\ 2 & 2 & 0 & 1 \end{array} \qquad \begin{array}{c|ccc} \times & 0 & 1 & 2\\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 2 \\ 2 & 0 & 2 &1 \end{array}$$
Il y a alors $3^2 = 9$ points et $3^2 + 3 = 12$ droites. On peut vérifier que ce n'est rien d'autre que notre jeu de miniDobble.
À quelle point notre recette est-elle flexible pour fabriquer des plans finis ?
Un résultat classique mais non trivial affirme qu'il existe un corps à $q$ éléments si et seulement si $q = p^e$ est la puissance d'un nombre premier. Dans ce cas, en outre, le corps est unique et on le note $\mathbb F_q$. Dans le cas où $q = p$ est un nombre premier, on a vu que $\mathbb F_p = \mathbb Z/p\mathbb Z$ est simplement l'ensemble des entiers modulo $p$. (Attention ! $\mathbb Z/n\mathbb Z$ n'est un corps que si $n$ est premier. En particulier, $\mathbb F_4$, par exemple, n'est pas $\mathbb Z/4\mathbb Z$ !)
On a donc obtenu des plans finis $\mathbb A^2(\mathbb F_q)$ pour $q=p^e$ (qui ont $q^2$ points et $q^2 + q$ droites) mais aussi le plan $\mathbb A^2(\mathbb Q)$ (qui est simplement composé des points du plan usuel à coordonnées rationnelles et des droites dont l'équation est à coefficients rationnels), un plan \mathbb A^2(\mathbb C)$ assez difficile à se représenter, etc.
La section suivante a pour but de déterminer dans quelle mesure un plan affine fini ressemble aux exemples « standard » que nous venons de présenter.
Structures des plans finis
Dans cette section, nous allons voir à quel point les axiomes 1, 2 et 3 énoncés plus haut forcent les plans finis à ressembler à $\mathbb A^2(\mathbb F_q)$.
Théorème
Soit $(\Omega, \Delta)$ un plan. La relation de parallélisme est alors une relation d'équivalence sur $\Delta$. En outre, deux droites non parallèles s'intersectent en un point unique.
Preuve :
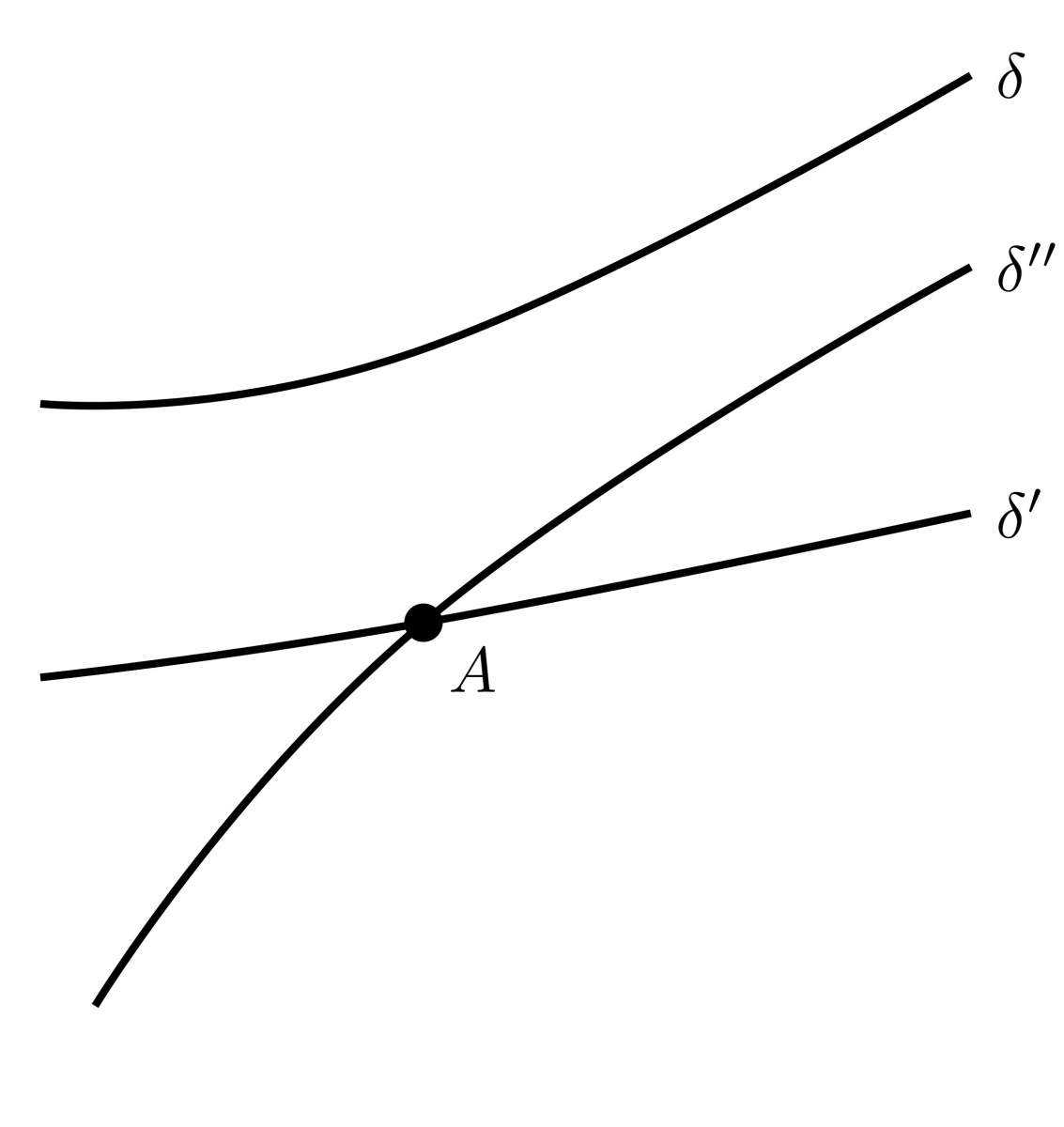
- La relation de parallélisme est clairement réflexive et symétrique. Soit $\delta$, $\delta'$ et $\delta''$ trois droites telles que $\delta \mathbin{\!/\mkern-5mu/\!} \delta'$ et $\delta \mathbin{\!/\mkern-5mu/\!} \delta''$. Supposons par l'absurde que $\delta'$ et $\delta''$ ne soient pas parallèles et prenons un point $A$ appartenant à la fois à $\delta$ et à $\delta'$. On voit alors que $\delta$ a (au moins) deux parallèles passant par $A$, au mépris de l'axiome 2.
- On peut reformuler le deuxième énoncé en disant que deux droites différentes ne s'intersectent jamais en plus d'un point. Supposons donc, par l'absurde, qu'il existe $\delta'$ et $\delta''$ ayant au moins deux points d'intersection $A$ et $B$. Il y a alors deux droites passant par $A$ et $B$, au mépris de l'axiome 1.
Remarque : L'ensemble des droites parallèles a une droite donnée sera appelé, comme dans le cas classique, la direction de la droite.
Théorème
Soit $(\Omega, \Delta)$ un plan fini. Alors toutes les droites ont le même nombre d'éléments $n$, tout point appartient est sur exactement $n+1$ droites, et $\Omega$ a $n^2$ points.
Preuve : Regardons (pour changer) l'axiome 3. Puisqu'il existe $4$ points sans aucun triplet de points alignés (on parle de quadrangle), il existe $3$ droites concourantes.
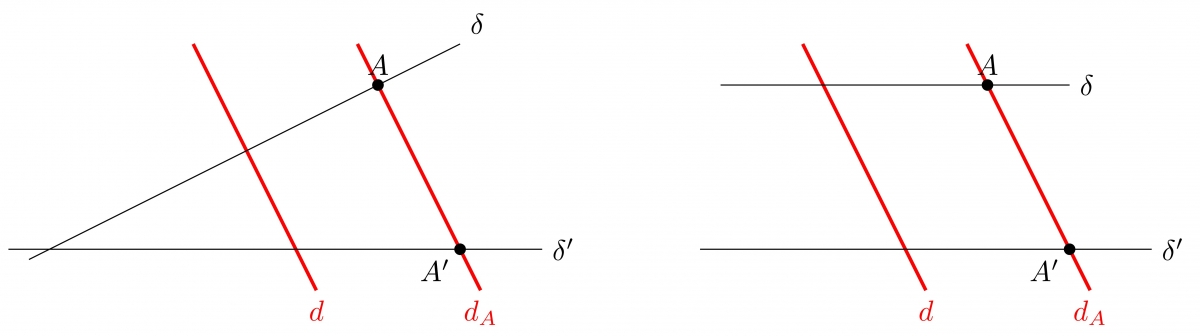
En particulier, il existe au moins trois directions. Cela implique qu'étant donné deux droites $\delta$ et $\delta'$, on pourra toujours trouver une droite $d$ qui ne soit parallèle ni à $\delta$ ni à $\delta'$. Fixons-en une. On a alors une transforamtion qui envoie les points de $\delta$ sur ceux de $\delta'$ : si $A \in \delta$, il existe une unique droite $d_A$ passant par $A$ et parallèle à $d$. Cette droite intersecte $\delta'$ en unique point $A' = \phi(A)$. En résumé, on peut dire que $\phi$ est la projection sur $\delta'$ parallèlement à $d$.
On vérifie alors que la projection sur $\delta$ parallèlement à $d$ est la réciproque de $\phi$ ce qui entraîne que $\phi$ est bijective et donc que $\delta$ et $\delta'$ ont le même nombre d'éléments $n$.
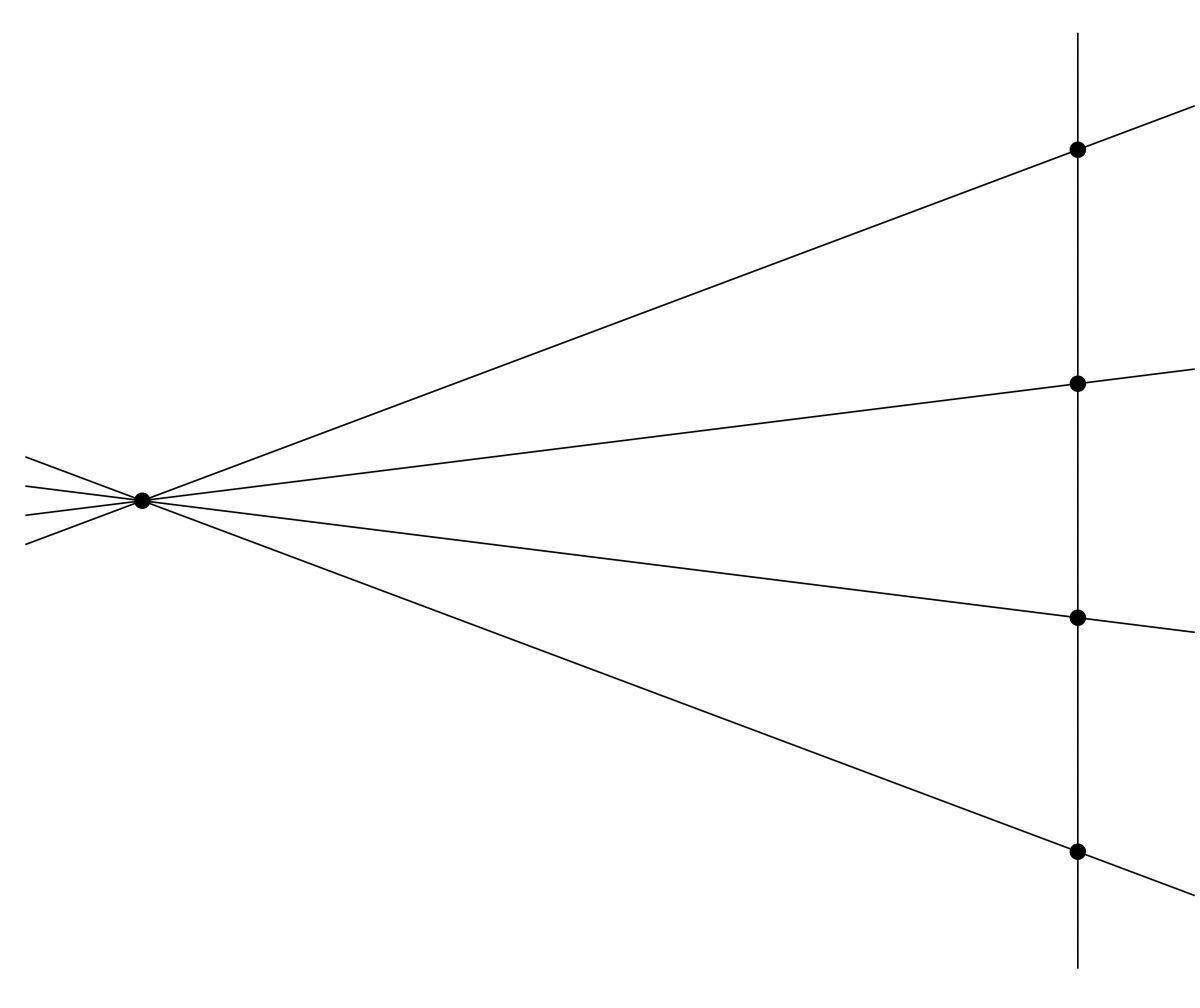
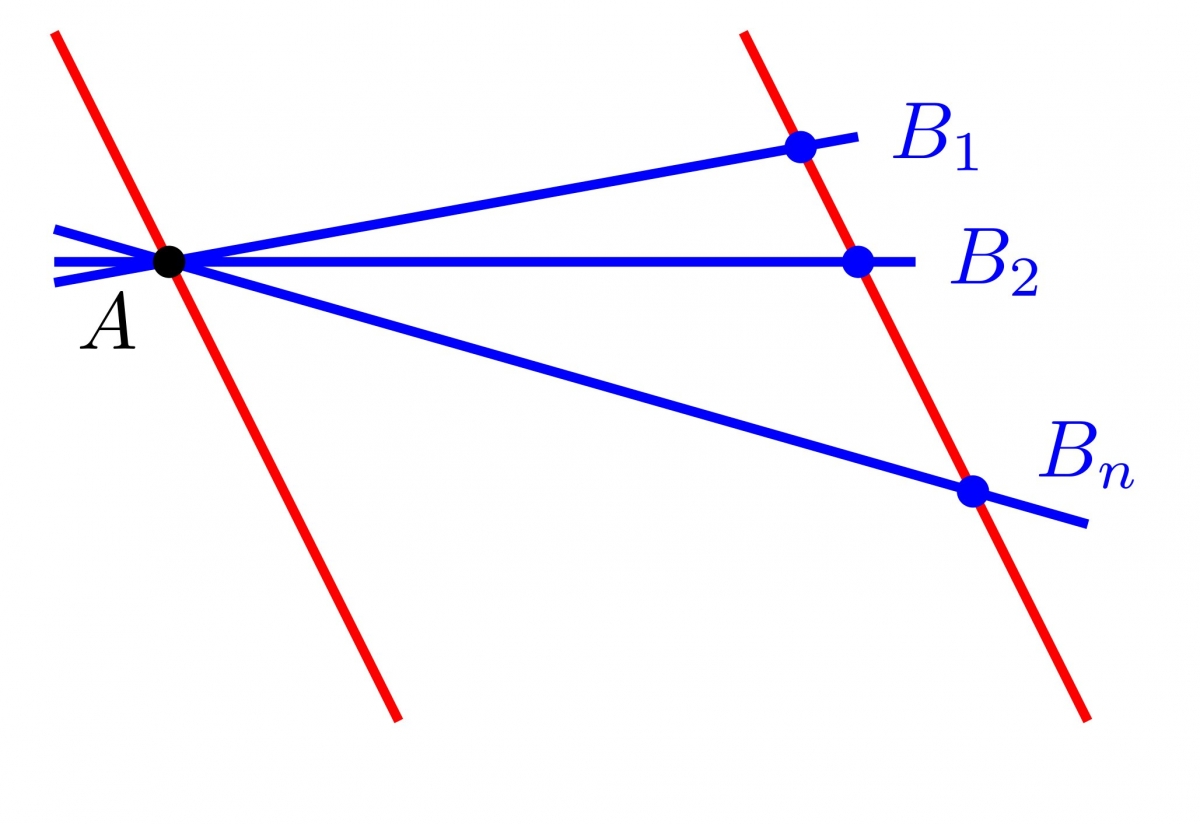
On peut en déduire que par un point donné passent toujours $n+1$ droites : si $A \in \Omega$ et $\delta \in \Delta$ sont fixés, les droites passant par $A$ sont de deux types :
- l'unique droite parallèle à $\delta$.
- les droites intersectant $\delta$, c'est-à-dire les droites $(AB)$, pour $B$ parcourant $\delta$. Il y a $n$ telles droites, une par point de $\delta$.
Comme toute droite est parallèle à une unique droite passant par $A$, on en déduit qu'il y a en tout $n+1$ directions.
cela permet enfin de compter les points de $\Omega$. Chaque point $B$ de $\Omega \setminus \{A\}$ définit une unique droite $(AB)$ passant par $A$. Toute droite passant par $A$ peut être obtenue ainsi, donc l'application $$\begin{array}{ccc} \Omega \setminus \{A\} & \to & \{\text{droites passant par }A\} \\ B & \mapsto & (AB) \end{array}$$ est surjective. Or, si $B \neq A$, tous les points $B'$ de $(AB) \setminus \{A\}$ (il y en a $n-1$) définissent la même droite $(AB') = (AB)$. D'après le lemme des bergers, on a donc $$\frac{|\Omega \setminus \{A\}|}{n-1} = |\{\text{droites passant par }A\}| = n+1.$$ Autrement dit $|\Omega| = 1 + (n-1)(n+1) = n^2$.
On a vu que si $\mathbb F_q$ est le corps à $q$ éléments, le plan $\mathbb A^2(\mathbb F_q)$ a $q^2$ éléments. Il est donc d'ordre $n$. Comme un tel corps n'existe que quand $q$ est une puissance d'un nombre premier, cette construction ne permet pas de construire de plans pour un ordre différent. À vrai dire, à l'heure actuelle, personne ne sait construire un tel plan.
Question ouverte : Y a-t-il des plans affines d'ordre $n$, pour un entier $n$ qui ne soit pas la puissance d'un nombre premier ?
Par ordre chronologique, voilà les résultats (partiels) connus sur cette question :
- En 1938, le combinatoricien Indien Raj Chandra Bose démontre qu'il n'y a pas de plan d'ordre 6. On reviendra sur cette preuve lors de la prochaine (et dernière !) section.
- En 1949, Bruck et Ryser démontrent le seul résultat connu aujourd'hui de non-existence qui s'applique à un infinité d'entiers n :
Théorème : S'il existe un plan d'ordre $n$ avec $n$ congru à 1 ou à 2 modulo 4, alors $n$ est la somme de deux carrés.
Notons que comme 6 est congru à 2 modulo 6 sans être la somme de deux carrés, ce résultat enraîne celui de Bose. - En 1988, à la suite de presque dix ans de travaux de plusieurs chercheurs et grâce à l'utilisation d'un ordinateur, Lam, Thiel et Swiercz ont pu conclure qu'il n'y avait pas de plan d'ordre 10.
La résolution ne serait-ce que d'un cas supplémentaire serait une avancée significative dans ce domaine.
Le problème des 36 officiers
En 1782, au début d'un mémoire intitulé Recherches sur une nouvelle espèce de quarrés magiques, Leonhard Euler écrit :
Une question fort curieuse, qui a exercé pendant quelque temps la sagacité de bien du monde, m'a engagé à faire les recherches suivantes, qui semblent ouvrir une nouvelle carrière dans l'Analyse, et en particulier dans la doctrine des combinaisons. Cette question rouloit sur une assemblée de 36 Officiers de six différens grades et tirés de six Régimens différens, qu'il s'agissoit de ranger dans un quarré, de manière que sur chaque ligne tant horizontale que verticale il se trouva six Officiers tant de différens caractères que de Régimens différens. Or, après toutes les peines qu'on s'est donné pour resoudre ce Probléme, on a été obligé de reconnoître, qu'un tel arrangement est absolument impossible, quoiqu'on ne puisse pas en donner de démonstration rigoureuse.
Pour mieux expliquer l'étât de la question mentionnée, je marquerai les six Régimens différens par les lettres latines a, b, c, d, e, f, et les six différens grades par les grecques $\alpha$, $\beta$, $\gamma$, $\delta$, $\epsilon$, $\zeta$, et il est clair que le Caractère de chaque Officier est déterminé par deux lettres, l'une latine, et l'autre grecque, dont la première marque son Régiment, et l'autre son grade et qu'il y aura en effet trente six combinaisons de ces lettres, que voicié :$$\begin{array}{cccccc} \textrm{a} \alpha & \textrm{a} \beta & \textrm{a} \gamma & \textrm{a} \delta & \textrm{a} \epsilon & \textrm{a} \zeta\\ \textrm{b} \alpha & \textrm{b} \beta & \textrm{b} \gamma & \textrm{b} \delta & \textrm{b} \epsilon & \textrm{b} \zeta\\ \textrm{c} \alpha & \textrm{c} \beta & \textrm{c} \gamma & \textrm{c} \delta & \textrm{c} \epsilon & \textrm{c} \zeta\\ \textrm{d} \alpha & \textrm{d} \beta & \textrm{d} \gamma & \textrm{d} \delta & \textrm{d} \epsilon & \textrm{d} \zeta\\ \textrm{e} \alpha & \textrm{e} \beta & \textrm{e} \gamma & \textrm{e} \delta & \textrm{e} \epsilon & \textrm{e} \zeta\\ \textrm{f} \alpha & \textrm{f} \beta & \textrm{f} \gamma & \textrm{f} \delta & \textrm{f} \epsilon & \textrm{f} \zeta \end{array}$$ dont chacune exprime le caractère d'un Officier. Il s'agit donc d'inscrire ces 36 termes dans les 36 cases d'un quarré, en sorte que sur chaque bande tant horizontale que verticale on rencontre tant les six lettres latines que les grecques.
Donnons deux définitions utiles pour discuter ce problème des 36 officiers.
Définitions
- Un carré latin d'ordre $n$ est la donnée d'un tableau $(A_{i,j})_{i,j}$ de taille $n \times n$ rempli par $n$ symboles $a_1, \ldots, a_n$ de telle sorte qu'un symbole ne se répète jamais sur la même ligne ou la même colonne.
- Deux carrés latins $A$ et $B$ d'ordre $n$ (et de symboles $a_1, \ldots, a_n$ et $b_1, \ldots, b_n$, respectivement) sont dits orthogonaux si pour chaque couple $(a_r, b_s)$ de symboles, il existe des indices $1 \leq i, j \leq n$ tels que $A_{i,j}=a_r$ et $B_{i,j} = s$.
Dans ce langage, la question d'Euler est donc de déterminer s'il est possible de construire deux carrés latins d'ordre 6 orthogonaux. (Suite à la notation utilisée par Euler, un tel couple de carrés latins orthogonaux est souvent appelé carré gréco-latin).
Euler a en fait construit des carrés gréco-latins d'ordre $n$ pour tout $n$ impair ou multiple de $4$. Il est très facile de voir qu'il n'en existe pas d'ordre 2. Euler a même conjecturé qu'il n'existait aucun carré gréco latin d'ordre congru à 2 modulo 4.
La première résolution du problème des 36 officiers est due à Gaston Tarry, par une disjonction soigneuse de cas. Il existe aujourd'hui d'autres preuvex, mais aucune n'est complètement simple ou éclairante. En revanche, une vérification exhaustive est aujoud'hui relativement aisée pour un ordinateur.
Cependant, le reste de la conjecture d'Euler est complètement faux : en 1960, Bose, Shrikhande et Parker ont définitivement réglé le problème en construisant des carrés gréco-latins d'ordre $n$, pour tout $n \neq 2, 6$.
Quelle est le rapport entre cette histoire et nos plans d'ordre $n$ ? Le lien vient d'un théorème du même Bose :
Théorème
(Bose, 1938) : Il existe un plan d'ordre $n$ si et seulement si l'on peut trouver $(n-1)$ carrés latins d'ordre $n$ qui soient mutuellement orthogonaux.
Nous allons simplement démontrer le sens direct (la réciproque n'est pas difficile à reconstruire à partir de la construction, due à Bose, que l'on va donner). En particulier, cela démontrera l'absence de plan d'ordre 6 (un tel plan donnerait d'après le théorème de Bose l'existence de cinq carrés latins mutuellement orthogonaux alors que le problème des 36 officiers dit déjà qu'il est impossible d'en trouver deux).
Soit donc $(\Omega, \Delta)$ un plan d'ordre $n$. Comme on l'a vu, il y a $n^2$ points dans $\Omega$ et $n^2 + n$ droites dans $\Delta$, regroupées en $n+1$ directions, c'est-à-dire en $n+1$ paquets de $n$ droites parallèles.
Choisissons deux directions et numérotons $(d_1, \ldots, d_n)$ et $(d'_1, \ldots, d'_n)$ les droites de ces deux directions. Chaque point de $\Omega$ appartient à une unique $d_i$ et une unique $d'_j$. Réciproquement, $i$ et $j$ déterminent le point (on a vu que deux droites non parallèles s'intersectent en un unique point). On peut donc repérer les points de $\Omega$ par un couple $(i,j)$ d'entiers. Écrivons $p_{i,j} \in \Omega$ ce point d'intersection de $d_i$ et $d'_j$.
Numérotons maintenant les $(n-1)$ directions restantes : $$(\delta_{1, 1}, \ldots, \delta_{1, n}),\quad (\delta_{2, 1}, \ldots, \delta_{2, n}), \quad\ldots\quad (\delta_{n-1, 1}, \ldots, \delta_{n-1, n}).$$ Chacune de ces $n-1$ directions définit un tableau $n\times n$ : $T^{(1)}, \ldots, T^{(n-1)}$ rempli par les nombres de $1$ à $n$ : $T^{(r)}_{i,j}$ est l'unique entier $s$ tel que $p_{i,j}$ appartienne à la droite $\delta_{r,s}$.
Ces tableaux sont des carrés latins : si, par exemple, on voyait deux fois le même entier $s$ à la $i$-ième ligne du tableau $T^{(r)}$, cela signifierait que les droites $d_i$ et $\delta_{r,s}$ s'intersectent (au moins) deux fois, ce qui est exclu.
De même, ces carrés latins sont mutuellement orthogonaux : montrons-le pour $T^{(1)}$ et $T^{(2)}$ pour simplifier les notations. Soit $(s_1, s_2) \in \{1, \ldots, n\}^2$. Les deux droites $\delta_{1,s_1}$ et $\delta_{2,s_2}$ s'intersectent en un unique point $p_{i,j} \in \Omega$ (les deux droites ne sont pas parallèles). Alors, par définition, $T^{(1)}_{i,j} = s_1$ et $T^{(2)}_{i,j} = s_2$.
$$ T^{(1)} = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 3 & 1 \end{pmatrix} \qquad T^{(2)} = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{pmatrix}$$
Le théorème de Bose montre que le problème (difficile, on l'a vu) de l'existence de plans d'un ordre donné se traduit en termes de carrés latins mutuellement orthogonaux. Par exemple, le premier cas où l'on ne sait toujours pas dire s'il existe un plan d'ordre $n$ est le cas $n=12$. D'après le théorème de Bose, l'existence de ce plan est équivalente à celle de 11 carrés latins mutuellement orthogonaux. Le meilleur résultat dans cette direction date de 1961 : on sait qu'il existe cinq carrés latins d'ordre 12 mutuellement orthogonaux. On voit que les progrès sont lents !
De manière générale, le nombre maximal $N(n)$ de carrés latins d'ordre $n$ mutuellement orthogonaux reste très mystérieux, malgré de nombreuses recherches et une définition très élémentaire.