De nombreux théorèmes en mathématiques sont bien connus, d'autres sont insoupçonnés... Et pourtant beaucoup d'entre eux ne demandent que peu de connaissances mathématiques pour les comprendre. Partant de notions simples, notre objectif est de remettre au jour des théorèmes ignorés. Faisons un petit tour dans une branche bien connue: la géométrie.

La géométrie euclidienne1 est enseignée à des degrés d'approfondissement divers dès l'école primaire avec l'étude de quelques polygones. Nous allons commencer par l'un des théorèmes clés accessible à tout collégien : le cercle circonscrit à un triangle.

Considérons trois droites en position générale2. Ce système de droites forme un triangle non plat dans lequel chaque sommet est le point d’intersection d’une paire de droites. L’unique cercle passant par ces sommets est le cercle circonscrit à ce triangle. La construction est rappelée à la Figure 1.

Cercle circonscrit à un triangle

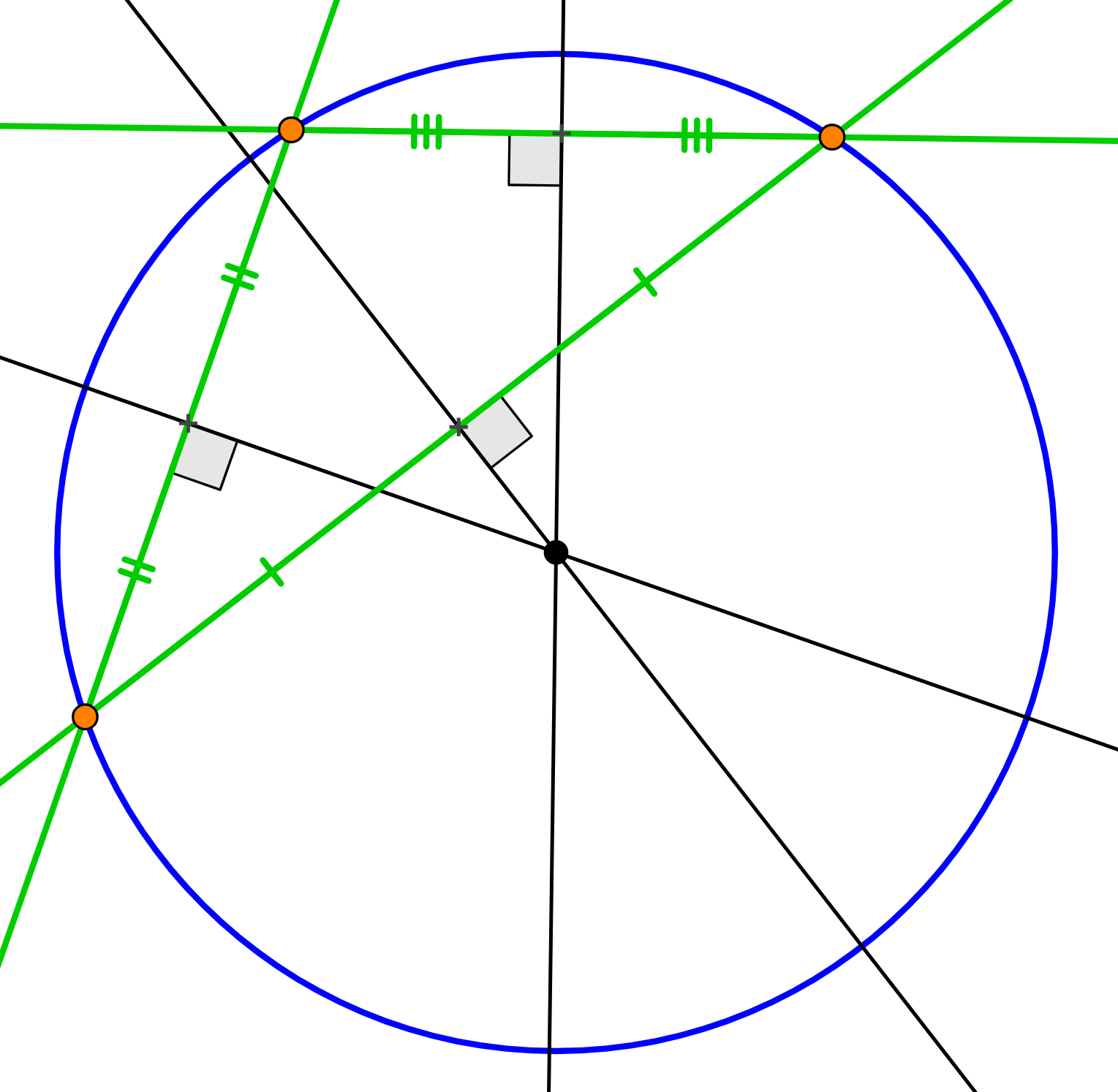
Les droites vertes, en position générale, forment un triangle dont les sommets sont les points oranges. Le cercle circonscrit à ce triangle est en bleu. Son centre est le point d'intersection des trois médiatrices en noir associées à chaque côté du triangle.

Complexifions la figure en considérant quatre droites en position générale, ainsi que les quatre cercles circonscrits associés à chaque triplet de droites. Une fois la construction finie, nous observons un résultat intrigant : les cercles sont concourants en un point. Voilà le théorème qui décrit cette configuration :

Théorème

(Point de Miquel)

Soit quatre droites en position générale dans le plan. Alors, les cercles circonscrits aux triangles formés par chaque triplet de droites sont concourants en un point, appelé point de Miquel.

Point de Miquel

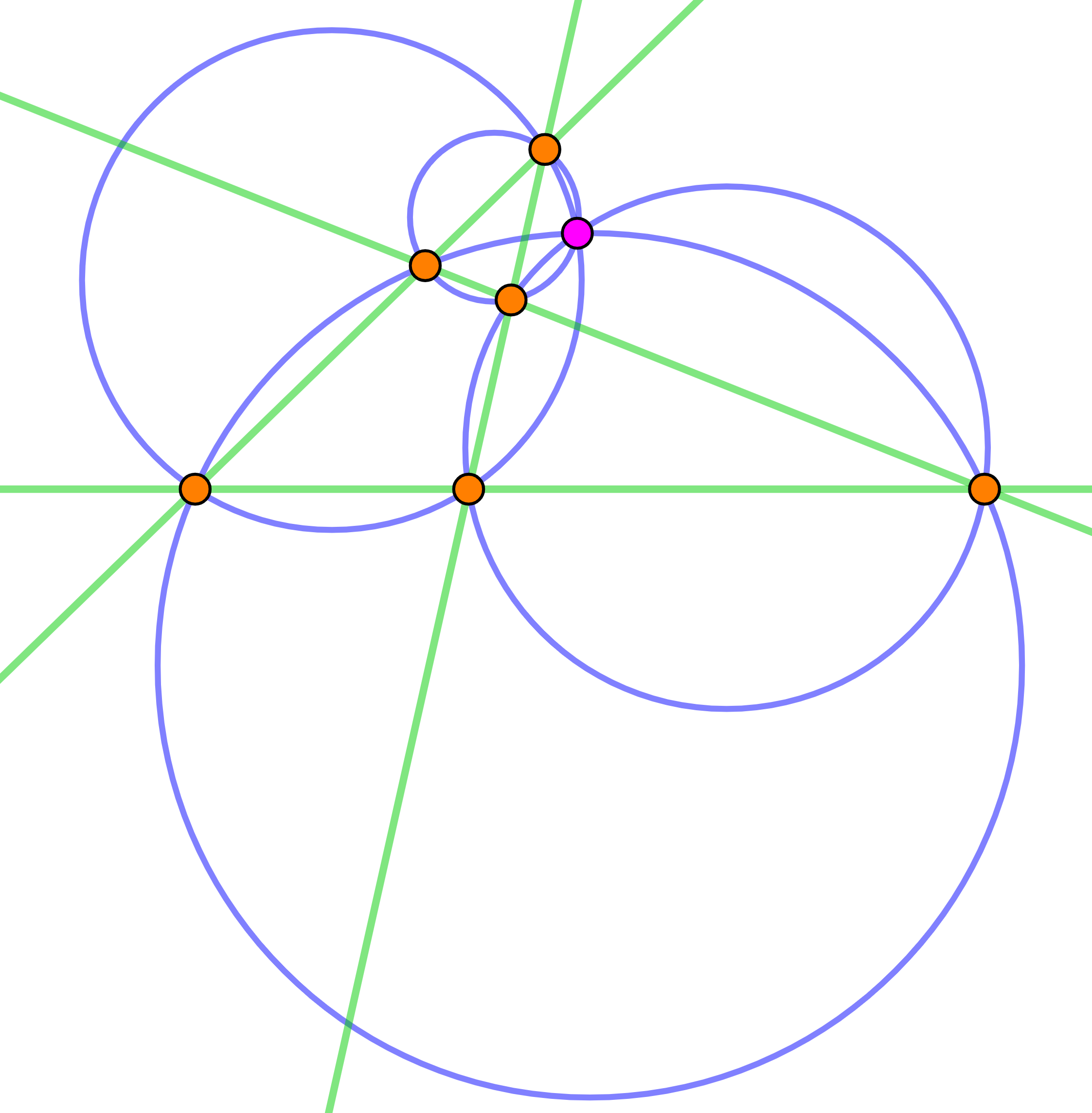
Les quatre droites vertes sont en position générale. Chacun des quatre triplets de droites forme un triangle qui possède un cercle circonscrit. Ces cercles circonscrits, en bleu, se coupent au point de Miquel en rose.

On pourra désormais dire qu'à un quadruplet de droites (en position générale), on associe un point de Miquel. Le théorème du point de Miquel peut se démontrer de plusieurs manières différentes. Une des démonstrations peut se faire à l'aide de la géométrie projective (3 page 348), une autre avec les angles orientés (4 page 243), mais il est intéressant de voir la démonstration classique faisant appel à la droite de Steiner 5.

Théorème

(Droite de Steiner)

Un point appartient au cercle circonscrit à un triangle si et seulement si les symétriques de ce point par rapport aux côtés du triangle sont alignés.
La droite passant par les symétriques d'un point se situant sur le cercle circonscrit à un triangle est appelée droite de Steiner de ce point.

Droite de Steiner

Le point rose est sur le cercle circonscrit orange au triangle formé par les droites vertes. Ainsi, d'après le théorème précédent, les trois symétriques du point rose par rapport aux côtés du triangle sont alignés. La droite rouge passant par ces points, est la droite de Steiner du point rose.

On admettra ce résultat dont une démonstration est donnée, par exemple, à la page 344 du livre 4. Grâce à cette droite, il devient assez simple de démontrer le théorème du point de Miquel. En voici une démonstration.

Démonstration (Point de Miquel) : Soient $d_1$, $d_2$, $d_3$ et $d_4$, quatre droites en position générale. On note $C_{1,2,3}$ le cercle circonscrit au triangle formé par les droites $d_1$, $d_2$ et $d_3$. De même, on note $C_{1,2,4}$, $C_{2,3,4}$ et $C_{1,3,4}$ les autres cercles circonscrits associés aux trois autres triplets de droites.
Considérons $C_{1,2,3}$ et $C_{1,2,4}$ et notons $M$ le point d'intersection de ces cercles qui n'est pas le point de concourt des droites $d_1$ et $d_2$6 (au besoin, voir l'ouvrage 7 page 59 pour plus de détails). Comme $M$ appartient au cercle circonscrit $C_{1,2,3}$, d'après le théorème de la droite de Steiner, les symétriques $M_1, M_2$ et $M_3$ du point $M$ par rapport aux droites $d_1$, $d_2$ et $d_3$ sont alignés. De même, comme $M$ appartient à $C_{1,2,4}$, les points $M_1, M_2$ et $M_4$ sont alignés. Ainsi, les points $M_1, M_2, M_3$ et $M_4$ sont alignés (sur la droite $(M_1M_2)$) 8.
Enfin, comme les points $M_1, M_3, M_4$ et $M_2, M_3, M_4$ sont alignés, par le théorème de la droite de Steiner, on en déduit que le point $M$ appartient également aux cercles $C_{1,3,4}$ et $C_{2,3,4}$. Donc $M$ appartient aux quatre cercles circonscrits.

Alignement des symétriques

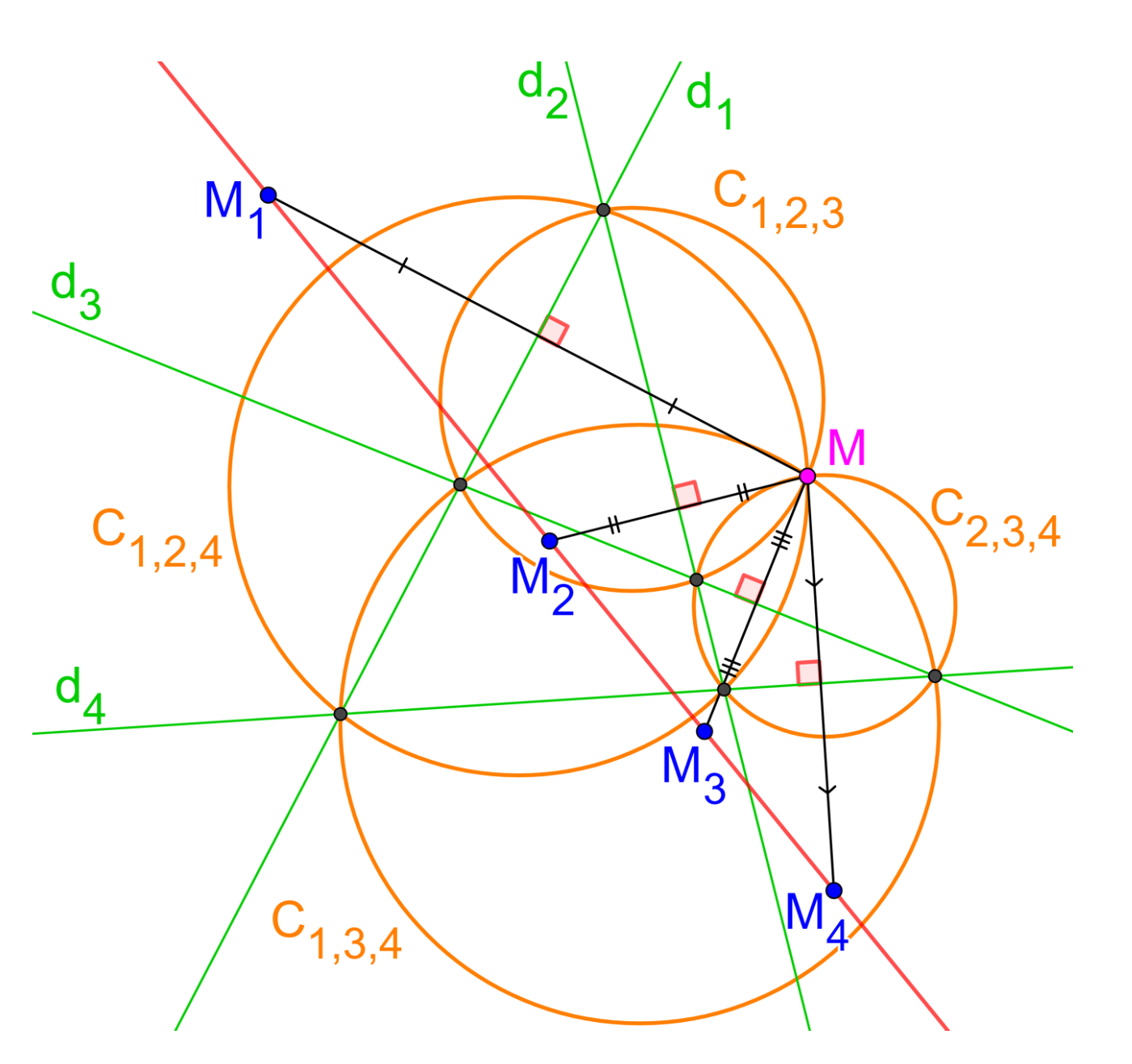
Cette figure complète la Figure 2 en ajoutant les symétriques $M_1,M_2,M_3$ et $M_4$ par rapport aux droites $d_1,d_2,d_3$ et $d_4$ respectivement. L'alignement des points $M_1,M_2,M_3$ et $M_4$ est la clé de voûte pour démontrer que les quatre cercles circonscrits sont concourants en un point.

Continuons notre périple géométrique en compliquant légèrement la figure. Nous savons déjà qu'avec trois droites en position générale, on peut former un triangle et son cercle circonscrit. Nous venons de voir qu'en rajoutant une droite à ce système, il existait alors quatre cercles concourants en un point : le Point de Miquel. En ajoutant une cinquième droite au système, nous allons construire un cercle particulier (ou une droite particulière) associé à ces droites : le cercle-droite de Miquel.

Avec cinq droites, il est possible de faire cinq groupes de quatre droites (un quadruplet de droites s'obtient en retirant une droite et il y a cinq façons possibles de retirer une droite parmi les cinq). Dans un système de cinq droites, il y a donc cinq points de Miquel, chacun associé à un quadruplet de droites.

Théorème

(Cercle-droite9 de Miquel)

Pour cinq droites en position générale dans le plan, les cinq points de Miquel associés aux cinq quadruplets de droites, sont cocycliques, alignés ou confondus.

Cercle-droite de Miquel

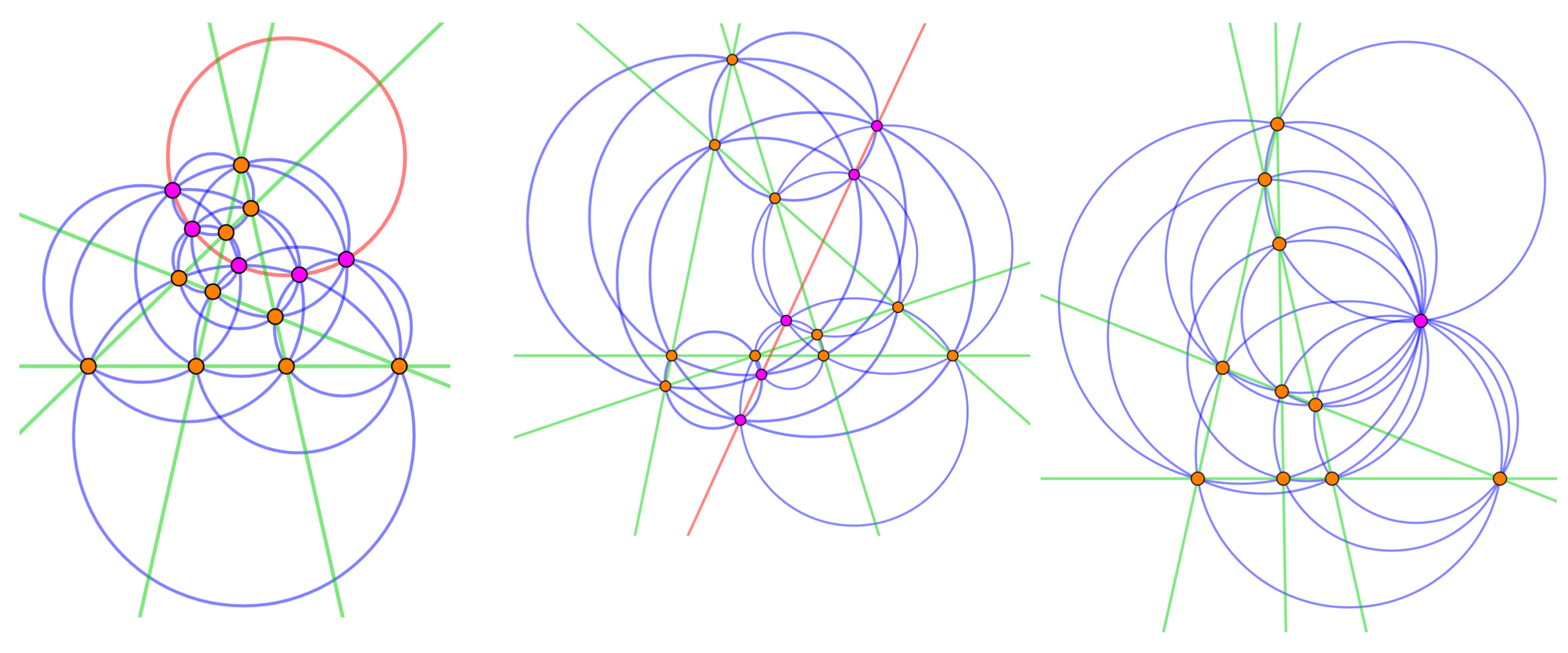
Les trois figures montrent tous les éléments nécessaires pour la construction du cercle-droite de Miquel (en rouge). Les cinq droites en position générale (en vert), les points d'intersection associés aux dix ($\binom{5}{2}=10$) paires de droites (en orange), les cercles circonscrits associés aux dix ($\binom{5}{3}=10$) triplets de droites (en bleu), les points de Miquel associés aux cinq ($\binom{5}{4}=5$) quadruplets de droites (en rose). Finalement, le cercle-droite de Miquel peut être un cercle (image de gauche), une droite (image du milieu) ou bien un point lorsque les cinq points de Miquel sont confondu (image de droite).

Ainsi, à partir de cinq droites, on construit dix $(\binom{5}{3}=10)$ cercles circonscrits aux dix triangles formés par ces droites. De cette construction découle cinq $(\binom{5}{4}=5)$ points de Miquel, cocyliques, alignés ou confondus ! Voici une élégante illustration de la beauté de la géométrie classique.

Ensuite de la même manière, à partir de six droites, on construit six $(\binom{6}{5}=6)$ cercles-droites de Miquel et ces cercles-droites sont concourants : c'est le point d'orgue de cette symphonie des cercles circonscrits.

Théorème

(Point de Clifford)

Pour six droites en position générale, les six cercles-droites de Miquel associés aux six quintuplets de droites sont concourants en un point.

Point de Clifford

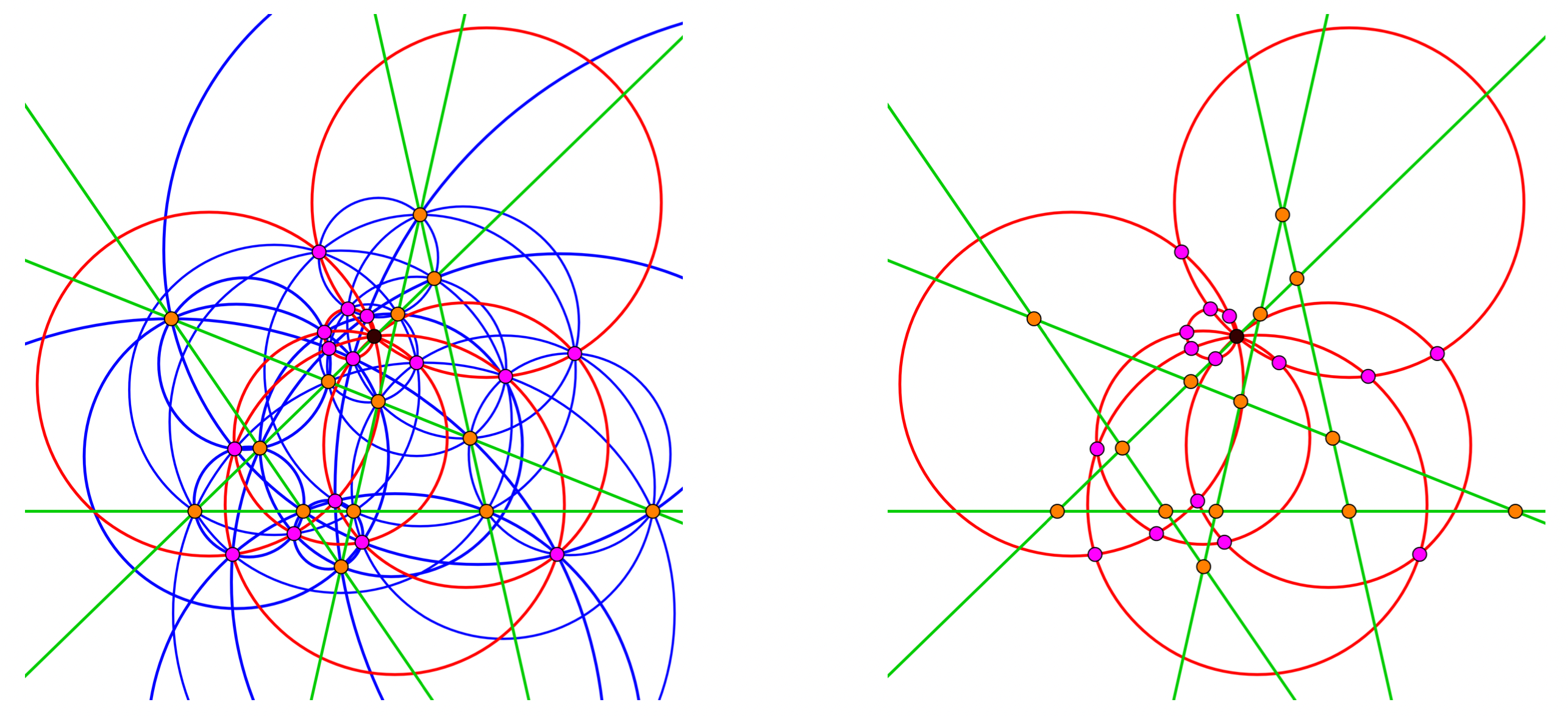
La figure de gauche montre tous les éléments nécessaires pour la construction du point de Clifford (en noir). Les six droites en position générale (en vert), les points d'intersection associés aux quinze ($\binom{6}{2}=15$) paires de droites (en orange), les cercles circonscrits associés aux vingt ($\binom{6}{3}=20$) triplets de droites (en bleu), les points de Miquel associés aux quinze ($\binom{6}{4}=15$) quadruplets de droites (en rose) et les cercle-droites de Miquel associés aux six ($\binom{6}{5}=6$) quintuplets de droites (en rouge). Finalement, le point de Clifford est le point d'intersection des cercles-droites de Miquel. La figure de droite est plus synthétique : il n'y a pas les cercles circonscrits. On remarque que les cercle-droites de Miquel s'intersectent tous au point noir.

En annexe, nous donnons la preuve du théorème qui établit l'existence du cercle-droite de Miquel. En revanche, cette symphonie des cercles et des points reste inachevée. Nous ne donnerons pas la preuve du théorème sur le point de Clifford, cette démonstration est trop technique pour cet article et nécessite d'introduire la géométrie dite inversive. Pour cette géométrie, les droites sont des cercles particuliers, ainsi l'alignement et la cocyclicité sont des notions équivalentes.

Nous achèverons cette symphonie des cercles circonscrits dans un futur article. Dans celui-ci, nous introduirons la notion de point central qui généralise le point de Miquel pour $n=4$ droites et le point de Clifford pour $n=6$ droites à un nombre pair de droites en position générale. Nous introduirons également la notion de cercle-droite central qui généralise le cercle circonscrit pour $n=3$ droites et le cercle-droite de Miquel pour $n=5$ droites à un nombre impair de droites en position générale. Le lecteur curieux et impatient peut néanmoins consulter le livre de Boyer 3 pages 348 à 350 et regarder la vidéo donnée au lien suivant https://cutt.ly/638sBhY.

Annexe

Pour démontrer le cas de cinq droites, les choses deviennent un peu plus compliquées.

Un objet essentiel en géométrie est le birapport que l'on définit à travers le théorème suivant qui était au programme de troisième il y a quelques années :

Théorème

(Angle au centre)

Soit $\mathscr{C}$ un cercle de centre $ \Omega$, et $A$ et $B$ deux points de $\mathscr{C}$ distincts. Si un point $M$ du plan appartient au cercle $\mathscr{C}$, alors \[2\mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB}) = \mathrm{mes}(\overrightarrow{\Omega A},\overrightarrow{\Omega B})\mod 2\pi \] où $\mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB})$ désigne une mesure de l'angle orienté $(\overrightarrow{MA},\overrightarrow{MB})$ en radians.

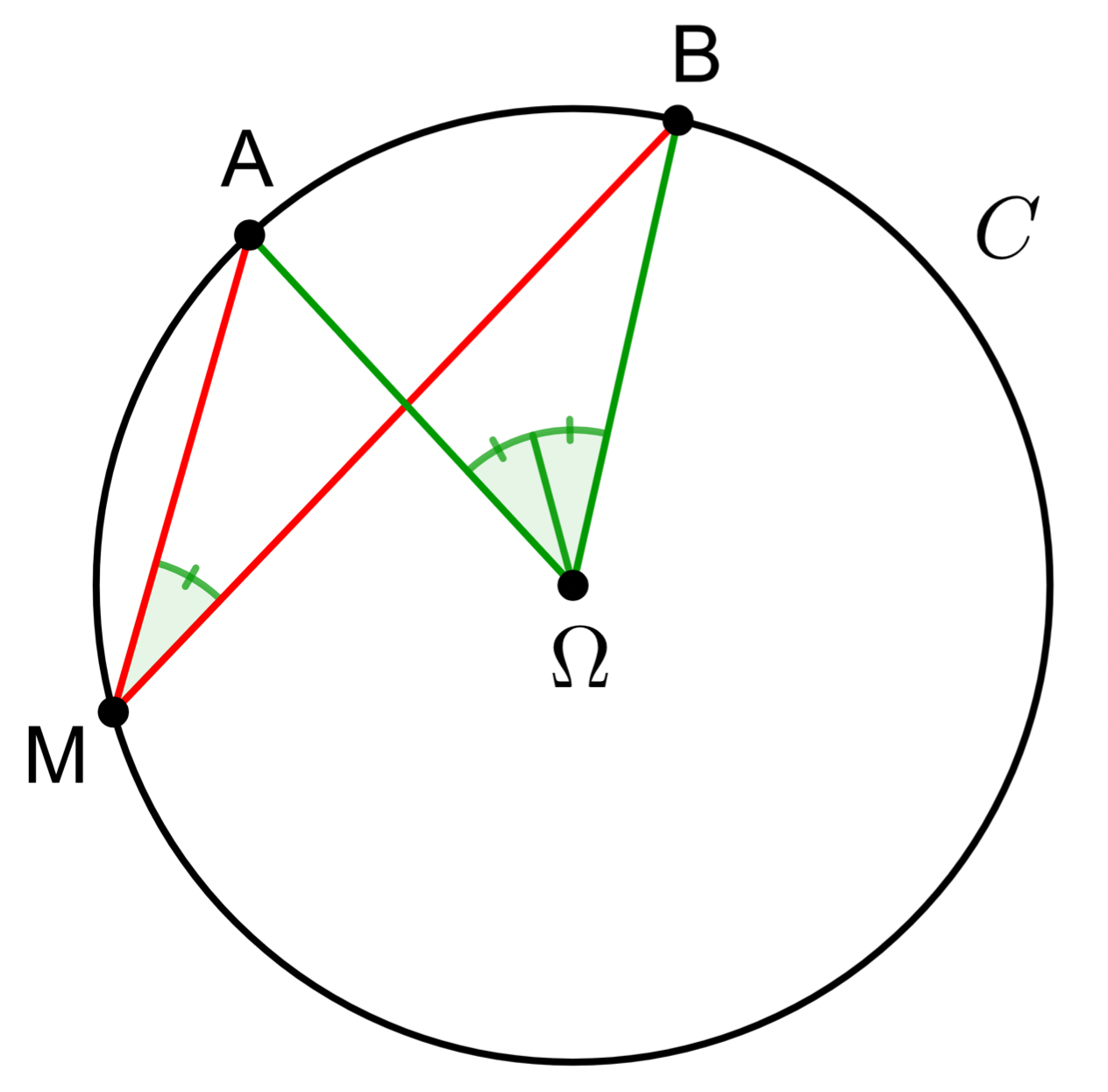
De ce théorème découle un résultat très fort : le théorème de l'angle inscrit.

Théorème

(Angle inscrit)

Soit $\mathscr{C}$ un cercle de centre $ \Omega$, $A$ et $B$ deux points distincts de $\mathscr{C}$. Si $M$ et $N$ sont deux points de $\mathscr{C}\backslash\{A,B\}$ alors \begin{align*} \mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB})=\mathrm{mes}(\overrightarrow{NA},\overrightarrow{NB})\mod \pi \end{align*}

En effet, d'après le théorème de l'angle au centre, on a :

\begin{align*} 2\mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB}) = \mathrm{mes}(\overrightarrow{\Omega A},\overrightarrow{\Omega B})\mod 2\pi.\\ 2\mathrm{mes}(\overrightarrow{NA},\overrightarrow{NB}) = \mathrm{mes}(\overrightarrow{\Omega A},\overrightarrow{\Omega B})\mod 2\pi. \end{align*} D'où : \begin{align*} \mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB})=\mathrm{mes}(\overrightarrow{NA},\overrightarrow{NB})\mod \pi. \end{align*}

Si on se place dans le plan complexe $\mathbb{C}$ et que l'on note $a, b, m$ et $n$ les affixes respectives des points $A, B, M$ et $N$, comme les points $M$ et $N$ sont bien distincts de $A$ et de $B$, on peut écrire : \begin{align}\label{formule1.1} &\mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB})=\mathrm{mes}(\overrightarrow{NA},\overrightarrow{NB})\mod \pi \\ \Longleftrightarrow & arg\left(\dfrac {m-a}{m-b} \right) = arg\left( \dfrac{n-a}{n-b} \right)\mod \pi\notag\\ \Longleftrightarrow & \dfrac {m-a}{m-b}\times\dfrac {n-b}{n-a} \in \mathbb{R}^*. \end{align}

La quantité $[A,B,M,N]$ définie par $[A,B,M,N]=\dfrac {m-a}{m-b}\times\dfrac {n-b}{n-a}$ s'appelle le birapport des quatre points $A$, $B$, $M$ et $N$.

Remarque

Si deux points $M(m)$ et $ N(n)$ de $\mathbb{C}$ appartiennent à la droite $(AB)$ et sont distincts de $A(a)$ et de $B(b)$, alors $\mathrm{mes}(\overrightarrow{MA},\overrightarrow{MB})=\mathrm{mes}(\overrightarrow{NA},\overrightarrow{NB})\mod \pi$, donc le birapport $[A,B,M,N]$ est réel.

☞ Autrement dit, si quatre points distincts sont sur un même cercle ou une même droite, alors leur birapport est réel.

 

La réciproque est également vraie. Elle se démontre à l'aide du théorème de l'angle au centre et du théorème de l'angle de la tangente (qui est un cas limite du théorème de l'angle au centre).

☞ Par la suite, nous utiliserons le résultat suivant :

Le birapport $\big[A,B,C,D\big]$ de quatre points distincts $A, B, C$ et $D$, est réel si et seulement si les points $A, B, C$ et $D$ sont cocycliques ou alignés.

Avant de démontrer le théorème du cercle-droite de Miquel, nous devons faire appel à un théorème qui nous sera nécessaire pour la suite.

Théorème

(Six cercles)

Soit $\mathcal{C}_1, \mathcal{C}_2, \mathcal{C}_3$ et $\mathcal{C}_4$ quatre cercles tels que :

  • $\mathcal{C}_1$ et $\mathcal{C}_2$ s'intersectent en deux points distincts $A_1$ et $B_1$ ;
  • $\mathcal{C}_2$ et $\mathcal{C}_3$ s'intersectent en deux points distincts $A_2$ et $B_2$ ;
  • $\mathcal{C}_3$ et $\mathcal{C}_4$ s'intersectent en deux points distincts $A_3$ et $B_3$ ;
  • $\mathcal{C}_4$ et $\mathcal{C}_1$ s'intersectent en deux points distincts $A_4$ et $B_4$.

Si les points $A_1, A_2, A_3$ et $A_4$ sont distincts et cocycliques (ou alignés), alors $B_1, B_2, B_3, B_4$ sont cocycliques (ou alignés).

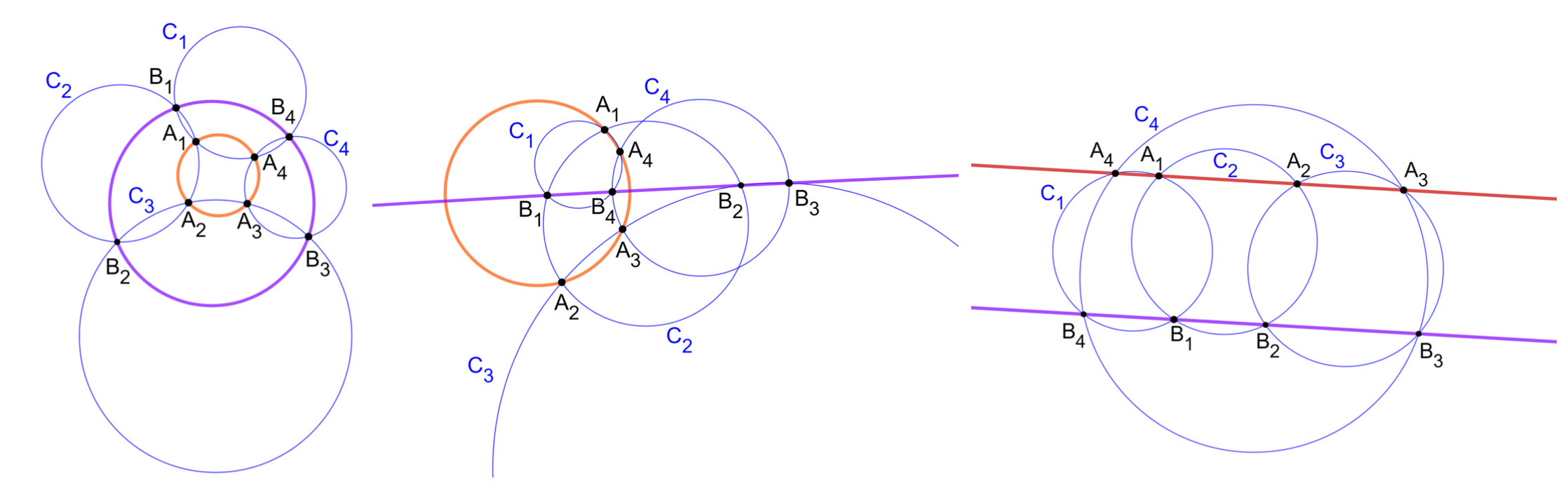
Les trois cas possibles du théorème des six cercles

Premier cas (à gauche) : les deux quadruplets $A_1, A_2, A_3, A_4$ et $B_1, B_2, B_3, B_4$ sont cocycliques. Deuxième cas (au centre) : l'un des quadruplets a des points cocycliques et l'autre quadruplet a des points alignés. Troisième cas (à droite) : les deux quadruplets $A_1, A_2, A_3, A_4$ et $B_1, B_2, B_3, B_4$ ont leurs points alignés.

Ce théorème se montre facilement avec le birapport.

Comme $A_1, B_1, A_4$ et $B_4$ sont sur $\mathcal{C}_1$, $\color{blue}{[A_1,B_4,A_4,B_1]}$ est réel. De même pour: \[\color{red}{[A_2,B_1,A_1,B_2]},\quad [A_3,B_2,A_2,B_3],\quad \color{green}{[A_4,B_3,A_3,B_4]}\quad\text{ sur $\mathcal{C}_2$, $\mathcal{C}_3$, $\mathcal{C}_4$ respectivement.} \] Ainsi, le rapport $W =\frac{\color{red}{[A_2,B_1,A_1,B_2]}\times\color{green}{[A_4,B_3,A_3,B_4]}}{[A_3,B_2,A_2,B_3]\times \color{blue}{[A_1,B_4,A_4,B_1]}}\quad\text{est réel.}$

Par un simple calcul, on a: $W =[A_1,A_3,A_2,A_4]\times[B_2,B_4,B_1,B_3] $ réel.

Par conséquent, si $A_1, A_2, A_3$ et $A_4$ sont cocycliques ou alignés, $[A_1,A_3,A_2,A_4]$ est réel, et donc $[B_2,B_4,B_1,B_3]$ l'est aussi. Ainsi $B_1, B_3, B_2$ et $B_4$ sont cocycliques ou alignés.

☞ Maintenant, nous avons tous les outils nécessaires pour démontrer l'existence du cercle-droite de Miquel.

Théorème

(Cercle-droite de Miquel)

Pour cinq droites en position générale dans le plan, les cinq points de Miquel associés aux cinq quadruplets de droites sont cocycliques ou alignés.

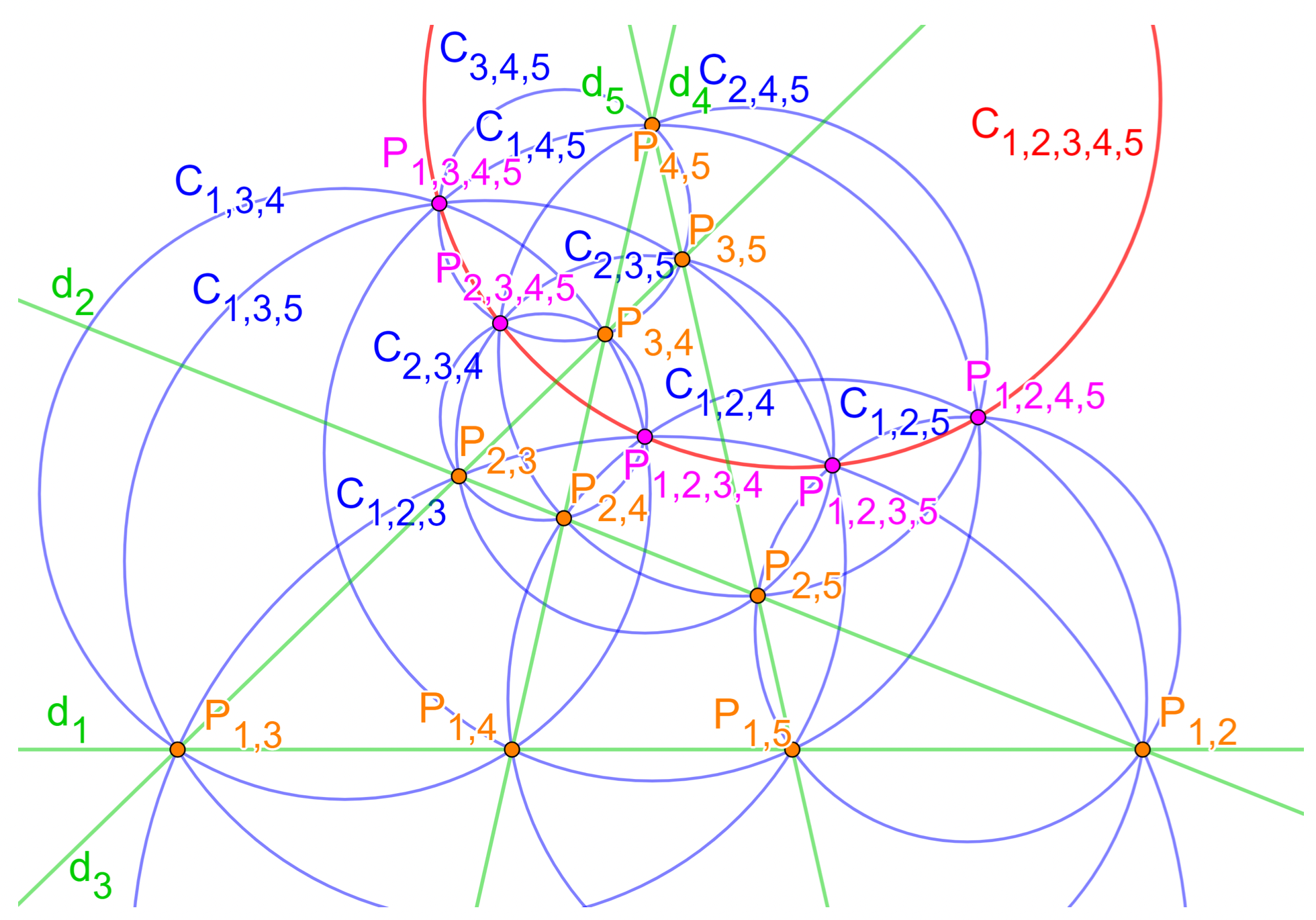
Démonstration : cercle-droite de Miquel Pour cinq droites: $d_1$, $d_2$, $d_3$, $d_4$ et $d_5$ en position générale :

  • On note $P_{i,j}$ le point d'intersection des deux droites $d_i$ et $d_j$.
  • On rappelle que $C_{i,j,k}$ est le cercle circonscrit au triangle dont les sommets sont $P_{i,j}$, $P_{i,k}$ et $P_{j,k}$.
  • On note $P_{i,j,k,l}$ le point de Miquel déterminé par les droites $d_i, d_j, d_k$ et $d_l$; autrement dit, le point d'intersection des cercles $C_{j,k,l}, C_{i,k,l}, C_{i,j,l},C_{i,j,k}$. Exemple: on note $P_{1,2,3,4}$ le point de Miquel construit à partir des quatre droites $d_1, d_2, d_3$ et $d_4$. Il y a cinq points de Miquel.
Illustration des notations appliquées à la démonstration du théorème du cercle-droite de Miquel.

Cas 1 : Au moins deux points de Miquel sont confondus.

Dans le cas où deux points de Miquel sont confondus, par exemple $P_{1,2,3,4}$ et $P_{2,3,4,5}$, les sept cercles circonscrits $C_{1,2,3}, C_{2,3,4}, C_{1,3,4}, C_{1,2,4}, C_{3,4,5}, C_{2,4,5}$ et $C_{2,3,5}$, permettant de construire ces deux points de Miquel, sont concourants en un point.

D'après la note 4, les deux points de Miquel $P_{1,2,3,4}$ et $P_{2,3,4,5}$ sont distincts des points $P_{3,4}$, $P_{2,4}$ et $P_{2,3}$. Comme :

  • $C_{1,3,4}$ et $C_{3,4,5}$ s'intersectent aussi en $P_{1,3,4,5}$ et $P_{3,4}$;
  • $C_{1,2,4}$ et $C_{2,4,5}$ s'intersectent aussi en $P_{1,2,4,5}$ et $P_{2,4}$;
  • $C_{1,2,3}$ et $C_{2,3,5}$ s'intersectent aussi en $P_{1,2,3,5}$ et $P_{2,3}$;

On en déduit que les cinq points de Miquel sont confondus. Ainsi, ils sont situés sur un cercle réduit en un point.

Cas 2 : Les points de Miquel sont distincts deux à deux.

On veut montrer que cinq droites déterminent un cercle-droite de Miquel, ce qui revient à montrer que $P_{1,2,3,4}, P_{2,3,4,5}, P_{1,3,4,5}, P_{1,2,4,5}$ et $P_{1,2,3,5}$ sont cocycliques ou alignés. Comme les cinq points de Miquel et les points d'intersection des droites $d_i$ sont tous deux à deux distincts, nous allons pouvoir utiliser le théorème des six cercles.

Montrons la cocyclicité ou l'alignement des points $P_{1,2,3,4}$, $P_{2,3,4,5}$, $P_{1,3,4,5}$ et $P_{1,2,4,5}$ : Considérons les quatre cercles $C_{1,2,3}$, $C_{1,2,4}$, $C_{1,3,4}$ et $C_{2,3,4}$.

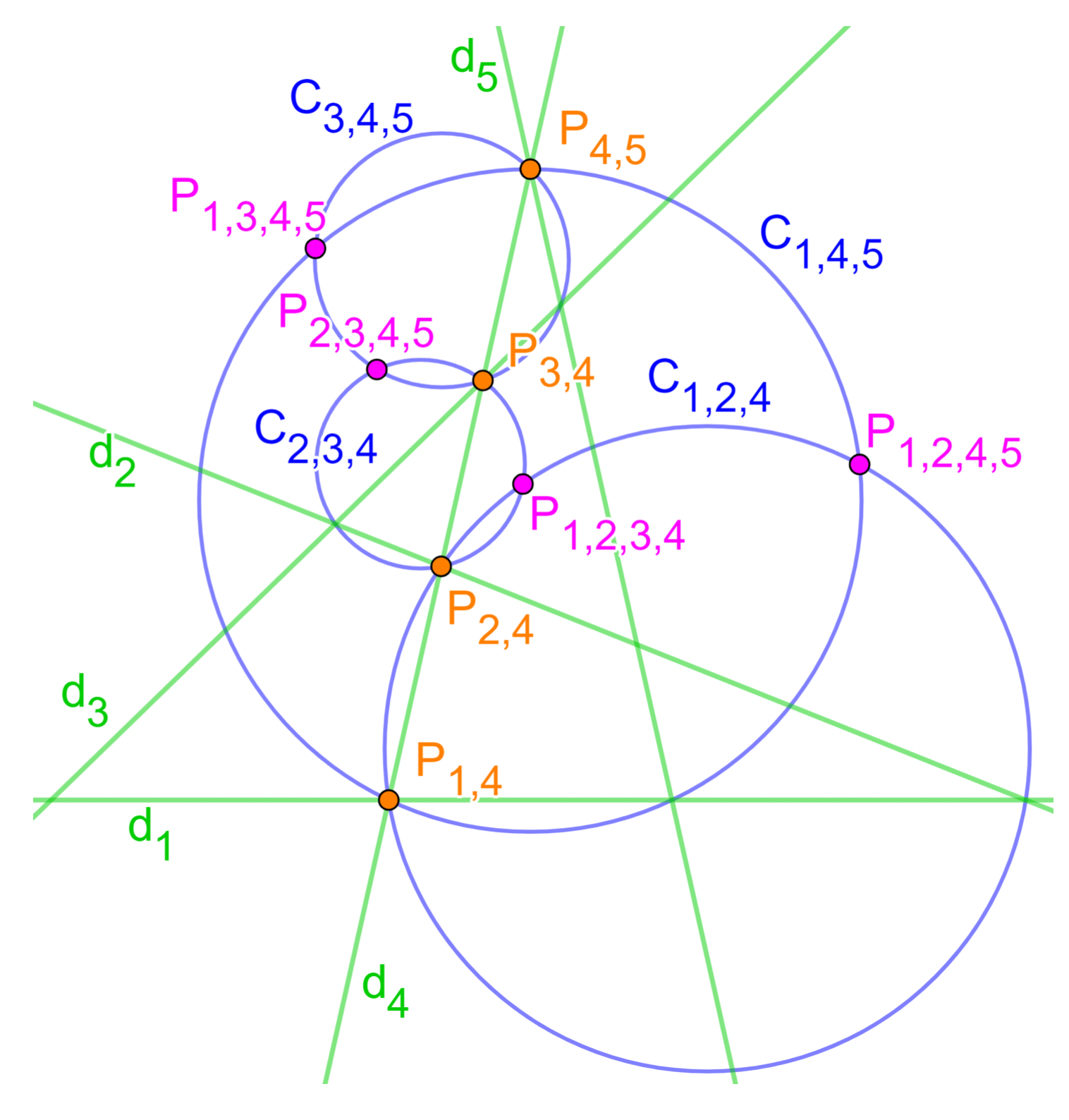
  • $C_{1,2,4}$ et $C_{2,3,4}$ s'intersectent en $P_{1,2,3,4}$ et $P_{2,4}$;
  • $C_{2,3,4}$ et $C_{3,4,5}$ s'intersectent en $P_{2,3,4,5}$ et $P_{3,4}$;
  • $C_{3,4,5}$ et $C_{1,4,5}$ s'intersectent en $P_{1,3,4,5}$ et $P_{4,5}$;
  • $C_{1,4,5}$ et $C_{1,2,4}$ s'intersectent en $P_{1,2,4,5}$ et $P_{1,4}$.

Or $P_{2,4}$, $P_{3,4}$, $P_{4,5}$ et $P_{1,4}$ appartiennent à $d_{4}$, donc en vertu du théorème des six cercles, les quatre points $P_{1,2,3,4}$, $P_{2,3,4,5}$ $P_{1,3,4,5}$ et $P_{1,2,4,5}$ sont cocycliques ou alignés.

Les mêmes arguments s'appliquent aux quatre points $P_{2,3,4,5}$, $P_{1,3,4,5}$, $P_{1,2,4,5}$ et $P_{1,2,3,5}$ qui sont donc également cocycliques ou alignés.

Alignement ou cocyclicité

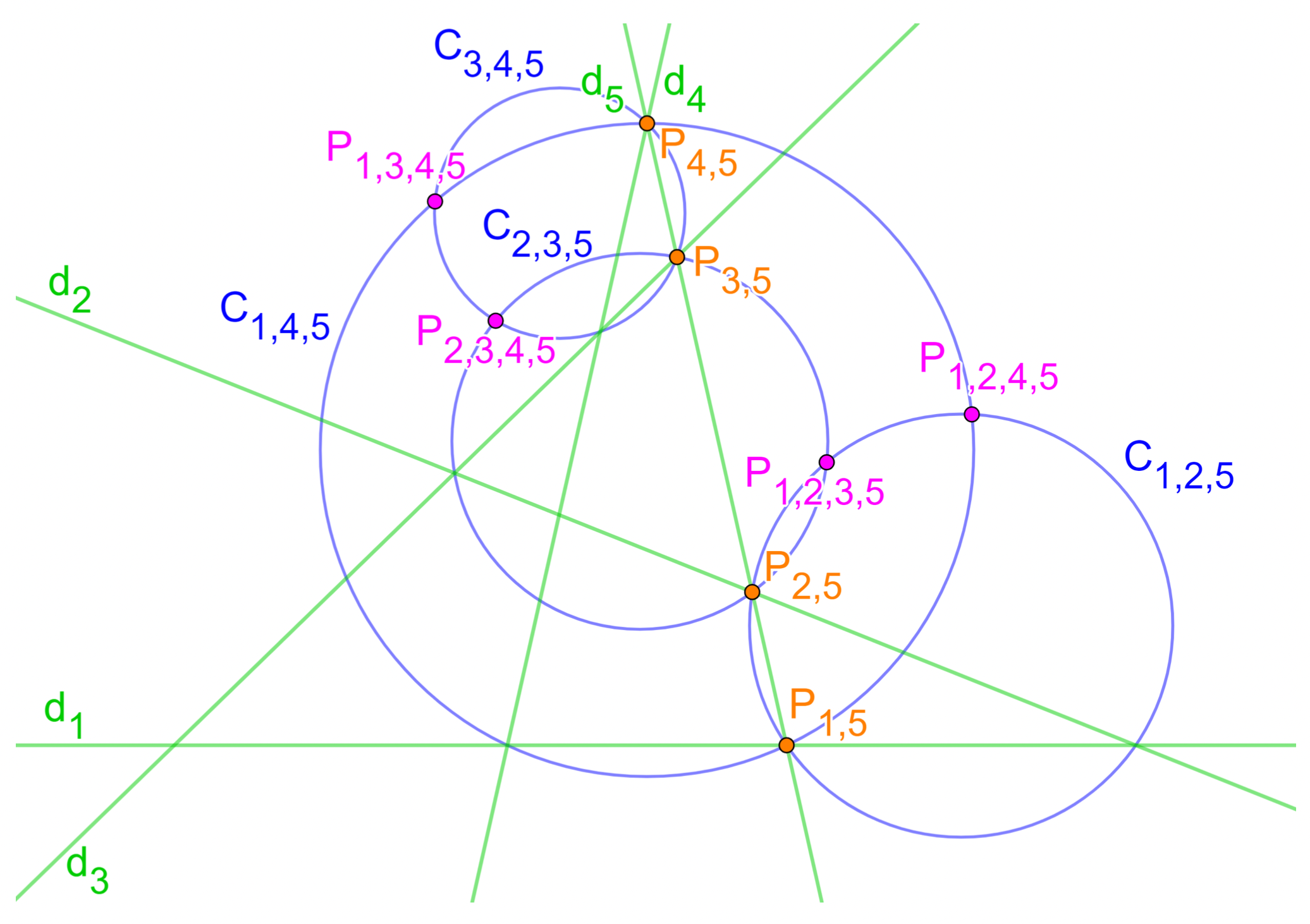
Cette figure montre les éléments géométriques utiles pour établir l'alignement ou la cocyclicité des points de Miquel $P_{2,3,4,5}$, $P_{1,3,4,5}, P_{1,2,4,5}$ et $P_{1,2,3,5}$. En effet, par construction les points $P_{1,5}, P_{2,5}, P_{3,5}$ et $P_{4,5}$ sont sur la droite $d_5$ donc, d'après le théorème des six cercles, les points $P_{2,3,4,5}$, $P_{1,3,4,5}, P_{1,2,4,5}$ et $P_{1,2,3,5}$ sont cocycliques ou alignés.

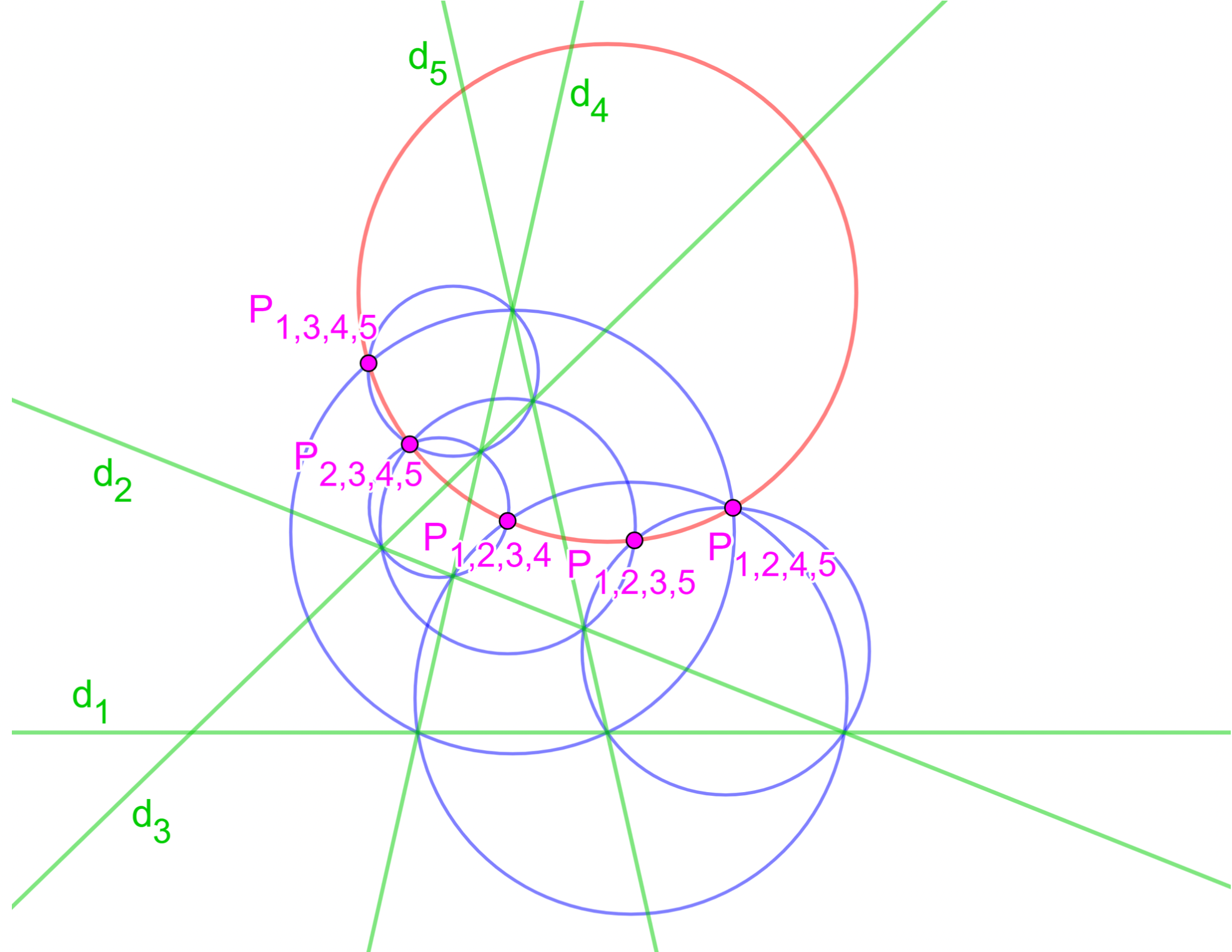
Ainsi $P_{1,2,3,4}$, $P_{2,3,4,5}$, $P_{1,3,4,5}$ et $P_{1,2,4,5}$ sont cocycliques ou alignés, de même que $P_{2,3,4,5}$, $P_{1,3,4,5}$, $P_{1,2,4,5}$ et $P_{1,2,3,5}$. Or les trois points, $P_{2,3,4,5}$, $P_{1,3,4,5}$ et $P_{1,2,4,5}$ sont en commun dans les deux quadruplets; on en déduit que les cinq points de Miquel $P_{1,2,3,4}$, $P_{2,3,4,5}$, $P_{1,3,4,5}$, $P_{1,2,4,5}$ et $P_{1,2,3,5}$ sont tous cocycliques ou alignés.

En superposant les figures 8 et 9 on observe que les cinq points de Miquel sont cocycliques ou alignés.

Travaux pratiques : Caractérisation des points appartenant au cercle circonscrit d'un triangle

  1. Sur GeoGebra, construire un triangle $ABC$ et son cercle circonscrit $\mathcal{C}_{ABC}$. Placer un point $M$ sur $\mathcal{C}_{ABC}$ puis construire $M'_{(AB)}, M'_{(AC)}$ et $M'_{(BC)}$ les symétriques de $M$ par rapport aux droites $(AB), (AC)$ et $(BC)$. Déplacer le point $M$ sur le cercle $\mathcal{C}_{ABC}$. Que remarque-t-on ? Énoncer une propriété qui traduit cette expérience numérique.
  2. Dans une nouvelle fenêtre, construire un triangle $ABC$ et son cercle circonscrit $\mathcal{C}_{ABC}$. Placer à présent un point $N$ hors du cercle $\mathcal{C}_{ABC}$ puis construire $N'_{(AB)}, N'_{(AC)}$ et $N'_{(BC)}$ les symétriques de $N$ par rapport aux droites $(AB), (AC)$ et $(BC)$. Déplacer le point $N$. Quelle différence observe-t-on par rapport à la question 1 ? Énoncer une propriété qui traduit cette expérience numérique.

Travail d'approfondissement : Cercles circonscrits et point de Miquel Durant les travaux pratiques nous avons montré les propriétés suivantes :

Propriété

 

Soit $ABC$ un triangle non plat et $\mathcal{C}_{ABC}$ son cercle circonscrit. Si $M\in \mathcal{C}_{ABC}$ alors les symétriques $M'_{(AB)}, M'_{(AC)}$ et $M'_{(BC)}$ de $M$ par rapport aux droites $(AB), (AC)$ et $(BC)$ sont alignés.

Propriété

 

Soit $ABC$ un triangle non plat, $\mathcal{C}_{ABC}$ son cercle circonscrit, $M$ un point du plan et $M'_{(AB)}, M'_{(AC)}$ et $M'_{(BC)}$ de $M$ les symétriques du point $M$ par rapport aux droites $(AB), (AC)$ et $(BC)$. Si $M'_{(AB)}, M'_{(AC)}$ et $M'_{(BC)}$ sont alignés alors $M$ est un point du cercle circonscrit $\mathcal{C}_{ABC}$.

On considère 4 droites en position quelconque. Ces droites délimitent 4 triangles : EAD, EBC, FDC, FAB.

  1. Sur la figure 1 construire :
    • les cercles circonscrits $\mathcal{C}_{EAD}$ et $\mathcal{C}_{FDC}$ aux triangles EAD et FDC. On pose $M$ le point d'intersection de $\mathcal{C}_{EAD}$ et $\mathcal{C}_{FDC}$ qui n'appartient à aucune des 4 droites;
    • les points $M'_{(AB)}, M'_{(BC)}$ et $M'_{(CD)}$ et $M'_{(DA)}$ symétriques du point $M$ par rapport aux droites $(AB), (BC), (CD)$ et $(DA)$.
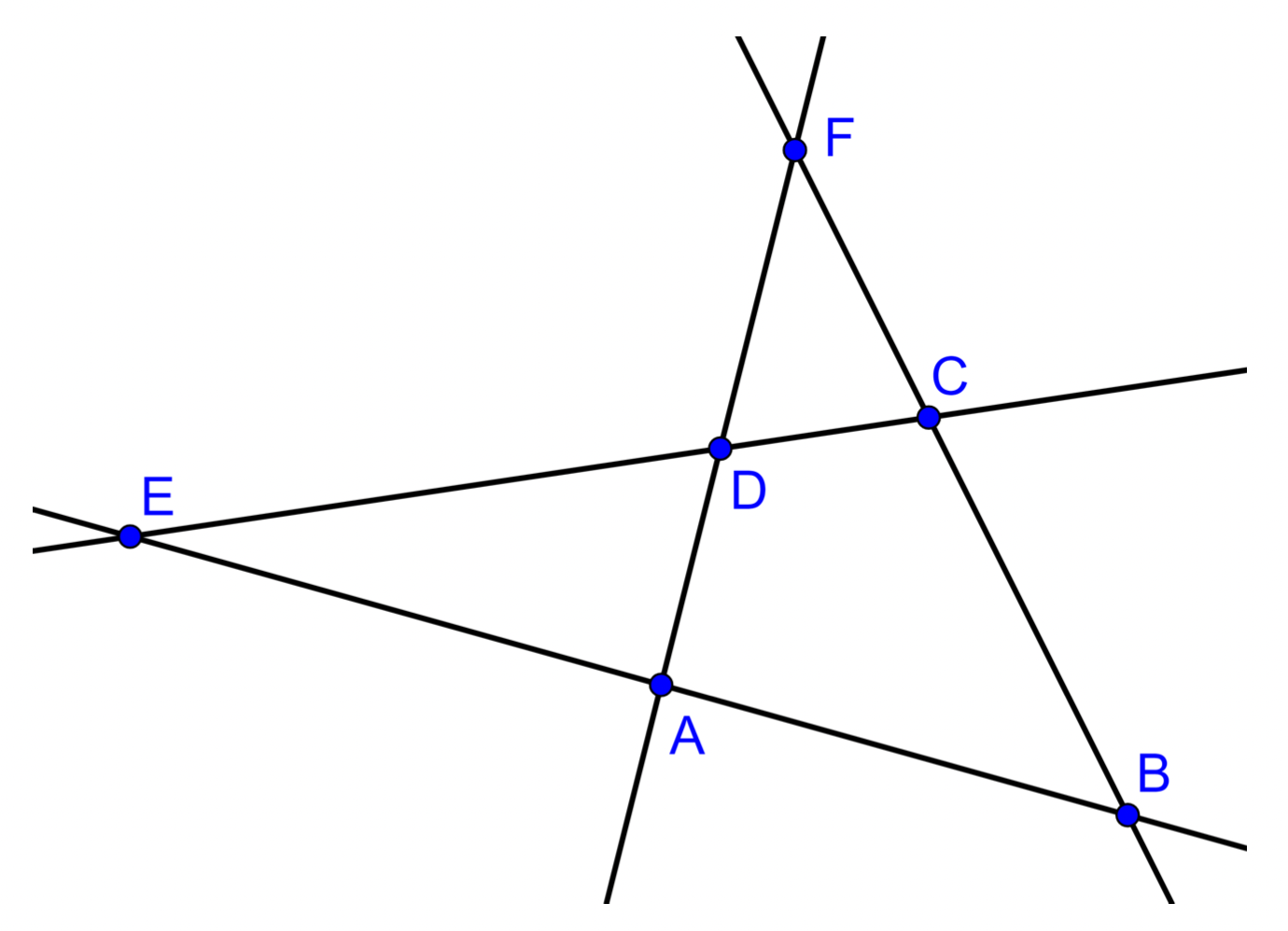
  2. En utilisant la propriété 10, montrer que les points $M'_{(AB)}, M'_{(BC)}$ et $M'_{(CD)}$ et $M'_{(DA)}$ sont alignés.
  3. On note $\mathcal{C}_{EBC}$ le cercle circonscrits aux triangles EBC. En utilisant la propriété 2, montrer que le point $M$ appartient à $\mathcal{C}_{EBC}$. 10
  4. Sur la figure 2 construire : les cercles circonscrits $\mathcal{C}_{EAD}, \mathcal{C}_{FDC}, \mathcal{C}_{EBC}$ et $\mathcal{C}_{FAB}$ aux triangles EAD, FDC, EBC et FAB.
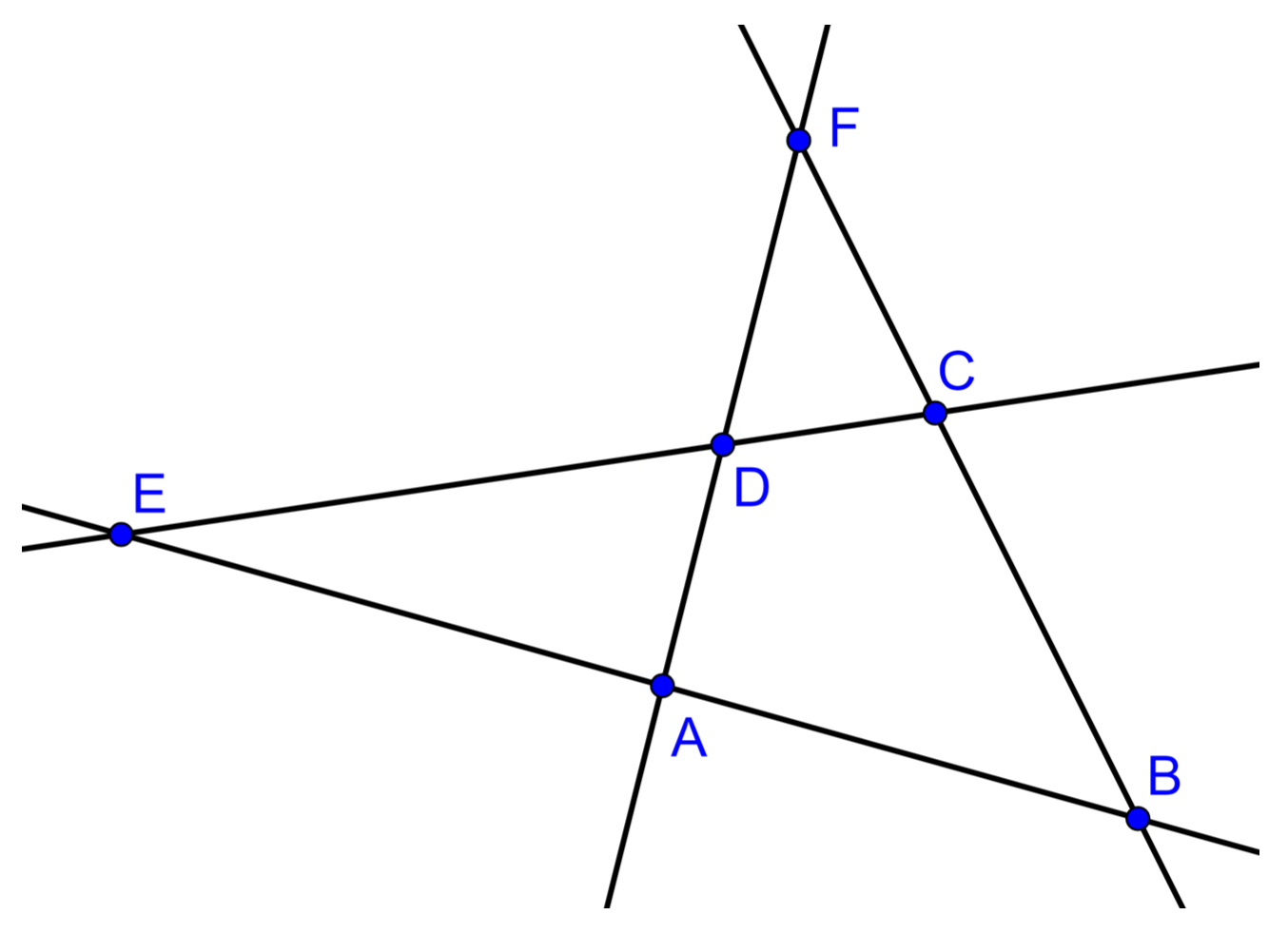
  5. Que peut-on dire des cercles $\mathcal{C}_{EAD}, \mathcal{C}_{FDC}, \mathcal{C}_{EBC}$ et $\mathcal{C}_{FAB}$ ? Justifier en utilisant les questions précédentes.