Après plus de 80 ans d'efforts et de résultats partiels, une conjecture sur l’approximation des nombres irrationnels enfin prouvée !
L’été dernier, un pas important a été franchi dans la compréhension des méthodes d’approximation des nombres irrationnels par des fractions.
Les irrationnels s’écrivent avec une infinité de chiffres après la virgule et on ne maîtrise plus grand-chose une fois cette virgule franchie :
$$\pi = 3,14159265358979\dots ,$$
$$\sqrt{2}= 1,414213562373095048 \dots ,$$
et on pourrait remplir une infinité de pages de décimales !
Depuis longtemps on s’intéresse à ces nombres irrationnels et aux diverses façons de les approcher par des fractions faites de nombres entiers, c’est-à-dire par des nombres rationnels.
On se donne un irrationnel $\alpha$ (par exemple $\pi$ ou $\sqrt{2}$), et on se demande quelles sont les fractions irréductibles $\displaystyle \frac{a}{q} \in \mathbb{Q}$ qui permettent d’approcher suffisamment près $\alpha$. Bien sûr on peut approcher $\alpha$ aussi près que l'on veut avec une infinité de nombres rationnels, donc la question fait vraiment sens lorsque l'on souhaite que l'erreur commise soit plus petite qu'une fonction qui dépend du dénominateur employé.
On sait par exemple que la fraction continue de $\pi$ peut être utilisée pour générer des approximations rationnelles successives. On écrit
$$\displaystyle \pi \approx 3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+0,003\;417}}}}}}\approx 3+{\cfrac {1}{7+{\cfrac {1}{15+{\cfrac {1}{1+{\cfrac {1}{292+0,6}}}}}}}}, \mathrm{ etc.}$$
On a grâce à cette méthode les approximations bien pratiques dans certaines utilisations : $\frac{3}{1}$, $\frac{22}{7}$, $\frac{333}{106}$, $\frac{355}{113}$, $\frac{103993}{33102}$, $\frac{104348}{33215}$, $\frac{208341}{66317}$, $\frac{312689}{99532}$, $\frac{833719}{265381}$, $\frac{1146408}{364913}$, $\frac{4272943}{1360120}$, $\frac{5419351}{1725033}$, etc.
Dans le cas général, et pour un irrationnel $\alpha$ donné, le théorème d’approximation de Dirichlet1 permet déjà de dire qu’il y a une infinité de fractions irréductibles qui vérifient $\left| \alpha - \displaystyle \frac{a}{q}\right| \lt \displaystyle \frac{1}{q^2}$.
La conjecture de Duffin-Schaeffer, devenue le théorème de Koukoulopoulos-Maynard généralise et précise ce résultat.
Le théorème s’énonce ainsi (voir 2) :
Théorème
Soit $ \psi:\mathbb {N} \rightarrow \mathbb {R} ^{+}$ une fonction quelconque des entiers naturels vers les réels positifs ou nuls. Soit $\mathcal{K}$ l’ensemble de tous les nombres $\alpha\in [0, 1]$ pour lesquels on peut trouver une infinité de fractions irréductibles $\displaystyle \frac{a}{q} \in \mathbb{Q}$ qui vérifient $\displaystyle \left| \alpha - \frac{a}{q}\right| \lt \frac{\psi (q)}{q}$.
Alors $\mathcal{K}$ est de mesure de Lebesgue $\lambda (\mathcal{K})=1$ si et seulement si $$\displaystyle \sum _{q=1}^{\infty }\psi(q){\frac {\varphi (q)}{q}}=\infty ,$$
où $\varphi$ est l’indicatrice d’Euler1.
Si le théorème d’approximation de Dirichlet permet d’affirmer qu’il y a une infinité de fractions disponibles lorsque $\displaystyle \psi(q)=\frac{1}{q}$, il s’avère que même une petite variation de $\psi$ peut rendre impossible l’approximation de certains nombres irrationnels $\alpha$ avec la nouvelle contrainte d'erreur.
En juillet 2019, les mathématiciens Dimitris Koukoulopoulos de l’université de Montréal (Canada) et James Maynard du Mathematical Institute à l’université d’Oxford (Royaume-Uni), avait annoncé qu’ils avaient réussi à établir le résultat énoncé sous forme de conjecture par Duffin et Schaeffer dès 1940. Le résultat a été depuis publié dans la revue Annals of Mathematics en juillet 2020.
Le théorème obtenu montre essentiellement que la divergence de la série implique l’existence de l’approximation rationnelle.
L’implication inverse est une conséquence du lemme de Borel-Cantelli (celui dans le sens le plus connu).
En effet, soit $E_1, E_2, \dots $ une suite d’événements dans un espace probabilisé $(X,\mathcal{A},\lambda)$. Le lemme de Borel-Cantelli1 affirme que si $\displaystyle \sum_{n\geq 0} \lambda(E_n) \lt +\infty$ alors $\lambda(\limsup_{n} E_n)=0$.
Dès 1924, Aleksandr Yakovlevich Khinchin, connu pour ses travaux en théorie des probabilités, avait obtenu un résultat dans la même veine que la conjecture proposée quelques vingt ans plus tard par Duffin et Schaeffer.
Dans leur article Koukoulopoulos et Maynard rappellent l’approche de Khinchin.
On suppose ici que la suite $\left( q\psi(q)\right)_{q\geq 1}$ décroit (une hypothèse forte) et que les fractions rationnelles sont telles que $0\leq a \leq q$. Khinchin a montré que si $\displaystyle \sum_{q\geq 1} \psi(q) \lt +\infty$, alors $\lambda(\mathcal K)=0$ ; et si la série diverge, alors $\lambda(\mathcal K)=1$.
Intuitivement comme le suggèrent Koukoulopoulos et Maynard, on peut considérer les ensembles
$$\mathcal{K}_q=[0,1]\cap \bigcup_{a=0 }^q \left[ \frac{a-\psi(q)}{q},\frac{a+\psi(q)}{q} \right]$$
de façon à avoir $\displaystyle \mathcal{K}= \limsup_{q\rightarrow\infty}\mathcal{K}_q$.
La première implication du résultat de Khinchin s’obtient en appliquant le lemme de Borel-Cantelli avec la mesure de Lebesgue sur $[0,1]$.
L’autre partie du théorème de Khinchin dévoile la réelle difficulté de nombreux résultats partiels établis jusqu’à celui de Koukoulopoulos et Maynard.
En effet, il existe bien un lemme un peu moins connu de Borel-Cantelli2 qui s’applique dans le cas des espaces de mesure finie et sous hypothèse d’indépendance : $\lambda(X)\lambda(E_j\cap E_k)=\lambda(E_j)\lambda(E_k)$ pour toutes les paires d'événements. Dans ce cas, si la série $\displaystyle \sum_{j}\lambda(E_j)$ diverge, on a bien que $\lambda$-presque tous les éléments de $X$ appartiennent à une infinité de $E_j$.
La difficulté dans le résultat de Khinchin, c’est que les $\mathcal{K}_n$ ne sont pas indépendants. On la contourne en montrant qu’il y a cependant « assez d’indépendance approchée » pour assurer que $\mathcal K$ est de mesure $1$.
C’est en tentant de comprendre comment se débarrasser de la condition forte qui impose que la suite $\left( q\psi (q)\right)_{q\geq 1}$ décroit que Duffin et Schaeffer ont pensé qu’il fallait se concentrer sur des fractions $\displaystyle \frac{a}{q}$ réduites et considérer les ensembles
$$\mathcal{A}_q=[0,1]\cap \bigcup_{\begin{array}{cc} 1\leq a\leq q\\ \mathrm{PGCD}(a,q)=1\end{array} } \left[ \frac{a-\psi(q)}{q},\frac{a+\psi(q)}{q} \right]$$
de façon à avoir $\displaystyle \mathcal{K}= \limsup_{q\rightarrow\infty}\mathcal{K}_q$.
Comme dans le cas du résultat de Khinchin, Duffin et Schaeffer ont alors conjecturé que
$$\sum_{q=1}^\infty \frac{\varphi(q)\psi(q)}{q}=\infty \Rightarrow \lambda(\mathcal{A})=1.$$
C’est ce premier résultat que le travail de Koukoulopoulos et Maynard établit. Le lecteur intéressé par le contexte général dans lequel s'inscrivent ces questions pourra consulter le livre Metric number theory de Glyn Harman 3.
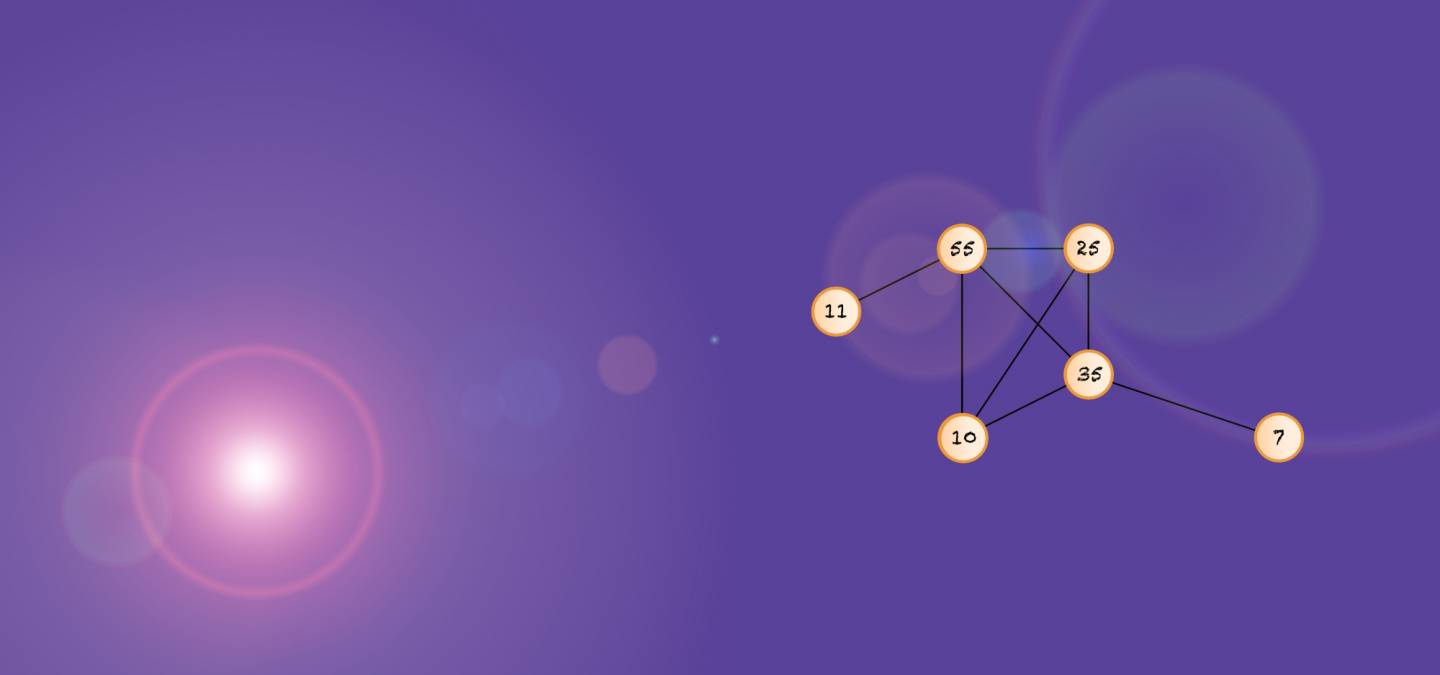
L’article de Koukoulopoulos et Maynard fait environ 50 pages que le lecteur motivé pourra lire. Il comporte une introduction historique du problème qui permet de saisir les points clés du travail effectué. Nous nous contentons ici de donner une idée essentielle de la preuve qui consiste à utiliser des graphes, appelés « graphes PGCD » ou « GCD graphs » en anglais, dont on mesure la complexité qui sera à son tour reliée à la possibilité de résoudre le problème.
Le graphe aide à visualiser les relations entre les différents dénominateurs : on relie deux dénominateurs par une ligne lorsqu'ils partagent un grand facteur
Ces graphes permettent de comprendre les liens entre des nombres entiers en signalant par un arc le fait qu’ils possèdent des diviseurs premiers communs. Une stratégie consiste à augmenter petit-à-petit la structure du graphe en passant d’un graphe $G_n$ à un graphe $G_{n+1}$ plus complexe, tout en conservant le fait que certaines informations importantes de $G_n$ restent contrôlées par $G_{n+1}$.
Un graphe-PGCD est la donnée d’un sextuplé $(\mu, \mathcal{V},\mathcal{W},\mathcal{E}, \mathcal{P},f,g)$ tel que :
a) $\mu$ est une mesure sur $\mathbb N$ telle que $\mu(n) \lt \infty$ pour tout $n\in \mathbb{N}$. On l’étend à $\mathbb{N}^2$ par la formule $\displaystyle \mu(\mathcal{N})=\sum_{(n_1,n_2)\in\mathcal{N}}\mu(n_1)\mu(n_2)$.
b) $\mathcal{N}$ et $\mathcal{W}$ sont deux ensembles d’entiers strictement positifs (les sommets du graphe, « Vertices » en anglais).
c) $\mathcal{E}\subset \mathcal{N}\times \mathcal{W}$ : donc $\mathcal{E}$ constitue l'ensemble des arêtes (« Edges » en anglais) d’un graphe biparti.
d) $\mathcal{P}$ est un ensemble de nombres premiers.
e) $f$ et $g$ sont deux fonctions de $\mathcal{P}$ dans $\mathbb N$ telles que pour tout $p\in\mathcal{P}$, on a :
i. $p^{f(p)}|v$ pour tout $v\in\mathcal{V}$ et $p^{g(p)}|v$ pour tout $v\in\mathcal{W}$ ;
ii. Si $(v,w)\in \mathcal{E}$ alors $p^{\min \{f(p), g(p)\}}$ est la plus grande puissance de $p$ qui divise $\mathrm{PGCD}(v,w)$ ;
iii. Si $f(p)\not = g(p) $, alors $p^{f(p)}$ est la plus grande puissance de $p$ qui divise $v$ pour tout $v\in\mathcal{V}$, et $p^{g(p)}$ est la plus grande puissance de $p$ qui divise $w$ pour tout $w\in\mathcal{V}$.
La mesure associée au graphe permet de mesurer l’ensemble $\mathcal{E}$ et donc d'évaluer la richesse du graphe.
La méthode utilisant des graphes est une véritable nouveauté dans le domaine qui a permis de rendre compte des relations complexes entre les entiers et les diviseurs qu'ils partagent.
Sur le site de l’université de Montréal, Koukoulopoulos précise les choses :
Prenons les dénominateurs 10 et 15. Ils ont un grand facteur commun : le nombre 5. Cela crée beaucoup d’approximations doubles, soit des nombres qui peuvent être approximés avec des fractions à la fois sur 10 et sur 15, comme 3/10 et 4/15, qui sont très près. Dans le graphe, les dénominateurs 10 et 15 seront reliés par une ligne. Par contre, 7, qui n’a pas de facteur commun, ne sera relié ni à l’un ni à l’autre.
Lorsqu’il y a trop de connexions dans le graphe, cela signifie que le dénominateur a trop de facteurs communs et qu’il rendra l’approximation de plusieurs nombres difficile. Pourquoi? Parce qu’on se retrouvera alors avec un petit bassin de nombres approximés par trop de fractions, tandis que la plupart des nombres n’auront aucune approximation. Donc, au final, il y aura trop de restrictions pour réaliser l’approximation de la majorité des nombres.
Il y aura probablement une suite et des conséquence inattendues à ce résultat qui s'énonce facilement mais qui a nécessité des techniques sophistiquées pour être démontré. Dans tous les cas, cet exemple illustre une nouvelle fois que des outils particuliers, ici la notion de graphe, ressurgissent à des endroits inattendus en mathématiques, et permettent d'éclairer de façon extrêmement puissante des situations qui semblaient ne pas avoir de points communs. C'est là un des aspects mystérieux des mathématiques que ce résultat récent et profond vient nous rappeler.