Nous allons voir que l'on dispose en fait de tous les renseignements nécessaires pour décrire la situation, à permutation près entre les couples (et à l'intérieur de chaque couple). Tout d'abord, le maître de maison à interrogé exactement $2n+1$ personnes ($n$ couples, plus sa femme), qui lui ont tous donné une réponse différente. Or une personne donnée ne peut serrer au maximum que $2n$ mains (celle des personnes qui ne sont pas son conjoint...). Les $2n+1$ réponses sont donc les entiers de $0$ à $2n.$

On représente les $2n+2$ personnes comme les sommets d'un graphe dont les arrêtes sont les poignées demain échangées. Une des personnes, que nous appellerons A, a serré exactement $2n,$ soit toutes celles des autres couples. La personne qui n'a serré aucune main est alors nécessairement son conjoint : toute autre personne a serré la main de A. Par élimination, le conjoint de A est la seule personne possible qui n'en a serré aucune.

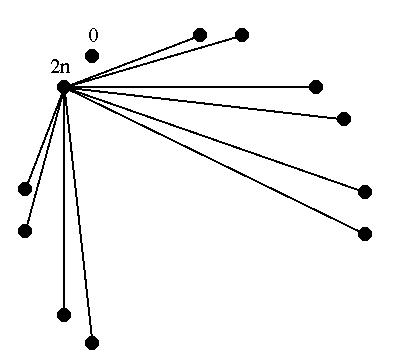
On peut alors conclure presque immédiatement : parmis les $2n$ personnes restantes, toutes ont déjà serré exactement une main. La personne qui a serré $2n-1$ mains a donc serré toutes les mains possibles en dehors de la personne qui en a serré zéro. Par le même raisonnement, c'est son conjoint qui en a serré une seule, toutes les autres personnes ayant serré au moins deux mains.

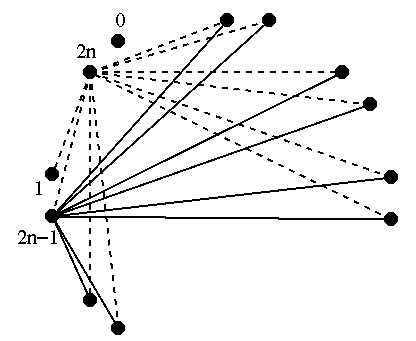
De proche en proche, on a ainsi la propriété suivante : le conjoint de la personne ayant serré $2n-i$ mains en a serré exactement $i$ (où, si l'on préfère, le total des mains serrées par un couple fait exactement $2n$). De proche en proche, on va ainsi épuiser tous les entiers de $0$ à $2n,$ jusqu'à arriver au dernier couple, dont les deux conjoints ont donc serré $n$ mains chacun.

Comme seulement une personne a déclaré avoir serré n mains, c'est que le maître de maison a lui-même serré $n$ mains, tout comme, donc, sa femme.

Le maître de maison, tout comme sa femme, a serré exactement $n$ mains.

N.B. Pour un peu plus de rigueur, on pourrait montrer notre résultat par récurrence sur $n.$ Supposons le résultat établi pour $n$ couples. Alors, lorsque l'on a $n+1$ couples invités, on se ramène à la situation précédente en éliminant le couple formé des personnes ayant serré respectivement $2n+2$ et $0$ mains, tous en enlevant une poignée de main à chacun des autres convives (celle échangée avec la personne en ayant serré $2n+2$).

En utilisant notre hypothèse de récurrence, le maître de maison a donc échangé $n$ poignées de main avec les personnes restantes, plus une avec la personne en ayant serré $2n+2,$ soit $n+1$ au total, ce qui achève la récurrence.