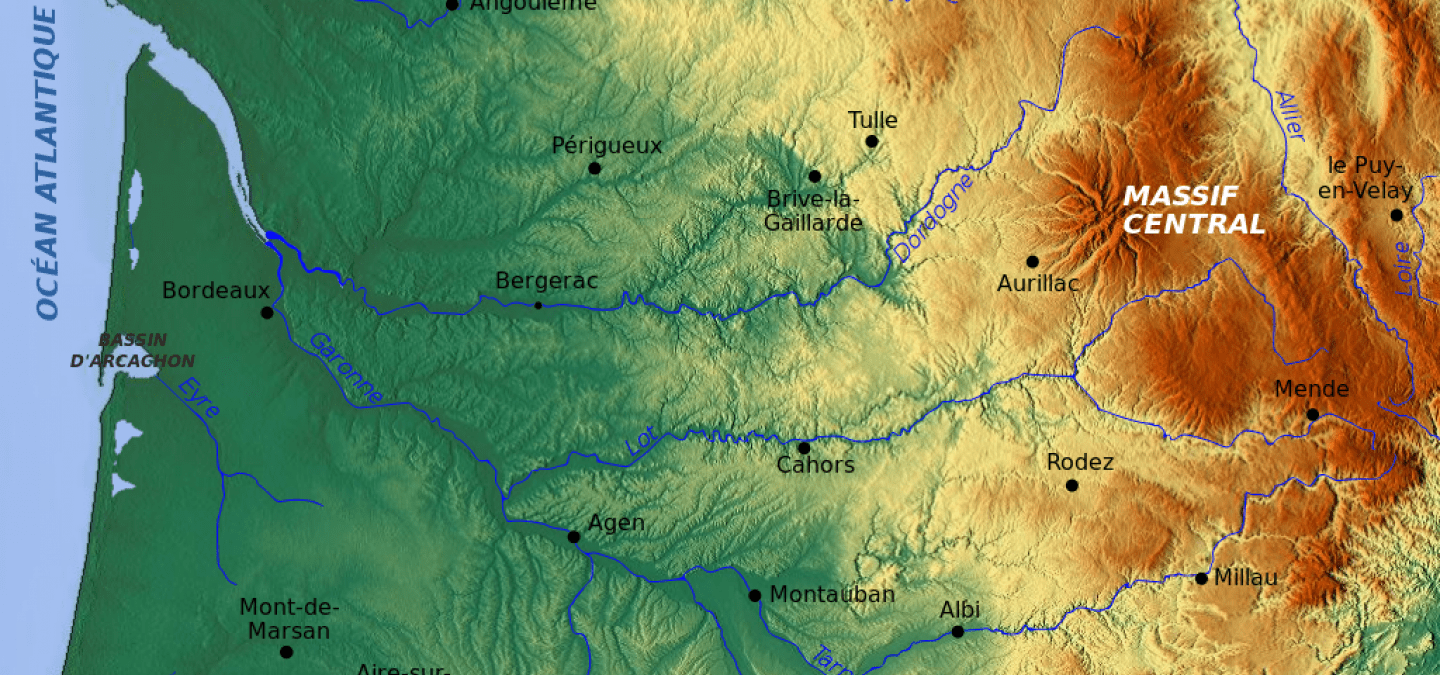
Nous passons en revue les mathématiciens, plus ou moins connus, de la période 16ème au 20ème siècle, et qui sont nés dans l’un des départements du « Grand Sud-Ouest » de la France (c’est-à-dire, en gros, les nouvelles régions administratives dénommées Occitanie et Nouvelle-Aquitaine). La présentation est faite sous forme de « vignettes historiques », sans difficultés mathématiques1.
Introduction
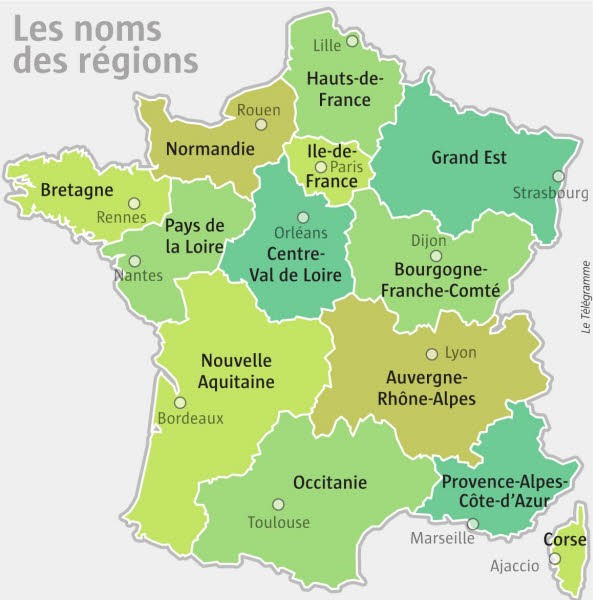
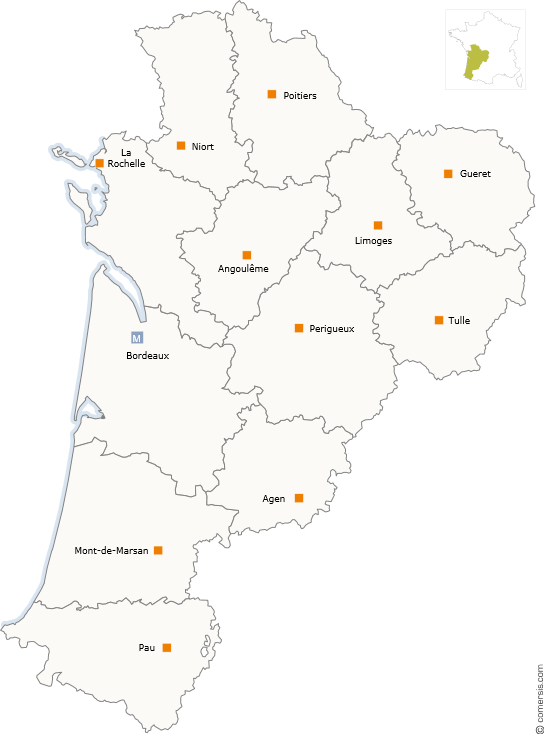
Mathématiciens originaires du « Grand Sud-Ouest » est un titre vague, qui demande d’entrée qu’on en précise l’objectif visé. D’abord, le contour géographique : il s’agira, en gros, de la partie de la France constituée des deux (nouvelles) régions administratives dénommées Occitanie et Nouvelle-Aquitaine ; nous nous en écarterons un peu vers le Nord de l’Occitanie, une seule fois (vers Aurillac). Ensuite, le vocable « mathématiciens » ; il recouvre des notions différentes suivant les siècles (en effet, à certaines époques, un scientifique pouvait être à la fois mathématicien, physicien, mécanicien, astronome, …), la forme moderne du métier de « mathématicien » étant plus précise et donc plus étroite. Jusqu’à la Révolution au moins, le vocable de géomètre était utilisé pour ce que nous appelons mathématicien aujourd’hui. Ce n’est qu’avec le développement des universités allemandes au 19ème siècle qu’apparaissent les mathématiciens professionnels.
Nous retiendrons dans notre étude les critères suivants :
-
Noms qu’un étudiant de mathématiques (dans son acception la plus large) peut rencontrer lors de ses études, ou bien qu’un intéressé par l’histoire des mathématiques et des mathématiciens peut croiser dans ses recherches.
-
Le lieu de naissance, plutôt que celui de son activité professionnelle, se trouve dans l’une des deux régions citées au-dessus. Nous avons utilisé pour ce repérage géographique des sites internet consacrés aux mathématiciens, en particulier celui de l’université Saint Andrews en Ecosse [1], ainsi que des ouvrages de biographies comme [2].
-
Le nom est encore vivace dans le village de naissance, sous des formes diverses, par exemple : appellation d’une rue, d’un établissement public, évocation sur le site web du village dans la rubrique « hommes et femmes illustres nés dans le village ».
A deux exceptions près (deux lauréats de la médaille Fields, un dans chacune des deux régions considérées), les personnes concernées sont décédées, parfois récemment.
Notre regard vers le passé ne remontera pas au-delà du 16ème siècle. Si quelqu’un est intéressé par une période plus ancienne, nous lui recommandons la lecture de l’excellent ouvrage [3], plus particulièrement du long texte de Jean Cassinet qui y figure.
Ici, nous commencerons notre voyage par les deux couloirs de passage vers l’Espagne : le passage méditerranéen par les Pyrénées-Orientales et le passage atlantique par les Pyrénées-Atlantiques (département dénommé Basses-Pyrénées jusqu’en 1969). Ensuite nous remonterons progressivement vers le Nord : départements de l’Hérault, du Gard, d’un côté ; départements des Landes, de la Gironde, de la Charente-Maritime, etc. jusqu’à la Creuse de l’autre. Nous terminerons par la partie la plus « centrale » du « Grand Sud-Ouest » : outre la Dordogne, les Hautes-Pyrénées, le Gers, le Tarn-et-Garonne et le Lot, des départements riches en mathématiciens comme l’Aveyron et la Haute-Garonne ; enfin, des mathématiciens ou mathématiques moins connus, comme ceux ayant des racines dans le département de l’Aude. Il est vrai que le cas de la Haute-Garonne (avec Toulouse) est un peu à part, il ne sera qu’effleuré car il est plus connu et, de toute façon, mériterait une étude à part à lui tout seul.
Notre évocation, qui est essentiellement historique, se terminera néanmoins par un joli résultat de mathématiques ; il est peu connu, facilement compréhensible (c’est de la géométrie dans l’espace, « en 3D » comme disent les ingénieurs) et dû à un Audois.
Le couloir méditerranéen
Pyrénées Orientales
Jean-Pierre Serre
A tout seigneur tout honneur… Dans ce département dominé par la famille des Arago (dont certains étaient un peu mathématiciens, au sens de leur époque)1, nous inaugurons notre voyage avec le village de Bages (à une quinzaine de kilomètres au Sud-Est de Perpignan). C’est là que naquit Jean-Pierre Serre (1925-). Grand spécialiste de ce domaine des mathématiques répertorié sous le nom de Géométrie algébrique, J.-P. Serre fut lauréat de la Médaille Fields en 1954 et le premier lauréat du Prix Abel en 20032. Le village de Bages le revendique (sur son site web) comme l’un des « hommes illustres nés dans le village ».
Hérault
Pierre Forcadel est un mathématicien du 16ème siècle, né à Béziers, frère du poète Etienne Forcadel. En 1560, Pierre Forcadel obtint une chaire de mathématiques au Collège de France, qu’il occupa jusqu’en 1574. Il fut poursuivi pour calvinisme pendant les guerres de religion. Il meurt entre 1576 et 1577. P. Forcadel fut précisément « Lecteur du Roy ès Mathématiques », un terme délicieux pour désigner la fonction de professeur de mathématiques au Collège Royal de France, fondé par François 1er. Il écrivit de nombreux livres de diffusion des mathématiques de son époque, des traductions françaises (comme la Géométrie d’Euclide en 1564), mais son plus grand mérite a été de réintroduire le symbole « + » pour marquer l’opération d’addition dans les calculs1. Comme quoi, ainsi qu’il m’arrive de le dire à des collègues ou étudiants en doctorat : « Rien ne sert de courir, il faut publier à point … ».
Joseph Boussinesq
Joseph Boussinesq (1842-1929) est un mathématicien et hydraulicien né à Saint-André-de-Sangonis (bourgade située à mi-chemin entre la Méditerranée et l’Aveyron). Il étudia à Montpellier et fut d’abord professeur de mathématiques aux collèges d’Agde, du Vigan et du Gap. Il fut professeur de Mécanique à la Faculté des Sciences de Lille (où son souvenir est resté vivace, un laboratoire de recherche universitaire y porte son nom aujourd’hui). Il occupa la chaire de Mécanique (Physique Mathématique) à la Faculté des Sciences de Paris en 1896, où il succéda à Henri Poincaré. Il fut également élu à l’Académie des Sciences. Son nom est connu en Mécanique des Fluides (avec « l’approximation ou hypothèse de Boussinesq » par exemple). Il figure dans la liste des « personnalités liées à la commune de Saint-André-de-Sangonis ».
Pierre-Ossian Bonnet
Le mathématicien Pierre-Ossian Bonnet (1819-1892) est né à Montpellier. Il étudia la géométrie différentielle des surfaces (une formule porte son nom, « la formule de Gauss-Bonnet »). C’est à Bonnet qu’on doit la notion de courbure géodésique. Il fut élu à l’Académie des Sciences.
Ne quittons pas Montpellier sans signaler Louis Castel. Fils d’une famille aux origines béarnaises, le mathématicien et physicien jésuite Louis Castel naît à Montpellier en 1688 et meurt à Paris en 1757. Il enseigna à Toulouse, Pamiers, Cahors, Paris… Les philosophes des Lumières (ainsi D. Diderot) mentionnent souvent son Optique des couleurs (1740), dans lequel il décrit un clavecin oculaire dont le principe réside dans l’analogie postulée entre les sons et couleurs ([11]). Castel s’opposa aux théories de Newton (sur des bases religieuses), ce qui eut pour effet de retarder l’acceptation des théories newtoniennes en France.
Thierry Aubin
Toujours dans l’Hérault, mais dans une période très récente, signalons Thierry Aubin (1942-2009), né à Béziers. Ce mathématicien, dont les contributions portent sur la géométrie différentielle et les équations aux dérivées partielles non linéaires, fut membre de l’Académie des Sciences.
Gard
Gaston Darboux
Gaston Darboux (1842-1917) est né à Nîmes. Cet éminent mathématicien, parmi les élèves duquel figurent E. Borel et E. Goursat (voir plus bas), fut élu à l’Académie des Sciences en 1884 et secrétaire perpétuel de cette même académie en 1890. Ses nombreux travaux concernent l’étude des surfaces, l’intégration, et les équations aux dérivées partielles. Un lycée professionnel et une rue portent son nom à Nîmes. La cour d’honneur du lycée A. Daudet de Nîmes accueille le buste de G. Darboux (qui fut inauguré en 1933).
Né dans le même département du Gard, nous avons Eugène Rouché (1832-1910). Rouché est né à Sommières (bourgade à une trentaine de kilomètres à l’Est de Nîmes). Il est connu pour le théorème de Rouché sur les zéros et les pôles des fonctions de la variable complexe, et un autre théorème, dit de Rouché-Fontené, relatif aux solutions d’un système d’équations linéaires. Il est amusant de noter que ce dernier théorème revêt différentes appellations suivant les pays : Rouché-Frobenius (en Espagne), Kronecker-Capelli (en Italie), ou même Rouché-Capelli.
Antoine Deparcieux
Allons plus au Nord, du côté d’Alès. Antoine Deparcieux, dit aussi de Parcieux (1703-1768), est né à Portes près d’Alès. Il s’intéressa aux applications sociales des mathématiques ; son ouvrage le plus célèbre fut « Essais sur les probabilités de la durée de la vie humaine ». Reçu à l’Académie des sciences en 1746. Comme la plupart des savants de son époque, il s’occupa aussi de plusieurs domaines de la Mécanique et de l’Hydraulique. Il figure, seul, sur la liste des personnalités liées à la commune de Portes.
Jacqueline (Lelong-)Ferrand
Dans une période plus récente, Jacqueline (Lelong-)Ferrand (1918-2014) est une mathématicienne née à Alès. En recherche mathématique, elle est connue comme une spécialiste de la représentation conforme, de la théorie du potentiel et des variétés riemanniennes. Après une thèse d’Etat en 1942 sous la direction d’A. Denjoy, elle commença sa carrière comme nommée chargée de cours à l’université de Bordeaux en 1943, pour la terminer Professeur à l’université de Paris à partir de 1956. Certains d’entre nous se souviennent que dans les années 1970, elle publia avec J.-M. Arnaudiès une série de livres d’enseignement couvrant les programmes des premiers cycles universitaires et des classes préparatoires scientifiques.
En 2017, la Société Mathématique de France crée un prix Jacqueline Ferrand pour récompenser une opération pédagogique innovante dans le domaine des mathématiques ; la première édition aura lieu en 2018.
Elle ne figure pas dans la liste des personnalités nées à Alès ou dans les environs, où pourtant elle aurait été en bonne compagnie avec Laurent Blanc (1965-) joueur puis entraîneur de football, et Julien Doré (1982-) artiste chanteur.
Nous quittons ce couloir méditerranéen pour ce celui, atlantique, à l’Ouest.
Le couloir atlantique
Pyrénées-Atlantiques
Au Pays basque, il n’y a que Pierre Hérigone (vers 1580-1643) et Renau d’Elissagaray (1652-1719) que j’ai trouvés comme (partiellement) mathématiciens.
Il y a quelques incertitudes sur la vie de P. Hérigone, à commencer par son lieu de naissance1. Il fut professeur à Paris, a appartenu au cercle de Mersenne, a participé aux débats dynamiques de son temps dans les Académies (avec E. Pascal et bien d’autres), et surtout a écrit un Cursus Mathematicus en 5 tomes et un supplément qui est resté fameux (publié entre 1634 et 1642). Dans le 6ème volume, il expose la méthode de recherche d’extremum de Fermat, l’une des techniques les plus avancées de l’Analyse de l’époque. Fermat y fait d’ailleurs allusion dans une lettre de 1662 : « […] ma méthode est imprimée […] dans le sixième tome du Cours Mathématique d’Hérigone et j’en ai assez dit pour être entendu. » (cf. [12, page 91]). Systématiquement répertorié dans la famille des mathématiciens de la première moitié du 17ème siècle, P. Hérigone est aussi vu comme l’un des inventeurs du codage chiffre-lettre. Dans ces Cours, il propose par exemple de coder (remplacer) les chiffres par des lettres, consonnes ou voyelles et syllabes. Grâce à ce codage, on peut transformer les nombres compliqués à mémoriser en mots ou pseudo-mots, en choisissant à son gré une consonne, une voyelle ou une syllabe. Selon les historiens des mathématiques, Hérigone peut être vu comme l’héritier de F. Viète (1540-1603), mais ses notations et procédures de démonstration sont très différentes.2
Renau d’Elissagaray, dit « le petit Renau », né en 1652 à Armendaritz (petit village de l’intérieur du Pays basque français), fut un grand constructeur naval, bâtisseur de fortifications et de ponts, au service de Louis XIV. Ses techniques empruntaient beaucoup aux connaissances cartésiennes de la géométrie des courbes et surfaces (voir [4, 5]). Il fut élu à l’Académie des Sciences en 1699 et en fut son vice-président en 1714. Une pastorale3 lui fut consacrée au Pays basque en août 2007, dans laquelle, de manière assez étonnante, sont évoqués « son goût, par-dessus tout, pour l’étude des mathématiques » et les noms de N. de Malebranche, Jean Bernoulli, Fontenelle, Newton. Son ouvrage « Traité de ma méchanique des liqueurs » (comprenez : des fluides), publié en 1712, utilise le calcul différentiel, alors encore à ses débuts ; les applications entrevues concernent les interactions air-voiles d’un navire, coque du navire-eau, etc. Une rue porte son nom à St Jean-de-Luz.
Dans le même département, jetons un coup d’œil du côté du Béarn. Ignace Gaston Pardiès (1636-1673) est un jésuite béarnais mathématicien qui naquit à Pau et étudia à Toulouse. Il fut longtemps en relation avec A. Laloubère (cf. infra). I. Pardiès adopta vite les principes de Descartes et fut en correspondance avec Newton. Auteur du traité de statique intitulé « La statique, ou la science des forces mouvantes » (1673). Il meurt jeune, à 37 ans, des suites d’une fièvre contractée en se portant à l’aide de prisonniers à Bicêtre. Une rue porte son nom à Pau.
Il est étonnant, pour moi, de voir comment, en ce siècle où les communications n’étaient pas aussi faciles et développées qu’aujourd’hui, les scientifiques arrivaient à échanger : Renau d’Elissagaray a lu le traité de Pardiès, correspond avec Christiaan Huyghens, Jean Bernoulli, etc.
Landes
Jean-Charles (de) Borda
Jean-Charles (de) Borda (1733-1799), né à Dax en 1733 est le nom qui ressort dans ce département si l’on s’en tient aux critères retenus pour notre étude. La carrière de ce grand ingénieur naval, physicien, mathématicien, de renommée mondiale, a été bien étudiée dans de nombreux ouvrages. Ses contributions concernent l’hydraulique et la résistance des fluides, ainsi que les sciences de la décision (le fameux « paradoxe de Borda-Condorcet » à propos des élections au scrutin). Borda fut membre (fort jeune) de l’Académie des Sciences, de l’Académie de Marine, du Bureau des Longitudes, etc. Le nom de Borda est très présent à Dax, avec un lycée général et technologique, une société savante très active, etc.
Pas loin de Dax, est associé à la ville d’Aire-sur-Adour le nom de François de Foix-Candale (1512-1594). Probablement né en Ariège, celui-ci fut évêque d’Aire-sur-Adour de 1570 à 1594 et Captal de Buch de 1572 à 1587 (Captal de Buch désigne le seigneur de la province sud du pays de Buch, qui regroupe aujourd’hui les communes d’Arcachon, la Teste-sur-Buch et Gujan-Mestras). C’est François de Foix-Candale qui fonda la première chaire de mathématiques de l’université de Bordeaux et la dota d’une pension annuelle. Son titulaire était recruté sur concours public au cours duquel il devait exposer et résoudre deux conjectures géométriques. Il n’y a pas trace de son nom aujourd’hui à Aire-sur-Adour.
Gironde
Benjamin Olinde Rodrigues (1794-1851) est né à Bordeaux. Ce mathématicien et économiste français a travaillé surtout en géométrie. Son nom est resté associé à deux résultats : la « formule de Rodrigues » en Analyse et une autre « formule de Rodrigues » en Géométrie.
Jean Jacques Moreau
Dans une période plus récente, Jean Jacques Moreau (1923-2014), né à Blaye, est un mécanicien et mathématicien reconnu. Ses travaux ont porté sur l’analyse convexe et l’analyse dite non-régulière (nonsmooth analysis en anglais), dont il est considéré comme un des pères fondateurs. Son cours au Collège de France (1967) sur les fonctions convexes, vues de manière moderne, est resté un grand classique. Il fut très longtemps Professeur à l’université de Montpellier, après l’avoir été à l’université de Poitiers. Par sa trajectoire (lieux de naissance, d’exercice, et de décès), il fait en quelque sorte le lien entre les deux régions Nouvelle-Aquitaine et Occitanie.
Depuis 2016, un amphithéâtre de l’université de Montpellier (situé sur le campus de St Priest) porte son nom. Par ailleurs, un Prix J. J. Moreau en Optimisation sera créé sous l’égide de la SMAI à partir de 2018-2019.
Charente-Maritime
Nous remontons dans ce couloir longeant l’Atlantique pour aller à Montguyon en Charente-Maritime (département dénommé Charente Inférieure jusqu’en 1941). C’est là que naquit André-Louis Cholesky (1875-1918). Peu d’étudiants en Analyse numérique savent que Cholesky n’est pas un obscur polonais mais bel et bien un ingénieur militaire français originaire de Montguyon à quelques kilomètres au Nord de Bordeaux. C’est dans le but d’applications à la géodésie que Cholesky étudie la résolution de systèmes d’équations linéaires et introduit la « factorisation » qui porte aujourd’hui son nom. Le « procédé du commandant Cholesky » fut publié de manière posthume en 1924 dans le Bulletin géodésique de Toulouse. Son nom est mentionné dans la liste des « personnalités liées à la commune » de Montguyon.
Huguette Delavault
Un livre entier lui a été consacré récemment (cf. au-dessus) : C. Bresinski et D. Tournès, A.-L. Cholesky : Mathematician, Topographer and Army Officer. Ed. Birkhäuser-Springer (2014).
Dans une période plus récente, notons Huguette Delavault (1924-2003), née à Andilly (près de La Rochelle). H. Delavault fut une Professeure des universités en mathématiques particulièrement engagée et mobilisée pour le développement et l’amélioration de la place des femmes en sciences et techniques ; elle fut notamment membre fondatrice de l’association Femmes & Sciences en 2000.
En 2017, son nom a été proposé pour une rue du campus de l’université de Toulouse à Rangueil (juste en face des bâtiments de l’Institut de Mathématiques).
Charente
Charles-Augustin Coulomb
Bien qu’il soit davantage connu comme physicien et mécanicien, on se doit de noter ici Charles-Augustin Coulomb (1736-1806), né à Angoulême. En Mécanique, domaine qu’étudient aussi certains mathématiciens appliqués, les lois dites de Coulomb expriment sous une forme simplifiée l’intensité des forces de frottement qui s’exercent entre deux solides. Le nom de Coulomb est encore bien visible à Angoulême, où un lycée porte son nom ainsi qu’une rue.
Haute-Vienne
Raymond Couty
Raymond Couty (1919-2005) est un mathématicien né à La Barre, commune de Veyrac, dont les travaux de recherche ont porté sur la géométrie différentielle. Il est surtout connu comme un des « pères fondateurs » de l’université de Limoges1. Il y a créé le département de mathématiques et l’a dirigé pendant plus de vingt ans. Les sexagénaires que nous sommes se souviennent qu’il fut l’auteur, avec J. Ezra de l’université de Poitiers, de deux livres de formation en Analyse de premier cycle universitaire (dans la Collection U, Ed. Armand Colin, 1967), plusieurs fois réédités. Un amphithéâtre porte son nom à l’université de Limoges.
Creuse
Jean Favard
Jean Favard (1902-1965), né à Peyrat-La-Nonière (près d’Aubusson), fut un Analyste reconnu (théorie de l’Approximation notamment), dont des collègues retraités de l’université de Grenoble se souviennent encore avec respect et gratitude1. En 1957, aux côtés de L. Schwartz, il participa au jury de la thèse in absentia de Maurice Audin. Très attaché à sa Creuse natale, son souvenir y est resté vivace : une place et un chemin de promenade portent son nom à Peyrat-La-Nonière ; de même que le lycée polyvalent de Guéret.
Depuis 2003, le Comité des amis de Jean Favard parraine les Olympiades de mathématiques de l’académie de Limoges (concours national, organisé dans chaque académie, et destiné aux élèves de 1ère de lycées).
Lucien Le Cam
Lucien Le Cam (1924-2000), né à Croze (canton de Felletin), est une des figures majeures de la modernisation de la Statistique. Il fit l’essentiel de sa carrière à l’université de Californie à Berkeley ; un de ses ouvrages de référence est « Asymptotic methods in statistical decision theory ». Le village de Croze a aujourd’hui 215 habitants environ, il en avait 750 lorsque Le Cam y est né. Le Cam figure, seul, dans la rubrique des « personnalités liées à la commune ». Depuis 2001, une « conférence Le Cam » est organisée par la Société Française de Statistique, visant à promouvoir de nouvelles méthodes statistiques ou approfondir certaines théories.
Nous abordons à présent la partie plus centrale du « Grand Sud-Ouest ».
La partie centrale du « Grand Sud-Ouest »
Hautes-Pyrénées
Pierre Jean-Paul Henri (ou Henry) (1848-1907). Natif de Montpezat-Bétracq (Pays de Vic-Bilh au Nord-Ouest de Tarbes1) , c’est à Toulouse que cet officier imagine la méthode qui le rendra célèbre, à savoir, un procédé de vérification graphique de la loi normale de Gauss (appelé encore de nos jours « test de normalité par la droite de Henry »). Une salle d’enseignement porte son nom à l’université Paul Sabatier de Toulouse.
Gers
Arnaud Denjoy
Arnaud Denjoy (1884-1974). Né à Auch, A. Denjoy étudia les ensembles analytiques, les nombres transfinis et la théorie des fonctions de variables réelles ; il découvrit en 1912 le concept de totalisation, intégration plus puissante que celle de Lebesgue ; il contribua également à l’étude des systèmes dynamiques.
Membre de l’Académie des Sciences en 1942. Plus étonnant est qu’entre les deux guerres il fut conseiller général du Gers pendant plus de quinze ans1. Sur le site de la ville d’Auch, son nom figure parmi ceux des « personnalités célèbres nées à Auch ». Un amphithéâtre d’enseignement porte son nom à l’université Paul Sabatier de Toulouse.
Tarn-et-Garonne
Pierre de Fermat, l’énigmatique
A Beaumont-de-Lomagne, comment ne pas évoquer Pierre Fermat ((1601 ?-1665)1 né dans cette bourgade ? Beaucoup de choses ayant été dites et écrites à son sujet, nous nous contentons de renvoyer au site internet qui lui est consacré (celui de la commune de Beaumont-de-Lomagne ou via l’association Fermat-Sciences).
Signalons néanmoins qu’un tout nouveau livre vient d’être publié à son sujet (cf. [12] et photo de couverture ci-dessous) ; fruit du travail d’une dizaine d‘auteurs d’horizons disciplinaires variés, il fait le point des connaissances et donne à voir de nombreux documents originaux.
Pierre de Fermat, l’énigmatique. Sous la direction de Marielle Mouranche. Toulouse, Université fédérale Toulouse Midi-Pyrénées. Editions midi-pyrénéennes (2017).
Mais il y aussi Théodore Despeyroux (1815-1883) qui est né à Beaumont-de-Lomagne. Docteur en sciences mathématiques, il fut chargé de chercher à Vienne (Autriche) des manuscrits inédits de Fermat ; il fut aussi suppléant dans un cours de calcul des probabilités de l’Université de Paris, puis professeur de mathématiques à Dijon. Il regagne Toulouse en 1868 comme professeur d’astronomie à la Faculté des Sciences et directeur de l’Observatoire municipal de Toulouse. Il a publié de nombreux mémoires dans le cadre de l’Académie des Sciences, Inscriptions et Belles-Lettres de Toulouse. A Beaumont-de-Lomagne, il fut également un généreux donateur et mécène, par exemple en offrant la statue de Fermat et sa bibliothèque de livres. Une rue ainsi que le collège portent son nom à Beaumont-de-Lomagne.
Dordogne
Jean-Frédéric Frenet
Jean-Frédéric Frenet (1816-1900). J.-F. Frenet était originaire de Périgueux. Sa thèse à Toulouse (1847) contenait explicitement une partie des formules concernant les courbes de l’espace, connues depuis comme les formules de Frenet-Serret ; Serret proposera la totalité de ces formules. Il fut professeur à Toulouse et à Lyon. Son nom figure dans la liste des « personnalités liées à Périgueux ». Un amphithéâtre d’enseignement de premier cycle porte le nom de Frenet à l’université Paul Sabatier de Toulouse.
Lot
Edouard Goursat
Edouard Goursat (1858-1936) est né à Lanzac, commune des Causses du Quercy dans le Lot. C’est un mathématicien dont le « Cours d’Analyse » fit longtemps école. Il consacra l’essentiel de ses recherches aux fonctions de la variable complexe, aux intégrales abéliennes, et à leurs applications à la résolution des équations différentielles. E. Goursat fut enseignant à l’université de Toulouse de 1881 à 1885, puis à Paris. Elu à l’Académie des Sciences en 1919. Son nom est mentionné dans la liste des « personnalités de la commune » du site web de la commune de Lanzac. Il y a aussi une rue Goursat à Limoges.
Corrèze
Cédric Villani
Ne quittons pas le nord du Lot sans une petite incursion en Corrèze (département qui, à présent, fait partie de la région Nouvelle-Aquitaine). C’est en effet à Brive que naît et accomplit une partie des études secondaires Cédric Villani (1973-), le mathématicien le plus médiatisé du moment. Les travaux de recherche de cet analyste et probabiliste ont permis une meilleure compréhension mathématique de plusieurs phénomènes physiques. Médaille Fields en août 2010 au congrès international des mathématiciens à Hyderabad (Inde), C. Villani fut aussi lauréat du Prix Fermat de recherche mathématique à Toulouse (édition de 2009). Sur le site web de la ville de Brive, son nom apparaît dans la liste « des personnalités natives de Brive », juste à côté de trois sportifs internationaux, l’un de football, les deux autres de rugby. Villani a été élu député à l’Assemblée Nationale en juin 2017.
Aveyron
Emile Borel
Avec l’Aveyron nous abordons un département riche en évocations de mathématiciens. A Saint-Affrique, nous avons Emile Borel et Pierre-Frédéric Sarrus. Nous avons consacré un long article aux mathématiciens du Rouergue (Borel, Sarrus, Deltheil) [6], et nous avons évoqué dans [7] Gaston Tarry, lequel est né à Villefranche-de-Rouergue. Nous ne nous n’y appesantissons donc pas. Quelques mots toutefois sur E. Borel et P. Sarrus.
Emile Borel (1871-1956). Les travaux de E. Borel, mathématicien né à Saint-Affrique concernent la théorie de la mesure, l’étude des fonctions de variables réelles et la sommation des séries, puis ils se tournent vers la théorie des Probabilités et la Physique mathématique. On lui doit aussi des écrits sur l’histoire des sciences, la philosophie, la psychologie, la pédagogie et l’économie politique.
Membre de l’Académie des Sciences en 1921. Député de l’Aveyron de 1924 à 1936, ministre de la Marine en 1925.
P.-F. Sarrus (1798-1861) étudia à Montpellier, il fut enseignant dans le secondaire à Pézenas et à Perpignan. Il devint ensuite professeur à la Faculté des Sciences de Strasbourg. Ses contributions concernèrent la Calcul des variations, la Mécanique (les dites « articulations de Sarrus » par exemple), mais les étudiants de première ou deuxième année universitaires le connaissent surtout par « la règle de Sarrus », un moyen mnémotechnique très particulier pour calculer les déterminants de matrices 3 par 3.
Complétons la visite du Rouergue en évoquant R. Deltheil.
Robert Deltheil (1890-1972). Né à Villefranche-de-Rouergue (Aveyron), R. Deltheil, fils de meunier, réussit de brillantes études en Mathématiques, marquées d’un premier coup d’arrêt par la Grande Guerre où il est blessé et décoré en 1915. Professeur à Toulouse depuis 1919, il succède à Paul Sabatier comme doyen de la Faculté des Sciences, puis devient recteur d’académie à Caen puis à Toulouse (1937). Arrêté alors qu’il était recteur, et déporté au camp de Neuengamme de juin 1944 à juin 1945, il refuse à son retour des postes prestigieux pour revenir enseigner à la Faculté des sciences de Toulouse, et ce jusqu’à sa retraite en 1961. Deltheil est connu comme un grand formateur ; il a exercé une influence certaine par ses nombreux ouvrages pédagogiques et sa forte personnalité. Son penchant profondément humaniste le conduisit aussi vers des activités universitaires d’intérêt général : très jeune doyen puis recteur.
Ne quittons pas le Nord de la région Occitanie, en s’en écartant un peu, sans évoquer Gerbert d’Aurillac. Gerbert d’Aurillac (circa 940-1003) est un aquitain d’origine1. Il étudia en Catalogne (Barcelone, Ripoll, Vich) et était secrétaire de Hugues Capet au moment où celui-ci fut couronné. Il est surtout connu comme étant le pape de l’an mil (en 999), le pape Sylvestre II. C’est assurément un des plus grands savants de son temps. Passionné par les mathématiques et l’astronomie, fut un novateur, le premier à avoir tenté d’introduire dans l’Occident chrétien la numération décimale de position, héritée des arabes.
Puisque nous sommes dans le département du Cantal, mentionnons P. Nicolas et M. Mourgues (cf. [11]). Pierre Nicolas (né à St Flour en 1663, décédé à Toulouse en 1718), jésuite mathématicien, acquit une renommée indiscutable dans les cercles scientifiques et académiques français, si l’on en croit les témoignages élogieux de plusieurs de ses contemporains. Michel Mourgues (né près de St Flour en 1642, décédé en 1713 à Toulouse) est un père jésuite qui fut professeur de mathématiques (et de rhétorique). Il fut titulaire d’une chaire royale à l’Université de Toulouse jusqu’en 1712. Ses livres, d’abord publiés à Toulouse, connurent un certain succès, ils furent vendus à Paris et Amsterdam.
Haute-Garonne
A côté de l’incontournable Pierre Fermat, évoqué plus haut lors de notre visite dans le Tarn-et-Garonne, mentionnons des activités intéressantes et de haut niveau des jésuites de la région toulousaine :
Antoine de Laloubère (1600-1664), né à Rieux-Volvestre près de Toulouse2. Ami de Fermat. Comme évoqué plus haut, A. Laloubère fut en relation avec le béarnais Ignace Pardiès, mais aussi avec l’anglais John Wallis. Ce fut l’enseignant de mathématiques toulousain le plus renommé de l’époque.
Nicolas Fizes (1648-1718), de Frontignan (Hérault). Il fut Professeur à l’université de Montpellier, où il enseigna les mathématiques et l’astronomie.
Emmanuel Maignan (1601-1676). Elève des jésuites, il entre ensuite dans l’ordre des minimes. Il enseigna les mathématiques à Toulouse, au couvent des Minimes de 1625 à 1636, puis à Rome, et de nouveau à Toulouse de 1650 à sa mort.
Dans une période plus récente, notons Gabriel Koenigs (1858-1931), mathématicien et mécanicien français né à Toulouse. Son nom est souvent confondu avec celui de S. Koenig (1712-1757), mathématicien allemand à qui l’on doit deux « théorèmes de Koenig » sur le moment et l’énergie cinétique. G. Koenigs fut Professeur à Paris, élu à l’Académie des Sciences dans la section Mécanique en 1918. Contemporain de G. Darboux (cf. supra), il a contribué dans le domaine de la Géométrie puis celui de la Mécanique analytique. A Toulouse, un boulevard porte son nom.
Tarn
Je n’ai pas trouvé trace de mathématicien né dans le département du Tarn. Toutefois, je me dois de signaler le fait suivant, peu connu, c’est l’implication politique de C. Dupin à Castres. Charles Dupin (1784-1873) est un géomètre, ingénieur naval et homme politique. Il est connu en mathématiques pour ses contributions en Géométrie différentielle (courbure des surfaces, ladite indicatrice de Dupin) ; les applications qu’il en avait concernaient la construction des vaisseaux (de guerre surtout). C. Dupin fut élu député pour le 2ème arrondissement du Tarn (à Castres) en novembre 1827. Il ne parvint pas à reconquérir son siège de député à Castres en 1830, mais il rentra à la Chambre comme député du 10ème arrondissement de Paris.
Aude
Nous terminons notre tour avec le département de l’Aude. C’est un peu par hasard il y a une quinzaine d’années que je suis tombé sur le nom de Jean-Paul Gua de Malves (1712-1786). Au début, je pensais qu’il s’agissait d’un portugais ou d’un espagnol, et je prononçais mal son nom. En fait, Jean-Paul Gua est né à Carcassonne. Sa famille fut ruinée par les spéculations du système de Law. Il décida de devenir ecclésiastique, car c’était une formation et une fonction rémunérées. Il fut prieur de Saint-Georges-de-Vigou. Il deviendra Professeur au Collège Royal. Il est connu comme le premier concepteur de l’Encyclopédie ; Denis Diderot lui succédera à la tête du projet. A sa mort, Condorcet en fera un éloge appuyé.
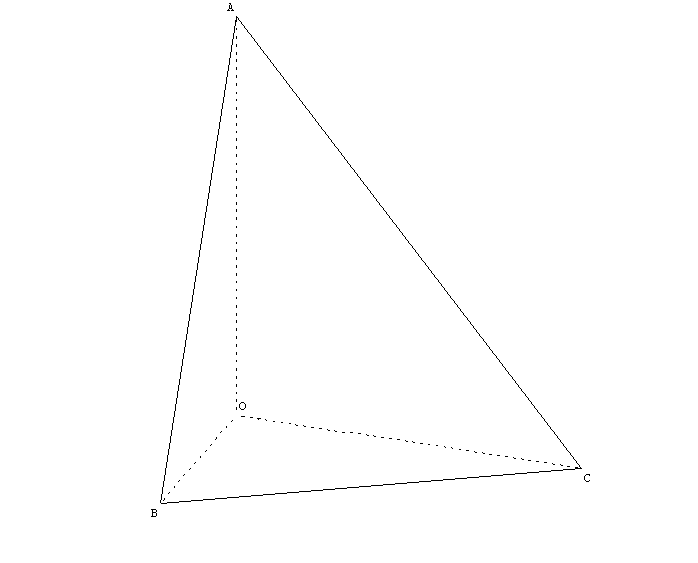
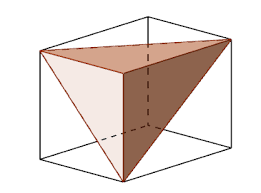
Je vais à présent présenter succinctement « le théorème de Gua » (1783), un résultat de géométrie en trois dimensions, qui est l’analogue du théorème de Pythagore dans le plan. Avec deux collègues, nous avons publié une note sur le sujet [8], ce qui nous a permis de toucher un lectorat important, comme en témoignent les nombreuses réactions que nous avons reçues depuis ([9, 10]). Le théorème en question dit ceci : Dans un tétraèdre trirectangle (avec trois faces qui sont des triangles rectangles, et une face hypoténuse qui est un triangle sans propriété), la surface (les mathématiciens diraient « l’aire ») du triangle hypoténuse se calcule à partir des surfaces des trois triangles rectangles ; de fait, le carré de la surface de la face hypoténuse est égal à la somme des carrés des surfaces des trois triangles rectangles.
Une fois qu’on connait le résultat, plusieurs démonstrations sont possibles (comme souvent en mathématiques), suivant ce que l’on sait (en utilisant la géométrie des triangles dans l’espace, en utilisant le produit vectoriel, en passant par les formules donnant le volume d’un polyèdre convexe). Nous l’avons signalé à des professeurs de Terminales de lycées, nous-même le proposions en exercice de manière régulière aux étudiants de deuxième année universitaire de la filière « sciences pour l’ingénieur ». R. Descartes était sans doute familier du résultat, mais il ne le publia jamais. Le théorème de Gua est redécouvert régulièrement, mais notre étude historique dans [8] nous confirme que c’est bien à Gua qu’on doit la démonstration et diffusion de ce beau résultat de géométrie en trois dimensions1.
Références :
1. MacTutor History of Mathematics Archive. Site internet en libre accès de l’Université de Saint-Andrews en Ecosse.
2. B. Hauchecorne et D. Suratteau, Des mathématiciens de A à Z. Editions Ellipses, 3ème édition (2008).
3. Huit siècles de mathématiques en Occitanie : des Arabes & de Gerbert d’Aurillac à Pierre de Fermat. Actes du colloque de Toulouse & de Beaumont-de-Lomagne (10-13 décembre 1992). Republié par les Editions PyréMonde (2008).
4. J.-J. Briost, L’ingénierie cartésienne de Renau d’Elissagaray. Documents pour l’histoire des techniques, n° 16, 169-186 (2008).
5. Bernard Renau d’Elissagaray, dit petit Renau : marin, ingénieur, mathématicien, et même fiscaliste. Conférence de R. Elissagaray de Jaurgain à la société Eusko Ikaskuntza (Bayonne) le 27 mars 2004.
6. J.-B. Hiriart-Urruty et H. Caussinus, Sarrus, Borel, Deltheil : Le Rouergue et ses mathématiciens. Gazette de la Société mathématique de France n° 104, 88-97 (2005).
7. J.-B. Hiriart-Urruty, Y a-t-il des mathématiques derrière les grilles de sudoku ? Quadrature n° 73, EDP Sciences, 43-48 (2009).
8 a,b. J.-P. Quadrat, J.B. Lasserre, and J.-B. Hiriart-Urruty, Pythagoras’ theorem for areas. American Math. Monthly, 549-551 (2001).
9. C. Mariconda, Courrier à l’Auteur en date du 3 juillet 2000.
10. J.-M. Lévy-Leblond, Courrier à l’Auteur en date du 22 septembre 2004.
11 a,b. M. Spiesser, Esquisses de biographies de P. Nicolas, I. G. Pardies, M. Mourgues, L.-B. Castel, etc. (travaux en cours).
12 a,b. Pierre de Fermat l’énigmatique. Ouvrage collectif publié sous la direction de Marielle Mouranche. Editions midi-pyrénéennes – Université fédérale Toulouse Midi-Pyrénées (2017).