En classes de Première et Terminale 12, le lycéen croisera parfois deux formules de l'espérance d'une variable aléatoire (discrète finie) $X$. Voyons cela quand \[X:\Omega = \{\omega_1,\omega_2,\dots,\omega_n\} \rightarrow X(\Omega) = \{x^1,x^2,\dots,x^p\} \subset \mathbb{R}\] où, pour différencier les éléments de l'univers $\Omega$ de ceux du support $X(\Omega)$, nous avons énuméré les uns par des indices $i$, les autres par des exposants $j$.

La première formule moyenne sans répétition les images $x^1$, $x^2$, ..., $x^p$ de $X$ en les pondérant de leurs probabilités d'être atteintes. Soit \[ \color{green}{\mathrm{E}[X]}= \sum_{j=1}^p x^j \mathbb{P}_X([X = x^j]) \tag{1}\label{eq1} \] où $\mathbb{P}_X([X = x^j])$, défini par $\mathbb{P}(\omega \in \Omega \,/\, X(\omega) = x^j)$, correspond à la probabilité image de $\mathbb{P}$ par $X$. L'expression \eqref{eq1}, « pilotée par l'output », adopte une logique de sommation  en tranches dans l'esprit de l'intégrale de Lebesgue3. C'est la définition de l'espérance dont partent en général les statisticiens 45. Pour intuitive qu'elle soit, elle en occulte une propriété considérable, la linéarité, illisible sinon au prix de quelques contorsions.

La deuxième formule « rétro transfère » le calcul de $\color{green}{\mathrm{E}[X]}$ à l'univers $\Omega$ des issues. La somme obtenue procède alors d'une réorganisation de \eqref{eq1} que permettent la commutativité et l'associativité de l'addition. Elle moyenne de fait  avec répétition les images de $X$ par les fréquences des événements élémentaires, adoptant une logique de sommation en piles (un peu « à la Riemann6 », pour filer l'analogie7  de l'intégration), pilotée par l'input : \[ \color{green}{\mathrm{E}[X]}= \sum_{i=1}^n X(\omega_i) \mathbb{P}(\omega_i) \tag{2}\label{eq2} \] Cette deuxième écriture, plus formelle, est celle des probabilistes 891011. Pour être tout à fait honnête, il s'agit de la « vraie » définition de l'espérance, dont tout découle ensuite. En particulier que pour deux variables aléatoires $X$ et $Y$, $\color{green}{\mathrm{E}[X+Y]} = \color{green}{\mathrm{E}[X]}+\color{green}{\mathrm{E}[Y]}$, et ce sans avoir eu à déterminer la loi de $X+Y$. Le mécanisme du transfert de \eqref{eq2} vers \eqref{eq1} peut être appréhendé sur des exemples génériques, en les accompagnant d'une illustration. 

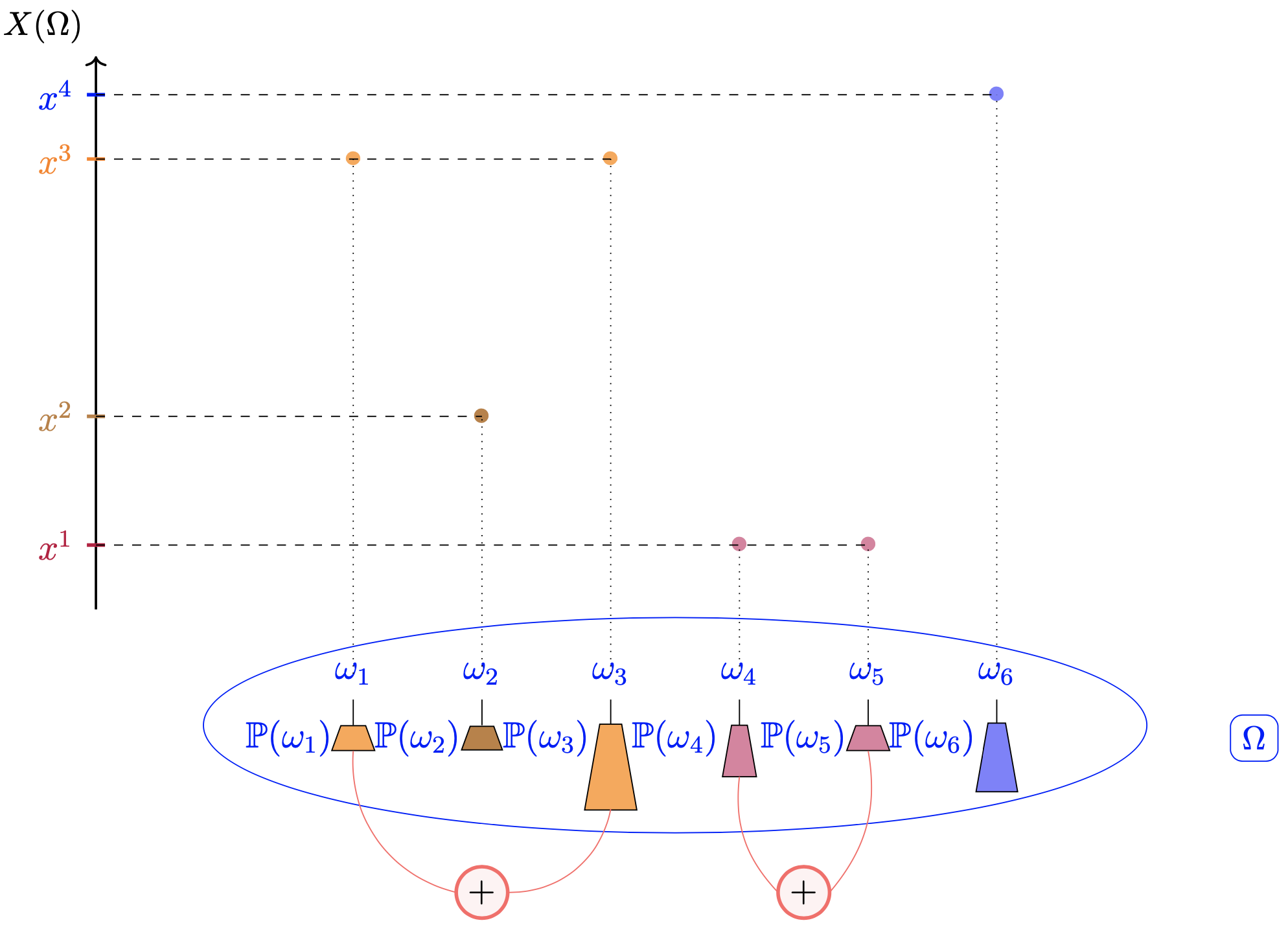
Proposons celle-ci, où les $n=6$ germes de probabilité sont figurées par de petits poids de valeur totale l'unité de masse et les $p=4$ images par de petites pastilles de couleurs assorties.

Partant de \eqref{eq2}, \begin{align*} \color{green}{\mathrm{E}[X]} = \color{orange}{x^3} \mathbb{P}(\omega_1)+\color{brown}{x^2} \mathbb{P}(\omega_2)&+\color{orange}{x^3} \mathbb{P}(\omega_3)\\ &+\color{purple}{x^1} \mathbb{P}(\omega_4)+\color{purple}{x^1} \mathbb{P}(\omega_5)+\color{blue}{x^4} \mathbb{P}(\omega_6) \end{align*} On débouche, en réassemblant, sur \begin{align*} \color{green}{\mathrm{E}[X]} = \color{purple}{x^1}\left[\mathbb{P}(\omega_4)+\mathbb{P}(\omega_5) \right] &+\color{brown}{x^2} \mathbb{P}(\omega_2)\\ &+ \color{orange}{x^3}\left[\mathbb{P}(\omega_1) + \mathbb{P}(\omega_3) \right]+\color{blue}{x^4} \mathbb{P}(\omega_6) \end{align*} Soit exactement \eqref{eq1} : \begin{align*} \color{green}{\mathrm{E}[X]} = \color{purple}{x^1 \mathbb{P}_X([X = x^1]})&+ \color{brown}{x^2 \mathbb{P}_X([X = x^2]})\\ &+\color{orange}{x^3 \mathbb{P}_X([X = x^3]})+\color{blue}{x^4 \mathbb{P}_X([X = x^4]}) \end{align*}