Que d'élégance dans les mathématiques 1. Songez donc : la dérivée d'une somme devient une somme de dérivées ; la dérivée d'une composée, un produit de dérivées ; la dérivée d'une réciproque, l'inverse d'une dérivée 2. À jouer sur les notations et la polysémie des lois, on obtient même des formules troublantes de concision, les deux dernières se résumant à : \[ (f \circ g)'(x) = f'{\scriptscriptstyle (g(x))} \,{\scriptstyle \bullet} \, g'(x) \] et \[ (f^{-1})'(x) = (f'{\scriptscriptstyle (f^{-1}(x))})^{-1} \] Les règles se font moins intuitives sur la dérivée d'un produit, d'un inverse, d'un quotient — toutes au programme de la spécialité de Première 3. Non, la dérivée d'un produit n'est pas un produit de dérivées ; pas plus une composée (au nom d'une pseudo dualité). Non, la dérivée d'un inverse n'est pas l'inverse d'une dérivée ; pas davantage une réciproque. Dès lors, on apprendra par cœur que \begin{equation} (f g)'(x) = f'(x)g(x)+f(x)g'(x) \label{eqPlus} \end{equation} et \begin{equation} \big(\tfrac{f}{g}\big)'(x)=\tfrac{f'(x)g(x)-f(x)g'(x)}{(g'(x))^2} \label{eqMoins} \end{equation} ainsi que leurs démonstrations. Par cœur, vraiment ? Quand un dessin rend compte de la relation \eqref{eqPlus} ? Qu'un autre éclaire la \eqref{eqMoins}, dont le curieux signe « $-$ » qui la distingue de \eqref{eqPlus} ?

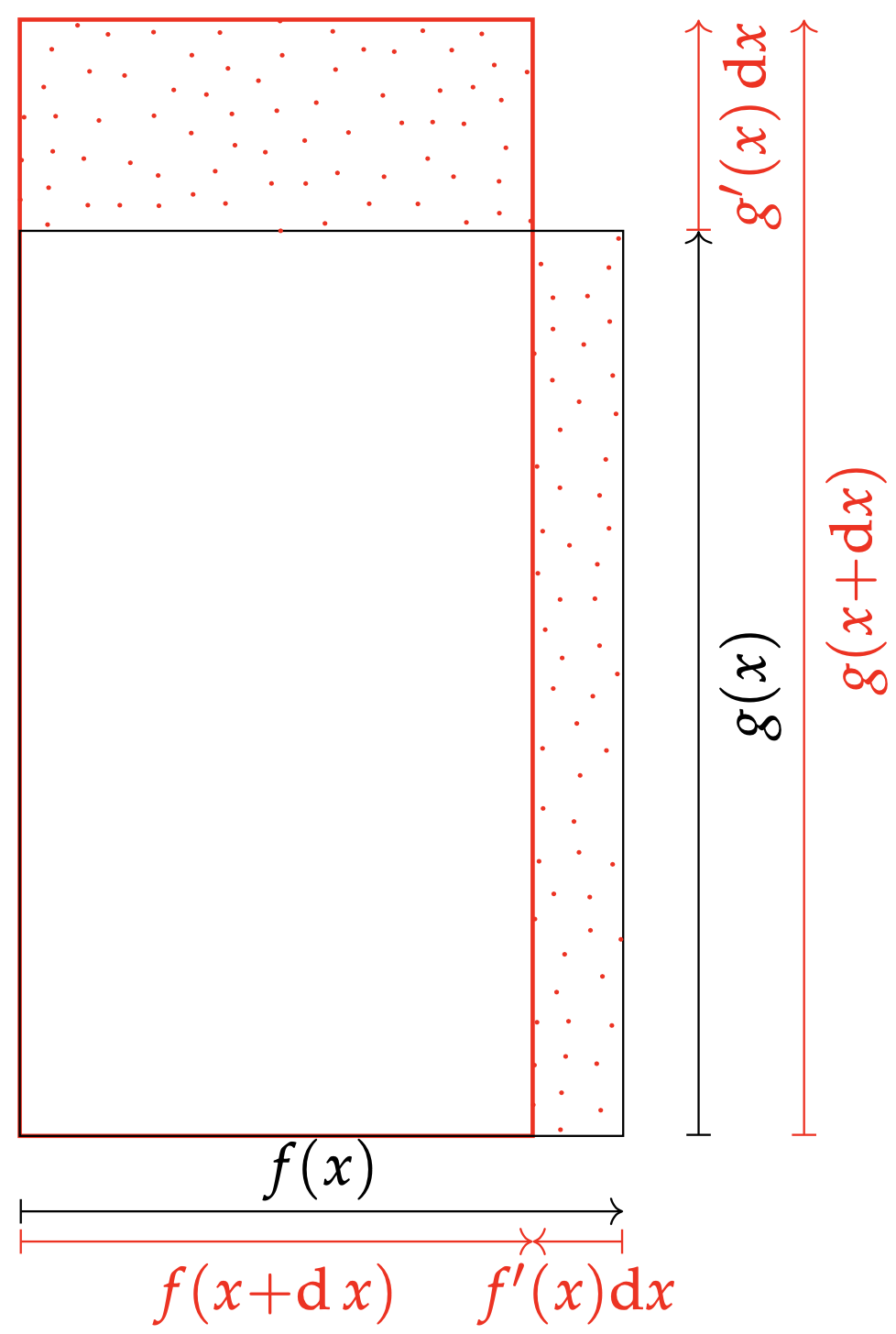
Pour établir de façon heuristique la formule \eqref{eqPlus}, on assimile $fg(x)=f(x)g(x)$ à l'aire algébrique d'un rectangle de côtés (signés) $f(x)$ et $g(x)$. Si bien que \begin{align*} \mathrm{d}(fg)(x) &= fg(x+\mathrm{d} x) - fg(x) \\ &= f(x+\mathrm{d} x)g(x+\mathrm{d} x) - f(x)g(x) \end{align*} apparaît comme une différence d'aires, ce qu'illustre le schéma ci-dessous.

Naturellement, les parties communes se compensent ; ne subsistent que deux franges, mouchetées sur le graphique. En atteste d'ailleurs le calcul, limité aux approximations affines \begin{align*} \mathrm{d}(fg)(x)&=f(x +\mathrm{d} x)(g(x) + g'(x)\mathrm{d} x)- (f(x+ \mathrm{d} x) - f'(x)\mathrm{d} x)g(x)\\ &=f(x +\mathrm{d} x)g'(x)\mathrm{d} x + f'(x)g(x)\mathrm{d} x \end{align*}

Dans le même esprit, en tronquant $f(x +\mathrm{d} x)g'(x)\mathrm{d} x = f(x)g'(x)\mathrm{d} x + f'(x)g'(x)\mathrm{d} x^2$ au premier ordre, il vient \[ \mathrm{d}(fg)(x) = \left(f(x)g'(x)+f'(x)g(x)\right)\mathrm{d} x \] qui justifie \eqref{eqPlus}.

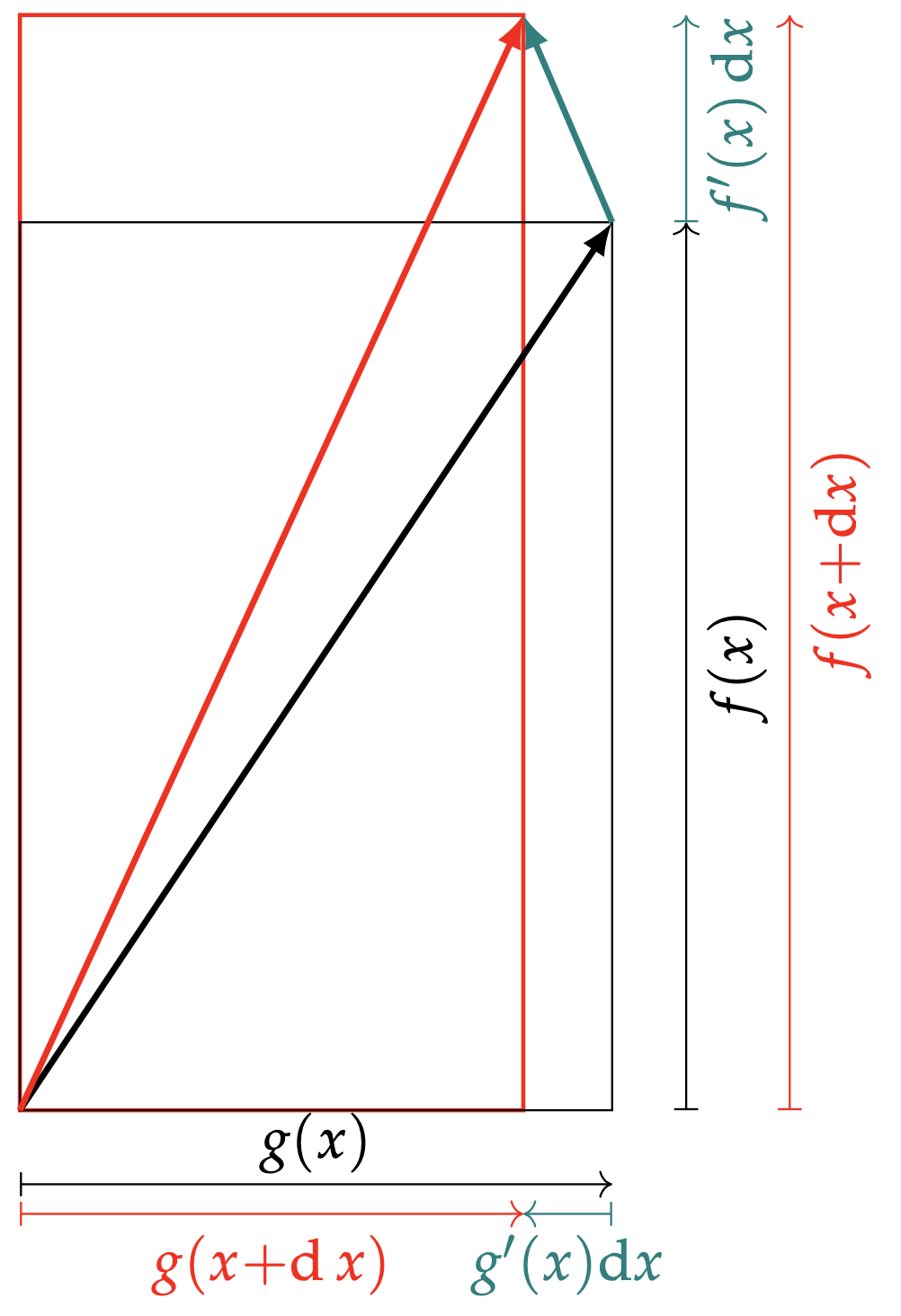
Pour expliquer de manière imagée la formule \eqref{eqMoins}, on interprète le quotient $\tfrac{f}{g}(x)=\tfrac{f(x)}{g(x)}$ comme la pente du vecteur $\left(g(x);f(x)\right)$. Si bien que \begin{align*} \mathrm{d}\big(\tfrac{f}{g}\big)(x)&=\tfrac{f}{g}(x+\mathrm{d} x)-\tfrac{f}{g}(x)\\ &=\tfrac{f(x+\mathrm{d} x)}{g(x +\mathrm{d} x) } - \tfrac{f(x)}{g(x)} \end{align*} compare deux pentes. Or la pente de $\left(g(x);f(x)\right)$ tend à croître (resp. décroître) quand le vecteur $\left(g(x);f(x)\right)$ tend à tourner dans le sens direct (resp. rétrograde). C'est-à-dire quand le vecteur déplacement infinitésimal $\mathrm{d}\left(g(x);f(x)\right)$, linéarisé en $\left(g'(x)\mathrm{d}x; f'(x)\mathrm{d}x\right)$, pousse $\left(g(x);f(x)\right)$ dans le sens trigonométrique. Une propriété que caractérise la positivité du déterminant \[ \begin{vmatrix} g(x) & g'(x)\mathrm{d}x \\ f(x) & f'(x)\mathrm{d}x \end{vmatrix} = \left(f'(x)g(x)-f(x)g'(x)\right)\mathrm{d}x. \] Aussi $\mathrm{d}\big(\tfrac{f}{g}\big)(x)$ et $\left(f'(x)g(x)-f(x)g'(x)\right)\mathrm{d}x$ sont-ils de même signe, et par conséquent $\tfrac{\mathrm{d}({f}/{g})}{\mathrm{d}x}(x)$ et $f'(x)g(x)-f(x)g'(x)$ aussi. Voilà qui corrobore \eqref{eqMoins} et que récapitule le croquis ci-après :