Coniques iconiques : ellipses, paraboles, hyperboles, mais que font ces figures de style en mathématiques ?
À la racine du mot
Comme ses cousines l’ellipse et l’hyperbole, la parabole est une figure de style avant d’être une conique. Le mot, issu du grec ancien, accole au préfixe ``para'', à savoir « contre/ à côté », qu’on retrouve dans « parasol », « paratonnerre » ou « parallèle », le suffixe ``ballein'', à savoir « jeter », qu’on retrouve dans « discobole », « balle » ou « balistique ». Il renvoie à l’exercice, érigé en art dans l’Antiquité, d’agencer des phrases et des images en regard les unes des autres pour en faire un récit, le cas échéant mythologique ou allégorique. Une évolution vers des formes aux sens plus populaires, mais non moins universels 1, donna les « paroles » et les « palabres ». Mais avant, c’est aussi à cette époque reculée qu’Aristée2 puis Apollonius3 conçurent d’intersecter le plan et le cône. En plaçant le premier en regard du second dans une position limite, parallèle à l'une des obliques de son profil, on obtient la parabole. Au-dessus (hyper est ce qui est au-delà) de cette ligne naissent les hyperboles, au-dessous (``elleipsis'' est ce qui est en moins) les ellipses, figure 1.

La figure s’anime grâce à deux appliquettes JavaScript / WebGL conçues pour l’occasion, disponibles sur le site CultureMath (voir ci-dessous).
Pour animer, visualiser ou encore modifier sur l'appliquette JavaScript / WebGL
- les trois sections d'un cône, le lien est ici,
- une section d'un cône, le lien est ici.
Pour avoir des exemples, voir la vidéo de la dernière section.
Il serait tentant de rechercher d’autres étymologies au mot « parabole ». Par exemple, que « poser/ jeter à côté », comme expliqué précédemment, évoque la courbe que décrit un objet « lancé par devant soi » ; ou bien rappelle la construction des coniques comme lieu géométrique obtenu via la « projection d’un point vers » un axe (en l'espèce, la directrice). Vraisemblablement, ce sont des raccourcis logiques et historiques. Dans le film et somptueux péplum, Agora 4, le cinéaste Alejandro Amenábar s'est plu à imaginer qu'Hypatie5, voilà mille-six-cents ans, était sur les traces de Kepler6 et de Newton7, et que la mort de son héroïne aurait interrompu pour longtemps l'élan de la recherche. Sans le développement de la géométrie analytique, le lien entre sections coniques d’une part, et définitions homofocale ou bifocale des coniques d’autre part, avait cependant toutes les raisons d’être flou. Il aura fallu des siècles de décantation pour que Dandelin8 trouve une passerelle directe 910, reposant sur des sphères. En revanche, sur une parabole, initialement définie par section conique donc, la dépendance quadratique entre abscisse et ordonnée — deux mots d'origine grecs en fait très antérieurs à Descartes11 — était, elle, connue bien avant notre ère 1213.
Aux racines de l’algèbre et de l'analyse
Dans ce qu’on considère être le premier traité d’algèbre, Al Khawarizmi14 détaille par le menu un procédé d’extraction des racines d’une équation du second degré particulière : $x^2+10x = 39$ 15. Interprétation géométrique à l'appui, sa méthode préfigure la mise sous forme canonique par complétion du carré, méthode étudiée aujourd'hui en classe de Première 16. Le calcul du discriminant et l'habituelle discussion qui porte sur son signe en découlent et sont en général traités au sein du même chapitre. À un moment ou à un autre du déroulé du programme cependant, il s'agira d'articuler ces considérations purement algébrique aux outils puissants de l'analyse auxquels l'élève commence à accéder à ce stade de sa scolarité. En voici quelques pistes. Soit donc la fonction trinôme $f$ définie sur $\mathbb{R}$ par $$ f(x) = ax^2+bx+c $$ avec $a \neq 0$.
Variations, extremum, allure selon le signe du coefficient de $x^2$. Ces capacités sont attendues des textes officiels. En résumé, l'application $f$ se dérive en $f'(x)=2ax+b$, expression affine dont la transition de signe se produit en $x_0 = -\frac{b}{2a}$. Selon que le coefficient dominant $a$ est positif ou négatif, la courbe de $f$ est « souriante » ou bien « contrariée » et présente en $x_0$ un minimum ou un maximum, figures 2 et 3. Approfondissons désormais.
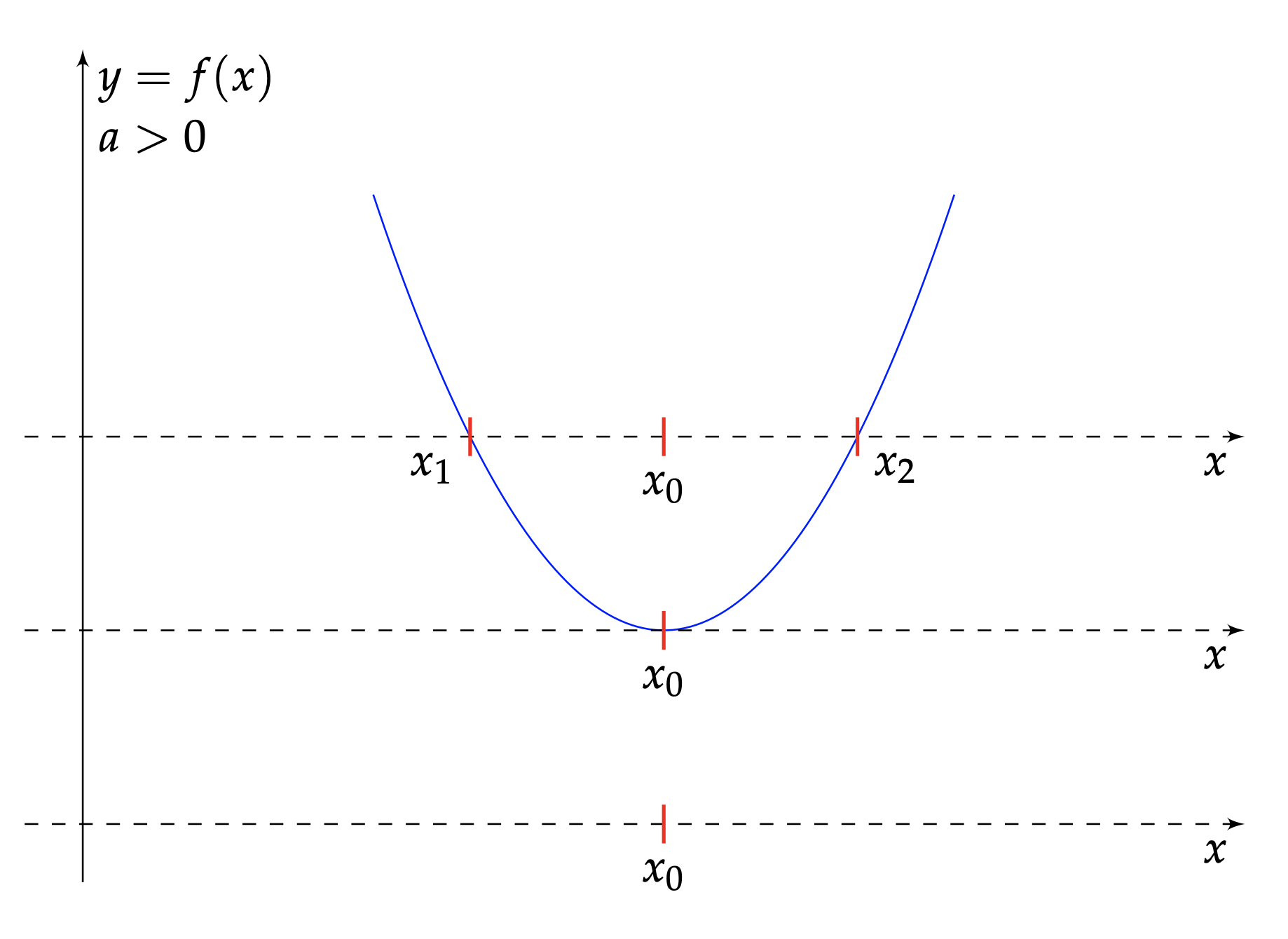
$a \gt 0$. Trois positions sont ici représentées, selon que la parabole traverse, tangente ou évite l’axe des abscisses (qui apparaît en pointillés).
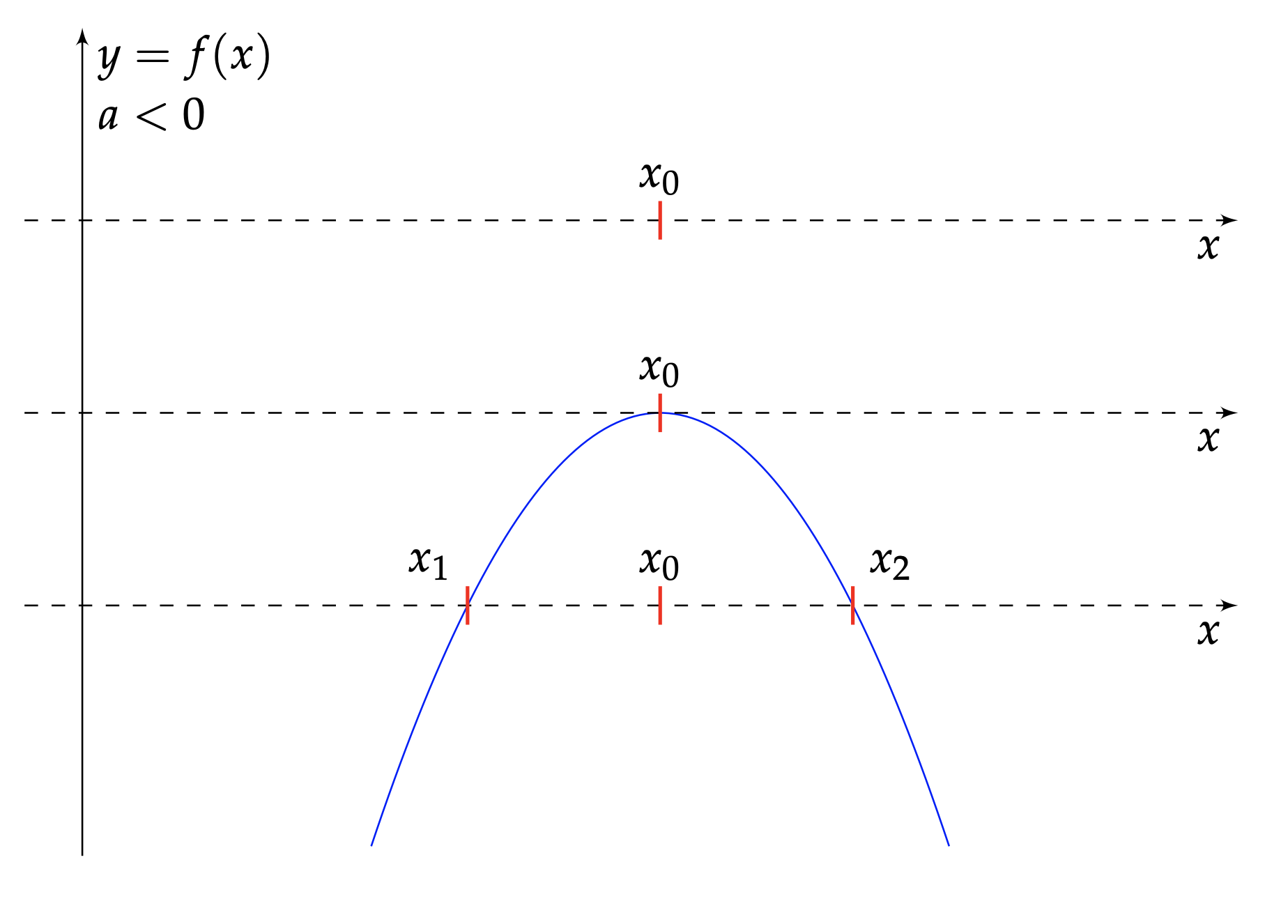
$a\lt 0$. Trois positions sont ici représentées, selon que la parabole traverse, tangente ou évite l’axe des abscisses (qui apparaît en pointillés).
Discriminant $\Delta$ et discussion. Le paragraphe précédent permet, à lui seul, de faire émerger la quantité $\Delta$ et d'en donner l'usage. En effet, pour que la branche parabolique traverse l'axe des abscisses, il faut et il suffit que l'extremum $f(x_0)$ et le coefficient $a$ soient en opposition de signe, soit : $$ f(-\frac{b}{2a}) \times a \lt 0, $$ ou encore $$ (-\frac{b^2}{4a} +c)\times a \lt 0, $$ qui revient à $$ b^2-4ac\gt 0. $$ Le cas échéant $f$ possède deux racines $x_1$ et $x_2$, une à gauche strictement de $x_0$, l'autre à droite, figures 2 et 3.
Axe de symétrie, somme et produit des racines. Dès l'instant que les pentes de $f$ se répondent de part et d'autre et à égale distance de $x_0$, il est assez concevable que le tracé de $f$ y gagne une symétrie axiale, figures 2 et 3. L'argument est certes heuristique, mais il peut suffire à convaincre dans un premier temps. Moyennant la condition $\Delta>0$, les deux racines mises en évidence ci-dessus ont donc exactement pour milieu $x_0$. Ainsi, $$ x_1+x_2 = -\frac{b}{a}. $$ Le produit peut, lui, tomber de différentes manières. Via une factorisation par exemple, suivie d'un développement et d'un principe d'identification — ce qui nécessite malgré tout quelques prérequis, ou tout simplement en retranchant à l'égalité $a x_1^2+b x_1 +c = 0$ pondérée de $x_2$ son égalité jumelle $a x_2^2+b x_2 +c = 0$ pondérée de $x_1$. En résulte $$ x_1 x_2 = \frac{c}{a}. $$
Racines. La somme de $x_1$ et $x_2$ une fois déterminée, il est naturel d'introduire la variable auxiliaire $u$, qui mesure un écart à la moyenne, en posant 17 : $$ x_1 = \frac{-b}{2a}-u \text{ et } x_2 = \frac{-b}{2a}+u. $$ Du reste, on peut exiger de $u$ d'avoir le signe de $a$ ; ceci ordonnera $x_1$ et $x_2$. Voilà qui, associé à la connaissance du produit $x_1 x_2$, fournit l'identité $$ x_1 x_2 = \frac{b^2}{4 a^2}-u^2 = \frac{c}{a}. $$ Dès lors, $$ u^2 = \frac{\Delta}{4a^2}, $$ donc $$ u = \frac{\sqrt{\Delta}}{2a} $$ et la boucle est bouclée puisqu'on retombe ainsi sur les célèbrissimes formules... $$ x_1 = \frac{-b+\sqrt{\Delta}}{2a}\text{ et } x_2 = \frac{-b-\sqrt{\Delta}}{2a} $$ ... enfin aux exceptions près pour lesquelles il y a moyen d'accélérer, telles les équations $x^2-a^2=0$, $x^2-2ax=0$ ou $x^2 \pm 2ax +a^2=0$ où $a$ est un réel donné.




