$\Pi.\!\Sigma.$ I love you (The Beatles, 1962)
En classe de première et à titre d'approfondissement 1, on a coutume de traiter par le second degré le système à deux inconnues $x$ et $y$ dont la somme $\Sigma$ et le produit $\Pi$ sont donnés. Soit : \begin{equation} \label{s} \left\{ \begin{aligned} x+y &=\Sigma \\ xy &=\Pi \end{aligned} \right. \end{equation}
Quand $\Pi$ est non nul2, on remonte ainsi (\ref{s}) en substituant $\frac{\Pi}{x}$ à $y$. Ceci mène à l'équation en $X$ satisfaite par $x$ (mais aussi par $y$) : \begin{equation} X^2-\Sigma X + \Pi = 0. \end{equation} Puis on résout habituellement en passant par le discriminant $\Delta = \Sigma^2-4\Pi.$
Il est aussi possible, et fructueux, d'adopter une autre logique. Si la somme $\Sigma$ de $x$ et de $y$ est connue, leur moyenne $\frac{\Sigma}{2}$ l'est aussi et se trouve en leur milieu. Dès lors est-il naturel d'écrire \begin{equation} x = \frac{\Sigma}{2}-u \text{ et } y = \frac{\Sigma}{2}+u \end{equation} où $u$ désigne une variable auxiliaire. Si bien que \begin{equation} \label{prod} xy = \Big(\frac{\Sigma}{2}\Big)^2-u^2=\frac{\Sigma^2}{4}-u^2=\Pi \end{equation} et donc \begin{equation} \label{delta} u^2 = \frac{1}{4}(\Sigma^2-4\Pi)=\frac{\Delta}{4}, \end{equation} qui renoue avec la traditionnelle discussion sur le signe de $\Delta$, d'où les valeurs potentielles de $u$, et consécutivement du couple $(x,y)$ .
Cette méthode ne requiert aucune connaissance préalable et tiendrait du miracle sans son interprétation géométrique. Sous réserve que $x$ et $y$ soient positifs, identifions-les aux côtés d'un rectangle, figure 1. Ainsi, $x+y = \Sigma$ mesure un demi-périmètre et $xy = \Pi$, une aire.
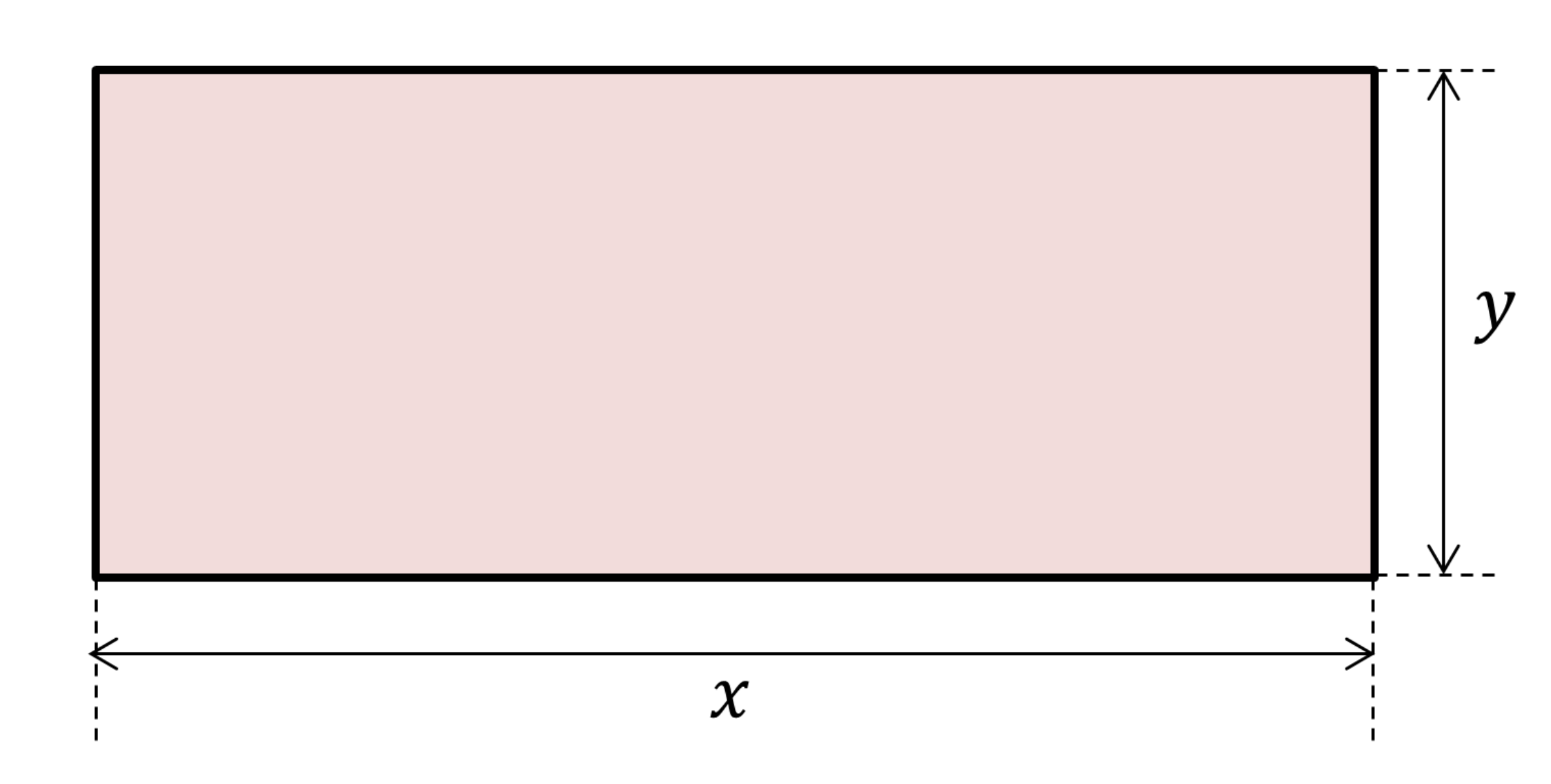
Tout d'abord, la relation (\ref{prod}) entre $\Sigma$, $\Pi$ et $u$ prend tout son sens, comme l'illustre la figure 2.
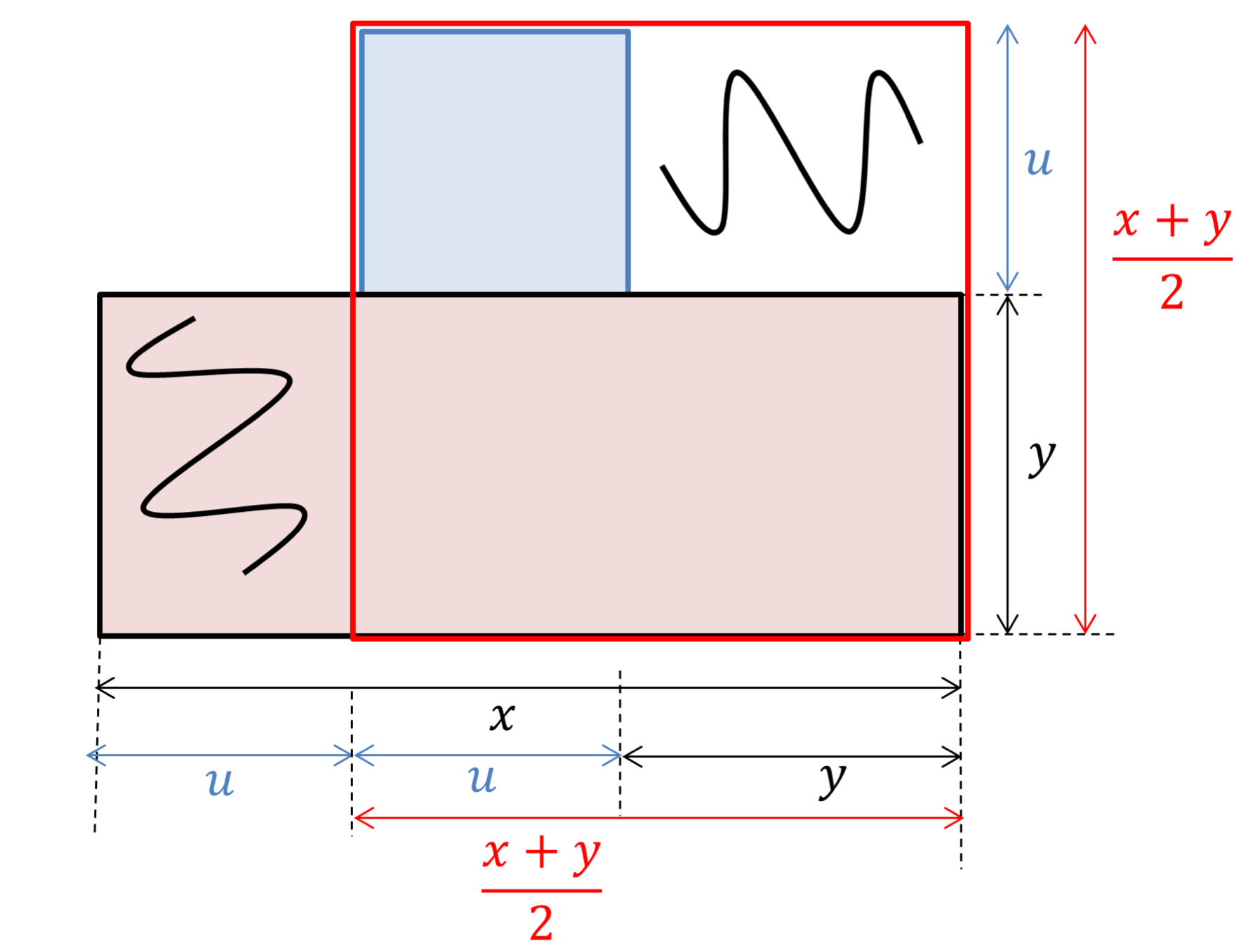
En ré-agençant les deux petits rectangles, on reconstitue le grand rectangle mauve. En passant aux aires, on retrouve : $\Big( \frac{x+y}{2} \Big)^2 = u^2 + xy$, soit $\frac{\Sigma^2}{4} =u^2+\Pi.$
Puis on anticipe l'impasse à laquelle peut conduire l'équation (\ref{delta}). Car on devine qu'à périmètre fixé, l'aire sera matériellement contrainte. Donc qu'au delà d'une certaine borne, la valeur de $\Pi$ ne sera plus conciliable avec celle de $\Sigma$. De fait, assez grossièrement, \[ x+y=\Sigma \Rightarrow x,y \leq \Sigma \Rightarrow xy=\Pi\leq\Sigma^2, \] et plus précisément, à l'aide de (\ref{prod}), \[ x+y=\Sigma \Rightarrow xy = \Pi \leq \frac{\Sigma^2}{4}. \]
À l'inverse, on ne s'attend pas à ce qu'une aire fixée limite le périmètre : écraser le rectangle tout en l'étirant ouvre le jeu.
Enfin, on comprend qu'à périmètre fixé le carré réalise, parmi les rectangles, la plus grande aire et que de manière duale, à aire fixée, le même carré réalise le plus petit périmètre. Le fait est, toujours via (\ref{prod}), \[ x+y=\Sigma \Rightarrow xy \leq \frac{\Sigma^2}{4} \] avec égalité si, et seulement si, $u=0$. Et \[ xy=\Pi \Rightarrow \frac{\Sigma^2}{4} \geq \Pi \Rightarrow \Sigma \geq 2 \sqrt{\Pi} \] avec égalité si, et seulement si, $u=0$.







