Une marche aléatoire est un modèle mathématique issu de la théorie des Probabilités. Elle est composée d'une succession de pas effectués de manière aléatoire, généralement sans lien avec les pas précédents.
►Pour la classe : Activité : La marche du crabe.
Le modèle
On appelle marche aléatoire sur $\mathbb{Z}$ le modèle mathématique décrit de la manière suivante. À l'instant $n=0$, un crabe se trouve à l'origine (le point $0$ de la droite des entiers relatifs). Aux instants suivants, il peut se déplacer en allant à droite avec probabilité $p$ ou à gauche avec probabilité $1-p$ indépendamment des déplacements précédents. On peut s'intéresser à l'évolution de la position du crabe dans le temps ou encore à la probabilité qu'il a de revenir à l'origine.
Soit $S_n$ la position du crabe à l'instant $n$ et $X_k$ la variable qui décrit le $k$-ième pas, c'est-à-dire pour $k\geq1$
$$X_k = \left\{
\begin{array}{rlc} +1 & \text{avec probabilité}& p \\
-1 & \text{avec probabilité}& 1-p \end{array}\right.$$
où $+1$ correspond au fait d'aller à droite et $-1$ à celui d'aller à gauche. On a alors pour $n\geq0$ la relation suivante
$$S_{n+1} = S_n + X_{n+1} = \sum_{k=1}^{n+1}X_k.$$
On peut rapprocher $(S_n)$ du schéma de Bernoulli et de la loi binomiale. En effet, soit $(Y_n)$ une suite de variables aléatoires de loi de Bernoulli de paramètre $p$ représentant par exemple les lancers successifs et indépendants d'une pièce (équilibrée ou non). On définit alors $F = \text{"obtenir face"}$ et $P=\text{"obtenir pile"}$, l'univers à l'instant $n$ est donc $\{F,P\}^n=\{0,1\}^n$ et on a
\begin{equation}
\tag{$\star$}
\label{etoile}
X_k = 2Y_k-1=\left\{
\begin{array}{rl} +1 & \text{si } Y_k = 1 \\
-1 & \text{si } Y_k= 0 \end{array}\right..
\end{equation}
Comme $T_n=\sum_{k=1}^n Y_k$ est la variable aléatoire représentant le nombre de succès après $n$ répétitions du lancer de pièce, $T_n$ suit une loi binomiale de paramètres $n$ et $p$. La relation ($\star$) implique que la loi position $S_n= 2T_n-n$ est fortement liée à la loi binomiale. Comme $\dfrac{T_n}{n}$ est la moyenne empirique de la suite $(X_k)$, la loi faible des grands nombres pour le schéma de Bernoulli assure que
$$\forall \varepsilon >0, \ \lim_{n\to\infty}\mathbb{P}\Big(\Big|\frac{T_n}{n}-p\Big|\geq\varepsilon\Big)=0$$
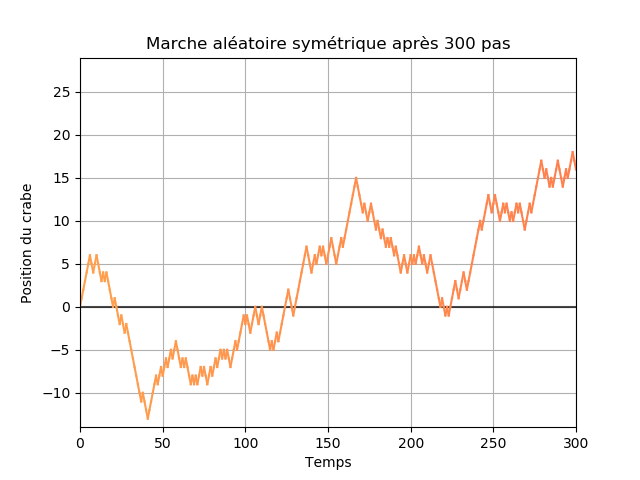
ce qui se dit $\dfrac{T_n}{n}$ converge en probabilité vers $p$. Il est alors possible d'en déduire que $\dfrac{S_n}{n}$ converge en probabilité vers $2p-1$. On peut interpréter ce résultat comme "$\dfrac{S_n}{n} \simeq 2p-1$" quand $n$ est grand et si $p\neq\dfrac{1}{2}$ on peut alors dire que "$S_n$ tend vers $+\infty$ ou $-\infty$" en un certain sens.
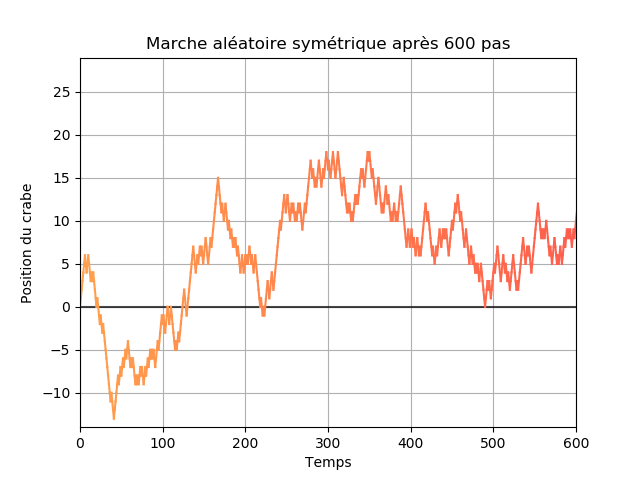
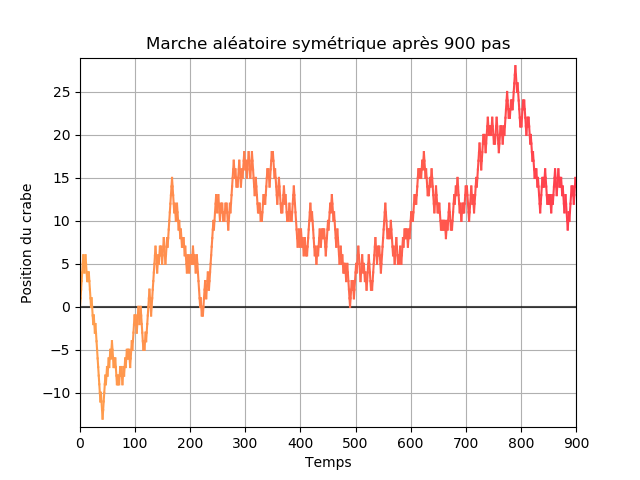
Sur l'image précédente et sur les suivantes les abscisses représentent le temps et les ordonnées la position du crabe. L'évolution au cours du temps est aussi représentée par la couleur, plus le bleu est foncé plus l'instant est grand.
En utilisant les images précédentes on peut s'intéresser au premier instant où le crabe dépasse un certain point $a$ ou arrive en dessous d'un autre point $b$ de la ligne $\mathbb{Z}$. Dans un autre contexte, ceci peut servir à représenter un joueur à un casino qui s'arrête soit dès qu'il a gagné plus que le montant $a$ soit dès qu'il lui reste moins que le montant $b$. Ce phénomène appelé la ruine du joueur est bien connu en Probabilités. Les calculs ne sont pas évidents mais il n'est pas compliqué de comprendre le problème avec les dessins précédents.
Marches aléatoires symétriques
La marche est dite symétrique lorsque $p=1/2$, cela revient à lancer une pièce équilibrée avant chaque pas pour décider. Le crabe a donc autant de chances de se déplacer vers la droite que vers la gauche. On peut s'intéresser à différentes choses à propos du crabe. Par exemple, est-ce qu'il peut retourner à l'origine à un instant $n$ ? Oui il peut et il est même presque sûr qu'il va y revenir. En moyenne, combien de temps met-il à revenir ? Un calcul assez compliqué montre que le temps de retour est infini en moyenne.
Dimension 2
Après beaucoup de temps à se déplacer sur une ligne horizontale, le crabe rencontre un autre crabe qui se déplace uniquement verticalement. Si l'un se place sur le dos de l'autre, ils découvrent qu'ils peuvent alors se déplacer dans les deux directions et parcourir toute la plage ! Le déplacement a donc lieu sur un quadrillage, comme $\mathbb{Z}^2$. On le modélise alors de la manière suivante : soit $(Z_n)$ et $(Y_n)$ deux suites de variables aléatoires indépendantes et qui représentent chacune les lancers de pièces équilibrées. La suite $(Z_n)$ va déterminer l'orientation (horizontale ou verticale) du déplacement du crabe à l'instant $n$, tandis que la suite $(Y_n)$ va déterminer le sens du déplacement. On a $S_n\in\mathbb{Z}^2$ et la position pour $n\geq 0$ est
\begin{equation*}
S_{n+1} = S_n + X_{n+1} = \begin{pmatrix} S_n^x \\ S_n^y\end{pmatrix}
+\begin{pmatrix} X_{n+1}^x \\ X_{n+1}^y\end{pmatrix}
\end{equation*}
où $X_{n+1}$ est donné par
\begin{equation}
\tag{$\star\star$}
\label{etoile2}
\hspace{-1em}X^x_{n} =\left\{
\begin{array}{rl} 0 & \text{si $Z_{n} = 0$} \\
+1 & \text{si $Z_{n}=1$ et $Y_n= 1$} \\
-1 & \text{si $Z_{n}=1$ et $Y_n= 0$} \end{array}\right. \quad\text{et}\quad
X^y_{n+1} =\left\{
\begin{array}{rl}
0 & \text{si $Z_{n}=1$} \\
+1 & \text{si $Z_{n}=0$ et $Y_n= 1$}\\
-1 & \text{si $Z_{n}=0$ et $Y_n= 0$}\end{array}\right..
\end{equation}
Nous allons commencer par vérifier que la probabilité d'aller dans une des quatre directions possibles est $p=1/4$. À l'aide de $(\star\star)$ et par indépendance de $Z_n$ et $Y_n$ on obtient bien
\begin{equation*}
\mathbb{P}(X_n^x = +1)= \mathbb{P}(Z_n=1)\mathbb{P}(Y_n=1)= \frac{1}{2}\times\frac{1}{2} = \frac{1}{4}.
\end{equation*}
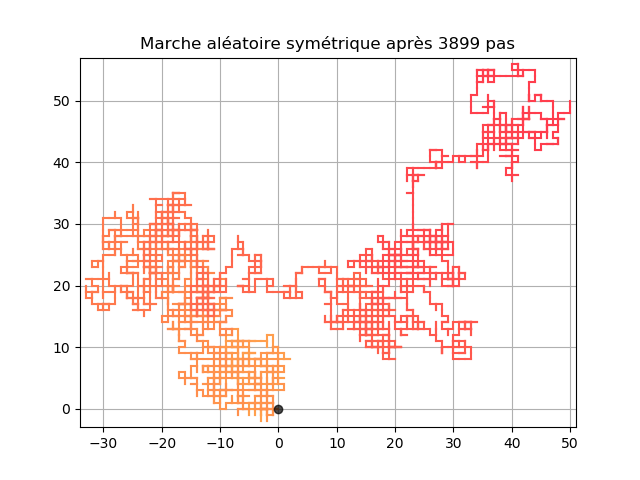
On peut ensuite se poser les mêmes questions que précédemment. Est-ce qu'il peut retourner à l'origine à un instant $n$ ? Oui, il peut toujours. En moyenne, combien de temps met-il à revenir ? La moyenne n'est pas finie, donc on ne le voit pas forcément en pratique car il faut attendre trop longtemps. Dans ce cas la probabilité de retour en l'origine en temps fini est aussi égale à 1, mais le temps moyen de retour en l'origine est très grand. On dit alors que la marche est récurrente nulle.
Sur l'image précédente et sur les suivantes l'évolution de la position (en 2D) du crabe au cours du temps est donnée par la couleur du point, plus elle est foncée plus l'instant est grand.
Dimension 3 ou supérieure
Soit $d\geq3$, alors la marche symétrique correspond au cas où la probabilité d'aller dans une des $2d$ directions est $p=1/(2d)$. Pour le cas $d=3$, puisque les crabes ne volent pas, on peut imaginer un oiseau qui se déplace. On peut encore se poser les mêmes questions. Est-ce qu'il peut retourner à l'origine à un instant $n$ ? Cette fois-ci la réponse est non, pas forcément. Dans ce cas la probabilité de retour en l'origine en temps fini est strictement inférieure à 1. On peut voir ici l'influence des directions : il y a trop de possibilités.
Mouvement brownien
En 1827, le botaniste Robert Brown a remarqué qu’en disposant des particules de pollen dans un milieu liquide, celles-ci se déplaçaient selon des trajectoires aléatoires et non prévisibles. Ces trajectoires, notamment dues aux chocs entre les particules, seront appelées mouvement brownien. En regardant le comportement du mouvement brownien entre deux instants très proches on observe quelque chose qui ressemble à une marche aléatoire. On s'attend donc à ce que les deux modèles aient un comportement similaire, et effectivement cela se vérifie bien mathématiquement. Outre les trajectoires du pollen, on retrouve le mouvement brownien ailleurs : les pingouins se collent les uns aux autres sur la banquise pour se tenir chaud, et le grand nombre de pingouins provoque de multiples chocs du fait du sol glissant de la banquise. Ainsi, le déplacement d'un pingouin serait en fait un mouvement brownien !