Connaissez-vous la fonction cardinale de Whittaker père et fils1 ? ... baptisée ainsi, car considérée comme une fonction essentielle. On a fait dire à Whittaker2 que cette fonction est...

On la connait aujourd'hui principalement sous le nom de sinus cardinal (en abrégé « sinc ») à cause de la fonction sinus intervenant dans sa définition. Il s'agit en effet de la fonction $$ \frac{\sin x}{x} $$ qui est bien connue aujourd'hui dans de nombreux domaines des mathématiques et de la physique, sans oublier les sciences de l'ingénieur : analyse de Fourier, optique ondulatoire, traitement du signal ; elle a aussi des liens avec l'analyse complexe et les fonctions zêta et gamma. Le résultat emblématique qui fait intervenir le fameux et glorieux sinus cardinal est aujourd'hui connu sous le nom de théorème d'échantillonnage3. C'est Whittaker père qui a donné l'essentiel de la preuve sous forme de théorème d'interpolation et Whittaker fils qui a poursuivi et amélioré ses travaux.

L'intégrale de Dirichlet

Mais le sinus cardinal recèle de nombreux trésors et curiosités. À commencer par l'intégrale $$ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \,\mathrm{d} x = \pi $$ parfois appelée intégrale de Dirichlet (nous verrons plus tard comment la calculer).

Les intégrales de Borwein : une généralisation de l'intégrale de Dirichlet ?

Partant de l'égalité $\int_{-\infty}^{+\infty} \frac{\sin x}{x} \,\mathrm{d} x = \pi$, intéressons-nous à la suite des intégrales $\int_{-\infty}^{+\infty} \frac{\sin x}{x} \; \frac{\sin (x/3)}{x/3} \,\mathrm{d} x$, $\int_{-\infty}^{+\infty} \frac{\sin x}{x} \; \frac{\sin (x/3)}{x/3} \; \frac{\sin (x/5)}{x/5} \,\mathrm{d} x$, etc. où à chaque étape on incorpore un nouveau sinus cardinal sous l'intégrale. En calculant les premières valeurs, on trouve : \begin{align*} \int_{-\infty}^{+\infty} \frac{\sin x}{x} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \frac{\sin (x/5)}{x/5} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \frac{\sin (x/5)}{x/5} \frac{\sin (x/7)}{x/7} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \frac{\sin (x/5)}{x/5} \frac{\sin (x/7)}{x/7} \frac{\sin (x/9)}{x/9} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \frac{\sin (x/5)}{x/5} \frac{\sin (x/7)}{x/7} \frac{\sin (x/9)}{x/9} \frac{\sin (x/11)}{x/11} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty} \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \frac{\sin (x/5)}{x/5} \frac{\sin (x/7)}{x/7} \frac{\sin (x/9)}{x/9} \frac{\sin (x/11)}{x/11} \frac{\sin (x/13)}{x/13} \mathrm{d} x &= \pi\\ \int_{-\infty}^{+\infty}\!\! \frac{\sin x}{x} \frac{\sin (x/3)}{x/3} \frac{\sin (x/5)}{x/5} \frac{\sin (x/7)}{x/7} \frac{\sin (x/9)}{x/9} \frac{\sin (x/11)}{x/11} \frac{\sin (x/13)}{x/13} \frac{\sin (x/15)}{x/15} \mathrm{d} x &= \text{?} \end{align*} Intuitivement, on a envie de dire que ce ne peut pas être un hasard, et qu'il y a là une formule générale. Toutes ces intégrales ne peuvent pas valoir autre chose que $\pi$. Deux solutions s'offrent à nous :

• prendre son courage à deux mains et chercher sans attendre une démonstration générale (on cherche toujours !)
• calculer de plus en plus de termes à l'aide de logiciels de calcul formel, pour affermir sa croyance avant de poursuivre (à condition que le logiciel soit fiable !)

Pour cette deuxième solution, on peut par exemple utiliser le logiciel Sage en allant sur la page https ://sagecell.sagemath.org et en tapant les instructions suivantes pour vérifier les premières valeurs :

from sage.symbolic.integration.integral import definite_integral as integral 
[ integral(sin(x)/x,x,-Infinity,Infinity), 
  integral((sin(x)/x)*(sin(x/3)/(x/3)),x,-Infinity,Infinity), 
  integral((sin(x)/x)*(sin(x/3)/(x/3))*(sin(x/5)/(x/5)),x,-Infinity,Infinity), 
  integral((sin(x)/x)*(sin(x/3)/(x/3))*(sin(x/5)/(x/5))*(sin(x/7)/(x/7)),x,-Infinity,Infinity), 
  integral((sin(x)/x)*(sin(x/3)/(x/3))*(sin(x/5)/(x/5))*(sin(x/7)/(x/7))*
           (sin(x/9)/(x/9)),x,-Infinity,Infinity), 
  integral((sin(x)/x)*(sin(x/3)/(x/3))*(sin(x/5)/(x/5))*(sin(x/7)/(x/7))*
           (sin(x/9)/(x/9))*(sin(x/11)/(x/11)),x,-Infinity,Infinity), 
  integral((sin(x)/x)*(sin(x/3)/(x/3))*(sin(x/5)/(x/5))*(sin(x/7)/(x/7))*
           (sin(x/9)/(x/9))*(sin(x/11)/(x/11))*(sin(x/13)/(x/13)),x,-Infinity,Infinity)]

La réponse est :

[pi, pi, pi, pi, pi, pi, pi]

Tout va bien ! Le logiciel Sage semble bien capable de calculer formellement ces intégrales. Calculons donc le terme suivant :

integral((sin(x)/x)*(sin(x/3)/(x/3))*(sin(x/5)/(x/5))*(sin(x/7)/(x/7))*
         (sin(x/9)/(x/9))*(sin(x/11)/(x/11))*(sin(x/13)/(x/13))*(sin(x/15)/(x/15)),x,-Infinity,Infinity)

La réponse se fait attendre... et finalement, le couperet tombe :

467807924713440738696537864469/467807924720320453655260875000*pi 

C'est à dire $$ \frac{467807924713440738696537864469}{467807924720320453655260875000}\pi =0.9999999999852937186\ldots \pi $$ donc pas tout-à-fait $\pi$, bien que très proche ! A-t-on dépassé les limites de calcul ou y a-t-il un bug dans le logiciel ? David et Jonathan Borwein, père et fils, qui ont étudié ces intégrales en 2001, rapportent cette mésaventure :

Qu'en est-il vraiment ? C'est ce que nous allons voir !

Les outils

Pour résoudre ce mystère, il nous faut des outils. L'outil principal est ici la transformée de Fourier. C'est un choix logique car on a affaire à des intégrales de fonctions sinusoïdales, et à des produits de fonctions.

Plusieurs notations sont utilisées pour la transformée de Fourier, selon les usages et les communautés. La meilleure notation pour notre problème sera celle des ingénieurs5 : la transformée de Fourier $\hat{f}(x)$ de la fonction $f(t)$ (fonction du temps) est notée $$ \hat{f}(x) = \int_{-\infty}^{+\infty} f(t) e^{-2i\pi x t} \,\mathrm{d} t $$ où $x$ est un paramètre de fréquence6.

L'intérêt de la transformation de Fourier est de changer complètement de perspective, sans perte d'information : on peut toujours revenir ensuite à l'espace initial des signaux par transformée de Fourier inverse, définie par7 $$ f(t) = \int_{-\infty}^{+\infty} \hat{f}(x) e^{2i\pi x t} \,\mathrm{d} x $$ Dans notre cas, la transformée de Fourier va surtout nous permettre de transformer le produit des fonctions sinus cardinaux en produit de convolution de fonctions plus simples.

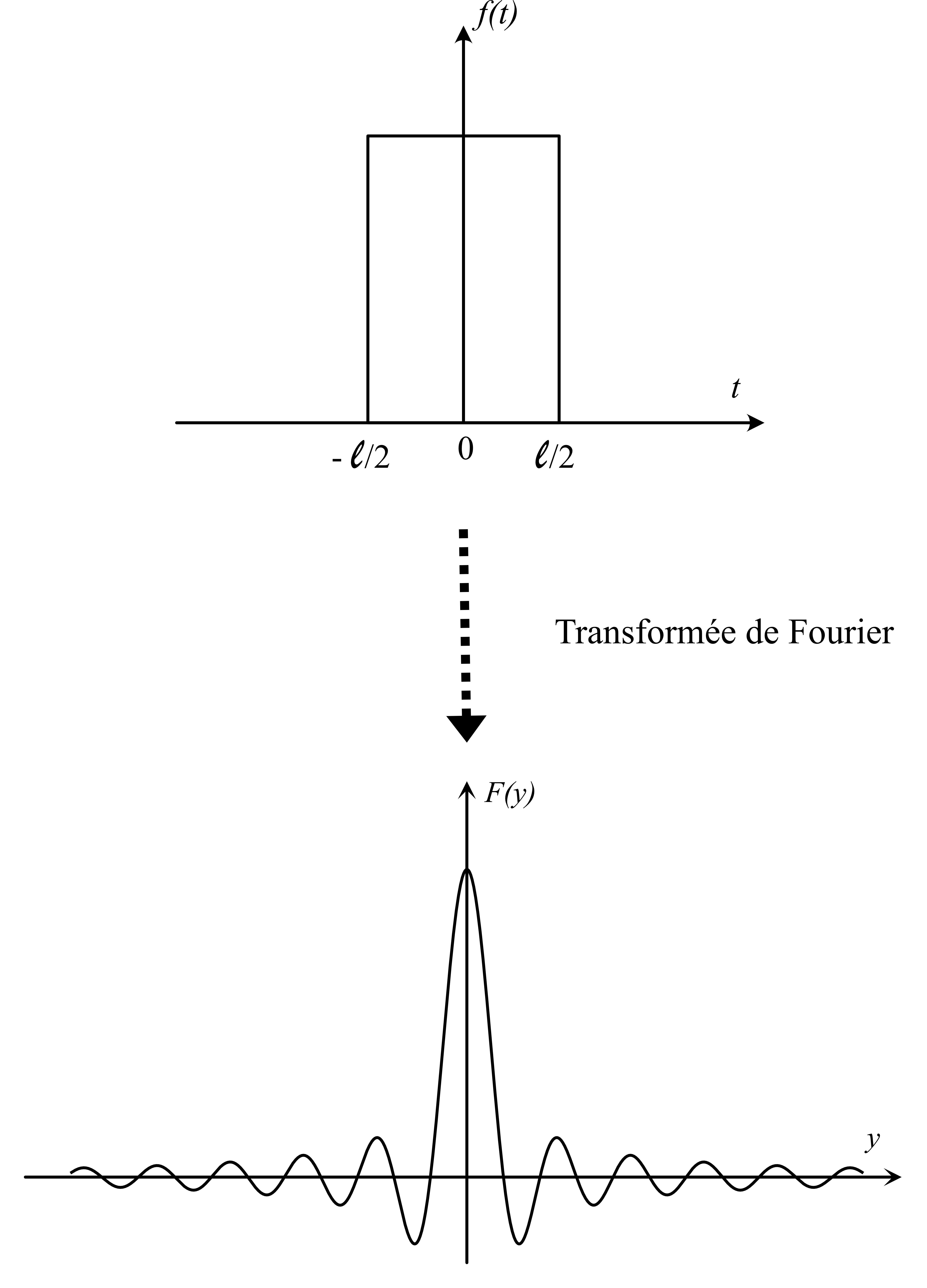
Quoi de plus simple qu'une fonction « porte » ?

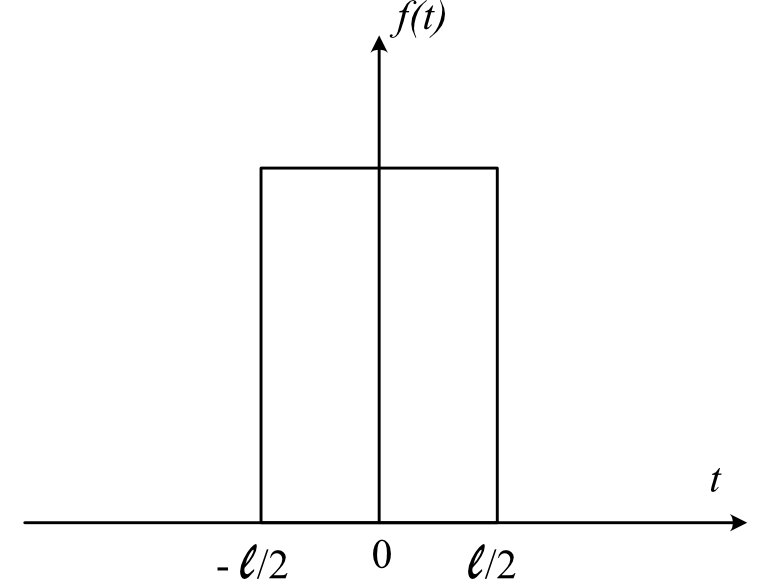
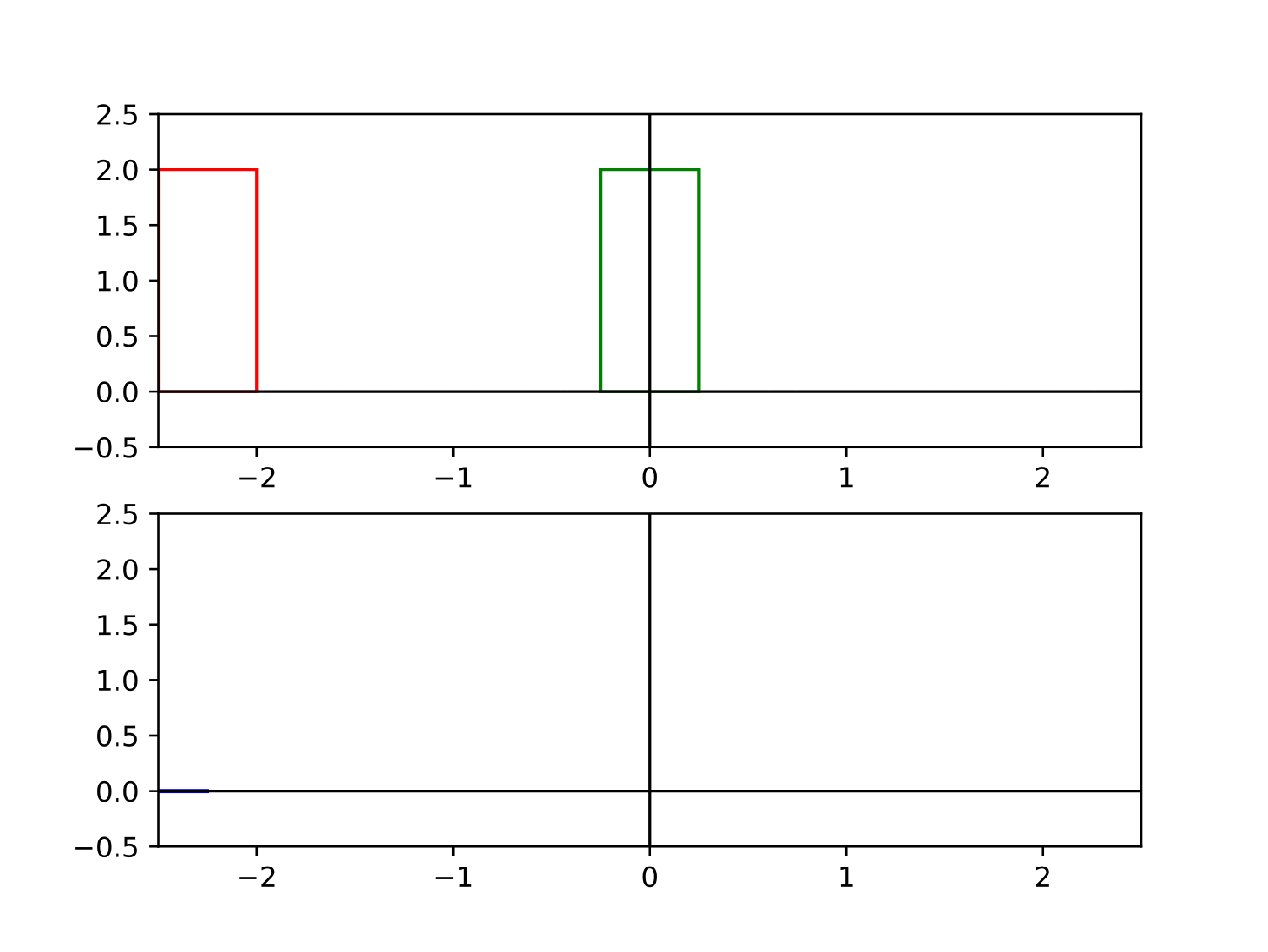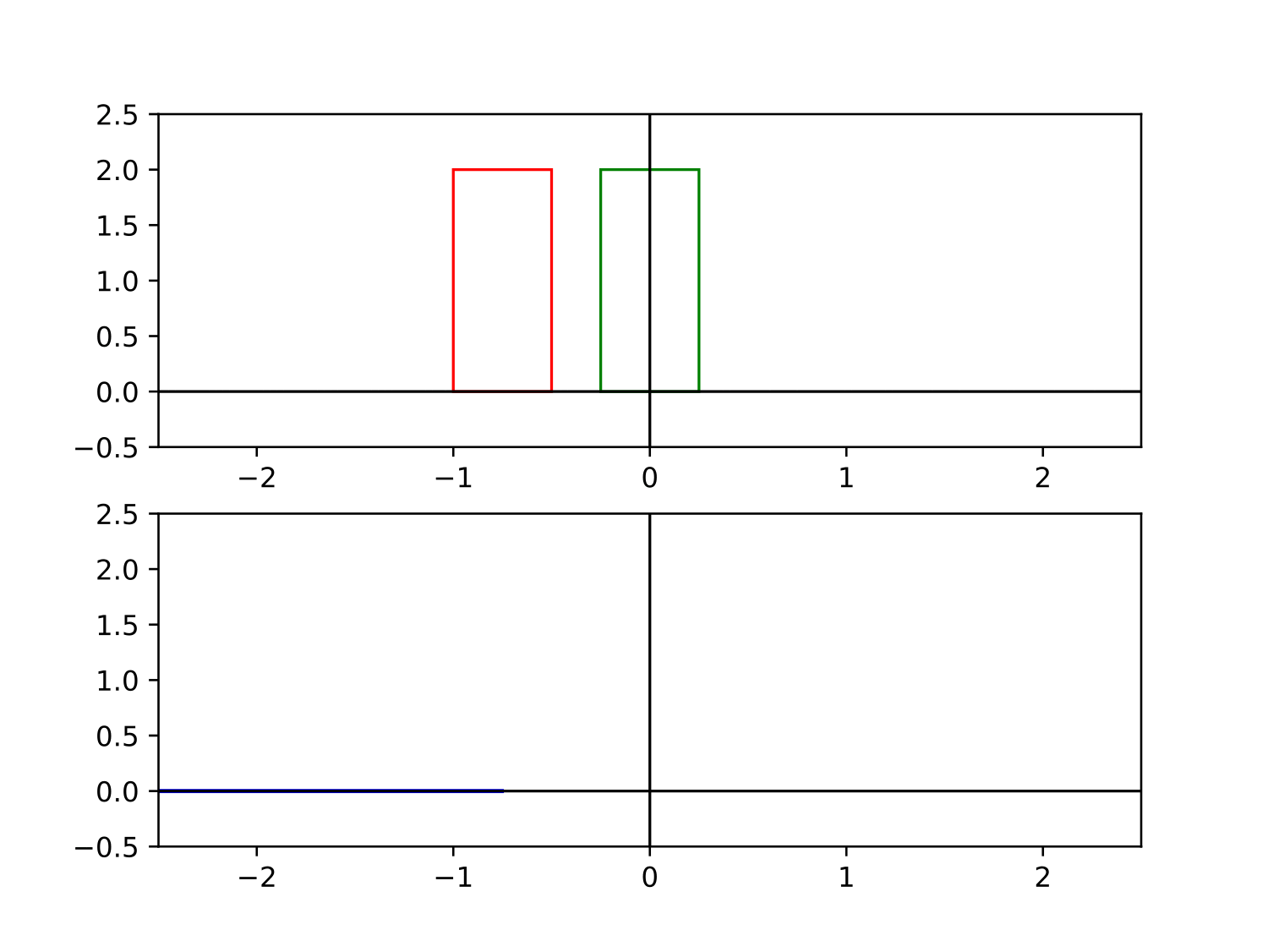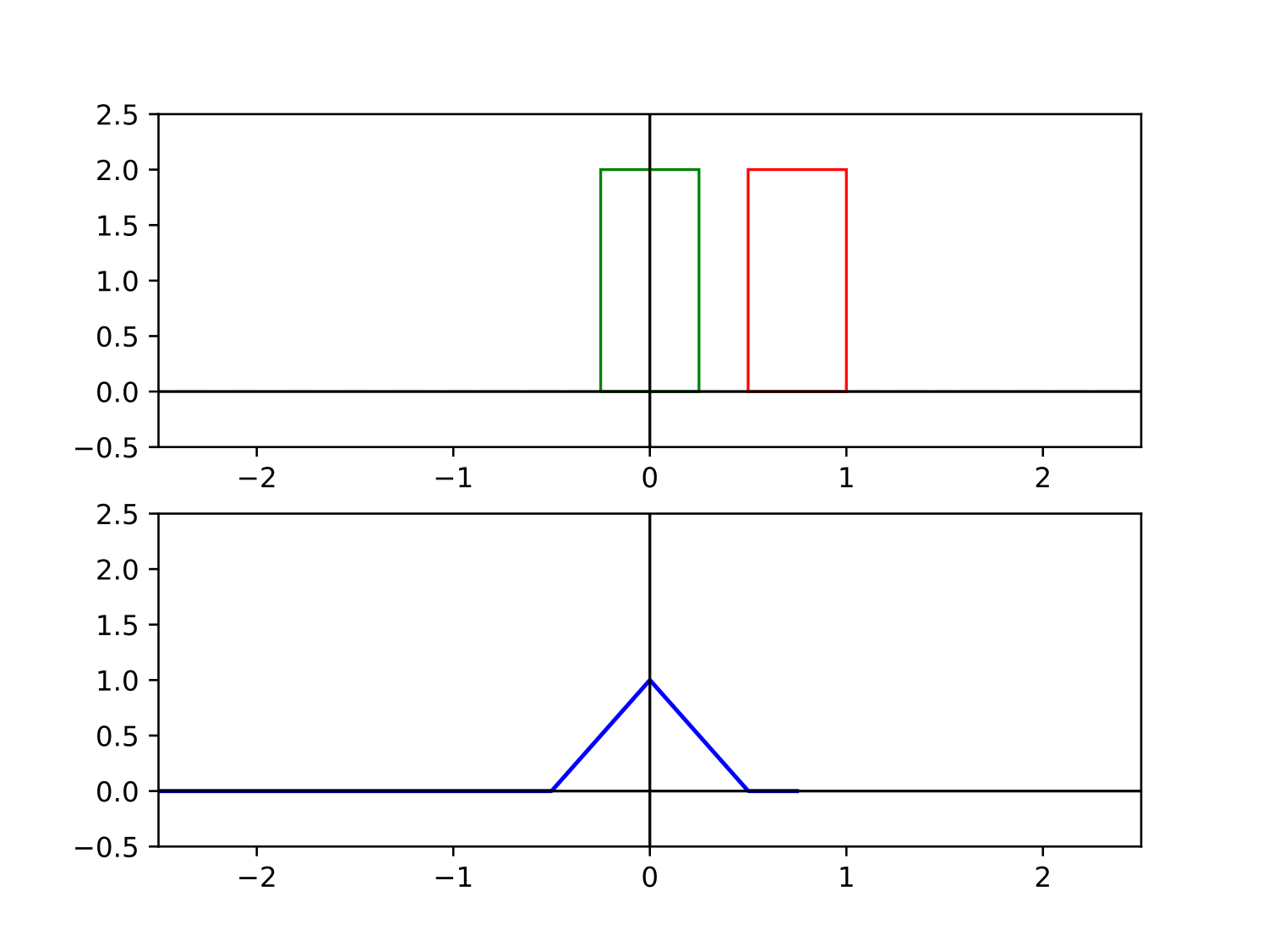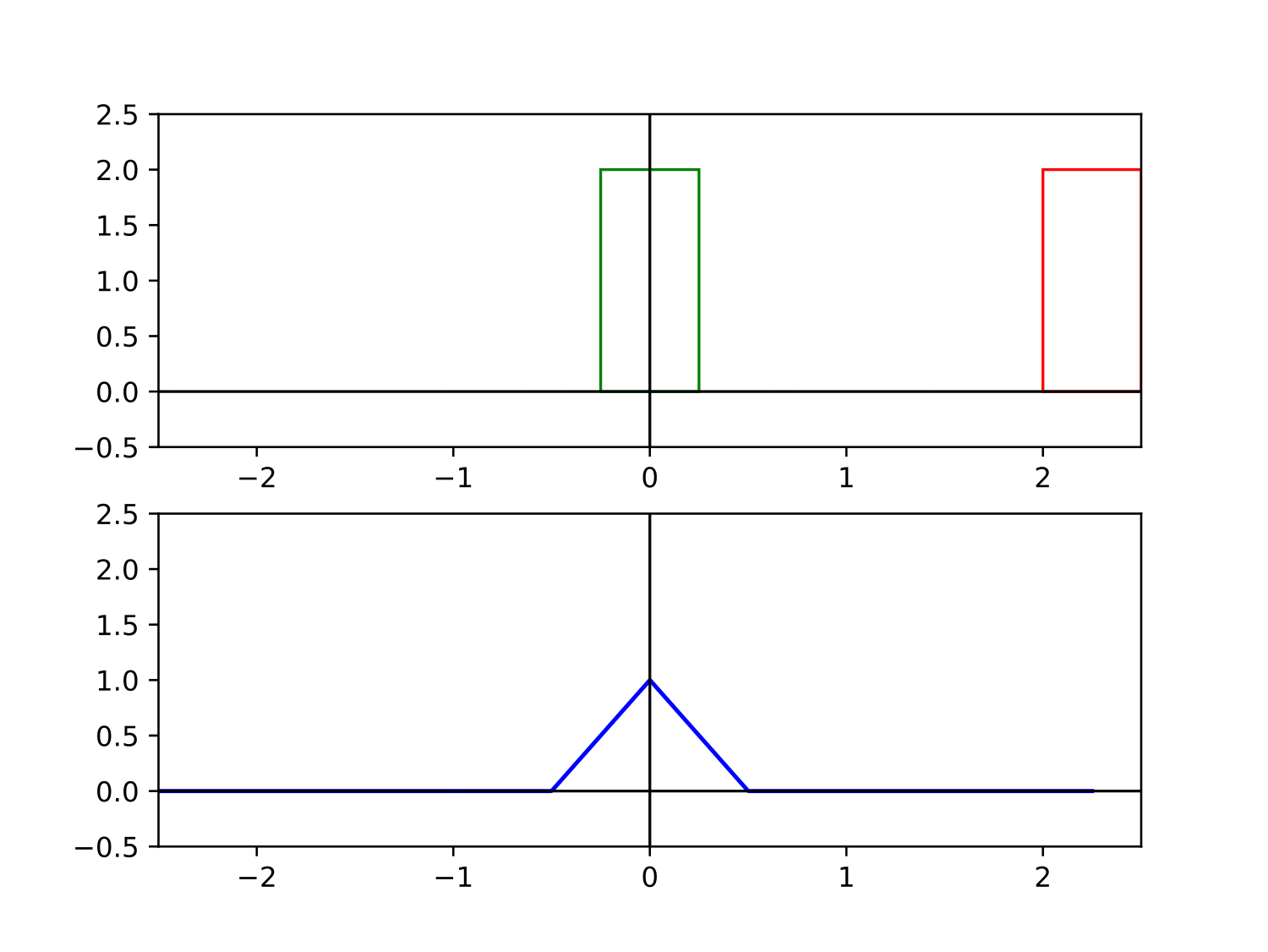
Pour illustrer graphiquement le produit de convolution, prenons-en une de largeur $\ell$ : 8 $$ \Pi_\ell (t) = \frac{1}{\ell}\times\left\{ \begin{aligned} 1 &\quad \text{si $|t|<\ell/2$}\\ 0 &\quad \text{sinon} \end{aligned}\right. $$ Son produit de convolution avec elle-même est illustré ci-dessous. On obtient une fonction triangle qu'on notera $\Lambda$ par la suite.

Sa transformée de Fourier se calcule facilement9 : \begin{align*} \hat{\Pi}_\ell (x) &= \frac{1}{\ell}\times \int_{-\ell/2}^{+\ell/2} e^{-2i\pi x t} \,\mathrm{d} t\\ &=\frac{1}{\ell}\times \Bigl[ \frac{e^{-2i\pi x t}}{-2i\pi x} \Bigr]_{-\ell/2}^{+\ell/2}\\ &=\frac{1}{\ell}\times \frac{e^{i\pi x \ell}-e^{-i\pi x \ell}}{2i\pi x} \\ &=\frac{\sin(\pi \ell x)}{\pi \ell x}. \end{align*} On reconnait notre sinus cardinal !

Profitons-en pour adopter une notation qui nous permettra de simplifier l'écriture : $$ \mathrm{sinc} x = \frac{\sin\pi x}{\pi x} $$ avec la convention $\mathrm{sinc} (0)=1$ (prolongement par continuité). Ainsi

Par un petit changement de variable, les intégrales de Borwein qui nous intéressent deviennent : \begin{align*} \int_{-\infty}^{+\infty}\mathrm{sinc} x\,\mathrm{d} x &= 1\\ \int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\,\mathrm{d} x &= 1\\ \int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\;\mathrm{sinc}\frac{x}5\,\mathrm{d} x &= 1\\ &\vdots\\ \int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\;\mathrm{sinc}\frac{x}5\;\mathrm{sinc}\frac{x}7\; \mathrm{sinc}\frac{x}9\;\mathrm{sinc}\frac{x}{11}\;\mathrm{sinc}\frac{x}{13}\,\mathrm{d} x &= 1\\ \int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\;\mathrm{sinc}\frac{x}5\;\mathrm{sinc}\frac{x}7\;\mathrm{sinc}\frac{x}9\;\mathrm{sinc}\frac{x}{11}\;\mathrm{sinc}\frac{x}{13}\;\mathrm{sinc}\frac{x}{15} \,\mathrm{d} x &=\,\text{?} \end{align*}

Nous avons à présent tout ce qu'il faut pour calculer ces intégrales. La première, l'intégrale de Dirichlet, est un cas un peu spécial que nous allons traiter séparément.

Calcul de l'intégrale de Dirichlet

Si le sinus cardinal était absolument intégrable, on pourrait procéder comme suit. Par la formule d'inversion de Fourier, comme $\mathrm{sinc}$ est la transformée de Fourier d'une porte centrée de largeur $1$, on aurait : $$ \Pi_1(t) = \int_{-\infty}^{+\infty} \mathrm{sinc}(x) e^{2i\pi x t} \,\mathrm{d} x $$ En particulier en $t=0$ : $$ \int_{-\infty}^{+\infty} \mathrm{sinc} x \,\mathrm{d} x =\Pi_1(0) = 1 $$ ce qui donne bien $$ \int_{-\infty}^{+\infty} \frac{\sin x}{x}\,\mathrm{d} x = \pi. $$ Malheureusement, $\mathrm{sinc} x$ n'est pas absolument intégrable. Cependant, son carré $\mathrm{sinc}^2 x$ l'est. Or, nous avons montré dans l'encadré ci-dessus l'égalité $$ \int_{-\infty}^{+\infty} \mathrm{sinc} x \,\mathrm{d} x =\int_{-\infty}^{+\infty} \mathrm{sinc}^2\!x\, \,\mathrm{d} x $$ Cette fois-ci, avec la même idée en appliquant la formule d'inversion de Fourier, nous obtenons $$ \int_{-\infty}^{+\infty} \mathrm{sinc}^2\!x\, \,\mathrm{d} x =\Pi_1\ast\Pi_1(0)=\Lambda(0)=1 $$ où $\Lambda$ est la fonction triangle de hauteur 1 et de demi-largeur 1 (voir la figure ci-dessus d'illustration graphique du produit de convolution). On obtient bien le résultat : $$ \int_{-\infty}^{+\infty} \frac{\sin x}{x}\,\mathrm{d} x = \pi. $$

Calcul des autres intégrales de Borwein

Pour toutes les intégrales de Borwein suivantes, les produits de sinus cardinaux sont des fonctions absolument intégrables. On peut donc utiliser directement la formule d'inversion de Fourier. Cette méthode astucieuse a été proposée par H. Schmid en 2014.

Comme précédemment, par la formule d'inversion de Fourier et le théorème de convolution en $t=0$, on obtient $$ \int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\cdots \mathrm{sinc}\frac{x}{2N+1} \,\mathrm{d} x = \Pi_1 \ast \Pi_{\frac{1}{3}} \ast\cdots\ast \Pi_{\frac{1}{2N+1}}(0) $$ où on a utilisé que $\mathrm{sinc}(\ell x)$ est la transformée de Fourier de la porte $\Pi_\ell(t)$.

L'avantage de cette méthode est qu'elle possède une interprétation graphique particulièrement éclairante. En effet, si on représente graphiquement les produits de convolution successifs de portes de plus en plus étroites, on obtient les étapes suivantes (voir la figure) :

• $\Pi_1$ a un plateau central de hauteur $1$ de largeur $1$
• $\Pi_1 \ast \Pi_{\frac{1}{3}}$ a un plateau central de hauteur $1$ de largeur $1-\frac{1}{3}$
• $\Pi_1 \ast \Pi_{\frac{1}{3}} \ast \Pi_{\frac{1}{5}}$ a un plateau central de hauteur $1$ de largeur $1-\frac{1}{3}-\frac{1}{5}$
• etc.
  • Le plateau central de hauteur 1 perdure tant que $$ 1-\frac{1}{3}-\frac{1}{5}-\cdots-\frac{1}{2N+1} >0 $$ Comme la série harmonique $\frac{1}{3}+\frac{1}{5}+\cdots$ tend vers $+\infty$, il y a forcément un plus grand entier impair vérifiant cette inégalité. On trouve numériquement que c'est $2N+1=13$.

     

    Par conséquent, à partir de $2N+1=15$, le plateau central disparait, le « tas de neige fond »10 et la hauteur centrale diminue (elle devient $\lt 1$). Ce qui explique le phénomène.

    Quelques Variantes Amusantes

    C'est donc la divergence de la série harmonique qui provoque le phénomène : le plateau finit par disparaître, on passe d'une valeur $=1$ en $t=0$ à une valeur $\lt 1$. À partir de là, il est facile de trouver d'autres variations sur le même thème :

    Une suite d'intégrales similaires qui reste constante encore plus longtemps

    La suite des intégrales de Borwein ne décroche qu'au huitième terme. Pour décrocher encore plus loin, suivant une suggestion de H. Schmid, partons de $$ 2\mathrm{sinc} 2x = 2\frac{\sin 2\pi x}{2\pi x} =2\frac{2\cos \pi x\sin \pi x}{2\pi x} =2 \cos \pi x \mathrm{sinc} x $$ au lieu de $\mathrm{sinc} x$, pour que le plateau initial soit toujours de hauteur $2\cdot \frac{1}{2}=1$ mais de largeur 2 au lieu de 1. On a alors $$ \int_{-\infty}^{+\infty}2\cos \pi x \;\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\;\mathrm{sinc}\frac{x}5\;\cdots\;\mathrm{sinc}\frac{x}{2N+1} \,\mathrm{d} x=1 $$ tant que $$ 2-\frac{1}{3}-\frac{1}{5}-\cdots-\frac{1}{2N+1} >0 $$ c'est-à-dire jusqu'à $2N+1=111$ (le 56^e terme), puis le 57^e terme décroche : $$ \int_{-\infty}^{+\infty}2\cos \pi x \;\mathrm{sinc} x\;\mathrm{sinc}\frac{x}3\;\mathrm{sinc}\frac{x}5\;\cdots\;\mathrm{sinc}\frac{x}{113} \,\mathrm{d} x\lt 1 $$

    Une suite d'intégrales similaires qui reste constante aussi loin que l'on veut

    Il suffit de prendre une série lentement divergente, par exemple (suivant une suggestion de J. Baez) : $$ \frac{1}{101} + \frac{1}{201} + \frac{1}{301} + \cdots $$ On a alors $$ \int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}{101}\;\mathrm{sinc}\frac{x}{201}\;\cdots\;\mathrm{sinc}\frac{x}{100N+1} \,\mathrm{d} x=1 $$ pour tout $$ N\lt 15\,341\,178\,777\,673\,149\,429\,167\,740\,440\,969\,249\,338\,310\,889 $$ (soit environ $1,5\cdot10^{43}$)11.

    À partir de cette idée, on peut construire des séries harmoniques de plus en plus lentes à diverger, pour obtenir une suite d'intégrales similaires qui reste constante aussi loin que l'on veut.

    Une suite d'intégrales similaires qui reste toujours constante

    Il suffit cette fois de considérer une série convergente de somme inférieure ou égale à 1. Par exemple, la série convergente $$ \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots = 1 $$ montre que chaque somme partielle est $\lt 1$. Le plateau de hauteur $1$ à $t=0$ perdurera toujours dans un produit de convolution $\Pi_1\ast\Pi_{\frac{1}{2}} \ast \Pi_{\frac{1}{4}} \ast \cdots$ et donc $$\int_{-\infty}^{+\infty}\mathrm{sinc} x\;\mathrm{sinc}\frac{x}2\;\mathrm{sinc}\frac{x}4\;\mathrm{sinc}\frac{x}8\;\mathrm{sinc}\frac{x}{16}\;\mathrm{sinc}\frac{x}{32}\;\cdots\;\mathrm{sinc}\frac{x}{2^N} \,\mathrm{d} x=1 $$ toujours.

    Exercice

    Établir la formule générale $$ \int_{-\infty}^{+\infty}\mathrm{sinc} a_1x\;\mathrm{sinc}{a_2x}\;\mathrm{sinc}{a_3x}\;\cdots\;\mathrm{sinc}{a_Nx} \,\mathrm{d} x=\frac{1}{|a_1|} $$ tant que $$ |a_2|+|a_3|+\cdots+|a_N|\lt |a_1|. $$

    Bibliographie

    E. T. Whittaker, On the Functions which are represented by the Expansions of the Interpolation-Theory, Proceedings of the Royal Society of Edinburgh A 35, 1915, 181—194.

    J. M. Whittaker, Interpolatory function theory, Cambridge University Press. 1935, 107 p.

    J. McNamee, F. Stenger and E. L. Whitney, ``Whittaker's Cardinal Function in Retrospect'', Mathematics of Computation 25(113) 1971, 141—154.

    D. Borwein and J. M. Borwein, Some remarkable properties of sinc and related integrals, The Ramanujan Journal 5, 2001, 73—89.

    H. Schmid, Two curious integrals and a graphic proof, Elem. Math. 69, 2014, 11—17.

    R. Baillie, D. Borwein and J. M. Borwein, Surprising sinc sums and integrals, Amer. Math. Monthly 115, 2008, 888—901.

    J. Baez. Patterns that eventually fail, 2018, Azimuth. https ://johncarlosbaez.wordpress.com/2018/09/20/patterns-that-eventually-fail/.