Les matrices forment ce qu'on appelle une algèbre : si on prend deux matrices, on peut les additionner et les multiplier. Ces deux opérations sont suffisantes pour définir un polynôme d'une matrice. Mais peut-on mieux faire ? Étant données une fonction $f$ et une matrice $M$, peut-on donner un sens à $f(M)$ ?
Les fonctions de matrices permettent de répondre à des questions a priori éloignées des problèmes d'algèbre linéaire, par exemple en équations différentielles. Regardons le système différentiel linéaire
$$\left \{
\begin{array}{rcl}
x'_1(t)&=& a_{1,1} x_1(t) + a_{1,2} x_2(t) + \ldots + a_{1,n} x_n(t) \\
x'_2(t)&=& a_{2,1} x_1(t) + a_{2,2} x_2(t) + \ldots + a_{2,n} x_n(t) \\
\vdots&&\\
x'_n(t)&=& a_{n,1} x_1(t) + a_{n,2} x_2(t) + \ldots + a_{n,n} x_n(t),\\
\end{array}
\right.$$ avec conditions initiales $(x_1(0), \ldots, x_n(0)) = (x_1^0, \ldots, x_n^0)$.
En définissant la matrice $A = (a_{i,j})_{(i,j) \in \{ 1, ..., n \}^2}$, et les vecteurs
$$X(t) = \begin{pmatrix} x_1(t) \\ x_2(t) \\ \vdots \\ x_n(t) \end{pmatrix} \text{ et } X_0 = \begin{pmatrix} x_1^0 \\ x_2^0 \\ \vdots \\ x_n^0 \end{pmatrix},$$ le problème se réécrit
$$\left \{
\begin{array}{ccc}
X'(t) &=& A X(t) \\
X(0) &=& X_0 \in \mathbb{R}^n.
\end{array}
\right.$$
Il a pour solution $X(t) = e^{tA} X_0$, où pour toute matrice M, on définit son exponentielle $e^{M}$ comme dans le cas scalaire par la série entière
$$ e^M = \exp(M) = \sum_{n=0}^\infty \frac{M^n}{n!}.$$ On montre par division euclidienne que cette matrice $\exp(M)$ est un polynôme en $M$ : il existe un polynôme $P$ tel que $P(M) = \exp(M)$. Attention, ce polynôme dépend de la matrice $M$, et ainsi la fonction matricielle exponentielle n'est pas une fonction polynomiale1. Pour résoudre un problème mathématique concret, on a donc été amené à considérer une première famille de fonctions matricielles non polynomiales, les exponentielles des matrices $tA$2.
Ces remarques nous amènent à nous poser la question suivante : quelles fonctions, a priori réelles ou complexes, peuvent être prolongées en fonctions matricielles ? Le problème est en fait mieux posé dans le sens inverse : étant donnée une matrice $M$, pour quelles fonctions réelles ou complexes la notation $f(M)$ a-t-elle un sens ? En toute généralité, $\exp(M)$ est un polynôme en $M$. En sera-t-il de même pour des fonctions plus générales de $M$ ?
Un cas bien connu : les polynômes de matrices
L'ensemble des matrices carrées de taille $n$ à coefficients complexes, noté $M_n(\mathbb{C})$, est une algèbre : si on prend deux matrices $A$ et $B$, on peut les additionner et les multiplier pour obtenir les matrices $A+B$ et $AB$. Cette algèbre possède une unité $I_n$, l'unique matrice telle que pour toute matrice $M$ on a $M I_n = I_n M = M$. Avec la convention $M^0 = I_n$, on peut définir la puissance de matrice $M^n$ pour tout $n \in \mathbb{N}$ et pour tout matrice $M \in M_n(\mathbb{C})$. Ensuite, étant donné un polynôme $P = \sum_{i=0}^d p_i X^i$, on peut évaluer le polynôme $P$ en la matrice $M$. C'est une matrice notée $P(M)$ donnée par la formule :
$$P(M) = \sum_{i=0}^d p_i M^i.$$
Attention, l'algèbre des matrices n'est pas commutative : on n'a pas forcément $AB= BA$. Il n'y a cependant pas de problème à définir les puissances de $A$ car l'algèbre des matrices est associative.
Les polynômes en une matrice forment une algèbre et $P \mapsto P(M)$ est un morphisme, c'est à dire que pour tout polynômes $P$ et $Q$,
- $(P+Q)(M) = P(M) + Q(M)$,
- $(PQ)(M) = P(M)Q(M)$,
- $1(M) = I_n$,
- $X(M) = M$,
- $(P \circ Q)(M)= P(Q(M))$.
- $P(R^{-1} M R) = R^{-1} P(M) R$, pour toute matrice inversible $R$.
Les polynômes de matrices sont des outils déjà très utiles et permettent de traiter de nombreuses questions en lien avec la réduction des endomorphismes. Par exemple, on sait qu'une matrice est diagonalisable si et seulement si elle admet un polynôme annulateur scindé à racines simples.
Nous souhaitons désormais définir $f(M)$ pour une classe de fonctions plus grande que les polynômes. L'association $f \mapsto f(M)$ sera appelée calcul fonctionnel pour $M$ et on attend qu'elle satisfasse les mêmes propriétés de morphisme1.
Le cas des matrices diagonalisables
Fonctions d'une matrice diagonalisable
Il existe une façon naturelle de définir $f(M)$ si $M$ est une matrice diagonalisable. Soit $M$ une telle matrice, il existe une matrice inversible $R$ telle que $M =R D R^{-1}$, où $D$ est une matrice diagonale de coefficients $\lambda_i$. On la notera aussi $D = diag(\lambda_i)$. Si $f$ est une fonction dont l'ensemble de définition contient le spectre (autrement dit, l'ensemble des valeurs propres) de $M$, définissons d'abord la matrice diagonale $f(D)$ par $f(D) = diag(f(\lambda_i))$, on définit ensuite $f(M)$ par $f(M) = R f(D) R^{-1} $. Cette définition coïncide bien avec la première définition dans le cas où $f$ est une fonction polynomiale car pour tout polynôme $P$, on montre que $P(R D R^{-1} ) = R P(D) R^{-1} $. Il est aussi facile de vérifier que les propriétés de morphismes de la partie précédente sont bien vérifiées par l'association $f \mapsto f(M)$. On peut tout de même se poser la question suivante : $f(M)$ est-elle indépendante des choix de $R$ et $D$ ? Nous donnerons une réponse positive à cette question dans la suite de l'article.
Une application : le problème de la racine carrée
Cette première approche nous permet de résoudre quelques problèmes bien connus des étudiants en mathématiques. Étudions celui de la racine carrée. Soit $S$ une matrice symétrique réelle définie positive (en particulier, ses valeurs propres sont toutes strictement positives), montrons qu'il existe une autre matrice symétrique réelle définie positive $S'$ telle que $(S')^2 = S$. Cette matrice est unique, et cela peut se montrer en étudiant les espaces propres de la matrice, ce que nous ne ferons pas dans cet article.
Comme une matrice symétrique réelle est diagonalisable, il suffit d'appliquer la construction précédente avec $f : x \mapsto \sqrt{x}$. On obtient $S' = R diag(\sqrt{\lambda_i}) R^{-1} $ qui est bien symétrique réelle. On a de plus
\begin{align*} (S')^2 &= R \,diag(\sqrt{\lambda_i}) \, R^{-1} \,R \, diag(\sqrt{\lambda_i}) \,R^{-1} \\&= R \,diag(\sqrt{\lambda_i}) diag(\sqrt{\lambda_i}) \, R^{-1} \\&= R \,diag(\lambda_i) \,R^{-1} = S. \end{align*}
Cette construction de la racine carrée fonctionne, au delà des matrices symétriques, pour toute matrice diagonalisable dont toutes les valeurs propres sont strictement positives.
Construction du calcul fonctionnel matriciel
Si la matrice n'est pas diagonalisable, on s'inspire tout de même du cas précédent en essayant d'utiliser les polynômes. Notons $P_M(X) = (-1)^n (X-\lambda_1)^{m_i} ... (X - \lambda_j)^{m_j}$ le polynôme caractéristique de $M$. Les $\lambda_i$ sont les valeurs propres distinctes de la matrice dans (dans $\mathbb{C}$) et les $m_j$ sont leurs multiplicités (algébriques) respectives.
Les polynômes interpolateurs de Lagrange
Soient $a_1, ..., a_j$ des nombres complexes deux à deux distincts et $f$ une fonction continue sur des voisinages des $a_i$. On peut trouver un unique polynôme de degré au plus $j-1$ tel que quelque soit $i$, $P(a_i) = f(a_i)$. On l'appelle de polynôme interpolateur de Lagrange de $f$ aux points $a_i$. On peut en donner une expression explicite : $$P(X) = \sum_{i=1}^j f(a_i) \prod_{k \ne i} \frac{X-a_k}{a_i-a_k}.$$
Bien qu'on puisse en donner une construction explicite, c'est en fait un résultat de dualité : les valuations en les $a_i$1 forment une base des formes linéaires sur $\mathbb{C}_{j-1}[X]$ ce qui donne directement l'existence et l'unicité d'un tel polynôme. On est dans le cadre typique d'un système d'équations qui possède autant d'inconnus que d'équations (indépendantes).
Prenons à nouveau $a_1, ..., a_j$ des nombres complexes deux à deux distincts. On leur associe $m_1, ..., m_j$ des entiers naturels. Soit $f$ une fonction suffisamment régulière2, on dit qu'un polynôme $P$ interpole $f$ aux points $(a_i)$ aux ordres $(m_i)$ si
$$\forall i \in \{1, ..., j\}, \forall k \in \{0,..., m_j - 1\}, P^{(k)}(a_i) = f^{(k)}(a_i).$$
Si on impose que le degré de $P$ soit strictement inférieur à $n= \sum_{i=1}^j m_i$, on obtient l'existence et unicité d'un tel polynôme par des résultats de dualité analogues au cas précédent3. Ce qui nous intéresse avant tout ici est l'existence d'un tel polynôme.
Le calcul fonctionnel matriciel
Nous avons maintenant en notre possession tous les outils nécessaires à la construction d'un calcul fonctionnel matriciel. Soit $M$ une matrice carrée à coefficients complexes, on souhaite définir $f(M)$ pour $f$ une fonction complexe définie sur un $\mathcal{U}$ un ouvert de $\mathbb{C}$ contenant les valeurs propres de $M$. Les propriétés de régularité qui nous intéressent ici sont à prendre au sens complexe, ainsi on dit qu'une fonction $f$ est $\mathbb{C}$-dérivable4 en $z_0$ si la quantité $\lim_{z \rightarrow z_0} \frac{f(z) - f(z_0)}{z-z_0}$ existe. Considérons $P$ un polynôme qui interpole $f$ aux points $\lambda_i$ et aux ordres $m_i$. On définit alors $f(M)$ par $P(M)$. Il faut vérifier que c'est une application bien définie, autrement dit qu'elle ne dépend pas du choix du polynôme d'interpolation $P$.
Théorème
(Calcul fonctionnel matriciel)La matrice obtenue par la construction précédente ne dépend pas du choix du polynôme interpolateur $P$. En d'autres termes, le calcul fonctionnel matriciel est bien défini.
Démonstration. Supposons $P$ et $Q$ deux polynômes qui interpolent $f$ aux points et ordres voulus. On a
$$\forall i \in \{1, ... , j\}, \forall k \in \{0,..., m_i - 1\}, P^{(k)}(\lambda_i) = f^{(k)}(\lambda_i) = Q^{(k)}(\lambda_i). $$
Ainsi le polynôme $P - Q$ admet les complexes $\lambda_i$ comme racines d'ordre au moins $m_i$. Donc pour tout $i \in \{1, ... , j\}$, le polynôme $(X-\lambda_i)^{m_i}$ divise $P-Q$. Comme ces derniers polynômes sont deux à deux premiers entre eux, $\prod_{i=1}^j (X-\lambda_i)^{m_i} $ divise $P-Q$. Il existe donc un polynôme $D$ tel que $$P-Q = \prod_{i=1}^j (X-\lambda_i)^{m_i} D = (-1)^n P_M D. $$
Autrement dit, $P_M$ divise $P-Q$. En évaluant cette dernière égalité en $M$, on obtient $P(M) = Q(M)$ par le Théorème de Cayley-Hamilton1, ce qui termine la démonstration.
En fait, on aurait pu se contenter d'interpoler $f$ aux ordres de multiplicité géométriques (c'est à dire l'ordre des valeurs propres dans le polynôme minimal) pour avoir ce résultat. C'est le théorème suivant.
Théorème
Soit $M \in M_n(\mathbb{C})$ et $P, Q \in \mathbb{C}[X]$. Soit $\mu_M(X) = \prod_{i=1}^j (X-\lambda_i)^{\omega_i}$ le polynôme mininal de $M$. Les propositions suivantes sont équivalentes.
- $P(M) = Q(M)$,
- $\forall i \in \{1, ...,j\}, \forall k \in \{0,..., \omega_i - 1\}, P^{(k)}(\lambda_i) = Q^{(k)}(\lambda_i)$,
- $\mu_M$ divise $P-Q$.
Le calcul fonctionnel est donc bien défini indépendamment du choix du polynôme interpolateur. Ceci répond en particulier à la question laissée en suspens : le calcul fonctionnel défini pour les matrices diagonalisables ne dépendait pas du choix de la matrice de passage.
Ce calcul fonctionnel hérite automatiquement des propriétés de morphismes du calcul fonctionnel polynomial : pour toutes fonctions $f$ et $g$ de classe $C^\infty$ sur un ouvert $\mathcal{U}$ contenant les valeurs propres de $M$,
- $(f+g)(M) = f(M) + g(M)$,
- $(fg)(M) = f(M)g(M)$,
- $\chi(M) = I_n$, où $\chi$ est la fonction constante égale à 1,
- $id(M) = M$, où $id$ est la fonction identité1 sur $\mathbb{C}$,
- $f \circ g(M) = f (g (M))$,
- $f(R^{-1} M R) = R^{-1} f(M) R$, pour toute matrice inversible $R$.
Cela se prouve en vérifiant que si $P$ et $Q$ interpolent respectivement $f$ et $g$ aux points et aux ordres souhaités, alors $P + Q$ y interpole $f + g$, $PQ$ y interpole $fg$ et ainsi de suite. On peut par ailleurs montrer que ce calcul fonctionnel est unique au sens où il est l'unique application de $C^\infty(\mathcal{U})$ dans $M_n(\mathbb{C})$ vérifiant les propriétés $1$ à $4$.
Ce calcul est bien évidement consistant avec le calcul polynomial. On peut vérifier qu'il aussi compatible avec avec une autre familles de fonctions de matrices beaucoup utilisés en algèbre linéaire : les résolvantes. En effet, si on prend $f(z) = (z-\mu)^{-1}$ pour $\mu$ en dehors du spectre de $M$, on retrouve bien $f(M) = (M-\mu I_n)^{-1}$.
Enfin, les propriétés de morphismes assurent que de nombreuses relations fonctionnelles sur les scalaires on pourra déduire une relation fonctionnelle sur les matrices. Par exemple, pour toute matrice $M \in M_n(\mathbb{C})$ on aura $\sin(M)^2 + \cos(M)^2 = I_n$. Les développements limités ou en séries entières usuels seront aussi vrais pour les fonctions matricielles.
La formule de Sylvester et l'approche numérique
Les propriétés du calcul fonctionnel et l'expression du polynôme d'interpolation de Lagrange permettent d'établir la formule suivante, appelée formule de Sylvester. Pour toute matrice $M$ diagonalisable de valeurs propres $\{ \lambda_1, ... , \lambda_k \}$ et toute fonction définie sur un voisinage de ces valeurs propres
$$ f(M) = \sum_{i=1}^k f(\lambda_i) \prod_{j \ne i} \frac{A - \lambda_j I_n}{\lambda_i - \lambda_j}.$$
Notons qu'il existe des formules analogues dans le cas non diagonalisable. Cette formule donne une première approche au calcul numérique de ces fonctions de matrices. C'est un problème difficile mais possible : la formule effective réduit le problème au calcul des valeurs propres de la matrice en question. Pour approcher numériquement les valeurs propres d'une matrice, on peut utiliser la méthode QR2. Le problème de cette méthode est qu'elle nécessite notamment que la matrice possède $n$ valeurs propres de modules différents, ce qui est faux sur un certain nombre d'exemples concrets.
Un exemple sur des matrices non-diagonalisables
Nous concluons cette partie en traitant de façon complètement explicite le calcul fonctionnel de certaines matrices : les blocs de Jordan nilpotents. Commençons par la dimension 2. On définit la matrice de Jordan nilpotente en dimension 2 par
$$J_2 = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}.$$
Elle possède une unique valeur propre double, $0$, et n'est pas diagonalisable. Son polynôme caractéristique est $X^2$. Si $f$ est une fonction dérivable (au sens complexe) autour de zéro on cherche un polynôme $P$ vérifiant $P(0) = f(0)$ et $P'(0)=f'(0)$. En résolvant le système obtenu, on obtient $P(X) = f(0) + f'(0) X$. Le calcul fonctionnel de $M$ est alors donné par $f(M) = f(0) I_2 + f'(0) J_2 $, soit
$$f(M) = \begin{pmatrix} f(0) &f'(0) \\ 0& f(0) \end{pmatrix}. $$
Et en dimension $n$ ? On regarde toujours la matrice de Jordan
$$J_n = \begin{pmatrix} 0 & 1 & 0 & \ldots & 0\\
0 & 0 & 1 & \ldots & 0\\
\vdots& \vdots & 0& \ddots & \vdots\\
0 & 0 & 0 & \ddots & 1\\
0 & 0 & 0 & \ldots & 0 \end{pmatrix}.$$
Son polynôme caractéristique est $(-X)^n$. Pour déterminer $f(M)$, on cherche un polynôme $P$ de degré $n-1$ tel que pour tout $k \in \{0, ... , n-1\}, P^{(k)}(0) = f^{(k)}(0)$. On trouve $P(X) = \sum_{k=0}^{n-1} \frac{ f^{(k)}(0)}{k!} X^k$. Ainsi le calcul fonctionnel de $J_n$ est donné par
$$f(J_n) = \sum_{k=0}^{n-1} \frac{ f^{(k)}(0)}{k!} J_n^k
= \begin{pmatrix} f(0) & f'(0) & \frac{f''(0)}{2}& \ldots & \frac{f^{(n-1)}(0)}{(n-1)!}\\
0&f(0) & f'(0) & \ldots & \frac{f^{(n-2)}(0)}{(n-2)!}\\
\vdots& \vdots & f(0)& \ddots & \vdots\\
0 & 0 & 0 & \ddots & f'(0)\\
0 & 0 & 0 & \ldots & f(0) \end{pmatrix}.$$
C'est un cas particulier de bloc de Jordan. En général, pour $\lambda \in \mathbb{C}$, pour la matrice
$$J_n(\lambda) = \begin{pmatrix} \lambda & 1 & 0 & \ldots & 0\\
0 & \lambda & 1 & \ldots & 0\\
\vdots& \vdots & \lambda& \ddots & \vdots\\
0 & 0 & 0 & \ddots & 1\\
0 & 0 & 0 & \ldots & \lambda \end{pmatrix},$$
on obtient $f(J_n(\lambda)) = P(J_n(\lambda))$ avec $P(X) = \sum_{k=0}^{n-1} \frac{(X-\lambda)^k}{k!}$. Ainsi pour toute fonction $f$ suffisament dérivable sur un voisinage de $\lambda$,
$$ f(J_n(\lambda)) = \sum_{k=0}^{n-1} \frac{ f^{(k)}(\lambda)}{k!} J_n^k
= \begin{pmatrix} f(\lambda) & f'(\lambda) & \frac{f''(\lambda)}{2}& \ldots & \frac{f^{(n-1)}(\lambda)}{(n-1)!}\\
0&f(\lambda) & f'(\lambda) & \ldots & \frac{f^{(n-2)}(\lambda)}{(n-2)!}\\
\vdots& \vdots & f(\lambda)& \ddots & \vdots\\
0 & 0 & 0 & \ddots & f'(\lambda)\\
0 & 0 & 0 & \ldots & f(\lambda) \end{pmatrix}.$$
Un exemple en grande dimension
Nous vous proposons de vous exercer à expliciter le calcul fonctionnel sur la matrice
$$ B = \begin{pmatrix} 1 & 1 & 1 & 1\\
1 & 1 & 1 & 1\\
1 & 1 & 1 & 1\\
1 & 1 & 1 & 1
\end{pmatrix}. $$
Vous pourrez aussi vous intéresser à la matrice $B_n \in M_n(\mathbb{R})$ dont tous les coefficients sont égaux à 1.
La matrice $B$ est de rang $1$, donc son noyau est de dimension $3$. Le vecteur constant égal à $1$ est vecteur propre associé à la valeur propre $4$. Ainsi, $B$ est diagonalisable et son polynôme minimal est $X (X-4)$. Pour déterminer $f(B)$, il suffit de trouver un polynôme $P = aX + b$ de degré $1$ tel que $P(0) = f(0)$ et $P(4) = f(4)$. Ceci donne $b = f(0)$ et $f(4) = 4 a + b$, donc $a = \frac{f(4) - f(0)}{4}$. Pour toute fonction $f$ de classe $C^\infty$ sur un voisinage de $0$ et $4$ on a donc
\begin{equation*}f(B) = \frac{f(4)-f(0)}{4} B + f(0) I_4. \end{equation*} Ainsi, $$f(B) = \frac{1}{4} \begin{pmatrix} f(4) + 3 f(0) & f(4)-f(0) & f(4)-f(0) & f(4)-f(0)\\ f(4)-f(0)& f(4) + 3 f(0) & f(4)-f(0)& f(4)-f(0)\\f(4)-f(0) &f(4)-f(0) & f(4) + 3 f(0) &f(4)-f(0) \\ f(4)-f(0)&f(4)-f(0) & f(4)-f(0)& f(4) + 3 f(0) \end{pmatrix}.$$
De même, la matrice $B_n$ a un noyau de dimension $n-1$ et le vecteur constant égal à $1$ est vecteur propre pour la valeur propre $n$. Le polynôme minimal de $B_n$ est alors $X(X-n)$ et on obtient le calcul fonctionnel
$$f(B_n) = \frac{f(n) - f(0)}{n}B_n + f(0) I_n. $$
Quelques applications
Dans cette partie, nous donnons quelques applications de l'existence d'un tel calcul et de sa construction.
Le calcul de l'exponentielle matricielle
L'exponentielle matricielle, formellement définie par $\exp(M) = \sum_{n=0}^\infty \frac{M^n}{n!}$, est souvent fastidieuse à calculer : la formule explicite est rarement utilisable en pratique. S'il est possible d'utiliser une diagonalisation (ou une forme de Jordan) pour calculer une exponentielle, ces calculs sont coûteux et peuvent occasionner de nombreuses erreurs.
La construction du calcul fonctionnel matriciel nous donne une façon très pratique de calculer l'exponentielle de $M$. La dimension finie de l'espace des matrices nous assure que $\exp(M)$ est un polynôme en $M$ mais sans nous donner explicitement ce polynôme. C'est ce polynôme que la construction du calcul fonctionnel nous permet d'obtenir : il suffit de prendre le polynôme qui interpole l'exponentielle aux points et degrés voulus. Il suffit ici de résoudre un unique système linéaire.
Prenons l'exemple de la matrice du quart de tour. Elle est définie par
$$R_{\frac{\pi}{2}} = \begin{pmatrix}
0 & -1 \\ 1 &0
\end{pmatrix}.$$
Son polynôme caractéristique est $X^2 +1$. Ainsi ses valeurs propres sont $i$ et $-i$. Ce sont des valeurs propres simples. Pour une fonction donnée $f$, un polynôme $P(X) = a X + b$ vérifiera $P(M) =f(M)$ si et seulement si $P(i) = f(i)$ et $P(-i) = f(-i)$. On trouve $P$ en résolvant le système :
$$\left \{
\begin{array}{rc}
a i + b&=& f(i) \\
-a i + b &=& f(-i).
\end{array}
\right.$$
La résolution du système donne $a = \frac{f(i) - f(-i)}{2i}$ et $b = \frac{f(i) + f(-i)}{2}$. Avec $f(z) = e^{tz}$ on obtient $a = \sin(t)$ et $b=\cos(t)$, soit
$$e^{t R_{\frac{\pi}{2}}} = \sin(t) R_{\frac{\pi}{2}} + \cos(t) I_2 = \begin{pmatrix} \cos(t) & -\sin(t) \\ \sin(t) & \cos(t)\end{pmatrix}. $$
La méthode permet même d'obtenir des formules générales pour certains cas. Ainsi pour une matrice carrée $A$ de taille $n$ possédant une unique valeur propre $\lambda$, on peut montrer que $\exp(A) = e^{t\lambda} [I_n + t (A-\lambda I_2) + ... + \frac{t^{n-1}}{(n-1)!}(A- \lambda I_2)^{n-1}]$.
L'équation des ondes
Avec ces méthodes, on peut traiter certaines équations différentielles linéaires d'ordre supérieur. Soit $A$ une matrice dont toutes les valeurs propres sont strictement positives, on regarde l'équation
$$\left \{
\begin{array}{rcl}
X''(t) + A X(t) = 0 \\
X(t) = X_0 \in \mathbb{R}^n \\
X'(t) = V_0 \in \mathbb{R}^n.
\end{array}
\right.$$
La solution du problème est donnée par
$$X(t) = \cos(t \sqrt{A}) X_0 + \sqrt{A}^{-1} \sin(t \sqrt{A}) V_0. $$
Un exemple d'équation de ce type est l'équation des ondes discrète en espace (en dimension $1$). Le choix de la matrice $$A = \begin{pmatrix} 2 & -1 & 0& \dots & 0 \\ -1 & 2 & - 1 & \ddots & 0 \\ 0 & \ddots & \ddots & \ddots & \vdots\\ \vdots & \ddots & -1 & 2 &- 1 \\ 0& \dots & 0 & -1 & 2\end{pmatrix}$$ correspond à cet exemple.
L'écriture de la solution de ce problème à l'aide calcul fonctionnel matriciel permet d'apprendre une surprenante propriété de ses solutions : les solutions de l'équation des ondes discrètes1 ont une vitesse de propagation infinie. Considérons le problème avec pour données initiales $X_0$ à coefficients positifs ou nuls et $V_0 = (0, \dots, 0 )$, alors dès que $t$ est strictement positif, l'onde s'est déjà propagée sur tous les points de la discrétisation. En effet, la solution du problème est
\begin{align*}X(t) &= \cos(t \sqrt{A}) X_0 \\ &= \sum_{n=0}^{+\infty} \frac{(t\sqrt{A})^{2n}}{(2n)!} X_0\\ &= \sum_{n=0}^{+\infty} \frac{t^{2n}A^{n}}{(2n)!} X_0. \end{align*} Comme la matrice $A$ est tridiagonale, $A^n_{i,j}$ est non nul si et seulement si $n \ge |i-j| $. Ainsi, lorsque $t$ est proche de $0$, $[\cos(t \sqrt{A})X_0]_i$ se comporte comme $t^{2 D(i,S(X_0))}$, où $D(i,S(X_0))$ est la distance entre $i$ et $S(X_0) = \{ i \in \{1, \dots, n\}, [X_0]_i \ne 0 \}$ le support de $X_0$. L'onde est donc propagée sur tous les points dès que $t>0$.2
Remarquons que cet exemple est plus facile à traiter numériquement. La racine carrée d'une matrice symétrique définie positive se calcule bien de façon itérative avec l'algorithme de Héron.3 Le calcul de la série peut ensuite se faire par troncature de la série, dont il est facile d'estimer l'erreur. La méthode QR évoquée précédemment peut aussi être utilisée car les valeurs propres de $A$ sont toutes de module différent4. Ainsi une fois les valeurs propres de $A$ approchées, il ne restera plus qu'à calculer de polynôme d'interpolation qui réalise le calcul fonctionnel ou utiliser directement la formule de Sylvester.
Le logarithme matriciel
On s'intéresse au problème suivant : soit $M \in M_n(\mathbb{C})$, à quelle condition existe-t-il une matrice $N$ telle que $$\exp(N) = M ?$$
La matrice $N$ est alors en quelque sorte le "logarithme" de la matrice $N$. La formule $\exp(N) \exp(-N) = \exp(0_n) = I_n$ nous indique que toutes les matrices pour lesquelles la réponse est positive doivent être inversibles. C'est en fait une condition nécessaire et suffisante. Le calcul fonctionnel matriciel nous permet d'exhiber une matrice qui résoudra le problème.
Pour comprendre ce qu'il se passe, regardons d'abord le cas des matrices dont toutes les valeurs propres sont strictement positives. Le calcul fonctionnel permet de définir la matrice $N = \ln(M)$. Dès lors, la compatibilité du calcul fonctionnel matriciel avec la composition donne
\begin{align*} \exp(N) &= \exp(\ln(M)) \\ &= (\exp \circ \ln ) (M)\\&= Id(M) \\&= M.\end{align*}
Le cas général se traite de la même manière. Soit $M \in M_n(\mathbb{C})$ une matrice inversible. Le complémentaire, dans $\mathbb{C}$, du spectre de M est un ouvert très simple : il s'agit du plan privé d'un nombre fini de point. Comme la matrice est inversible, $0$ appartient à cet ensemble. On peut donc tracer une demi-droite qui part de zéro vers l'infini, dans une certaine direction, tout en évitant le spectre de $M$. Soit $\mathcal{U}$ le plan complexe privé de cette demi-droite. Il existe ce qu'on appelle une détermination du logarithme sur $\mathcal{U}$ : c'est à dire qu'il existe une fonction dérivable1 telle que pour tout $z \in \mathcal{U}$, $\exp(f(z)) = z$. Posons $N = f(M)$. On a alors
\begin{align*} \exp(N) &= \exp(f(M)) \\ &= (\exp \circ f ) (M)\\&= Id(M) \\&= M.\end{align*}
Ceci nous prouve que $M$ est bien dans l'image de l'exponentielle matricielle. Ainsi nous avons démontré le résultat suivant.
Théorème
(Image de l'exponentielle matricielle)Soit $M \in M_n(\mathbb{C})$. Il existe $N \in M_n(\mathbb{C})$ telle que $\exp(N) = M$ si et seulement si $M$ est inversible.
Les racines et la valeur absolue
Nous avons vu comment définir une racine carrée pour une matrice réelle symétrique définie positive. On peut faire de même pour certaines matrices à coefficients complexes. La façon la plus simple de définir une fonction racine carrée sur les nombres complexes est $\sqrt{\rho e^{i \theta}} = \sqrt{\rho} e^{i \frac{\theta}{2}}$ si $\rho \in [0, + \infty[$ et $\theta \in ]-\pi,\pi]$. Attention, cette fonction n'est pas continue sur le demi-axe réel négatif, on préfèrera la définir sur $\mathbb{C}\backslash \mathbb{R}_-$. Cette racine carrée vérifie $\forall z \in \mathbb{C} \backslash \mathbb{R}_-, \sqrt{z}^2 = z$. Le calcul fonctionnel nous permet alors de définir $\sqrt{M}$ pour une matrice $M \in M_n(\mathbb{C})$ qui n'a pas de valeur propre négative ou nulle. La compatiblité avec la composition donne $\sqrt{M}^2 = M$. Ainsi toute matrice qui ne possède pas de valeur propre négative ou nulle admet une racine carrée. De même, en définissant une racine $n$-ième complexe par $(\rho e^{i \theta})^{1/n} = \rho^{1/n} e^{i \theta/n}$ si $\rho \in [0, + \infty[$ et $\theta \in ]-\pi,\pi[$, on construit une racine $n$-ième pour ces matrices. On peut aller un peu plus loin avec le résultat suivant.
Théorème
Soit $M \in M_n(\mathbb{C})$ une matrice inversible et $n \ge 2$ un entier. Il existe $B \in M_n(\mathbb{C})$ tel que $B^n = M$.
Démonstration. On a précédement vu qu'il existe une matrice $N \in M_n(\mathbb{C})$ telle que $\exp(N) = M$. Posons $B = \exp\left( \frac{\ln(M)}{n}\right)$ et vérifions qu'elle répond au problème posé. \begin{align*} B^n &= \exp\left( \frac{\ln(M)}{n}\right)^n \\ &= \exp(\ln(M)) \\ &= M. \end{align*}
La racine carrée permet de définir la valeur absolue complexe. C'est la fonction définie par $V(z) = \sqrt{z^2}$ qui est une fonction dérivable sur $\mathbb{C} \backslash i \mathbb{R}$. Attention, elle est bien différente du module qui n'est pas une fonction dérivable ! Un calcul simple permet de voir pour tout complexe $z$ de partie réelle strictement positive, $V(z) = z$, et $V(z) = -z$ si $Re(z) < 0$. La fonction matricielle analogue définie par calcul fonctionnel aura un comportement similaire. Si $A$ est une matrice sans valeur propre dans la droite imaginaire, alors elle admet une décomposition $A = A_+ - A_-$ où $A_+$ (respectivement $A_-$) est la restriction de la matrice aux espaces caractéristiques associés aux valeurs propres de partie réelle positve (respectivement négative). On aura alors $V(A) = A_+ + A_-$.
Une application de l'holomorphie : la formule de Dunford
Cette partie, plus difficile, pourra être vue en seconde lecture. Elle requiert notamment des notions en analyse complexe à une variable.
La formule de Dunford et la continuité du calcul fonctionnel
Dans cet article, on a défini $f(M)$ pour des fonctions $f$ suffisamment $\mathbb{C}$-dérivables au voisinage des valeurs propres de la matrice $M$. Une fonction $\mathbb{C}$-dérivable est en fait appelée holomorphe. Cette condition est en fait très forte et une telle fonction a de nombreuses propriétés : elle est par exemple automatiquement $C^\infty$ et même analytique.
Le résultat suivant, appelé formule de Dunford, est une justification de ce choix. Il donne une autre construction du calcul fonctionnel matriciel, qui peut être adaptée pour définir une calcul fonctionnel pour un opérateur, borné ou pas, sur un espace de Banach.
Théorème
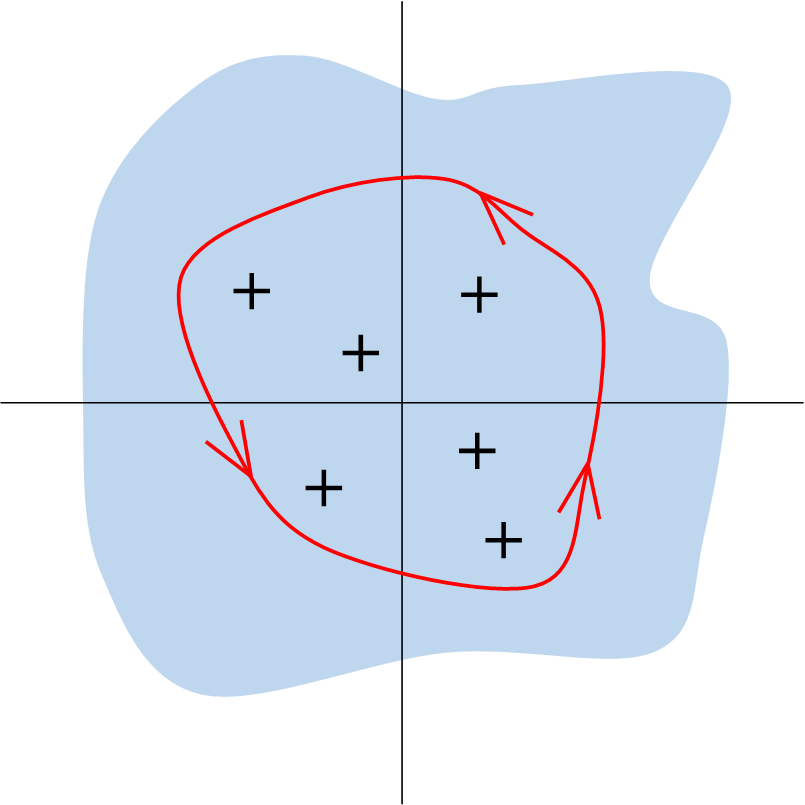
(Formule de Dunford)Soit $M \in M_n(\mathbb{C})$ et $f$ une fonction holomorphe sur un ouvert $\mathcal{U}$ contenant l'ensemble des valeurs propres de $M$. Alors pour tout chemin $\Gamma$1 orienté positivement autour du spectre de $M$,
$$f(M) = \frac{1}{2 i \pi} \int_\Gamma f(z) (z I_n - M)^{-1} dz.$$
Le contour $\Gamma$ est représenté en rouge autour des valeurs propres de $M$ (les croix noires). Le contour est inclus dans l'ouvert $\mathcal{U} \subset \mathbb{C}$ représenté en bleu.
Commençons par quelques remarques sur cette formule. Elle nous apporte une information qui était moins visible à partir de la construction du calcul fonctionnel à partir des polynômes d'interpolation : il est continu. En effet si on perturbe légèrement les coefficients de $M$, on perturbera aussi de façon légère ceux des résolvantes $(zI_n -M)^{-1}$, et par conséquent on ne modifiera que légèrement les coefficients de $f(M)$. De même, pour une matrice $M$ fixée, si la fonction $f$ est légèrement modifiée1, les coefficients de $f(M)$ seront eux aussi peu modifiés. D'un point de vue numérique, la méthode des trapèzes permet d'approcher l'intégrale de la formule. Cette méthode est efficace pour une discrétisation très précise, mais implique un grand nombre de coûteuses inversions de matrices.
Démonstration de la formule de Dunford. Par souci de simplicité, nous démontrons ce résultat pour les matrices $J_n(\lambda)$ que nous avons étudiées précédemment (rappelons que pour $\lambda = 0$, on note plus simplement $J_n(0) = J_n$). En fait, les propriétés du calcul fonctionnel ainsi que la réduction de Jordan suffisent à passer du cas de $J_n(\lambda)$ au cas général. Soit $f$ une fonction holomorphe sur un ouvert contenant l'unique valeur propre de $J_n(\lambda)$, autrement dit un voisinage de $\lambda$. Soit $\Gamma$ un contour autour de $\lambda$ inclus dans $\mathcal{U}$. En remarquant que pour tout $z \ne \lambda$, $$(z I_n-J_n(\lambda))^{-1} = ((z - \lambda) I_n -J_n)^{-1} = \sum_{k=0}^{n-1} (z-\lambda)^{-k-1} J_n^{k-1},$$ on obtient
\begin{align*}\frac{1}{2 i \pi} \int_\Gamma f(z) (z I_n - J_n(\lambda))^{-1} dz &= \frac{1}{2 i \pi} \sum_{k=0}^{n-1}\int_\Gamma f(z) (z-\lambda)^{-k-1} J_n^{k}dz \\
&= \sum_{k=0}^{n-1}\left( \frac{1}{2 i \pi} \int_\Gamma \frac{f(z)}{(z-\lambda)^{k+1}} dz\right) J_n^k \\ &= \sum_{k=0}^{n-1} \frac{f^{(k)}(\lambda)}{k!} J_n^k. \end{align*}
La dernière inégalité venant de la formule de Cauchy2, qui utilise l'holomorphie de la fonction : $$ \int_\Gamma \frac{f(z)}{(z-\lambda)^{k+1}} dz = \frac{f^{(k)}(\lambda)}{k!}.$$
On retrouve $$ \frac{1}{2 i \pi} \int_\Gamma f(z) (z I_n - J_n(\lambda))^{-1} dz = f(J_n(\lambda))$$ comme obtenu dans la troisième partie de cet article. Ceci conclut la démonstration dans le cas de la matrice $J_n(\lambda)$.
Il peut-être intéressant de démontrer les propriétés de morphisme du calcul fonctionnel à partir de cette construction, ou encore de comprendre pourquoi l'intégrale ne dépend pas du chemin $\Gamma$ choisi.
Sur un espace de Banach, pour un opérateur linéaire borné $T$, on construit un calcul fonctionnel de la même façon, en intégrant $f(z) (z Id - T)^{-1}$ sur un contour qui encercle le spectre de $T$. Si $T$ n'est pas borné, ce sera plus compliqué car on ne pourra pas encercler le spectre avec un contour fini : il faudra imaginer un autre chemin d'intégration, infini cette fois.
Quelques exercices
En guise d'exercices finaux, nous vous proposons de retrouver le calcul fonctionnel des matrices $R_{\frac{\pi}{2}}$ et $B$ à l'aide de la formule de Dunford. On pourra utiliser la formule des résidus qui est une généralisation de la formule de Cauchy. Celle-ci s'énonce simplement dans le cas des fonctions qui possèdent deux pôles simples : si $g$ est une fonction holomorphe sur $\mathcal{U}$ et $\Gamma$ est un contour orienté positivement autour de $a,b \in \mathcal{U}$,
$$ \frac{1}{2i \pi} \int_\Gamma \frac{g(z)}{(z-a)(z-b)} dz = \frac{g(a) - g(b)}{a-b}.$$
Ce n'est cependant pas une obligation d'utiliser cette formule et on pourra se ramener à une formule de Cauchy plus simple en utilisant une décomposition en éléments simples.
Regardons ce l'on obtient dans le cas de la matrice du quart de tour $R_{\frac{\pi}{2}}$. C'est une matrice carrée de taille $2$, donc on peut facilement calculer les matrices $(zI_2 - R_{\frac{\pi}{2}})^{-1}$ pour $z \in \mathbb{C} \backslash \{i,-i\}$. Pour une matrice $M$ de dimension $2$, le polynôme caractéristique est $$P_M(X) = X^2 - Tr(M) X + det(M) I_2.$$
Ainsi, $$P_{R_{\frac{\pi}{2}}}(X) = X^2 - Tr(z I_2 - R_{\frac{\pi}{2}}) X + det (z I_2- R_{\frac{\pi}{2}}) I_2.$$
Le théorème de Cayley-Hamilton assure alors que
$$(z I_2 - R_{\frac{\pi}{2}})^2 - Tr(z I_2 - R_{\frac{\pi}{2}}) (zI_2 - R_{\frac{\pi}{2}}) = - det (z I_2 - R_{\frac{\pi}{2}}) I_2.$$
Comme les valeurs propres de $R_{\frac{\pi}{2}}$ sont $i$ et $-i$, on obtient $Tr(zI_2 - R_{\frac{\pi}{2}}) = 2z$ et $det(zI_2-R_{\frac{\pi}{2}}) = (z-i)(z+i) = 1+z^2$.
On obtient
$$ (zI_2- R_{\frac{\pi}{2}}) (z I_2 - R_{\frac{\pi}{2}} - 2z I_2) = - (1+z^2) I_2.$$
Donc $$(z I_2 -R_{\frac{\pi}{2}})^{-1} = \frac{zI_2 + R_{\frac{\pi}{2}}}{1+z^2} = \frac{2z}{1+z^2} I_2 + \frac{1}{1+z^2} R_{\frac{\pi}{2}}.$$
Soit $f$ une fonction holomorphe sur un ouvert $\mathcal{U}$ contenant $i$ et $-i$. Soit $\Gamma \subset \mathcal{U}$ un contour orienté positivement autour de $i$ et $-i$ (par exemple si $\mathcal{U} = \mathbb{C}$ on peut prendre pour $\Gamma$ le cercle de centre $0$ et de rayon $2$). L'intégrale de la formule de Dunford donne
$$ \frac{1}{2 i \pi} \int_\Gamma f(z) (z I_2 - R_{\frac{\pi}{2}})^{-1} dz = \left( \frac{1}{2 i \pi} \int_\Gamma \frac{z f(z)}{1+z^2} dz \right) I_2 + \left( \frac{1}{2i\pi} \int_\Gamma \frac{f(z)}{1+z^2} dz \right) R_{\frac{\pi}{2}}. $$
Les deux intégrales en jeu se calculent par la formule des résidus. Par exemple, pour la première,
\begin{align*}\frac{1}{2 i \pi} \int_\Gamma \frac{z f(z)}{1+z^2} dz &= \frac{1}{2 i \pi} \int_\Gamma \frac{z f(z)}{(z-i)(z+i)} dz \\&= \frac{i f(i)}{2i} + \frac{if(-i)}{2i} = \frac{f(i) + f(-i)}{2}.
\end{align*}
Pour la deuxième, on a
\begin{align*}\frac{1}{2 i \pi} \int_\Gamma \frac{f(z)}{1+z^2} dz &= \frac{1}{2 i \pi} \int_\Gamma \frac{f(z)}{(z-i)(z+i)} dz \\&= \frac{ f(i)}{2i} + \frac{f(-i)}{-2i} = \frac{f(i) - f(-i)}{2i}.
\end{align*}
On a bien retrouvé la obtenue précédemment par interpolation de Lagrange
$$f(R_{\frac{\pi}{2}}) = \frac{f(i) - f(-i)}{2i} R_{\frac{\pi}{2}} + \frac{f(i) + f(-i)}{2} I_2.$$
Comme vu précédemment, la matrice $B$ admet $X(X-4)$ pour polynôme minimal. Ainsi $B (B- 4 I_4) =0$. Cette identité nous permet de calculer les résolvantes $(z I_4-B)^{-1}$ pour $z \in \mathbb{C} \backslash \{0,4\}$. En effet, cherchons un inverse à $z I_4 - B$ de la forme $a I_4 + c B$. Grâce à l'identité $B^2 = 4 B$, $(z I_4 - B)(aI_4 + c B) = I_4$ donne
$$ z aI_4 + (zc - a - 4 c) B = I_4. $$ On remarque que les choix $a = \frac{1}{z}$ et $ c =\frac{1}{z(z-4)} $ conviennent.
Soit $f$ une fonction holomorphe sur une voisinage $\mathcal{U}$ de $0$ et $4$ et $\Gamma \subset \mathcal{U}$ un contour orienté positivement autour de $0$ et $4$. La formule de Dunford donne $$ f(B) = \frac{1}{2i \pi} \int_\Gamma \frac{f(z)}{z} I_4 dz + \frac{1}{2i \pi} \int_\Gamma \frac{f(z)}{z(z-4)} B dz.$$
La première intégrale se calcule directement par formule de Cauchy et vaut $f(0)$. Pour la deuxième, on peut utiliser la formule des résidus. On peut aussi utiliser la décomposition en éléments simples $\frac{1}{z(z-4)} = \frac{1}{4(z-4)} - \frac{1}{4z}$ pour la calculer \begin{align*}
\frac{1}{2i \pi} \int_\Gamma \frac{f(z)}{z(z-4)} dz &= \frac{1}{2i \pi} \int_\Gamma \frac{f(z)}{4(z-4)} dz - \frac{1}{2i \pi} \int_\Gamma \frac{f(z)}{4z} dz \\&= \frac{f(4)}{4} - \frac{f(0)}{4}.
\end{align*} On retrouve bien le calcul fonctionnel donné par interpolation de Lagrange, soit
$$f(B) = f(0) I_4 + \frac{f(4) - f(0)}{4} B. $$
Quelques références.
Positive Operator Semigroups de András Bátkai, Marjeta Kramar Fijavž et Abdelaziz Rhandi. Le calcul fonctionnel matriciel est défini dans les premiers chapitres et de nombreuses applications sont données.
Matrices. Theory and Applications de Denis Serre. Pour d'autres applications du calcul fonctionnel matriciel et notamment de la formule de Dunford.
The Functional Calculus for Sectorial Operators de Markus Haase. Pour aller plus loin et découvrir le calcul fonctionnel pour un opérateur non borné, basé sur la formule de Dunford.