La géométrie a un rapport avec nos sensations et la bonne vieille géométrie d’Euclide n’est pas la seule possible, ni la seule utile...
Le but de cet article est d’abord d’illustrer, sans aucune technicité, sur l’exemple de la géométrie élémentaire, les notions de théorie axiomatique, de déduction formelle, d’interprétation, d’indécidabilité (on montrera, à propos du postulat des parallèles, comment on peut parfois prouver tout naturellement qu’une proposition est indécidable dans une théorie donnée). On verra aussi que la géométrie a un rapport avec nos sensations et que la bonne vieille géométrie d’Euclide n’est pas la seule possible, ni la seule utile. On évoquera un monde non euclidien imaginé par Poincaré, et on conclura par un mot sur notre monde physique.
La géométrie d’Euclide
Le livre 1 des Éléments de géométrie1 d’Euclide (vers l’an \(-300\)) commence par donner des « Définitions » des termes de la géométrie : « points », « lignes », « (lignes) droites », « angles », « cercles »,… En voici quelques-unes (il sera question ici presque uniquement de la géométrie plane) :
-
Le point est ce qui n’a aucune partie.
-
La ligne est une longueur sans largeur.
-
Les extrémités d’une ligne sont des points.
-
La ligne droite est celle qui est également placée entre ses points.
-
Une superficie est ce qui a longueur et largeur seulement.
-
Les extrémités d’une superficie sont des lignes.
-
Dans un plan, un angle est l’inclinaison mutuelle de deux lignes qui se touchent et qui ne sont pas placées dans la même direction.
-
Lorsqu’une ligne droite tombant sur une ligne droite fait les angles de suite égaux, chacun des angles égaux est dit droit.
-
On appelle terme ou limite ce qui est l’extrémité de quelque chose.
-
On appelle figure ce qui est compris entre une ou plusieurs limites.
-
Le cercle est une figure plane comprise dans une seule ligne qu’on appelle circonférence ; toutes les lignes droites menées à la circonférence à partir d’un unique point de ceux qui sont placés dans la figure, sont égales entre elles. Ce point se nomme le centre du cercle.
-
Les parallèles sont des lignes droites qui, étant situées dans un même plan et prolongées indéfiniment des deux côtés, ne se rencontrent jamais.
Ces « définitions » utilisent des termes non définis préalablement et semblent même parfois circulaires : la « ligne » est définie comme étant une « longueur » (dans le sens d’étendue et non de mesure), mais qu’est-ce qu’une « longueur » ? Un « angle » est défini comme étant une « inclinaison », mais qu’est-ce qu’une « inclinaison » ? Une « limite » est définie comme étant une « extrémité », mais qu’est-ce qu’une « extrémité » ? On nous dit que les « extrémités » d’une « ligne » sont des « points » et que celles d’une « superficie » sont des « lignes », mais cela ne les définit pas : ce sont seulement des relations entre les termes « point », « ligne », « superficie », « extrémité ». On ne définit rien à partir de rien.
Pour se représenter intuitivement les objets de la géométrie, il faut faire appel :
-
à notre expérience sensorielle (on fait une toute petite tache ou encoche : voilà un point ; on fait glisser la pointe du calame : voilà une ligne),
-
et à notre capacité d’abstraction (imaginez un point « qui n’a aucune partie », une ligne « sans largeur »).
Euclide n’a conservé dans ses « définitions » que la partie abstraite. Il vise la rigueur du raisonnement, sur des objets idéaux qui ont des propriétés simples.
Il donne ensuite les règles du jeu géométrique, qui nous expliquent comment on peut manipuler les termes pour faire des constructions et démonstrations. En principe, la validité d’une construction ou démonstration ne doit dépendre que du bon usage de ces règles et jamais d’un appel à une représentation intuitive des objets géométriques2 : la forme de l’argumentation peut ainsi être détachée du fond3 et jugée séparément \(-\) c’est en cela que la géométrie chez Euclide est déjà une théorie « formelle »4.
Il y a deux groupes de règles5 : les « postulats » (\(=\) « demandes ») et les « notions communes ». Il y a cinq postulats :
-
On peut mener une ligne droite d’un point quelconque à un point quelconque.
-
On peut prolonger indéfiniment une ligne droite finie, dans sa direction.
-
On peut tracer une circonférence de cercle en prenant pour rayon un segment [de droite] quelconque et pour centre l’une quelconque des extrémités de ce segment.
-
Tous les angles droits sont égaux.
-
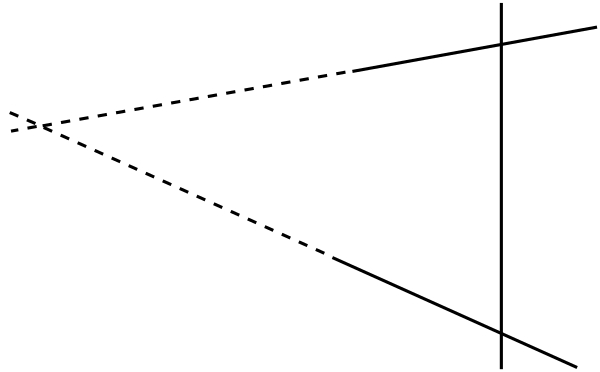
Si, une ligne droite tombant sur deux lignes droites, la somme des angles intérieurs du même côté est plus petite que deux angles droits, les deux lignes droites prolongées indéfiniment se rencontreront de ce côté-là :
Les trois premiers postulats sont les règles du jeu de la construction à la règle et au compas. Dans le premier postulat, l’unicité de la ligne droite joignant les deux points quelconques n’est pas spécifiée ; dès qu’Euclide a besoin de cette unicité (dans la preuve de la proposition 4) il la « justifie » en prétendant que si deux lignes droites joignaient deux mêmes points elles délimiteraient une aire ; or, l’une des « notions communes » (axiomes) dit que deux lignes droites ne délimitent pas une aire. L’argument serait convaincant s’il était formellement prouvé qu’en effet deux lignes droites qui joindraient deux mêmes points devraient délimiter une aire : mais cette affirmation semble reposer sur une intuition géométrique et non sur des règles claires… Il serait plus simple d’énoncer d’emblée l’unicité dans le premier postulat. D’ailleurs, il faudrait aussi affirmer celle du prolongement dans le 2e postulat (au sens où si l’on prolonge une « ligne droite finie » dans sa direction, du même côté et de deux façons, l’une des lignes prolongées est contenue dans l’autre)… De plus, dans l’utilisation de son deuxième postulat, Euclide suppose qu’en prolongeant une « ligne droite finie » dans sa direction, à partir d’une de ses extrémités, on s’éloigne constamment et sans limite de cette extrémité. Il exclut donc implicitement ce qui se passerait si on marchait tout droit devant soi sur notre planète ronde : on pourrait dire qu’on marche en « ligne droite » sur le sol et pourtant on finirait (en principe) par revenir à son point de départ (nous reviendrons, en tout cas, sur cette question).
Les deux derniers postulats semblent avoir été placés là par erreur ; d’ailleurs dans certaines versions des Éléments (y compris celle traduite par Peyrard), ils sont mis parmi les « notions communes ». Celles-ci, données juste après les postulats, décrivent les propriétés de l’égalité et de l’inégalité des grandeurs :
-
Les grandeurs qui sont égales à une même grandeur sont égales entre elles.
-
Si à des grandeurs (in)égales on ajoute des grandeurs égales, les sommes seront (in)égales.
-
Si à des grandeurs (in)égales on retranche des grandeurs égales, les restes seront (in)égaux.
-
Les grandeurs qui sont doubles d’une même grandeur sont égales entre elles.
-
Les grandeurs qui sont des moitiés d’une même grandeur sont égales entre elles.
-
Le tout est plus grand que sa partie.
-
Les choses qui peuvent être mises en coïncidence sont égales entre elles.
Ce à quoi Euclide (ou l’un de ses successeurs) ajoute :
-
Deux lignes droites ne délimitent pas une aire.
(On a vu la raison de cet ajout.)
La place naturelle du quatrième postulat (tous les angles droits sont égaux) serait plutôt parmi ces notions communes. Quant au cinquième postulat, il semble vraiment différent : il ressemble à un théorème. D’autant plus qu’Euclide en démontre la réciproque (sans utiliser le 5e postulat) : la somme de deux angles quelconques d’un triangle est toujours inférieure à deux angles droits (Proposition 17 : théorème). Certes, la réciproque d’un théorème n’est pas toujours un théorème, mais la question de la démontrabilité du 5e postulat à partir des autres règles se pose.
La géométrie absolue et le postulat des parallèles
Depuis Bolyai (1832), on appelle Géométrie absolue la géométrie d’Euclide sans son 5e postulat (et avec l’ajout implicite d’Euclide pour son 2e postulat, à savoir qu’en prolongeant indéfiniment une ligne droite dans sa direction on s’éloigne sans limite du point de départ, ainsi que d’autres hypothèses utilisées implicitement dans les Éléments et qui ont été explicitées progressivement). Les 28 premières propositions d’Euclide appartiennent à cette géométrie. La proposition 29, qui concerne les angles formés par deux parallèles avec une sécante, utilise le 5e postulat ; la proposition 30, qui dit que les droites1 qui sont parallèles à une même droite sont parallèles entre elles utilise aussi le 5e postulat. La proposition 31 appartient de nouveau à la géométrie absolue (sa preuve n’utilise pas le 5e postulat) : elle dit que par un point extérieur à une droite donnée on peut faire passer une parallèle à cette droite (Euclide en donne une construction) ; elle n’affirme pas l’unicité d’une telle parallèle mais celle-ci découle immédiatement de la proposition 30 qui, elle, repose sur le 5e postulat (comme on l’a dit). Réciproquement, on peut voir que l’unicité de la parallèle passant par le point donné implique le 5e postulat (Proclos, Commentaires sur le premier Livre des Éléments d’Euclide : 5e siècle). Donc, adjoindre à la géométrie absolue le 5e postulat (comme le faisait Euclide) équivaut à lui adjoindre le postulat des parallèles qui dit que par un point extérieur à une droite donnée, il passe une unique parallèle à cette droite.
La géométrie euclidienne, c’est la géométrie absolue plus le 5e postulat ; autrement dit, c’est la géométrie absolue plus le postulat des parallèles. Euclide a dû introduire son 5e postulat dans sa géométrie pour prouver des résultats importants qu’il ne pouvait pas établir dans le cadre de la géométrie absolue : notamment, le fait que la somme des angles d’un triangle est égale à deux droits2 (prop. 32) et le théorème du carré de l’hypoténuse qu’on appelle aujourd’hui le « théorème de Pythagore » (prop. 47).
Une géométrie non euclidienne : la géométrie hyperbolique
Des tentatives de démonstration du 5e postulat dans le cadre de la géométrie absolue ont été menées depuis l’Antiquité jusqu’au 19e siècle. Des résultats intéressants ont été obtenus3 mais le postulat lui-même n’a jamais pu être démontré.
Dans les années 1820-1830, Gauss, Lobatchevski et Bolyai se proposent (indépendamment) d’adjoindre à la géométrie absolue, non plus le postulat des parallèles, mais sa négation. En fait, ils lui adjoignent ce postulat : par un point extérieur à une droite donnée, il passe une infinité de parallèles4 à cette droite. Il est clair que cet énoncé implique la négation du postulat des parallèles, et on peut montrer que dans le contexte de la géométrie absolue il lui est équivalent (en effet, on peut voir que dès qu’il y a deux parallèles passant par le point donné, il y en a une infinité entre elles ; et que si cela se produit pour un point extérieur à une droite, alors c’est le cas pour n’importe quel point extérieur à n’importe quelle droite). Ils développent ainsi une nouvelle géométrie que Gauss qualifie de « non euclidienne » et qu’on appelle aujourd’hui la géométrie hyperbolique (il existe actuellement une infinité d’autres géométries non euclidiennes). Ils n’y trouvent aucune contradiction : au contraire, plus ils l’étudient, plus elle révèle une harmonieuse cohérence. Lobatchevski et Bolyai en publient des exposés. Voyez :
-
Lobatchevski \(+\) extraits de lettres de Gauss à Schumacher (trad. fr.) :
le texte sur Gallica -
Bolyai (trad. fr.) : le texte sur Gallica
Beltrami (1868) donne une interprétation concrète de cette géométrie5. D’autres interprétations suivront. Nous allons voir ici celle de Poincaré, qui est particulièrement frappante.
Le monde non euclidien de Poincaré
Extraits6 du chapitre 4 de l’admirable ouvrage de Poincaré La science et l’hypothèse7 (1902) :
« Des êtres dont l’esprit serait fait comme le nôtre et qui auraient les mêmes sens que nous, mais qui n’auraient reçu aucune éducation préalable, pourraient recevoir d’un monde extérieur convenablement choisi des impressions telles qu’ils seraient amenés à construire une géométrie autre que celle d’Euclide […]. »
« Pour nous, dont l’éducation a été faite par notre monde actuel, si nous étions brusquement transportés dans ce monde nouveau, nous n’aurions pas de difficulté à en rapporter les phénomènes à notre espace euclidien. Inversement, si ces êtres étaient transportés chez nous, ils seraient amenés à rapporter nos phénomènes à [leur] espace non euclidien. »
Poincaré explique comment les expériences sensorielles de ces êtres pourraient les conduire à formuler une géométrie qui leur semblerait naturelle. Pour illustrer son argument, il imagine un monde très particulier :
« Supposons, par exemple, un monde renfermé dans une grande sphère et soumis aux lois suivantes :
-
La température n’y est pas uniforme […]. Soit \(R\) le rayon de la sphère limite ; soit \(r\) la distance [d’un] point […] au centre de cette sphère. La température absolue sera proportionnelle à \(R^2-r^2\).
-
Je supposerai de plus que, dans ce monde, tous les corps aient même coefficient de dilatation, de telle façon que la longueur d’une règle quelconque [très petite par rapport au rayon \(R\) de ce monde] soit proportionnelle à sa température absolue.
-
Je supposerai enfin qu’un objet transporté d’un point à un autre, dont la température est différente, se met immédiatement en équilibre calorifique avec son nouveau milieu.
Rien dans ces hypothèses n’est contradictoire ou inimaginable. »
« Observons d’abord que, si ce monde est limité au point de vue de notre géométrie habituelle, il paraîtra infini à ses habitants. Quand ceux-ci, en effet, veulent se rapprocher de la sphère limite, ils se refroidissent et deviennent de plus en plus petits. Les pas qu’ils font sont donc aussi de plus en plus petits, de sorte qu’ils ne peuvent jamais atteindre la sphère limite. »
« Si, pour nous, la géométrie n’est que l’étude des lois suivant lesquelles se meuvent les solides invariables, pour ces êtres imaginaires, ce sera l’étude des lois suivant lesquelles se meuvent les solides déformés par ces différences de température dont je viens de parler. Sans doute, dans notre monde, les solides naturels éprouvent également des variations de forme et de volume dues à l’échauffement ou au refroidissement. Mais nous négligeons ces variations en jetant les fondements de la géométrie ; car, outre qu’elles sont très faibles, elles sont irrégulières et nous paraissent par conséquent accidentelles. Dans ce monde hypothétique, il n’en serait plus de même, et ces variations suivraient des lois régulières et très simples. »
Pour décrire ce que les habitants de ce monde verraient, Poincaré ajoute une hypothèse :
« \(-\) je supposerai […] que l’indice de réfraction soit inversement proportionnel à \(R^2-r^2\). Il est aisé de voir que, dans ces conditions, les rayons lumineux ne seraient pas rectilignes [sauf si ce sont des diamètres de la sphère], mais circulaires. »
Puisque les habitants de ce monde mesurent les longueurs avec des règles qui rétrécissent selon le facteur \(R^2-r^2\), des tout petits segments de droites situés à des distances différentes du centre de la sphère et qui pour nous auraient la même longueur, auraient pour ces êtres des longueurs différentes, inversement proportionnelles à \(R^2-r^2\). Le chemin le plus court entre deux points de ce monde, selon les mesures faites par ses habitants, ne serait pas ce que nous voyons comme une ligne droite, mais ce que nous voyons comme un arc de cercle (sauf si les deux points sont sur un même diamètre de la sphère). Plus précisément, ce qu’ils considéreraient comme des « droites » (les chemins les plus courts d’après leurs mesures, donc les plus directs pour leurs déplacements physiques), seraient ce que nous voyons comme les diamètres et les arcs de cercles qui en leurs extrémités touchent la sphère limite perpendiculairement. L’hypothèse de Poincaré sur l’indice de réfraction équivaut à supposer que dans ce monde les rayons lumineux suivraient ces « droites ». Pour les habitants de ce monde, la « distance » entre deux points serait la longueur du « segment de droite » (en leur sens) telle qu’ils la mesureraient avec leurs règles qui se dilatent et se contractent selon la température locale (il existe une formule explicite pour cette « distance »).
Poincaré décrit alors comment les « êtres sentants qui habitent ce monde imaginaire » réagiraient à leurs stimuli sensoriels et comment ils seraient amenés à construire leur géométrie. C’est une illustration sur ce cas précis de sa discussion générale antérieure. La géométrie forgée selon ces principes par les êtres de ce monde est la géométrie hyperbolique en dimension 3.
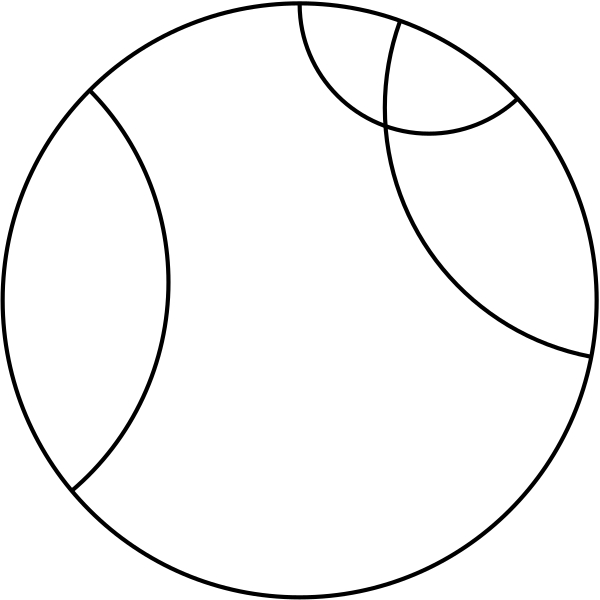
Si on remplace la sphère limite par un cercle limite, le monde étant le disque compris à l’intérieur, avec les mêmes hypothèses, on obtient la version bidimensionnelle de la géométrie hyperbolique, celle que nous avons évoquée plus haut. En fait, il s’agit d’un modèle (une interprétation concrète, dans les termes de notre géométrie habituelle) de cette géométrie non euclidienne. Il y a une correspondance entre les « points », « droites », « angles », « cercles » de cette géométrie et des objets de notre géométrie habituelle (nommés ici sans guillemets) ; elle est donnée par une sorte de dictionnaire :
-
Le « plan » : le disque à l’intérieur du cercle limite.
-
« Point » : un point du « plan ».
-
« Droite » : un diamètre du disque ou un arc de cercle dans le disque qui en ses extrémités touche le cercle limite à angle droit. Les extrémités ne font pas partie de la « droite » (elles ne sont pas dans le « plan »).
-
« Angle » (entre deux « droites ») : l’angle au sens habituel (entre les tangentes).
-
« Cercle » : un cercle au sens habituel, compris entièrement dans le « plan ».
-
Etc.
On peut prouver qu’avec cette interprétation des termes, toutes les règles de la géométrie absolue sont satisfaites8 et que par un « point » extérieur à une « droite » donnée il passe toujours une infinité de « droites » qui lui sont « parallèles » (au sens d’Euclide, c’est-à-dire qu’elles ne la rencontrent pas)9.
Le monde de Poincaré (ici, sa version bidimensionnelle) est donc bien un modèle de la géométrie hyperbolique en termes d’objets de la géométrie euclidienne : disque, points, diamètres, arcs de cercles… Cela suppose, bien entendu, que notre géométrie habituelle, euclidienne, est cohérente1 (si elle ne l’est pas, le « modèle » de géométrie hyperbolique qu’on y a construit s’écroule avec elle).
Une preuve d’indécidabilité
L’existence d’un tel modèle montre que dans la géométrie absolue on ne peut pas démontrer le postulat des parallèles (ou le 5e postulat : c’est équivalent). En effet, supposons qu’il existe une preuve de ce postulat, n’utilisant que les règles de la géométrie absolue. On parle ici d’une preuve formelle, c’est-à-dire qu’on y manipule les termes de la théorie (« points », « droites », etc.) selon les règles explicitement énoncées (les règles du jeu de la géométrie absolue2), indépendamment de toute interprétation particulière. Une telle preuve serait donc valable pour tout modèle de la géométrie absolue. En particulier, le postulat des parallèles serait valable pour les « points » et « droites » du monde de Poincaré, ce qui n’est pas le cas.
Notons \(G\) la géométrie absolue, \(P\) le postulat des parallèles, \(\neg{P}\) sa négation. Alors la géométrie euclidienne est \(G+P\), la géométrie hyperbolique est \(G+\neg{P}\). Comme on suppose que la géométrie euclidienne est cohérente, la géométrie absolue (qui en est une partie) l’est à fortiori. On vient de voir que \(P\) n’est pas démontrable dans \(G\). Mais \(\neg{P}\) ne l’est pas non plus ; car sinon il y aurait une contradiction dans la géométrie euclidienne \(G+P\) (on y aurait \(P\) comme postulat et \(\neg{P}\) comme théorème).
Conclusion : si la géométrie euclidienne est cohérente, \(G\) l’est aussi et on ne peut y prouver ni \(P\) ni \(\neg{P}\) : on dit que \(P\) (et, aussi bien, \(\neg{P}\)) est indécidable dans \(G\).
La géométrie sphérique
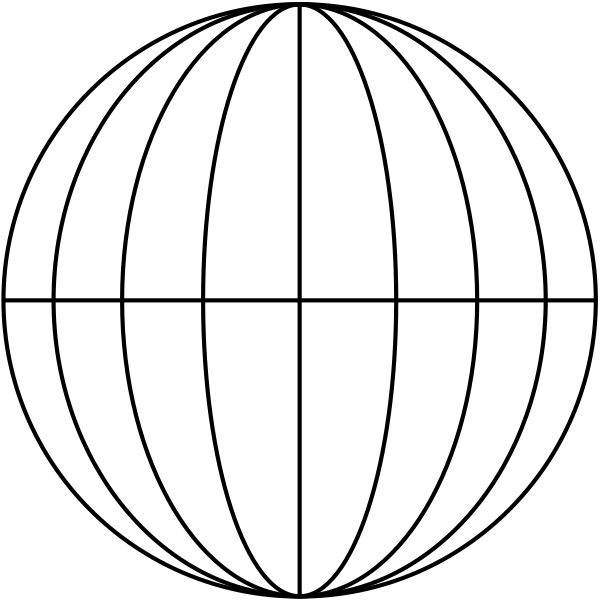
J’ai dit que nous reviendrions sur la géométrie sphérique. On considère une planète sphérique, sans relief, sans océan. On a longtemps cru que notre planète était plate : il n’y a rien de choquant à appeler cette planète « le plan ». Mais si on y marche tout droit devant soi, on finit par revenir à son point de départ, après avoir parcouru un grand cercle de la planète, c’est-à-dire un cercle de même centre qu’elle (et donc de même rayon, puisque tracé sur elle). Les « droites » de la géométrie sphérique sont ces grands cercles ; les « points » sont les points de la sphère ; les « angles » au point de croisement de deux « droites » sont les angles au sens usuel… On peut voir que la plupart des règles de la géométrie absolue sont satisfaites, mais pas toutes. Par exemple, la dernière « notion commune » n’est plus vraie : deux segments de « droites » peuvent délimiter une aire (pensez à un fuseau délimité par deux demi-grands cercles de mêmes extrémités).
Et l’unicité dans le premier postulat, que cette « notion commune » était censée garantir, mais qui devait plutôt être supposée, n’a plus toujours lieu ici : par deux « points » diamétralement opposés, il passe une infinité de « droites » ! De plus, contrairement à ce qui se passait en géométrie absolue, quand on prolonge indéfiniment une « ligne droite finie » dans sa direction en géométrie sphérique, on ne s’éloigne pas indéfiniment du point de départ ; au contraire, on y revient et on repasse indéfiniment par les mêmes points. Il y a donc des théorèmes de la géométrie absolue qui ne sont plus valables ici. Notamment :
-
Il n’est pas vrai que la somme des angles d’un « triangle » soit toujours inférieure ou égale à deux droits : au contraire, elle y est toujours supérieure.
-
Le « théorème de Pythagore » est faux pour les « triangles » rectangles de la sphère (imaginez un « triangle » dont un sommet est au pôle nord et les deux autres sur l’équateur).
En géométrie absolue, le postulat des parallèles et le 5e postulat étaient équivalents. Ici :
-
Le postulat des parallèles est faux car en géométrie sphérique il n’y a pas de « parallèles », toutes les « droites » se coupent !
-
Le 5e postulat n’est pas faux, mais alors qu’en géométrie euclidienne les deux « droites » ne se coupent que du côté où sont les angles intérieurs dont la somme est inférieure à deux droits, en géométrie sphérique elles se coupent aussi de l’autre côté (au point diamétralement opposé) !
La géométrie sphérique est donc une autre sorte de géométrie « non euclidienne ».
Si on identifie les points diamétralement opposés deux à deux, on obtient un modèle d’une géométrie encore différente, dans laquelle on retrouve le fait que par deux « points » distincts il ne passe qu’une seule « droite » ; dans l’énoncé du 5e postulat, les deux « droites » se coupent du côté où sont les angles dont la somme est inférieure à deux droits et aussi de l’autre côté mais maintenant au même point ! Et là aussi, pas de « parallèles » : deux « droites » quelconques se coupent, mais toujours en un seul « point ».
Ni vraies ni fausses
Concluons par une citation du chapitre 3 de La science et l’hypothèse :
« Dès lors, que doit-on penser de cette question : la géométrie euclidienne est-elle vraie ? Elle n’a aucun sens. Autant demander si le système métrique est vrai et les anciennes mesures fausses ; si les coordonnées cartésiennes sont vraies et les coordonnées polaires fausses. Une géométrie ne peut pas être plus vraie qu’une autre ; elle peut seulement être plus commode. »
Poincaré ajoute que la géométrie euclidienne est objectivement plus simple que les non euclidiennes (par exemple, la somme des angles y est la même dans tous les triangles) et « qu’elle s’accorde assez bien avec les propriétés des solides naturels ». Ce qui l’amène à penser qu’elle « restera la plus commode » dans notre monde. La Relativité générale (Einstein, 1916) a montré que cela n’est pas vrai si on étudie les forts champs de gravitation : il est plus commode de les décrire dans une géométrie qui n’est pas euclidienne (et qui est différente de celles évoquées ci-dessus)… En fait, notre monde ressemble un peu à celui de Poincaré ; mais ce n’est pas la température qui fait varier la longueur de nos règles (et aussi, d’ailleurs, la cadence de nos horloges) : c’est la gravitation. De plus, la loi qui détermine ces effets n’est pas aussi simple que le \(T=R^2-r^2\) du monde de Poincaré (c’est en fait une équation aux dérivées partielles qui relie, en chaque point de l’espace-temps, la géométrie à la concentration et au mouvement de la masse présente)…