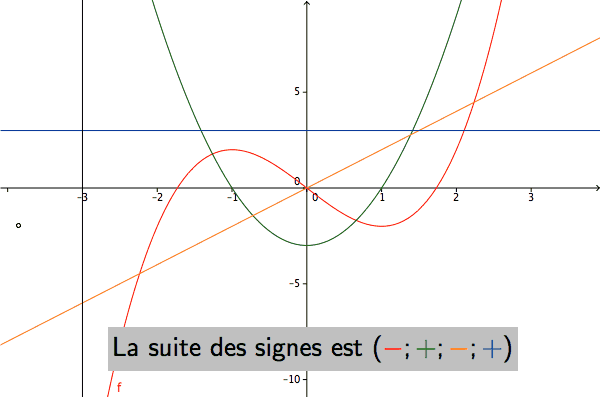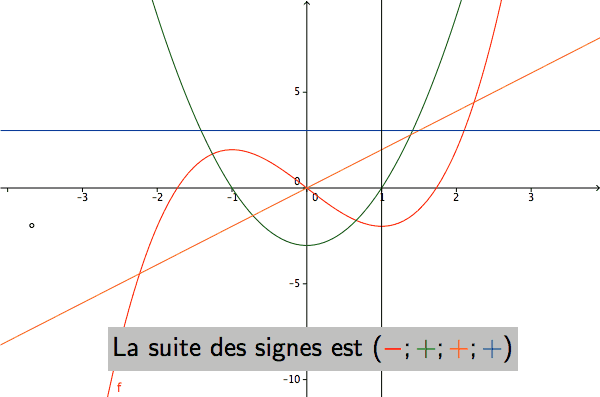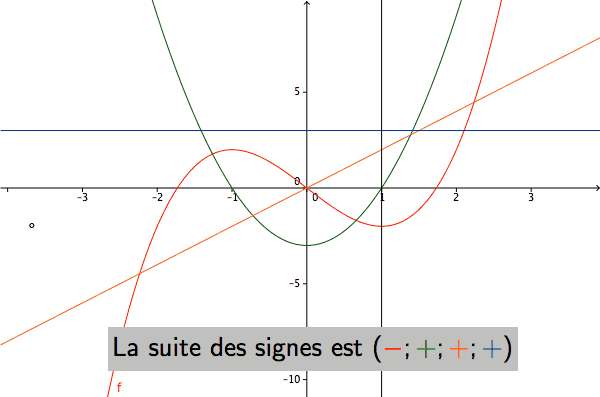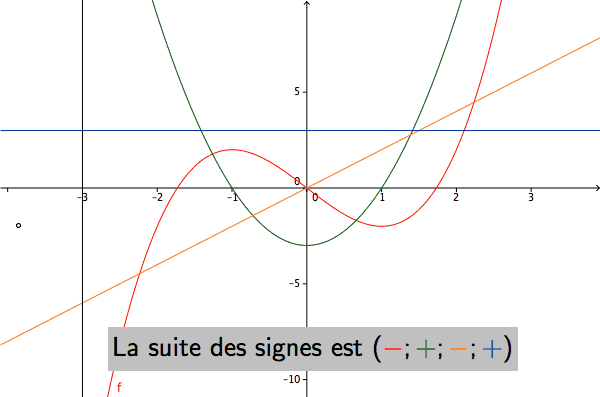
Pour un polynôme de degré quelconque donné, existe-t-il une méthode simple permettant de calculer le nombre de racines réelles comprises entre deux bornes?
Pour un polynôme de degré quelconque donné, existe-t-il une méthode simple permettant de calculer le nombre de racines réelles comprises entre deux bornes ? À cette question, le jeune Charles Sturm (1803-1855), alors tout juste âgé de vingt-cinq ans, donne une réponse d’une étonnante simplicité dans son mémoire sur la Résolution des équations numériques, lu le 25 mai 1829 à l’Académie Royale des Sciences de Paris.
Ce problème avait en effet occupé quelques grands mathématiciens sans qu’ils y fournissent une réponse satisfaisante. Descartes (1596-1650), dans sa Géométrie publiée en 1637 [3, p.446], donne une réponse partielle : le nombre de racines positives d’une équation P(x)=0 où P est un polynôme à coefficients réels est au plus égal au nombre de changements de signe dans la suite des coefficients de P, une fois bien sûr que P a été réduit et ordonné (c’est-à-dire, mis sous la forme d’une somme de monômes de degrés strictement décroissants).
La partie de la règle de Descartes concernant les racines négatives (les racines « fausses ») est inexacte1, à moins de faire apparaître les termes manquants et d’attribuer un signe (peu importe lequel) aux coefficients nuls.
Pour une démonstration de cette règle, il faudra attendre Gauss2, qui publie dans le Journal de Crelle de 1828 une preuve rigoureuse de ce théorème, en l’accompagnant du résultat complémentaire suivant : le nombre de racines positives a la même parité que le nombre de changements de signe.
Plus d’un siècle après, Lagrange (1736-1813) cherche lui aussi à résoudre ce problème, et il propose une solution qui consiste à effectuer un certain nombre d’opérations sur les coefficients. Cette méthode, qui utilise l’équation aux carrés des différences3, permet certes d’apporter une réponse complète au problème, mais elle présente, comme s’en aperçoit Sturm, un défaut majeur :
Cette méthode, considérée sous un point de vue purement théorique, ne laisse rien à désirer du côté de la rigueur. Mais l’application, la longueur des calculs nécessaires pour former l’équation aux carrés des différences, et la multitude des substitutions qu’on peut avoir à effectuer, la rendent presque impraticable ; [8] p.274
En effet, les calculs deviennent rapidement monstrueux, et Lagrange lui-même, qui qualifie d’ailleurs sa méthode de « presque impraticable », renonce à l’utiliser pour des équations de degré supérieur à cinq. De son côté, Joseph Fourier (1768-1830) généralise la règle de Descartes :
Les différentes méthodes qui ont été proposées pour arriver à ce but sont trop connues pour qu’il soit nécessaire de les rappeler ici. Aucune ne peut être comparée, sous le double rapport de la simplicité et de l’exactitude, à celle que M. Fourier a depuis longtemps découverte, et qui est fondée sur une proposition générale, dont la règle des signes de Descartes n’est qu’un cas particulier.(…) C’est en m’appuyant sur les principes qu’il a posés, et en imitant ses démonstrations, que j’ai trouvé les nouveaux théorèmes que je vais énoncer. [7] p.419
Les méthodes que Fourier emploie sont très différentes de celles de Lagrange et font partie de ce qu’il appelle l’analyse algébrique1. En fait ce sont les équations algébriques qui constitue le liant de cette « méthode »2, et pour les étudier, il a recours aussi bien à des méthodes issues de l’algèbre au sens où Lagrange l’entend, qu’à des méthodes mettant en jeu des notions telles que la continuité. Cependant, si les méthodes employées par Fourier sont d’une grande « simplicité », le résultat perd en généralité et la réponse donnée est incomplète.
Le théorème que Sturm va proposer peut ainsi finalement être vu comme le résultat de la confrontation entre les travaux de Lagrange portés par une volonté de généralité avec ceux de Fourier, utilisant aussi des méthodes analytiques, et recherchant l’effectivité.
Énoncé et premier exemple
Il est maintenant temps de regarder précisément ce que dit le théorème de Sturm, qui permet donc de calculer le nombre de racines réelles d’un polynôme comprises entre deux bornes a et b.
Soit \[ P(x)=x^n+a_1x^{n-1}+\dots\ +a_n \in \mathbb{R}[x] \] On construit la suite \( (P_n) \) de polynômes de la façon suivante : on note \(P_0=P \), \(P_1=P' \) et ensuite on effectue la division euclidienne de \(P_0 \) par \(P_1 \) et on note \(P_2 \) l’opposé du reste obtenu.
Diviser des polynômes n’est pas plus difficile, voire plus simple, que de diviser des nombres entiers ; en effet, l’indéterminée « \(X\) » y joue le rôle du nombre 10 dans l’arithmétique décimale, avec une simplification : aucune « retenue » n’est nécessaire. En d’autres termes, tandis que dans l’arithmétique entière on a \((9\times 10+7)+10=1\times 100+7\), avec les polynômes on pose simplement \((9\times X+7)+X=10\times X+7\). Ci-dessous, pour comparaison, des exemples des deux divisions utilisant les mêmes « chiffres ».
\[ \begin{array}{r|l} 6X^3 + 2X^2 + \phantom{6}X + 3 & \phantom{6}X^2 + X + 1\\ \hline \phantom{1^{1^1}}-6X^3 - 6X^2 - 6X \phantom{+11} & 6X\phantom{{}^2} - 4 \\ \hline \phantom{1^{1^1}}-4X^2 - 5X + 3 \\ 4X^2 + 4X + 4 \\ \hline -X +7 \end{array} \]
\[ \begin{array}{r|l} 6213 & 111\\ \hline 663 & 55 \\ \hline 108\\ \end{array} \]
Les deux divisions relèvent de formalismes très similaires : \[ \begin{array}{ll} \text{Dans $\mathbf Z$ :}&a=bq+r, |r| < |b|\\ \text{Dans $\mathbf Q[X]$ :}&A=BQ+R, \deg(R) < \deg(B)\text{ ou }R=0\\ \end{array} \]
Dans le contexte que nous étudions ici, nous avons cependant à diviser par des polynômes dérivés, dont le coefficient dominant n’est pas 1 ; cela a pour désagréable conséquence d’introduire des dénominateurs dans l’algorithme, et d’obliger à un calcul souvent volumineux sur des fractions.
On recommence ainsi le processus en définissant \(P_m\) comme l’opposé du reste de la division euclidienne de \(P_{m-2}\) par \(P_{m-1}\) jusqu’à obtenir un reste de degré 0 (ce qui arrive en moins de \( n \) itérations car la suite des degrés des polynômes est strictement décroissante). On a ainsi obtenu la suite finie \(P_0,P_1,\dots\ ,P_k\), appelée suite de Sturm. En notant \( C_x \) le nombre de changements de signe dans la suite \(S_x= (P_0(x),P_1(x),\dots\ ,P_k(x)) \), on obtient alors le théorème de Sturm, qui affirme que le nombre de racines de \(P\) sur \( [a;b] \) est égal à \( C_a-C_b \). Ce théorème s’étend d’ailleurs facilement au cas où \(a=-\infty\) et \(b=+\infty\).
Reprenons l’exemple que donne Sturm lui-même dans son mémoire de 1835 : \[P(x)=x^3-2x-5\] On a alors les deux premiers termes de la suite : \begin{align*} P_0(x)&=x^3-2x-5\\ P_1(x)&=3x^2-2 \end{align*}
On effectue la division euclidienne de \(3P_0\) par \(P_1\). Le coefficient 3 est là pour que l’on puisse conserver des coefficients entiers : comme le justifie Sturm, la multiplication d’un des termes de la suite par un coefficient positif ne change rien aux signes de ces termes. Or seul le signe de ces termes importe ici. On obtient alors :
\[3x^3-6x-15=(3x^2-2)x-(4x+15)\] et ainsi \(P_2(x)=4x+15\). On effectue ensuite la division euclidienne de \(16P_1\) par \(P_2\) et on obtient : \[48x^2-32=(4x+15)(12x-45)-(-643)\] et ainsi on pose \(P_3(x)=-643\). Comme \(P_3\) est un réel différent de zéro, on peut déjà affirmer que \(P\) n’a pas de racines doubles1. Pour obtenir le nombre total des racines de \(P\), on applique le théorème précédent avec \(a=-\infty\) et \(b=+\infty\). On obtient les deux suites de signes suivantes :
\begin{align*} S_{-\infty}&=(-,+,-,-)\\ S_{+\infty}&=(+,+,+,-)\\ \end{align*}
Ainsi le nombre de racines réelles est :
\[C_{-\infty}-C_{+\infty}=2-1=1\] Il y a donc une unique racine réelle2.
Sturm commence ainsi l’article de 1829 qui expose pour la première fois ce théorème :
La résolution des équations numériques est une question qui n’a cessé d’occuper les géomètres depuis l’origine de l’algèbre jusqu’à nos jours. La véritable difficulté de ce problème se réduit, comme on le sait, à trouver, pour chaque racine réelle de l’équation proposée, deux limites, entre lesquelles cette racine soit seule comprise. [7]
On voit donc qu’il s’agit d’un procédé effectif, algorithmique, qui répond à une question qui s’énonce simplement et qui a été longtemps débattue. Comme le montre H. Sinaceur [6], ce théorème a une popularité immédiate : il est commenté et repris dès 1829, et apparaît au xix\(^\text{e}\) siècle dans les ouvrages généraux d’algèbre, aussi bien en France que dans le reste de l’Europe et aux États-Unis1. En fait, l’intérêt pour ce théorème va croître jusqu’au milieu des années 1850, pour ensuite se stabiliser jusqu’à la fin du xix\(^\text{e}\) siècle, et s’évanouir complètement dans les années 1930. C’est donc un théorème presque oublié dont nous allons maintenant présenter la démonstration.
Démonstration du théorème par Sturm
En 1835, six ans après avoir énoncé son théorème, et quelques années après la publication de plusieurs démonstrations d’autres mathématiciens1, Sturm donne sa propre preuve dans un Mémoire sur la résolution des équations numériques [8]. Ce que nous souhaitons faire ici, ce n’est pas donner une démonstration concise et moderne, mais bien reprendre, point par point, la démonstration que donne Sturm de son théorème en 1835 dans son mémoire [8]. En voici le plan général :
-
Les six premiers chapitres du mémoire, qui constituent l’essentiel de ce qui nous intéresse ici, énoncent le théorème et donnent sa démonstration.
-
Les six chapitres suivants présentent quelques astuces calculatoires pour abréger les applications du théorème.
-
Les chapitre 13 et 14 traitent, dans certains cas, du dénombrement des racines imaginaires : il s’agit ici aussi de simplifier, lorsque cela est possible, la détermination du nombre de racines, réelles et imaginaires.
-
Le chapitre 17 donne 3 exemples sur lesquels Sturm fait fonctionner l’ensemble de ce qu’il a présenté.
-
Le chapitre 18 étend le théorème au cas des racines multiples.
Nous allons donc regarder en détail les six premiers paragraphes. Prenons comme le fait Sturm, et avec ses notations, l’équation suivante :
\[V=a_mx^m+a_{m-1}x^{m-1}+a_{m-2}x^{m-2}+\dots\ +a_1x+a_0=0\] où \(V\) est un polynôme dont les coefficients sont réels (équation numérique). Soit \(V_1=V'\), on effectue la division euclidienne en modifiant les restes comme on l’a vu précédemment et on obtient :
\begin{align*} V&=Q_1V_1-V_2 &\text{ où } \deg V_2 \lt \deg V_1 \\ V_1 &= Q_2V_2-V_3 &\text{ où }\deg V_3 \lt \deg V_2 \\ \dots\ &=\dots\ \\ V_{r-2}&=Q_{r-1}V_{r-1}-V_r &\text{ où }\deg V_{r} \lt \deg V_{r-1}\end{align*}
où \(\deg V_r=0\) (\(V_r\) est un nombre réel). Pour éviter le cas de racines multiples, Sturm choisit dans un premier temps2 de supposer \(V_r\ne 0\).
Il énonce ensuite son théorème, et affirme que le nombre de racines réelles de \(V\) comprises entre \(a\) et \(b\) est la différence :
\begin{align*} &\textit{Nombre de changements de signe dans la suite }\left(V(a),V_1(a),\dots\ ,V_r(a)\right)\\ -&\textit{Nombre de changements de signe dans la suite }\left(V(b),V_1(b),\dots\ ,V_r(b)\right) \end{align*}
Le principe consiste à examiner comment varie le nombre de changements de signe dans la suite \(\left(V(x),V_1(x),\dots\ ,V_r(x)\right)\) lorsque \(x\) varie .
Lorsque \(x\) croît, un changement apparaît dans la suite des signes uniquement si \(V\) ou l’un des \(V_i\) change de signe, et donc s’annule. Sturm utilise ici implicitement le fait que les \(V\) sont continues et le théorème de Bolzano3. Sturm traite alors les deux situations suivantes :
Situation 1 : soit \(c\in [a;b]\) tel que \(V(c)=0\).
On a alors par hypothèse \(V_1(c)\ne 0\), car sinon \(c\) serait racine multiple de \(V\). La continuité de \(V_1\) nous permet d’affirmer que l’on peut trouver \(u>0\) suffisamment petit pour que \(V_1\) reste de signe constant sur \([c-u;c+u]\). On peut alors appliquer la formule de Taylor4 :
\begin{align*} V(c+u)&=V(c)+V'(c)u+\dfrac{V''(c)}{2}u^2+o(u^2)\\ &=u\left[V'(c)+\dfrac{V''(c)}{2}u+o(u)\right] \end{align*}
et conclure que pour \(u>0\) suffisamment petit \(V(c+u)\) aura le même signe que \(V'(c)\), et donc que \(V'(c+u)\).
On rappelle que \(V_1=V'\). Ainsi \(V\) a le même signe que \(V_1\) pour \(c+u\). De même, en posant \(u=-u\), on voit que \(V\) a le signe contraire de celui de \(V_1\) pour \(c-u\). On peut résumer la situation avec les deux tableaux suivants :
| \(V\) | \(V_1\) | |
| \(c-u\) | \(-\) | \(+\) |
| \(c\) | 0 | \(+\) |
| \(c+u\) | \(+\) | \(+\) |
ou
| \(V\) | \(V_1\) | |
| \(c-u\) | \(+\) | \(-\) |
| \(c\) | 0 | \(-\) |
| \(c+u\) | \(-\) | \(-\) |
On voit que dans les deux cas on perd une « variation de signe » lorsque l’on passe de \(c-u\) à \(c+u\). Si aucun autre \(V_i\) (\(i=2,\dots\ ,r\)) ne s’annule en \(c\), il y a donc lorsque \(x\) croît de \(c-u\) à \(c+u\) la perte d’un changement de signe.
Situation 2 : Soit \(c\in [a;b]\) tel qu’il existe \(1\leq i\leq r-1\) pour lequel \(V_i(c)=0\).
Comme on a l’égalité \[(E) \qquad V_{i-1}=Q_iV_i-V_{i+1}\] on ne peut avoir \(V_{i-1}(c)=0\) ni \(V_{i+1}(c)=0\). En effet, par construction tous les \(V_i(c)\) seraient égaux à 0, et donc aussi \(V_r\), ce qui n’est pas possible. Par \((E)\) on a de plus :
\[V_{i-1}(c)=-V_{i+1}(c)\] donc \(V_{i-1}(c)\) et \(V_{i+1}(c)\) sont de signes contraires. Pour \(u>0\) suffisamment petit on a donc
| \(V_{i-1}\) | \(V_i\) | \(V_{i+1}\) | |
| \(c-u\) | \(+\) | \(\pm\) | \(-\) |
| \(c\) | \(+\) | 0 | \(-\) |
| \(c+u\) | \(+\) | \(\mp\) | \(-\) |
ou
| \(V_{i-1}\) | \(V_i\) | \(V_{i+1}\) | |
| \(c-u\) | \(-\) | \(\pm\) | \(+\) |
| \(c\) | \(-\) | 0 | \(+\) |
| \(c+u\) | \(-\) | \(\mp\) | \(+\) |
Dans tous les cas, lors du passage de \(c-u\) à \(c+u\) il n’y aura pas de variation dans le nombre de changements de signe (on a un tableau similaire pour \(V_{i-1}(c)
Conclusion
Ainsi le nombre de changements de signe de la suite \(\left(V(x),V_1(x),\dots\ ,V_r(x)\right)\) diminue d’une unité si et seulement si \(x\) « passe » par une racine de \(V\). Si \(x\) croît de \(a\) à \(b\), la suite \(\left(V(x),V_1(x),\dots\ ,V_r(x)\right)\) perdra autant de changements de signe qu’il y aura de valeurs pour lesquelles \(V\) s’annulera.
Conclusion
Voilà donc la démonstration que Sturm propose en 1835. Sur quoi repose-t-elle ? En grande partie sur le théorème de Bolzano et sur une méthode consistant à effectuer de « petits accroissements », tous deux appliqués sur une suite de fonctions auxiliaires que Sturm construit à partir de l’algorithme d’Euclide, mais dont il n’extrait pas explicitement les propriétés fondamentales qui permettent à sa méthode de fonctionner, même s’il est, comme le seront aussi ses principaux lecteurs, parfaitement conscient de ces conditions. Ces dernières sont données, par exemple, par Heinrich Weber (1842-1913) dans le premier tome de son célèbre Lehrbuch der Algebra :
Soit une suite de polynômes \(f, f_1,\dots\ ,f_m\) où \(f\) est supposé sans racines multiples et \([a;b]\) un intervalle tel que ni \(a\) ni \(b\) ne soit une racine de \(f\). Alors pour être utilisée dans le théorème de Sturm cette suite doit respecter les conditions suivantes5 :
-
Deux fonctions consécutives ne s’annulent pas pour une même valeur de l’intervalle \([a;b]\).
-
La fonction \(f_m\) ne s’annule pour aucune valeur de l’intervalle \([a;b]\).
-
Si \(f_i(\alpha)=0\), alors \(f_{i-1}(\alpha)\) et \(f_{i+1}(\alpha)\) sont de signes contraires.
-
Si \(f(\alpha)=0\), alors \(f_{1}(\alpha)\) a le même signe que \(f'(\alpha)\).
À partir de ces conditions, un grand nombre de suites de Sturm peuvent être construites. Sturm le savait dès 1829, et il affirmait que l’on pouvait « en former une infinité d’autres qui jouissent des même propriétés ».
On peut voir dans la seconde partie du mémoire de 1835, que nous ne développerons pas ici, d’autres considérations sur ces suites de Sturm. Le choix de Sturm de prendre comme suite de fonctions les restes modifiés de l’algorithme d’Euclide peut sembler, à première vue, miraculeux. Et de fait, comme le rapporte H. Sinaceur, certains de ses contemporains ont pu qualifier son travail de « divination », « d’illumination de l’esprit »6. Mais réduire ce choix à quelque inspiration « géniale » est pour le moins trompeur. Sturm a travaillé en étroite collaboration avec Fourier et a beaucoup lu les écrits de Lagrange : c’est bien à partir des travaux de ce dernier qu’il a conçu son théorème.
Exemples
Pour le polynôme \(P=X^3-3X\), la suite de Sturm est représentée ci-dessous1
Prenons le polynôme \(P_0=x^6-1000x^5+100x+1\). L’algorithme donne a priori des polynômes à coefficients fractionnaires, mais on peut remultiplier les \(P_i\) en cours de route par des facteurs entiers positifs sans altérer aucunement la prise de décision. On obtient :
\[ \begin{array}{l} P_1=6x^5-5000x^4+100\\ P_2=-(9\,P_0) \bmod P_1=1250000x^4 - 750x - 25009\\ P_3=-(625000\,P_1) \bmod P_2=-2250x^2+ 1799973x + 22500\\ P_4=-(5\,P_2) \bmod P_3=-3199956000656239x - 39999424883955\\ P_5=-P_3\bmod P_4= -\frac{35156734157}{500000000000000}\\ \end{array} \]
Soit \(L(x)\) la liste des signes de ces polynômes au point \(x\). En \(-\infty\), en examinant les coefficients dominants et les puissances impaires on obtient \([1,-1,1,-1,1,-1]\), soit 5 changements de signe.
En \(+\infty\), on trouve de même \([1,1,1,-1,-1,-1]\) avec 1 changement de signe; \(P\) admet donc 4 racines réelles.
On peut affiner et en savoir plus sur les racines de \(P\), car les coefficients de \(P\) ne sont pas « très grands ». Si \(x\) est racine de \(P\) avec \(|x|\geq 1\), on a \(x^6=1000x^5-100x-1\), ce qui permet de majorer un peu :
\[ x^6\leq 1000(|x|^5+|x|+1) \leq 1000(|x|^5+|x|^4+|x|^3+|x|^2+|x|+1)=1000\frac{|x|^6-1}{|x|-1} \]
d’où l’on tire en « chassant le dénominateur »: \(|x|^7\leq 1001|x|^6\) soit \(|x|\leq 1001\).
On reprend alors la méthode de Sturm avec diverses valeurs « bien choisies » :
\(L(0)=[1,1,-1,1,-1,-1]\) (3 changements de signe, donc 2 racines négatives et 2 positives)
\(L(-1)=[1,-1,1,-1,1,-1]\) (5 changements de signe, donc 2 racines dans \([-1;0]\))
\(L(-0.5)=[-1,-1,1,-1,1,-1]\) (4 changements de signe, donc 1 racine entre -1 et \(-\frac12\) et l’autre entre \(-\frac12\) et 0)
\(L(1)=[-1,-1,1,1,-1,-1]\) (2 changements de signe, donc une racine entre 0 et 1)
\(L(1000)=[1,1,1,-1,-1,-1]\) (1 changement de signe, donc une racine entre 1 et 1000).
Un logiciel de calcul numérique donne pour valeurs approchées des quatre racines \[[-0.55973436768618967,-0.010000001000037173,0.56489347092855269,999.9999999998999]\]
Cette réponse du logiciel peut sembler précise mais elle n’est pas garantie, alors que celle que fournit la méthode de Sturm a une authentique valeur démonstrative.
Bibliographie
[1] Crelle, A. (1835). Die Sätze von Fourier und Sturm zur Theorie der algebraischen Gleichungen. Journal für die reine und angewandte Mathematik, 13:119–144.
http://www.digizeitschriften.de/dms/toc/?PID=PPN243919689_0013
[2] Davies, C. (1844). Elements of algebra, including Sturm’s theorem. AS Barnes.
https://archive.org/details/elementsofalgebr1844davi/page/354
[3] Descartes, R. (1987). Descartes, Discours de la méthode plus la dioptrique les météores et la géométrie. Tours, Fayard.
[4] Fourier, J. B. J. (1830). Analyse des équations déterminées, volume 1. Firmin Didot.
https://gallica.bnf.fr/ark:/12148/bpt6k1057816b.image
[5] Mayer and Choquet (1832). Traité élémentaire d’algèbre. Bachelier, Paris.
https://gallica.bnf.fr/ark:/12148/bpt6k26777b/f494.item
[6] Sinaceur, H. (1991). Corps et Modèles: essai sur l’histoire de l’algèbre réelle. Vrin - Mathésis (Paris).
[7] Sturm, C. (1829). Analyse d’un mémoire sur la résolution des équations numériques. Bulletin de Férussac, 11:419–422.
[8] Sturm, C. (1835). Mémoire sur la résolution des équations numériques. Mémoire présenté par divers Savants étrangers à l’Acad. roy. sc., section math.phys., 6:273–318.
[9] Weber, H. (1895). Lehrbuch Der Algebra, Band 1. Braunschweig.
https://gallica.bnf.fr/ark:/12148/bpt6k99500c/f6.image.texteImage