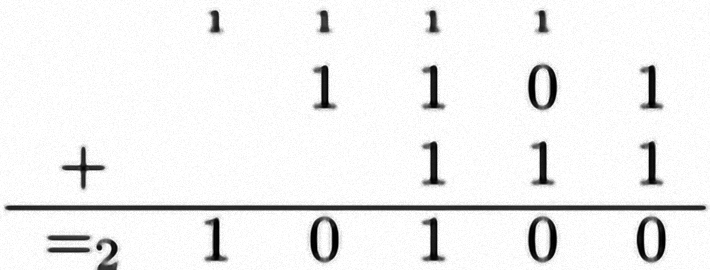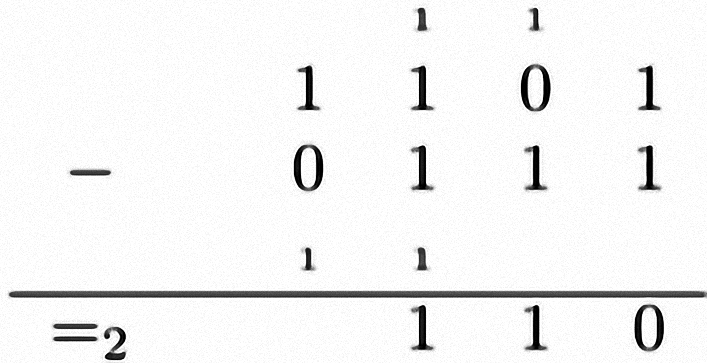LES ordinateurs manipulent des informations qui sont représentées à l’aide de 0 et de 1. Ces informations, dites binaires, permettent de représenter les nombres entiers et de faire des calculs.
Ce numéro double 525-526 du fameux Bulletin Vert de l'APMEP est le dernier d'une longue série. Le Bulletin est remplacé par une nouvelle publication : Au fil des maths - Le bulletin de l’APMEP à retrouver en suivant le lien.
Dans cet article, nous proposons une activité de découverte de la représentation des nombres en binaire, accessible dès le début du collège. Nous présentons un retour d’expérience au collège. Nous donnons aussi des activités d’approfondissement (conversion et opérations arithmétiques).
Introduction
La représentation binaire des informations est à la base du fonctionnement des ordinateurs. Ce savoir est considéré essentiel à tous les niveaux d’enseignement par les experts et les didacticiens de l’informatique : de l’école primaire1 à la classe de terminale scientifique dans l’enseignement de spécialité ISN (Informatique et Sciences du Numérique). Pourtant, elle n’est pas sans présenter des difficultés d’apprentissage2 à tous les niveaux d’étude.
L’intérêt de cette représentation est qu’elle n’utilise que deux symboles (0 et 1), ce qui la rend proche des composants électroniques des ordinateurs qui possèdent deux états. L’inconvénient de cette représentation — au moins du point de vue des êtres humains — est qu’elle prend beaucoup de place. Ainsi, l’écriture en binaire du nombre entier 42 utilise au moins six symboles : 101010. Pour que les élèves se forgent une image mentale correcte du fonctionnement d’un ordinateur, il est important de leur expliquer comment une machine peut, avec uniquement deux symboles, représenter toutes sortes d’informations, et entre autres des nombres. La plupart des activités proposées sur la représentation binaire des nombres se concentre sur la façon de changer de base, c’est-à-dire sur le passage de la représentation décimale (en base 10) habituelle à la représentation binaire (en base 2) et vice versa. L’objectif de cet article est de décrire une activité menant à la découverte de la représentation binaire d’un nombre entier, afin de favoriser l’apprentissage d’un des concepts fondamentaux de l’informatique. Cette activité, accessible dès le début du collège, repose sur un tour de magie, qui consiste à deviner un nombre en demandant s’il est présent ou non sur des cartes magiques. Ensuite, une fois la notion de représentation binaire des nombres entiers acquise, nous présentons d’autres activités permettant d’aller plus loin dans la manipulation des nombres en base 2 (conversion et opérations arithmétiques).
Cet article est basé sur une partie des travaux du groupe « Faire de l’informatique sans ordinateur à l’école et au collège » de l’IREM de Clermont-Ferrand et de la Maison pour la Science en Auvergne (MPSA). Ce groupe est composé d’enseignants du premier degré, d’enseignants de mathématiques du second degré et d’universitaires (informaticiens, mathématiciens et didacticiens de l’informatique). L’ensemble des ressources produites par ce groupe a été testé dans des classes de plusieurs niveaux en primaire et en collège, a été présenté plusieurs fois en formation continue à la MPSA et est téléchargeable en libre accès3.
L’intérêt porté aux nombres binaires est un domaine ancien comme le montrent les mathématiques antiques4, avec la multiplication binaire présente sur un papyrus datant de 1700 ans av. J.-C., l’analyse d’un texte de Gottfried Wilhelm Leibniz5, ou encore l’ouvrage sur la préhistoire des ordinateurs6. Dans l’ouvrage de référence pour la spécialité ISN en Terminale S7, les auteurs montrent comment représenter des nombres entiers et à virgule. De plus, ils proposent un algorithme pour Ajouter deux nombres exprimés en base deux. Ce thème est également abordé dans le livre pour les classes préparatoires8 au travers du chapitre sur la représentation des nombres. L’initiation au binaire est considérée comme un incontournable dans la plupart des réflexions sur les notions à enseigner lors de l’alphabétisation à l’informatique. Les cursus des différents pays et de différents niveaux de classe la mentionnent, des moyens pédagogiques ont été depuis fort longtemps inventés pour tenter d’en faciliter la compréhension. Ainsi, dans la proposition de curriculum élaborée par la Computer Science Teachers Association9, les nombres binaires figurent au niveau collège dans la thématique science informatique et communauté. L’association propose un certain nombre d’activités pédagogiques, dont celle présentée dans cet article. Un objectif généralement partagé est que les élèves doivent comprendre comment les 0 et les 1 peuvent être utilisés pour représenter l’information, comme les images numériques ou les nombres10.
Ainsi, on peut trouver de multiples exemples de mise en oeuvre d’un tel enseignement. Une première approche du tour de magie avec les cartes est proposée par11. Sur le site http://csunplugged.org, une activité avec d’autres cartes spéciales (cartes à points) permet de passer de l’écriture binaire d’un nombre à son écriture décimale et vice-versa. Il est aussi proposé d’énumérer les nombres à l’aide de ces cartes, c’est-à-dire de déterminer le successeur d’un nombre représenté en binaire. Cathy Louvier et Nathalie Revol dans une classe de CM1, à l’école Guilloux de St-Genis-Laval12, proposent plusieurs activités pour le primaire inspirées des activités du site http://csunplugged.org. Elles présentent rapidement l’activité proposée dans cet article sous la forme du tour de magie. Pour aller encore plus loin, dans le mensuel « Pour la Science » de juillet 2014, pp. 76-8113, Jean-Paul Delahaye propose « Un tour de cartes mathématique ». Ce tour de cartes utilise des cartes à jouer traditionnelles. Il est plus complexe et utilise des notions de graphes rouges et noirs. Ce tour est aussi présenté par Michel Rigo sur le site Images des Maths14.
Contributions
Nous décrivons en détail le fonctionnement du tour de magie, puis nous donnons un retour d’expérience du déroulement de l’activité au collège. Ensuite, nous présentons une fiche permettant de convertir un nombre décimal en binaire. Afin de permettre aux élèves de pratiquer cette conversion, nous suggérons de leur faire faire des dessins-mystères binaires. Enfin, nous proposons d’aller plus loin en utilisant des cartes à points pour apprendre les quatre opérations élémentaires du calcul en notation binaire. La principale différence par rapport au décimal est que les tables de multiplication et la comparaison de deux nombres sont immédiates en binaire.
Plan
La section 2 est consacrée au tour de magie. La section 3 décrit deux algorithmes de conversion d’un nombre entier entre la base 10 et la base 2. Enfin, dans la dernière section, nous décrivons des activités sur les opérations arithmétiques élémentaires en binaire.
Tour de magie
Les différentes étapes du tour de magie sont présentées ci-après, ainsi que son fonctionnement. Ensuite, deux paragraphes sont consacrés à un compte rendu d’expérimentation en classe, puis à une courte analyse.
Déroulement du tour
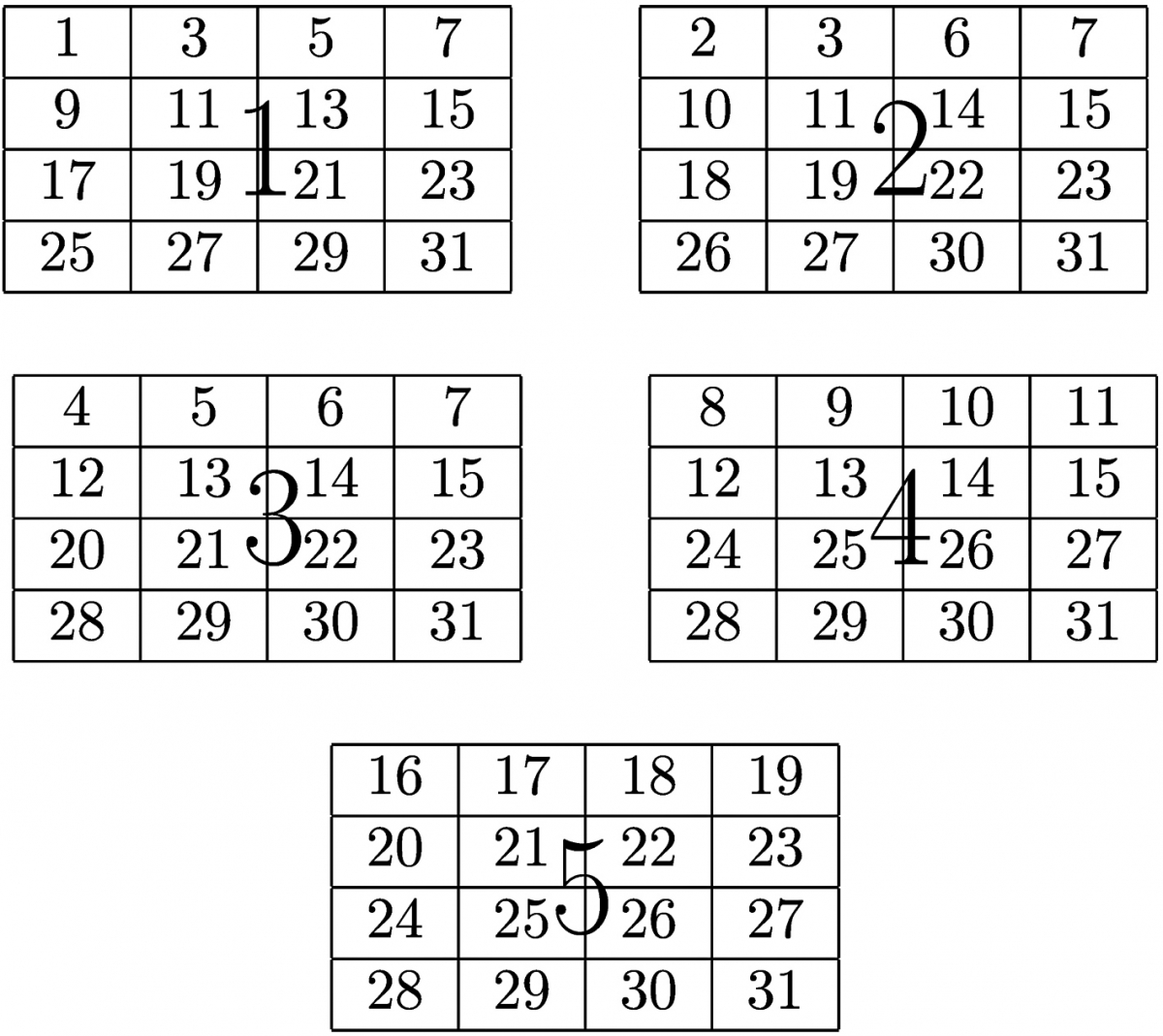
Le magicien (l’enseignant) demande à un spectateur (un élève) de choisir secrètement un nombre entre 0 et 31. En posant cinq questions, le magicien découvre le nombre secret. Pour cela, il dispose des cinq cartes de la figure 1. Ces cartes comportent chacune seize cases contenant les nombres indiqués.
Le magicien montre les cartes une par une (dans l’ordre) au spectateur. Chaque fois, il demande si le nombre secret est présent ou non sur la carte. Une fois qu’il a obtenu la réponse aux cinq questions, le magicien trouve le nombre choisi par le spectateur.
Fonctionnement du tour
Le magicien mémorise les cartes pour lesquelles le spectateur a répondu que le nombre secret est présent. Si par exemple, il s’agit des cartes 1, 3 et 4, alors ce nombre est $13 = 1 + 4 + 8$. Les termes de la somme sont les premiers nombres (en haut à gauche) de chaque carte pour laquelle le spectateur a indiqué que son nombre secret était présent. Plus précisément, si le spectateur indique la carte i, alors le magicien mémorise $2^{i - 1}$. Une fois toutes les cartes passées, il suffit de sommer les nombres mémorisés. Ainsi, sur l’exemple précédent, le magicien obtient le nombre secret comme suit :
\begin{align*} 13 = 1 \times 2^0 + 0 \times 2^1 + 1 \times 2^2 + 1 \times 2^3 + 0 \times 2^4 \end{align*}
En effet, les nombres présents sur la carte i sont exactement ceux dont l’écriture binaire présente un 1 en position i (en partant de la droite), ce qui correspond à l’utilisation de $2^{i-1}$ dans la décomposition en somme de puissances de 2. Ainsi, le nombre 13 s’écrit 1101 en binaire. Les cinq cartes permettent de découvrir tous les nombres dont l’écriture binaire utilise au plus cinq chiffres, c’est-à-dire ceux entre 0 et 31.
Retour d’expérience en classe
Cette activité a été expérimentée par l’une des auteurs dans ses classes de 6ème (2 classes en 2013-2014 et 2 classes en 2014-2015). Le collège est situé en zone rurale. Les élèves sont calmes, curieux et aiment travailler autrement et relever des défis. L’activité s’est déroulée sur 2 séances en 1 h 30 environ au total. Le tour de magie a été présenté aux élèves comme dans la section 2.1. Le professeur est le magicien et un élève choisit un nombre secret. Le professeur trouve le nombre. Le tour est réalisé plusieurs fois de suite, avec différents élèves. Dans toutes les classes, cette activité a été bien accueillie et a même suscité de l’enthousiasme. Les élèves sont captivés et impressionnés, et désireux d’apprendre à réaliser eux-mêmes le tour.
La phase de recherche du fonctionnement du tour s’effectue en classe entière. Les élèves ont l’habitude de ce type d’exercices. Ils émettent spontanément différentes hypothèses, avant de venir les tester devant la classe en tentant de reproduire eux-mêmes le tour. Lors de cette phase, dans une classe, des élèves ont émis l’hypothèse que le professeur regardait et mémorisait chacune des cartes retenues puis qu’il était capable de donner le seul nombre apparaissant sur toutes ces cartes. Pour démontrer que cela n’est pas le cas, le tour a été réalisé les yeux bandés (puisque l’ordre des cartes suffit pour retrouver le nombre). Au bout de quelques minutes et de quelques essais, dans toutes les classes, les élèves ont l’idée que le professeur effectue un calcul. Certains élèves, ayant une idée précise, remplacent le magicien afin de tester leur hypothèse. En cas d’échec, un autre élève est invité à essayer, en cas de réussite, un autre essai est proposé au même élève. Après plusieurs tentatives, (environ 20 minutes) un élève réussit à tous les coups à retrouver le nombre choisi. Dans ce cas, le professeur demande à l’élève de décrire à ses camarades comment il procède. Ensuite le professeur reformule à son tour le fonctionnement du tour.
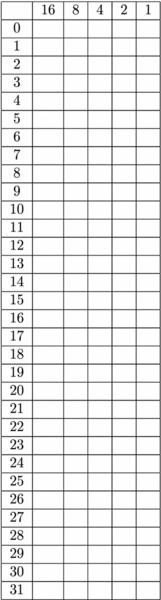
Dans un deuxième temps, le professeur propose de montrer comment construire les cartes magiques. Pour cela, les élèves doivent compléter le tableau de la figure 2. La consigne pour remplir le tableau est de décomposer chaque nombre en somme dont les termes sont 1, 2, 4, 8 et 16. Autrement dit, pour chaque ligne numérotée de 0 à 31, il s’agit de mettre des 1 dans toutes les colonnes dont l’en-tête est utilisé dans la décomposition de ce nombre, et des 0 dans les autres colonnes. Cet exercice est particulièrement adapté pour la classe de 6ème, où beaucoup de décompositions (du type : $231,35 = 231 + 0,3 + 0,05$ ou $231 + 3/10 + 5/100$) sont vues et où le vocabulaire « somme » et « terme » est enseigné. Le professeur donne aux élèves un exemple pour illustrer la consigne. Ce tableau permet de construire la représentation en binaire de tous les nombres entre 0 et 31. Ensuite, pour construire la carte numéro 1, il suffit de recopier dans l’ordre croissant les nombres pour lesquels un 1 est présent dans la dernière colonne du tableau. Il reste alors à procéder de même avec les quatre autres colonnes pour construire les quatre autres cartes.
Le professeur peut faire coller le tableau sur le cahier des élèves avec en titre « Écriture binaire des nombres ». Sous le tableau, les élèves notent que l’écriture des nombres utilisant des 0 et des 1 s’appelle l’écriture en base 2. En remarque, ils notent que l’écriture habituelle est l’écriture en base 10. Puis des exemples sont proposés pour illustrer ces deux notions.
Pendant la recherche ou pendant l’explication, dans toutes les classes, des élèves remarquent que les premiers nombres (en haut à gauche) de chaque carte, qui servent à écrire les décompositions, doublent d’une carte à l’autre. Ainsi il est naturel de demander par quel nombre débuterait la carte suivante : ici la carte numéro 6, qui débuterait donc par $25 = 32$. Il est alors possible de demander aux élèves de construire à la maison les cartes pour pouvoir deviner des nombres entre 0 et 63. Pour préparer ce travail, le professeur peut demander :
- Quel est le premier nombre de la carte numéro 6 ?
- Avec 6 cartes, le tour permettrait de deviner des nombres allant de quel nombre jusqu’à quel nombre ?
- Les nouvelles cartes auront-elles le même nombre de cases que celles utilisées en classe ?
- Combien de cases les nouvelles cartes auront-elles ?
- Comment construire les nouvelles cartes ?
La construction complète des six cartes permettant de deviner des nombres de 0 à 63 est fastidieuse, une seule élève sur les quatre classes a eu le courage de les construire entièrement.
Pour pouvoir réaliser le tour dans leur famille, de nombreux élèves dans chaque classe ont réclamé des photocopies des cartes magiques. Il paraît donc recommandé de prévoir des gabarits de cartes de plus petite taille que celles utilisées en classe, pour limiter le volume de photocopies.
La séance se termine par une phase de mise en commun menée par le professeur. Le lien avec l’informatique est fait à ce moment-là. Le professeur explique que les ordinateurs travaillent en binaire, ce qui signifie que toute information stockée dans un fichier est codée par des 0 et des 1. Ce qui est vrai pour les nombres naturels, comme dans l’activité proposée ici aux élèves, l’est également pour la vidéo, le texte, l’image, le son, en utilisant des règles de représentation de l’information adaptées dans chaque cas.
Analyse
Le fait que l’activité proposée prenne la forme d’un tour de magie est un facteur de motivation pour les élèves. En effet, nous avons observé que, dès le début de la séance, les élèves montrent un grand intérêt pour l’activité. Ils sont dans un premier temps impressionnés (applaudissements). Ensuite, ils veulent connaître le fonctionnement du tour, et ils sont prêts à faire des efforts pour apprendre de nouvelles choses afin de devenir magiciens à leur tour. R. Viau et J. Bouchard dans1 identifient les dimensions de la dynamique motivationnelle d’élèves du secondaire lors d’une activité. Reprenons cette grille de lecture pour analyser les perceptions a priori des élèves pour la tâche proposée ici :
- Valeur : perception qu’a un élève de la valeur de l’activité d’apprentissage. Ici, c’est la perspective valorisante de devenir magicien qui jouerait ce rôle.
- Compétence : la perception qu’il a de sa compétence à l’accomplir. Ici, le fonctionnement du tour est aisément accessible. De plus, l’élève comprend la construction des cartes et est capable (au moins en théorie) de réaliser des cartes pour un tour sur des nombres plus grands. Le sentiment d’efficacité de l’élève dans cette tâche est probablement élevé.
- Contrôlabilité : la perception du degré de contrôle qu’il peut exercer sur le déroulement et sur les conséquences de cette activité. Ici, pouvoir refaire le tour à la maison représente une valorisation que l’élève reconnaît et permet de renforcer cette perception de contrôle.
Un deuxième aspect intéressant de l’activité est l’initiation à la recherche. En effet, elle constitue un défi avec un véritable enjeu, mais qui reste de difficulté raisonnable, ce qui permet à la plupart des élèves d’en venir à bout. La recherche peut être effectuée en classe entière comme proposée précédemment mais peut aussi se faire en groupe selon les habitudes de la classe et du professeur. Il peut être envisagé de prévoir des indices et coups de pouce ainsi que de demander la réalisation d’une affiche résumant la recherche des élèves, ou encore d’un compte rendu de recherche dans un cahier d’expériences. Enfin, lorsque ce type d’activité est une nouveauté pour la classe, cela peut accroître l’attention et la motivation des élèves, mais pas toujours : une des collègues en formation à la MPSA a fait part d’un relatif échec dans une classe de 4e très scolaire et peu habituée à pratiquer des activités de découverte, et donc non notées, où ses élèves n’ont pas beaucoup apprécié d’être sortis de leurs habitudes. Une activité de recherche isolée a plus de risque de déconcerter les élèves.
Pour finir, notons que les cartes magiques utilisées par Cathy Louvier et Nathalie Revol dans une classe de CM1, à l’école Guilloux de St-Genis-Laval pour une activité similaire sont un peu différentes. En effet, les nombres sont écrits en désordre sur chaque carte (et non dans l’ordre croissant). Cela renforce l’effet magique, mais complique la tâche des élèves. C’est pourquoi, pour que la phase de recherche garde une durée raisonnable, et pour éviter de décourager les élèves, il nous semble inutile d’ajouter cette difficulté supplémentaire à l’énigme qui leur est proposée.
Construire la représentation binaire d’un nombre entier naturel écrit en base 10
Nous proposons d’abord deux algorithmes de conversion d’un nombre entier entre la base 10 et la base 2, puis une activité de mise en pratique.
Algorithmes
Pour convertir l’écriture d’un entier naturel de la base 10 vers la base 2, nous proposons deux fiches, mettant en œuvre les deux méthodes classiques :
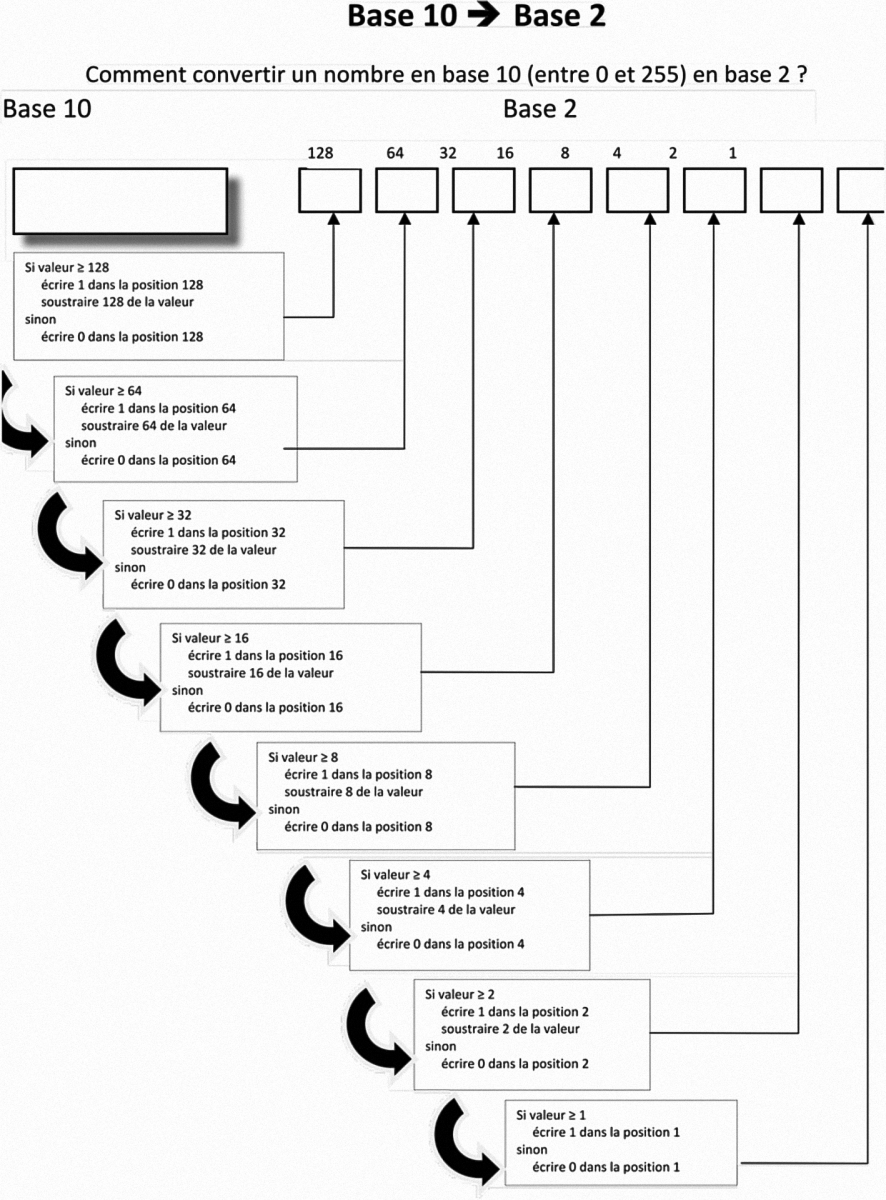
- la première, basée sur des soustractions successives, est présentée dans la figure 3 ;
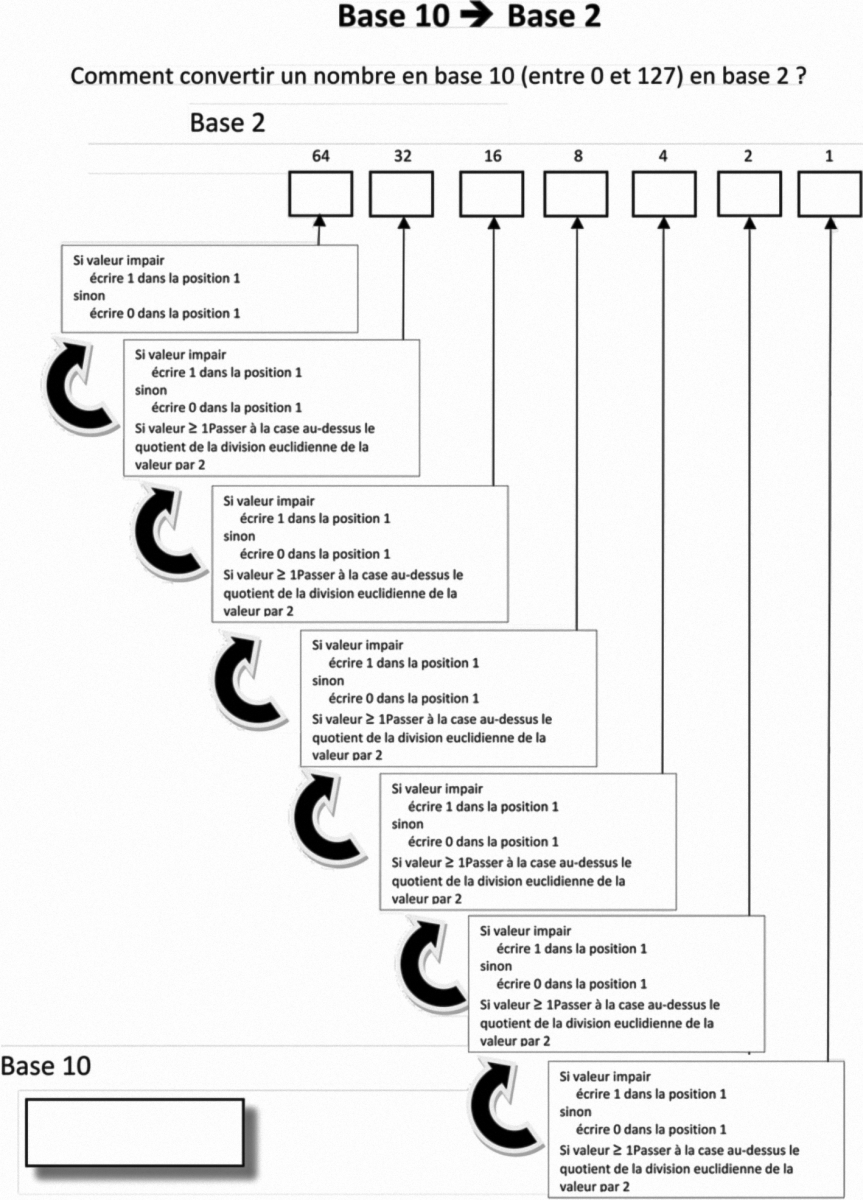
- la seconde, basée sur des divisions euclidiennes par 2, est présentée dans la figure 4.
Il est intéressant de remarquer que la construction du nombre binaire résultat s’effectue de gauche à droite pour la première approche alors qu’elle s’effectue de droite à gauche pour la seconde. Ceci montre clairement que les deux algorithmes sont différents.
Notons que la version basée sur les divisions euclidiennes par 2 peut être utilisée pour travailler ce chapitre en classe de sixième.
Nous décrivons comment ces deux approches fonctionnent sur l’exemple de la conversion du nombre 13 en base 2.
-
Pour la fiche de la figure 3 : le nombre 13 est écrit dans la case en haut à gauche. En effectuant la première ligne, comme 13 est inférieur à 128, il faut écrire 0 dans la position 128 et passer à la ligne suivante en écrivant 13 à côté de la flèche. Des zéros seront ainsi placés sur les positions 64, 32 et 16. Comme 13 est inférieur à 8 il faut écrire 1 dans la position 8 et calculer $13 − 8 = 5$, puis passer la valeur 5 à la ligne suivante en l’écrivant à côté de la flèche. Ensuite 5 étant plus grand que 4, il faut écrire 1 dans la position 4 et passer $5 − 4 = 1$ à la ligne suivante en l’écrivant à côté de la flèche. Ensuite il faut écrire 0 dans la position 2 et écrire 1 à côté de la dernière flèche. Le résultat 00001101 est alors écrit dans les cases 128 à 1. Notons qu’en utilisant cette fiche, des zéros à gauche peuvent apparaître, puisque le calcul des bits se fait de gauche à droite.
- Pour la fiche de la figure 4 : le nombre 13 est écrit dans la case en bas à gauche. Les lignes sont effectuées de bas en haut en suivant les flèches. Pour la première ligne, comme 13 est un nombre impair, il faut écrire 1 dans la position 1. La division euclidienne de 13 par deux donne $13 = 2 \times 6 + 1$, et le quotient 6 est écrit à côté de la flèche pour le passer à la ligne au-dessus. Ensuite, 6 est un nombre pair, donc il faut écrire 0 dans la position 2, et effectuer la division euclidienne $6 = 2 \times 3 + 0$. Le quotient 3 est écrit à côté de la flèche pour passer à la ligne au-dessus. Il reste à écrire 1 dans la case 4 et dans la case 8 en passant respectivement les quotients 1 et 0. Pour la case 16, la valeur est nulle et le processus s’arrête. Le résultat 1101 est alors écrit dans les cases 64 à 1.
Dessins-mystères binaires
Les dessins-mystères binaires (voir figure 5) peuvent être utilisés pour faire pratiquer les conversions décimal-binaire ou bien en guise d’évaluation. Il s’agit de faire remplir une grille où le contenu de chaque ligne est défini par un nombre écrit en base 10 que les élèves doivent convertir en binaire. Ensuite, les 0 sont laissés blancs, et les 1 sont coloriés. Le résultat forme alors un dessin. Il est possible de demander aux élèves de créer leurs propres dessins-mystères binaires en devoir à la maison, puis de l’échanger avec un camarade pour validation des calculs. Il est important d’attirer l’attention des élèves sur la nécessité d’écrire les nombres en binaire sur 6 positions ici (en fonction de la taille de la grille donnée). Par exemple, pour représenter le nombre 2 en binaire correspondant à la ligne A, il faut écrire 000010.
Opérations en binaire
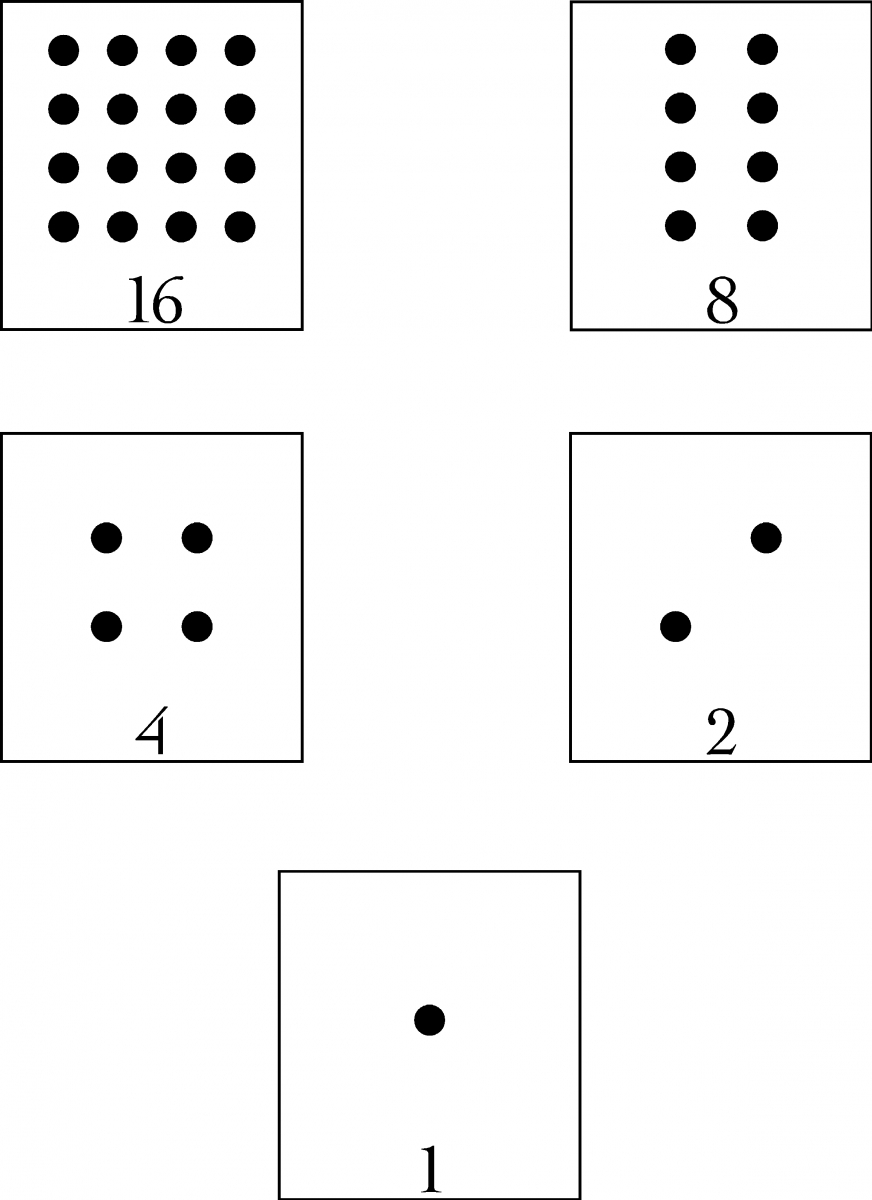
Après l’introduction de la représentation des nombres en binaire à l’aide du tour de magie, nous présentons des activités permettant de manipuler cette écriture. Elles permettent en premier lieu de prolonger l’activité précédente et de consolider la notion de représentation binaire des nombres qui vient d’être introduite. De plus, la comparaison des opérations arithmétiques en décimal et en binaire peut aider à mettre en évidence les algorithmes sous-jacents, qui sont identiques, et surtout leur signification. Nous commençons par des opérations qui sont immédiates en base 2. Ensuite, nous nous intéressons aux quatre opérations arithmétiques : addition, multiplication, soustraction et division. Nous regardons ce que deviennent les algorithmes usuels lorsque les nombres sont écrits en binaire. Dans le cas de l’addition et de la soustraction, nous utilisons les cartes binaires à points reproduites sur la figure 6 pour matérialiser les étapes de l’algorithme. Dans la suite, pour éviter la confusion entre la base 2 et la base 10, nous notons $=_{2}$ les égalités binaires.
Dans l’article1, une analyse didactique d’une activité utilisant les cartes à points binaires est présentée. Nous résumons rapidement ci-dessous cette activité, issue du site « Computer Science Unplugged »2. Les cartes permettent d’afficher un nombre en binaire. Par exemple le nombre $13 = 8 + 4 + 1$ s’écrit en binaire 1101 et est représenté en montrant les cartes à 8, 4 et 1 points et en cachant les cartes à 16 et 2 points comme suit :
Ces cartes sont utilisées pour énumérer les nombres binaires, comme expliqué ci-dessous. Elles se distinguent d’un autre type de cartes à points parfois utilisées dans l’apprentissage de la numération1, car elles représentent le poids de la position et non le nombre lui-même. Ainsi, la troisième carte de l’exemple précédent indique que le poids de cette position est de 4. C’est le nombre total de points visibles qui correspond à la valeur du nombre représenté.
Devant la classe, cinq élèves alignés portent chacun une carte. La carte 16 est portée par l’élève de gauche (vu de la classe), et les autres cartes sont dans l’ordre décroissant. Au début, toutes les cartes sont face cachée pour écrire zéro. Pour écrire un, l’élève portant la carte 1 la montre, les autres ne bougent pas. Pour écrire deux, la carte 1 est cachée, la carte 2 montrée, les autres ne changent pas, etc. Sur Internet, il existe des vidéos montrant l’énumération des nombres de 0 à 31 avec cinq élèves2.
Opérations simples
Nous commençons par trois observations simples permettant de faire découvrir aux élèves des propriétés et des opérations immédiates sur l’écriture binaire des nombres.
Tout d’abord, notons que l’écriture en base 2 d’un nombre permet de savoir s’il est pair. Pour cela, il suffit de regarder si le chiffre des unités est un 0. Les élèves peuvent l’observer sur le tableau de la figure 2 et s’en convaincre par la manipulation des cartes à points en :
- remarquant que la carte ne contenant qu’un point n’est jamais présente dans les nombres pairs et que toutes les autres cartes contiennent un nombre pair de points.
- calculant le successeur d’un nombre pair et d’un nombre impair. En supposant qu’un nombre pair se termine toujours par un zéro (n’utilise pas la carte à un seul point), alors son successeur, qui est un nombre impair, utilise la carte à un seul point. Inversement le successeur d’un nombre impair (utilisant la carte à un seul point) n’utilise plus la carte à un seul point (se termine par un zéro) car $1 + 1 =_{2} 10$.
Ensuite, remarquons que la multiplication par 2 d’un nombre écrit en binaire consiste à ajouter un zéro à droite à son écriture. Par exemple, le double de 101 (cinq) est 1010 (dix). De même, la division entière par 2 consiste à retirer le chiffre des unités, qui est, en l’occurrence, le reste de la division et vaut soit 1, soit 0. Cette fois encore, ces propriétés peuvent apparaître en observant le tableau de la figure 2 ou en manipulant les cartes à points. Les opérations de multiplication et de division par 2 pour des nombres représentés en binaire sont similaires à la multiplication et à la division par 10 pour la représentation décimale des nombres, opérations dont les élèves oublient rapidement le sens. Ces notions sont travaillées en 6ème et le professeur peut prévoir un prolongement de l’activité avec les cartes magiques. Une mise en parallèle des opérations en binaire et en base 10 peut aider les élèves à s’approprier la signification des modes opératoires, qui sont identiques.
Enfin, la comparaison de deux nombres en binaire ayant le même nombre de chiffres (quitte à compléter à gauche par des zéros le nombre le plus court) consiste à trouver le nombre ayant le premier zéro à partir de la gauche : c’est le plus petit. Le professeur fait observer que le processus de comparaison est semblable à celui en base 10, il est seulement un peu plus simple car il suffit juste de savoir que 1 est supérieur à 0, au lieu d’avoir besoin de connaître l’ordre de tous les chiffres de 0 à 9.
Addition
Les tables d’additions en base deux sont courtes car :
- ajouter 0 à un nombre b donne ce nombre b ($0 + 1 = 1 + 0 = 1$ et $0 + 0 = 0$)
- ajouter 1 à 1 donne 10.
Afin de montrer le fonctionnement de l’addition, dans la figure 7 nous additionnons les nombres 1101 (13) et 111 (7), et le résultat est 10100 (20).
Pour matérialiser cette addition à l’aide des cartes à points, nous recommandons d’en utiliser quatre jeux :
- deux pour représenter les opérandes ;
- un pour représenter le résultat ;
- un pour représenter les retenues1.
Le premier jeu de cartes représentant le nombre treize est disposé de telle sorte que les cartes sont rangées dans l’ordre décroissant et les cartes 8, 4 et 1 sont faces visibles et les autres cartes sont faces cachées. En dessous, le second jeu de cartes est aligné selon le même principe pour représenter le nombre sept. La ligne du résultat est placée sous la ligne du nombre sept et toutes les cartes sont faces cachées. Le dernier jeu servant aux retenues est disposé au-dessus de la ligne du treize et toutes les cartes sont faces cachées.
L’addition est effectuée en utilisant l’algorithme habituel en partant de la droite vers la gauche. Sur l’exemple, l’addition commence par $1 + 1 =_{2} 10$ « je pose 0 et je retiens 1 », pour les cartes cela correspond à $1 + 1 = 2 = 2 + 0$ : la carte des unités de la ligne résultat n’est pas retournée et la carte des « deuzaines » de la ligne des retenues est retournée. Ensuite, pour la colonne suivante, nous avons $1 + 0 + 1 =_{2} 10$ ce qui correspond avec les cartes $2 + 0 + 2 = 4 = 4 + 0$ : la carte des deuzaines de la ligne du résultat n’est pas retournée et la carte des quatraines de la ligne des retenues est retournée. Puis $1 + 1 + 1 =_{2} 11$ correspond sur les cartes à $4 + 4 + 4 = 12 = 8 + 4$, la carte des quatraines de la ligne du résultat et la carte des huitaines de la ligne des retenues sont toutes les deux retournées. Le même procédé est répété pour les colonnes restantes. Sur la ligne du résultat les cartes retournées sont les cartes 16 et 4 soit 20 qui est bien la somme de 13 et 7. Comme en décimal, il est possible que le résultat comporte un chiffre de plus que les opérandes, il faudrait alors utiliser la carte représentant la puissance de 2 supérieure (ici 32).
L’intérêt d’utiliser les cartes à points est que la valeur de la retenue est explicite, ce qui permet de revenir, par exemple dans un cadre de remédiation, sur le sens propre de la retenue au-delà de la technique opératoire.
Multiplication
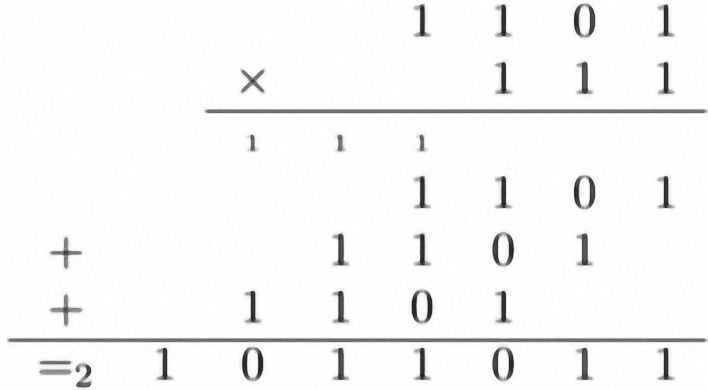
Comme dans le cas de l’addition, les tables de multiplications en binaire sont très courtes, car il suffit de retenir que zéro fois un nombre donne zéro et qu’une fois un nombre donne ce nombre. Les élèves peuvent s’entrainer à utiliser l’algorithme usuel de multiplication à l’aide d’additions sans être gênés par la (mé)connaissance des tables de multiplication.
Pour illustrer la multiplication en base 2, dans la figure 8, nous reprenons les nombres 1101 (13) et 111 (7) utilisés pour l’addition. La représentation de la multiplication à l’aide de cartes à points nécessiterait beaucoup de jeux de cartes, et des cartes comportant beaucoup de points : jusqu’à 10 jeux de cartes, certains comportant des cartes jusqu’à 512 points, par exemple, pour représenter $31 \times 31 = 961$, ce qui correspond en binaire à $11111 \times 11111 =_{2} 1111000001$. Il est donc clairement plus simple d’écrire les nombres avec des 0 et de 1 plutôt que d’utiliser les cartes à points. En l’occurrence, la comparaison des multiplications en binaire et en décimal sur la figure 9 peut aussi servir à illustrer l’intérêt de la représentation des nombres en base 10 — et donc des tables de multiplication — pour les besoins des humains !
Soustraction
Pour effectuer une soustraction en binaire en utilisant l’algorithme habituel, nous pouvons nous aider des cartes à points. Pour cela, nous disposons les cartes représentant les opérandes comme pour l’addition, puis nous ajoutons cette fois-ci une ligne de cartes pour les retenues au-dessus du premier nombre et une seconde ligne de retenues au-dessous du second nombre et finalement une ligne pour le résultat tout en bas. Sur la ligne de retenues d’en haut la carte des unités n’est pas utilisée et les autres cartes sont décalées d’une colonne vers la droite.
Nous illustrons le mécanisme de la soustraction en soustrayant 111 (7) à 1101 (13) dans la figure 10. Dans la colonne des unités, $1 − 1 =_{2} 0$ : la carte des unités du résultat n’est pas retournée ni les cartes des retenues de cette colonne. Ensuite, dans la colonne des deuzaines, il n’est pas possible de faire $0 − 1$, il faut donc utiliser les retenues. Une retenue est ajoutée en haut de la colonne des deuzaines et une retenue est aussi ajoutée en bas dans la colonne des quatraines. En retournant les cartes correspondantes, il apparaît que ces retenues s’équilibrent. Dans la colonne des deuzaines, il est maintenant possible de faire $10 − 1 =_{2} 1$, soit $4 − 2 = 2$ avec les cartes. Dans la colonne des quatraines, il faut effectuer l’opération $1 − 10$ qui est impossible. Il faut donc comme précédemment ajouter une retenue en haut dans la colonne des quatraines et une retenue en bas dans la colonne des huitaines. Dans la colonne des quatraines, l’opération 15 est maintenant $11 − 10 =_{2} 1$ ce qui correspond avec les cartes $12 − 8 = 4$ : la carte des quatraines de la ligne du résultat est retournée. Le même procédé est utilisé pour le reste de l’opération. Le résultat obtenu est $4 + 2 = 6$, ce qui est la différence de 13 et 7.
La notion de retenue pour les soustractions est plus difficile que dans le cas de l’addition ; le fait de rendre les valeurs des retenues explicites peut faciliter la compréhension de la technique opératoire de la soustraction en base 10.
Division
L’utilisation des cartes à points pour cette opération serait particulièrement fastidieuse. Cependant, remarquons que la division euclidienne par l’algorithme usuel à partir de l’écriture binaire des nombres est considérablement épurée par rapport au cas où l’écriture décimale est utilisée. En effet, les tables de multiplication en base 2 sont élémentaires, et la comparaison de deux nombres aussi.
Pour choisir le prochain chiffre du quotient, il suffit de regarder si la partie du dividende considérée est plus petite (choisir 0) ou plus grande (choisir 1) que le diviseur : une étape difficile de ce calcul dans le cas de la base 10 est ainsi évitée. Un exemple est donné dans la figure 10 pour la division de 11010 (26) par 111 (7).
Conclusion
La première rencontre avec la représentation binaire des nombres peut constituer un réel obstacle pour les élèves. Dans cet article, nous avons choisi de proposer plusieurs activités afin d’éviter cet écueil. Nous proposons d’abord un tour de magie pour introduire la représentation binaire des nombres entiers. Ce tour spectaculaire est accessible aux élèves maîtrisant un peu de calcul mental. Les élèves peuvent ensuite reproduire le tour en dehors du contexte scolaire. Une fois cette notion acquise, nous donnons une activité de conversion permettant de passer d’un nombre écrit en base 10 à ce même nombre écrit en base 2. Nous proposons alors des dessins-mystères binaires pour que les élèves pratiquent cette conversion. Enfin, nous proposons de faire (re-)découvrir aux élèves les opérations arithmétiques élémentaires directement en binaire.
Ces activités permettent une première approche des concepts fondamentaux suivants :
- a) la base utilisée pour la construction du système binaire,
- b) la valeur (le poids) de chaque chiffre, en fonction de sa position,
- c) la procédure de conversion du décimal au binaire, et
- d) les règles de base qui gouvernent les opérations arithmétiques à la fois dans le système décimal et dans le système binaire.
Le passage par le jeu est un détour jugé approprié à l’âge des élèves pour cet apprentissage.
Les activités du tour de magie et des dessins-mystères binaires ont été expérimentées dans plusieurs classes, mais elles n’ont pas été suivies d’évaluations de l’apprentissage de la représentation binaire des nombres. La mise en place d’un cadre d’expérimentation rigoureux de ces activités constitue une piste pour des travaux futurs.
Dans le cadre du groupe « Faire de l’informatique sans ordinateur à l’école et au collège » de l’IREM de Clermont-Ferrand, nous proposons d’autres activités qui permettent de découvrir des concepts variés de la science informatique concernant la représentation et le traitement de l’information, l’algorithmique ou la modélisation. Par exemple le code correcteur d’erreurs appelé code de double parité est introduit grâce à un autre tour de magie utilisant cette fois des cartes magnétiques réversibles colorées.