Le théorème d'échantillonnage, souvent appelé théorème de Shannon, constitue une des bases du domaine du traitement de l'information. Mais Shannon lui-même ne s'en attribue pas le mérite et effectivement, on le retrouve sous une forme ou une autre dans de nombreux travaux antérieurs. Cet article nous permet de remonter le temps aux sources de ce théorème, aussi bien chez les ingénieurs que les mathématiciens.
Le fameux « théorème d'échantillonnage de Shannon » stipule qu'un signal — une fonction du temps $f(t)$ — à « bande limitée » peut être parfaitement reconstruit à partir de ses « échantillons » $f(k)$ (où $k$ est entier) par interpolation à l'aide de sinus cardinaux : $$ f(t)=\sum_{k\in\mathbb{Z}} f(k) \operatorname{sinc} (t-k) $$ La notation $\operatorname{sinc}$ désigne ici le sinus cardinal 1, défini par : $$ \operatorname{sinc} t= \frac{\operatorname{sin} \pi t}{\pi t}. $$ Son graphe est donné ci-dessous.
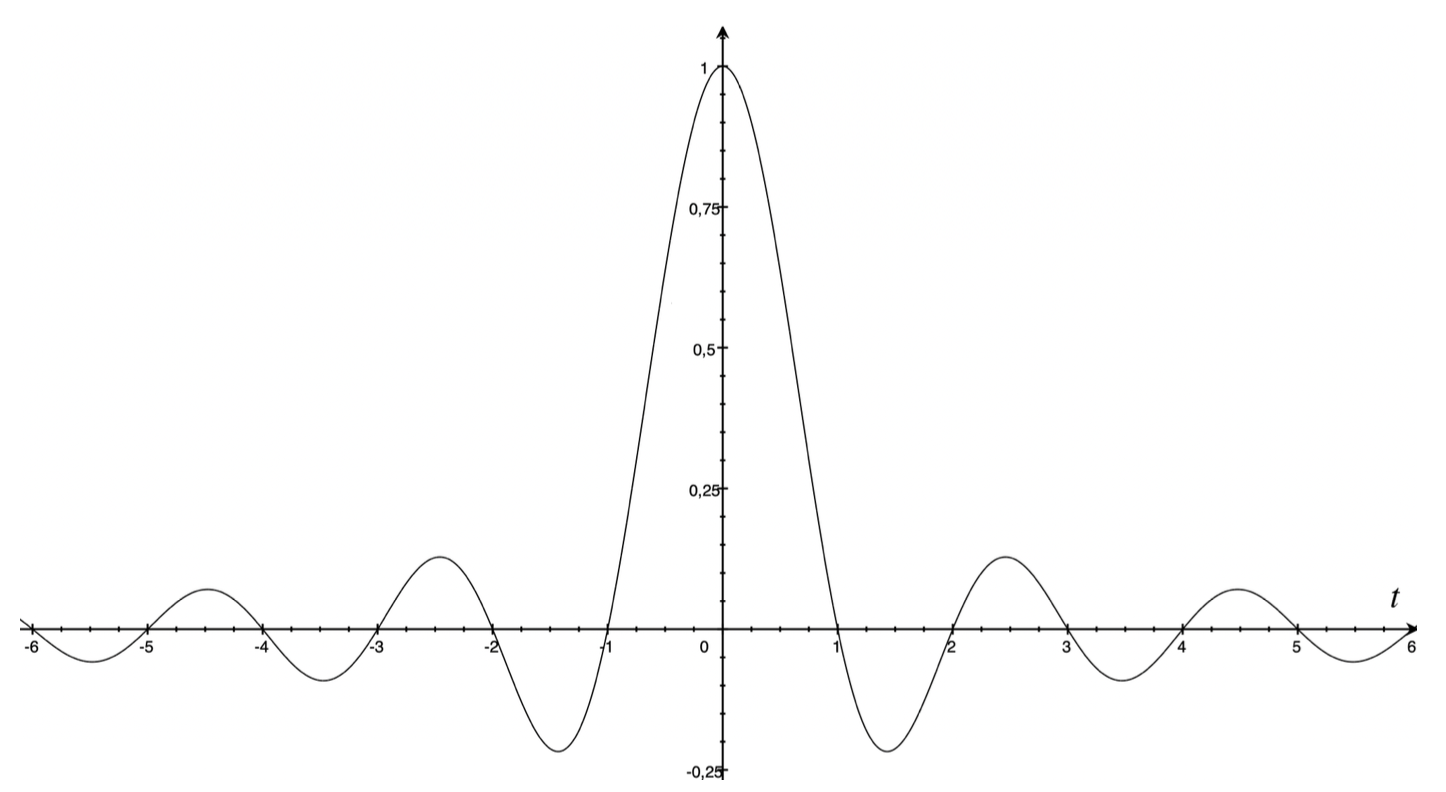
Graphe du sinus cardinal, qui s'annule en tout point entier non nul.
Le sinus cardinal est une bonne fonction d'interpolation puisque ses propres « échantillons » sont tous nuls sauf2 celui en $0$ : $$ \operatorname{sinc} k = \left\{ \begin{array}{ll} 1 & \text{si $k=0$,}\\ 0 &\text{sinon.} \end{array}\right. $$ Cette propriété permet de reconstruire le signal par interpolation, comme pour l'illustre la figure suivante :
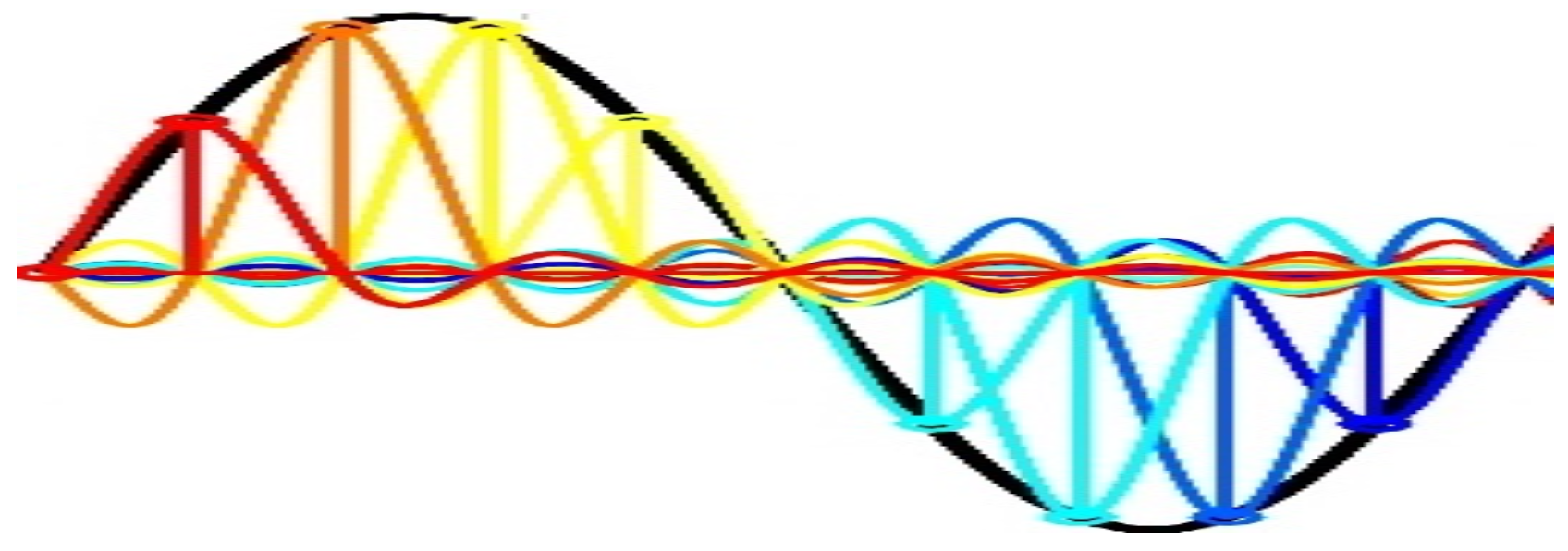
Une reconstruction d'une période d'un cosinus par interpolation à l'aide de sinus cardinaux. Les différentes courbes en couleur s'ajoutent pour reconstruire la courbe en noir.
Dans le théorème, la condition que la signal $f(t)$ soit « à bande limitée » est essentielle : Cela signifie ici que sa transformée de Fourier (voir encadré) $$ \hat{f}(x) = \int_{-\infty}^{+\infty} f(t) e^{-2i\pi x t} \operatorname{dt} $$ où $x$ est un paramètre de fréquence, s'annule pour $|x|\geq 1/2$. Autrement dit, le support fréquentiel du signal (les valeurs non nulles de $\hat{f}$) se trouve dans l'intervalle ouvert centré de longueur $1$.
Notations pour la transformée de Fourier
Il existe plusieurs notations voisines mais différentes pour la transformée de Fourier. La notation courante des mathématiciens est $$ \hat{f}(\omega) = \int_{-\infty}^{+\infty} f(t) e^{-i\omega t} \operatorname{dt} $$ où $\omega$ est une fréquence angulaire, aussi appelée pulsation. Il y a quelques variantes : parfois, on ne met pas le signe moins « $-$ » dans l'exponentielle; parfois aussi, on y inclut une constante multiplicative $\frac{1}{\sqrt{2\pi}}$, qui permet d'avoir une formule d'inversion plus symétrique. On utilise ici une notation différente, courante chez les ingénieurs : $$ \hat{f}(x) = \int_{-\infty}^{+\infty} f(t) e^{-2i\pi x t} \operatorname{dt} $$ où $x=\frac{\omega}{2\pi}$ est un paramètre de fréquence (exprimée en Hertz). Cette notation a l'avantage non seulement d'utiliser un paramètre « physique » de fréquence, mais aussi de simplifier beaucoup de formules impliquant la transformée de Fourier en évitant d'écrire certaines constantes multiplicatives3. Dire que ces deux notations sont respectivement celles des « mathématiciens » ou des « ingénieurs » n'est qu'une convention. Laurent Schwartz, mathématicien réputé qui apporta beaucoup sur la transformée de Fourier dans sa théorie des distributions, employait la « notation des ingénieurs »; alors que Claude Shannon, fondateur de la théorie de l'information qui a eu un impact très important dans les sciences de l'ingénieur, utilisait la « notation des mathématiciens ».
Par une simple homothétie (changement de variable $t\leftrightarrow t/T$) il est facile de donner un énoncé plus général du théorème d'échantillonnage : on peut reconstruire parfaitement un signal $f(t)$ à partir de ses échantillons $f(kT)$ ($k$ entier) à la cadence $1/T$ par interpolation : $$ f(t)=\sum_{k\in\mathbb{Z}} f(kT) \frac{\operatorname{sin} \pi (t/T-k)}{ \pi (t/T-k)} =\sum_{k\in\mathbb{Z}} f(kT)\operatorname{sinc} \bigl(\frac{t}{T}-k\bigr) $$ pourvu que ce signal soit de largeur de bande inférieure à $\frac{1}{2T}$, c'est-à-dire $\hat{f}(x)=0$ pour tout $|x|\geq \frac{1}{2T}$. Cette dernière contrainte de bande limitée se comprend intuitivement : pour qu'on puisse reconstruire la fonction $f$ par interpolation à partir des sinus cardinaux oscillant à la fréquence4 $\frac{1}{2T}$, il ne faut pas que cette fonction puisse osciller plus rapidement encore !
Sans doute la démonstration la plus moderne et radicale du théorème d'échantillonnage utilise le cadre de la transformée de Fourier des distributions tempérées de Laurent Schwartz. Elle est basée sur le fait que la distribution $\sum_{k\in\mathbb{Z}} \delta(t-k)$, appelée peigne de Dirac, est égale à sa transformée de Fourier (une façon moderne d'introduire la formule de Poisson). Ce type d'approche a été exposé pour la première fois, semble-t-il, dans le livre de Philip Mayne Woodward, Probability and Information Theory with Applications to Radar (Probabilité et théorie de l'information appliqués au radar) en 1953.
On peut, comme on vient de le voir, supposer $T=1$. Considérons la suite des échantillons $f(k)$ ($k$ entier) sous la forme d'un train d'impulsions de Dirac, qui s'écrit comme le produit multiplicatif du signal par le peigne de Dirac : $$ \sum_{k\in\mathbb{Z}} f(k)\delta(t-k) = f(t) \cdot \sum_{k\in\mathbb{Z}} \delta(t-k). $$ Si on prend la transformée de Fourier du membre de droite, le produit multiplicatif devient un produit de convolution des transformées de Fourier : $$ \hat{f} \ast \sum_{k\in\mathbb{Z}} \delta(x-k) = \sum_{k\in\mathbb{Z}} \hat{f}(x-k) $$ qui s'écrit comme la périodisation (de période $1$) du spectre du signal. Mais grâce à la condition de bande limitée : $\hat{f}(x)=0$ pour $|x|\geq 1/2$, les différents motifs spectraux $\hat{f}(x-k) $ translatés par des entiers $k$ ont des supports disjoints : il n'y a pas de « recouvrement spectral » (aliasing en anglais) et donc aucune perte d'information sur le signal, qui est donc entièrement caractérisé par ses échantillons $f(k)$. Pour le reconstruire, il suffit de « filtrer » la bande de fréquence du signal, en multipliant en fréquence par une « porte » en fréquence : $$ \Pi(x) = \left\{\begin{array}{ll} 1 &\text{si $|x|\lt 1/2$}, \\ 0 & \text{sinon,} \end{array}\right. $$ Cela sélectionne bien le motif spectral $\hat{f}(x-0)$ pour $k=0$, qui correspond au spectre « passe-bas » du signal : $$ \hat{f}(x)=\Pi(x) \sum_{k\in\mathbb{Z}} \hat{f}(x-k). $$ Il suffit alors d'appliquer une transformée de Fourier inverse pour retrouver le signal $f(t)$ dans son intégralité. Or, pour la porte $\Pi$, la formule d'inversion de Fourier donne $$ \int \Pi(x) e^{2i\pi xt} \operatorname{dx} = \int_{-1/2}^{+1/2} e^{2i\pi xt} \operatorname{dx} = \bigl[ \frac{e^{2i\pi xt}}{2i\pi t}\bigr]_{-1/2}^{+1/2}=\frac{\operatorname{sin} \pi t}{\pi t} $$ ce qui montre que $\Pi=\widehat{\operatorname{sinc}}$ est la transformée de Fourier du sinus cardinal. Ainsi, en revenant en temps par transformée de Fourier inverse de l'expression $$ \hat{f}(x) =\widehat{\operatorname{sinc}}(x)\cdot \sum_{k\in\mathbb{Z}} \hat{f}(x-k), $$ le produit multiplicatif devient un produit de convolution, et on trouve $$ f(t) = \operatorname{sinc} \ast \sum_{k\in\mathbb{Z}} f(k)\delta(t-k) = \sum_{k\in\mathbb{Z}} f(k)\operatorname{sinc}(t-k) $$ qui est la formule d'interpolation du théorème.
Claude Shannon, 1949
Claude Elwood Shannon est celui qui a rendu le théorème d'interpolation universellement populaire en posant les bases de sa théorie de l'information, dans un article classique Communication in the Presence of Noise (Communication en présence de bruit) publié en 19495.
Voici l'énoncé du théorème :

Le théorème 1 d'échantillonnage... par Shannon (1949). Ici $W$ est la largeur de bande (band Width an anglais), cps signifie cycle per second ou Herz, et avec nos notations précédentes $W=1/2T$ et $T=1/2W$.
Démonstration de Shannon
L'esquisse de démonstration par Shannon utilise les séries de Fourier : en effet, toujours en supposant $T=1$ pour simplifier, le théorème d'inversion de Fourier montre que le signal $f$ est reconstruit à partir de sa transformée de Fourier par la formule $$ f(t)= \int_{-\infty}^{+\infty} \hat{f}(x) e^{2i\pi x t} \operatorname{dx} = \int_{-1/2}^{+1/2} \hat{f}(x) e^{2i\pi x t} \operatorname{dx}. $$ Dans la dernière égalité, on a utilisé le fait que $f$ est bande limitée, plus précisément que le support fréquentiel de $\hat{f}$ se trouve dans l'intervalle ouvert $]\!-\frac{1}{2},\frac{1}{2}[$ centré de longueur $1$. Par conséquent, les échantillons du signal s'écrivent $$ f(k)=\int_{-1/2}^{+1/2} \hat{f}(x) e^{2ik\pi x} \operatorname{dx}, $$ qui sont exactement les coefficients de Fourier de la fonction $\hat{f}(x)$, prolongée par périodicité de période 1 an dehors de l'intervalle $]\!-\frac{1}{2},\frac{1}{2}[$. Shannon en déduit que la transformée de Fourier $\hat{f}$ de $f$, et donc $f$ lui-même, est entièrement déterminée la donnée des échantillons $f(k)$. C'est la série de Fourier correspondant à ces coefficients de Fourier qui permet de reconstruire $\hat{f}$ : $$ \hat{f}(x)=\sum_{k\in\mathbb{Z}} f(k)\,e^{-2ik\pi x} $$ et donc $f$ lui-même, par la formule d'inversion de Fourier : $$ f(t)= \int_{-1/2}^{+1/2} \hat{f}(x) e^{2i\pi x t} \operatorname{dx} = \sum_{k\in\mathbb{Z}} f(k) \int_{-1/2}^{+1/2} e^{2i\pi x(t-k)} \operatorname{dx} = \sum_{k\in\mathbb{Z}} f(k)\operatorname{sinc}(t-k) $$ Dans la dernière égalité, on a trouvé la formule d'interpolation du sinus cardinal grâce au calcul de l'intégrale $$\int_{-1/2}^{+1/2} e^{2i\pi x(t-k)} \operatorname{dx}= \Bigl[ \frac{e^{2i\pi x(t-k)}}{2i\pi (t-k)}\Bigr]_{-1/2}^{+1/2}=\frac{\operatorname{sin} \pi (t-k)}{\pi (t-k)}=\operatorname{sinc}(t-k). $$
Le théorème d'échantillonnage, pour Shannon, n'était qu'un moyen de convertir des signaux à temps continu en signaux à temps discret sans perte d'information, conversion nécessaire pour développer complètement sa théorie mathématique de la communication. À cause du succès immense de cette théorie de l'information de Shannon, le théorème d'échantillonnage est la plupart du temps connu sous le nom de « théorème de Shannon ».
Mais comme l'indique la fameuse loi d'éponymie de Stigler, une découverte scientifique ne porte jamais le nom de son auteur, et le théorème d'échantillonnage ne fait pas exception ! Shannon ne s'en attribue d'ailleurs pas le mérite et indique que :
« This is a fact which is common knowledge in the communication art ». (Ce fait est connu dans l'art de la communication.)
En effet, comme on va le voir, la recherche liée à l'industrie du télégraphe et du téléphone a publié des résultats similaires au 20e siècle.
D'où viens-tu, cardinal?
Shannon lui-même n'utilise pas en 1949 la notation $\operatorname{sinc}$ ni le nom « sinus cardinal », qui sont devenus classiques aujourd'hui. La toute première mention de la notation « $\operatorname{sinc}$ » vient de Philip Mayne Woodward déjà mentionné ci-dessus, dans un article intitulé Information Theory and Inverse Probability in Telecommunication (Théorie de l'information et probabilité inverse en télécommunications), écrit avec I.L. Davies, publié en 1952.

Le théorème d'échantillonnage avec la notation $\operatorname{sinc}$ par Woodward et Davies : « $\operatorname{sinc} x$ est une abréviation pour $\frac{\operatorname{sin}\pi x}{\pi x}$. Cette fonction intervient si souvent en analyse de Fourier et ses applications qu'elle semble mériter une notation à elle. »
Curieusement, Woodward ne précise nullement la signification du « c » dans la notation $\operatorname{sinc}$ et ne donne aucun nom particulier à cette fonction. On peut seulement supposer qu'il s'agit de l'initiale de « cardinal » à cause de la référence à Whittaker (voir ci-dessous) qui utilise la notion de « fonction cardinale » dans ce contexte. La toute première mention du nom « sinus cardinal » que l'on a pu trouver est dans un article du Colonel Jean (Charles) Lochard, ingénieur polytechnicien en radioélectricité, dans son éditorial de l'Onde Électrique — aujourd'hui la revue de l’électricité et de l’électronique (REE) de la société de l'électricité, de l'électronique et des technologies de l'information et de la communication (SEE) — intitulé Introduction et application de certains résultats de l'analyse à la théorie des signaux paru en 1962. Dans cet article, Lochard n'écrit aucune formule (et donc n'emploie pas la notation $\operatorname{sinc}$) mais semble considérer le terme « sinus cardinal » comme bien connu.

Mention du théorème d'échantillonnage avec le nom « sinus cardinal » par Lochard : « la fonction « sinus cardinal » [...] comme chacun sait est la transformée de Fourier d'une fonction égale à une constante quelconque dans un intervalle fini centré sur l'origine, et nulle en dehors de cet intervalle. »
Il semble que le première mention du « sinus cardinal » avec la notation « $\operatorname{sinc}$ » figure dans l'article de 1964 de Gérard Battail Sur l'emploi des signaux a bande limitée dans la théorie des communications.

Utilisation de la notation « $\operatorname{sinc}$ » et du nom sinus cardinal pour désigner la fonction $\frac{\operatorname{sin} x}{x}$ (et non $\frac{\operatorname{sin} \pi x}{\pi x}$) par Battail. Cette différence est due au fait que Battail utilise la transformée de Fourier avec la notation « des mathématiciens » $\hat{f}(\omega) = \int_{-\infty}^{+\infty} f(t) e^{-i\omega t} \operatorname{dt}$.
Jeffrey Weston, 1949
La même année 1949, de l'autre côté de l'Atlantique, l'ingénieur britannique Jeffrey Dennis Weston posa également quelques bases de la théorie de la communication dans son article A Note on the Theory of Communication (Une note sur la théorie de la communication). Il va beaucoup moins loin que Shannon sur la théorie de la communication en se bornant à décrire un système de transmission idéal comme un filtre passe bas et en rappelant que la vitesse de transmission est proportionnel à la largeur de bande. En revanche, il établit mathématiquement le théorème d'échantillonnage de façon plus rigoureuse que Shannon :

Le théorème d'échantillonnage selon Weston.
Démonstration de Weston
Weston considère l'espace $H$ « de Paley-Wiener6 » des fonctions de carré intégrable $f$ dont la transformée de Fourier $\hat{f}$ est à support borné dans $[-1/2,1/2]$. C'est un sous-espace (de Hilbert) de l'espace des fonctions de carré intégrable. L'espace des fonctions $\hat{f}$ admet évidemment comme base orthonormée la base de Fourier des fonctions $e^{-2i\pi k x}$ ($k\in\mathbb{Z}$) définies dans l'intervalle $[-1/2,1/2]$. Par transformée de Fourier inverse : $$ \int_{-1/2}^{+1/2} e^{-2i\pi kx} e^{2i\pi xt} \operatorname{dx}=\operatorname{sinc}(t-k) $$ (même calcul que ci-dessus) qui sont les sinus cardinaux translatés. Par conséquent, le produit scalaire étant préservé, les fonctions $\operatorname{sinc}(t-k)$ constituent une base orthonormée7 de $H$, avec les mêmes coefficients (de Fourier) : $$ \int_{-\infty}^{+\infty} f(t) \operatorname{sinc}(t-k) \operatorname{dt} = \int_{-1/2}^{+1/2} \hat{f}(x) e^{2i\pi kx} = f(k) $$ qui ne sont autres que les échantillons de $f$. Ainsi la formule de reconstruction $$ f(t) = \sum_{k\in\mathbb{Z}} f(k)\operatorname{sinc}(t-k) $$ s'interprète, au sens de la convergence dans l'espace des fonctions de carré intégrable, comme la décomposition de $f\in H$ sur cette base orthonormée des sinus cardinaux.
La contribution de Weston, contrairement à celle de Shannon, est très peu connue. Bien que de formation d'ingénieur, Weston continuera ensuite toute sa carrière en tant que mathématicien pur en topologie et en analyse fonctionnelle.
Isao Someya, 1949
Encore plus loin, au Japon, on connait parfois le théorème d'échantillonnage sous le nom de théorème de Someya : l'ingénieur japonais Isao Someya a en effet publié ce résultat dans son livre 波 形 伝 送 Hakei Densō (Transmission de forme d'onde) indépendamment de Shannon, la même année 1949.

Le théorème 14 d'échantillonnage de Someya. On y reconnait la formule d'échantillonnage (4.14) avec $l=1/T$, $t_0=0$ et la forme explicite correspondant du sinus cardinal en (4.15).
En ces temps difficiles d'après guerre (le Japon faisait partie des vaincus) le laboratoire de télévision de Someya n'avait plus aucun équipement, ses employés étaient réduits à cultiver des champs de légumes dans la cour du laboratoire pour palier la grave pénurie de nourriture, ou à se cantonner à des travaux purement théoriques comme celui de Someya. Il n'y avait aucune publication nationale et les chercheurs japonais n'avaient pas davantage accès à des revues internationales. Heureusement, le travail de Someya a pu être publié sous forme d'un livre juste avant que cette série de publications ne soit abandonnée faute de papier à cause de l'inflation. Il est difficile de savoir si Someya avait été influencé par des travaux antérieurs car il ne cite aucune référence. Il semble qu'il ait abouti au théorème d'échantillonnage de manière totalement indépendante, par une réflexion faite dans un certain isolement sur la nature des signaux « à bande limitée » (sans définition mathématique précise). Son exposé, basé sur la formule sommatoire de Poisson (essentiellement équivalente à celle de Shannon) détaille en longueur les points de vue temporel et fréquentiel.
Dennis Gabor, 1946
Comme exemple de travaux le précédant, Shannon mentionne notamment l'article de Dennis Gabor : Theory of communication (Théorie de la communication) de 1946, qui donne une justification graphique du théorème d'échantillonnage :

Une justification graphique du théorème d'échantillonnage... par Gabor. Le plan temps-fréquence est découpé en « logons » (cellules de Heisenberg) de surface minimale (produit temps-fréquence) $T\cdot W = \frac{1}{2}$ pour un grand nombre $N$ d'échantillons à la fréquence d'échantillonnage $f_s=\frac{1}{T}$, d'où une largeur de bande $W=Nw= \frac{1}{2T}$.
William Bennett, 1941
Sur la justification par le calcul du théorème d'échantillonnage, Gabor se contente en réalité de mentionner l'article de William Ralph Bennett : Time division multiplex systems (Systèmes de multiplexage temporel) de 1941, que Shannon cite également. Gabor, en effet, déclare :
« Bennett has discussed it very thoroughly by an irreproachable method, but, as is often the case with results obtained by Fourier analysis, the physical origin of the results remains somewhat obscure ». (Bennett l'a traité de manière très approfondie par une méthode irréprochable, mais, comme c'est souvent le cas avec les résultats obtenus par analyse de Fourier, l'origine physique des résultats reste quelque peu obscure.)
Voici plus précisément l'énoncé de Bennett : le théorème d'échantillonnage est démontré « en régime permanent » (pour des signaux sinusoïdaux ou périodiques présentant des spectres de raies) :

Le théorème d'échantillonnage... par Bennett pour un signal périodique de fréquence fondamentale $q$ autour de la fréquence nulle $\nu=0$. La condition de non recouvrement spectral revient à une largeur de bande $\omega$.
Hebert Raabe, 1939
L'article de Bennett de 1941 cite à son tour la thèse allemande de Hebert Raabe de 1939, Untersuchungen an der wechselzeitigen Mehrfachübertragung (Multiplexübertragung) (Recherches sur la transmission multiple alternée (transmission multiplex)) qui expose en détail le théorème d'échantillonnage et son application pratique, pour les signaux passe-bas et passe-bande. Son argument est basé sur l'analyse de Fourier du produit du signal par une onde carrée modulante. De ce fait, la fonction interpolante n'est pas exactement le sinus cardinal, et le signal passe-bas échantillonné a une bande de fréquence de largeur légèrement supérieure à $\frac{1}{2T}$. Ce type de considération est nécessaire pour mettre en oeuvre l'échantillonnage d'un signal en pratique.
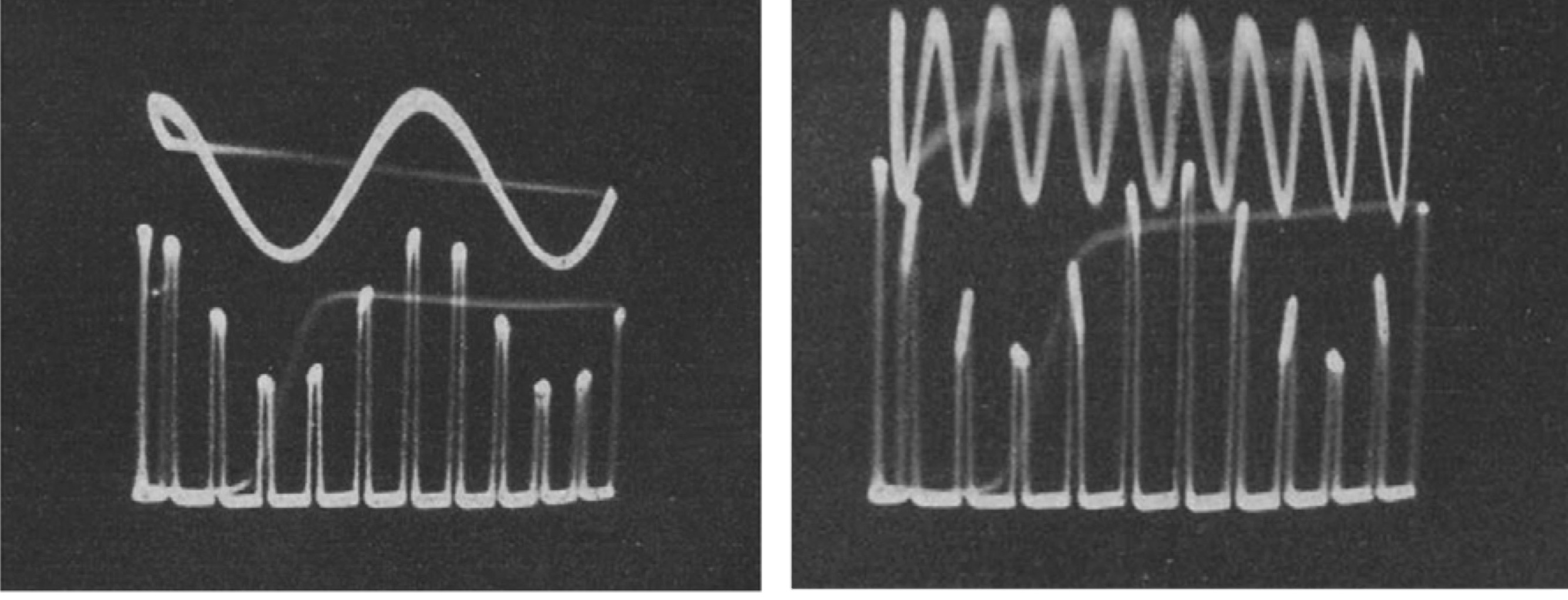
Oscillogrammes des signaux obtenus par Raabe pour justifier le théorème d'échantillonnage. À gauche : une sinusoïde et le résultat de sa multiplication par une onde carrée de fréquence six fois plus élevée (pas de recouvrement spectral) À droite : une sinusoïde de fréquence plus élevée dont le résultat d'échantillonnage est similaire au cas de gauche : il y a eu recouvrement spectral.
La thèse de Raabe, bien que citée par Bennett, est resté méconnue et n'a été redécouverte que dans les années 1980-2000 grâce au travail historique de Hans Dieter Lüke. Raabe y résume ses travaux en écrivant :
Für die dargestellten Übertragungsbedingungen wird die Abtastfrequenz durch den Bereich der Signalfrequenzen bestimmt. Hält man diese unter der Hälfte der Abtastfrequenz, so bleiben alle Rauschfrequenzen oberhalb dieser Grenze und können durch einen Tiefpassfilter vom Empfänger ferngehalten werden. Die Übertragung eines Signals kann also völlig verzerrungsfrei sein, wenn die Abtastfrequenz das Doppelte der höchsten Signalfrequenz beträgt. Die obere Begrenzung der Signalfrequenzen ist also eine wesentliche Bedingung für die verzerrungsfreie Übertragbarkeit im Zeitmultiplexverfahren. (Pour les conditions de transmission présentées, la fréquence d'échantillonnage est déterminée par la plage des fréquences de signal. Si l'on maintient celle-ci en dessous de la moitié de la fréquence d'échantillonnage, toutes les fréquences de bruit restent au-dessus de cette limite et peuvent être maintenues à l'écart du récepteur par un filtre passe-bas. La transmission d'un signal peut donc être totalement exempte de distorsion si la fréquence d'échantillonnage est le double de la fréquence de signal la plus élevée. La limite supérieure des fréquences de signal est donc une condition essentielle pour la transmissibilité sans distorsion en multiplexage temporel.)
Vladimir Kotel'nikov, 1933
Côté russe, l'ingénieur Vladimir Aleksandrovich Kotel'nikov a publié une démonstration complète du théorème d'échantillonnage en 1933 dans son article О пропускной способности ‘эфира’ и проволоки в электросвязи (Sur la capacité de transmission de « l'éther » et du fil dans les électro-communications). Cette publication était destinée à une conférence (première conference de l'Union soviétique sur les questions de communication à Moscou) qui n'a finalement pas eu lieu. Le journal Электричество (Électricité) l'a ensuite rejeté en 1936. À cela s'ajoute que dans les années suivantes, les travaux russes étaient quasiment inaccessibles en Occident. Le travail fondateur de Kotel'nikov est donc resté ignoré en dehors du bloc de l'Est, et n'a été redécouvert internationalement que bien après l'article de Shannon : Mentionné par Andreï Kolmogorov8 dans un article publié aux USA en 1956, le papier original de Kotel'nikov n'a été traduit pour la première fois qu'en 2001.

Page de titre de l'article de Kotel'nikov
Kotel'nikov est apparemment le premier, dans le domaine des télécommunications, à formuler précisément le théorème d'échantillonnage (bien qu'avec une preuve peu rigoureuse mathématiquement). Voici son énoncé, traduit en français (avec $f_1=W$, $\frac{1}{2f_1}=T$) :
Théorème I —- Toute fonction $F(t)$ comprenant des fréquences de $0$ à $f_1$ cycles par seconde peut être représentée par la série : \begin{equation}\tag{1} F(t) =\sum_{-\infty}^{+\infty} D_k \frac{\operatorname{sin} \omega_1 (t-\frac{k}{2f_1}) }{ t-\frac{k}{2f_1}} \end{equation} où $k$ est un entier, $\omega_1=2\pi f_1$, et $D_k$ sont des constantes qui dépendent de $F(t)$. Réciproquement, toute fonction $F(t)$ représentée par la série (1) ne comporte que des fréquences de $0$ à $f_1$. Théorème II —- Toute fonction $F(t)$ comprenant des fréquences de $0$ à $f_1$ peut être transmise continûment, avec une précision arbitraire, au moyen de nombres émis à des intervalles de $\frac{1}{2f_1}$ secondes. En effet, en mesurant la valeur de $F(t)$ aux temps $t=\frac{n}{2f_1}$, où $n$ est entier, on obtient \[ F(\frac{n}{2f_1}) = D_n \omega_1. \] Tous les termes de la série (1) s'annulent pour cette valeur de $t$, sauf le terme avec $k = n$, qui est égal à $D_n \omega_1$. Ainsi, après chaque $\frac{1}{2f_1}$ seconde, nous pouvons déterminer le prochain $D_k$. En transmettant ces $D_k$ successivement après chaque $\frac{1}{2f_1}$ seconde, nous pouvons, selon l'égalité (1), récupérer $F(t)$ à partir d'eux, terme par terme avec n'importe quelle précision.
On voit que Kotel'nikov mentionne aussi une réciproque du théorème d'échantillonnage : non seulement un signal à bande limitée vérifie la formule d'interpolation par les sinus cardinaux, mais réciproquement, une telle formule définit un signal qui est à bande limitée.
Harry Nyquist, 1928
Shannon, à propos du théorème d'échantillonnage, cite également un article célèbre de 1928, Certain topics in telegraph transmission theory (Quelques aspects de la théorie de la transmission télégraphique) de l'ingénieur suédo-américain Harry Nyquist. Ce dernier travaillait, comme Shannon, aux laboratoires Bell, et l'a beaucoup influencé.
Parce que l'article de Nyquist est le plus ancien cité par Shannon à propos du théorème d'échantillonnage, ce théorème est souvent appelé « théorème de Nyquist » ou « théorème de Nyquist-Shannon ». Mais c'est sans doute une erreur historique.
En effet, nulle part dans son article, Nyquist ne considère le problème de l'échantillonnage. Il s'agit plutôt du problème de la transmission « sans distorsion » de symboles (télégraphiques) émis toutes les $T$ secondes sur un canal de bande limitée $W$. Il donne un critère fréquentiel (connu aujourd'hui sous le nom de condition de Nyquist) pour supprimer les interférences entre symboles (ce qu'il appelle distorsions) : la forme idéale du spectre du signal télégraphique doit satisfaire à une certaine condition de symétrie comme illustrée sur la figure suivante :
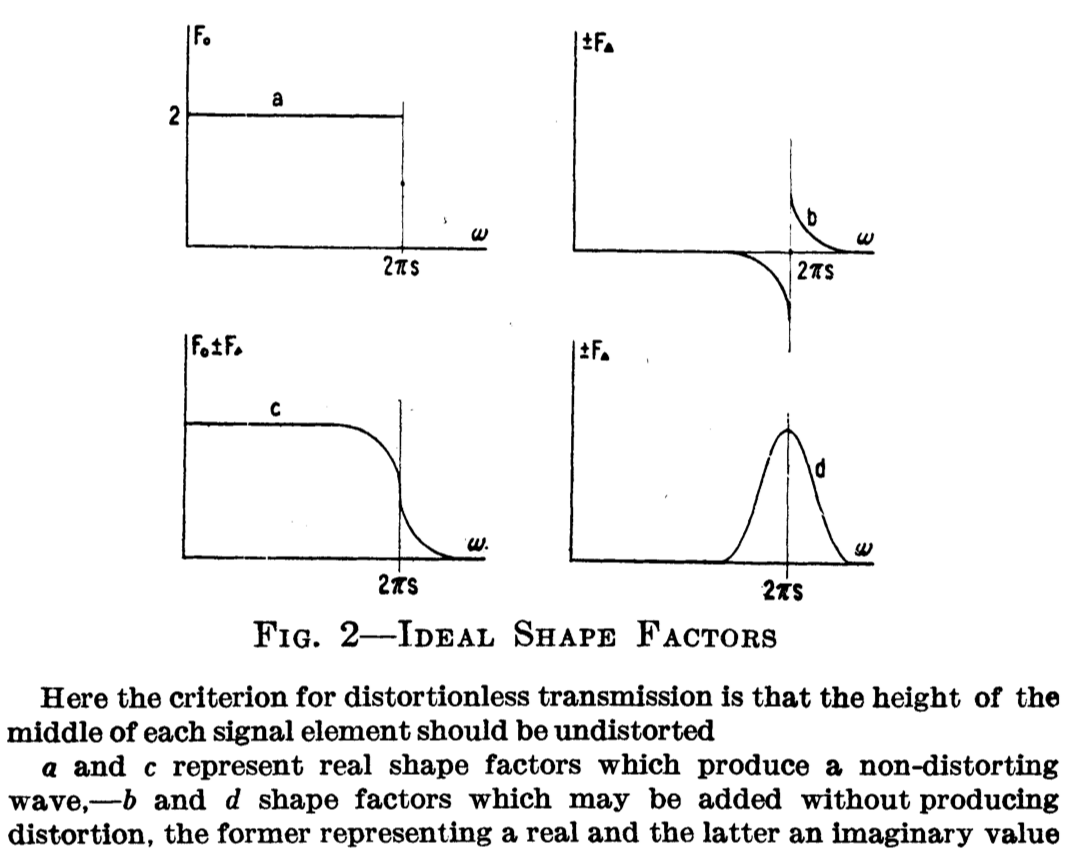
Figure de l'article de Nyquist donnant les « formes idéales » fréquentielles satisfaisant à la « condition de Nyquist » de transmission sans distorsion (sans interférence entre symboles) sur un canal à bande limitée. Ici la fréquence est $\omega/2\pi$ et $s=1/2T$ est la cadence d'émission des symboles complexes (un symbole complexe = deux symboles réels).
Il montre en particulier que la largeur de bande du canal ne doit être pas être inférieure à $\frac{1}{2T}$ (appelée « fréquence de Nyquist ») pour que cela soit possible. Il y a donc une certain similarité mathématique avec le théorème d'échantillonnage où l'on a la relation $W=\frac{1}{2T}$ qui relie bande du signal échantillonné et cadence d'échantillonnage, ce qui explique la confusion. Mais on voit bien que ces deux problèmes (transmission sans interférence et échantillonnage) sont conceptuellement très différents. Ainsi, bien que ce travail de Nyquist est d'une importance fondamentale en transmission numérique, il n'est sans doute pas très loisible d'associer son nom au théorème d'échantillonnage.
Karl Küpfmüller, 1924
Un autre ingénieur contemporain de Nyquist est parfois mentionné comme un des premiers contributeurs du théorème d'échantillonnage : l'allemand Karl Küpfmüller (un des professeurs de Hebert Raabe à Berlin) qui a publié Über Einschwingvorgänge in Wellenfiltern (Sur les phénomènes d'oscillations propres dans les filtres d'ondes) en 1924, et d'autres travaux similaires en 1928 et 1931.

Figure intitulée « Impact de la contrainte du domaine des fréquences » de l'article de Karl Küpfmüller de 1931 écrit en suédois, Utjämningsförlopp inom Telegraf- och Telefontekniken (Oscillations propres (transitoires) dans la technologie du télégraphe et du téléphone). Le temps de mise en vibration est $T=\tau$ et la largeur de bande est $W=f_0$, d'où pour le filtre idéal de réponse indicielle donnée dans la figure (dont la réponse impulsionnelle est le sinus cardinal) la relation $T=\frac{1}{2W}$.
Mais là encore, il ne semble y avoir aucun lien direct avec le problème de l'échantillonnage. Küpfmüller étudie les phénomènes transitoires d'oscillations propres de filtres, en particulier le filtre passe-bas idéal dont les réponse impulsionnelle est le sinus cardinal. Il admet que le temps de mise en vibration totale de régime permanent de ce filtre est donné par la formule $T=\frac{k}{W}$ où $W$ est la sélectivité du filtre, et $k$ est une constante qu'il affirme être au moins égal à $\frac{1}{2}$ (égalité atteinte dans le cas du filtre idéal). Il conclut : « Nous ne pourrons donc jamais descendre en dessous de cette valeur $k=\frac{1}{2}$, quelle que soit l'évolution de la technologie ».
Le relation générale $T\leq \frac{1}{2W}$. ou $W\leq \frac{1}{2T}$, ressemble là encore à la conclusion du théorème d'échantillonnage, bien que le problème étudié soit de nature très différente.

Ainsi, Shannon, en 1949, avait bien raison de préciser que le théorème d'échantillonnage était un fait (plus ou moins bien) connu dans l'art de la communication. Mais Shannon mentionne aussi que le théorème d'échantillonnage était déjà compris comme un théorème d'interpolation par les mathématiciens, avant même son utilisation pour les télécommunications !
Kinnosuke Ogura, 1920
Il est aujourd'hui à peu près certain que c'est le mathématicien japonais {Kinnosuke Ogura} a exposé en 1920 la première démonstration mathématique rigoureuse du théorème d'échantillonnage, dans son article On a certain transcendental integral function in the theory of interpolation (Sur une certaine fonction entière transcendante dans la théorie de l'interpolation).
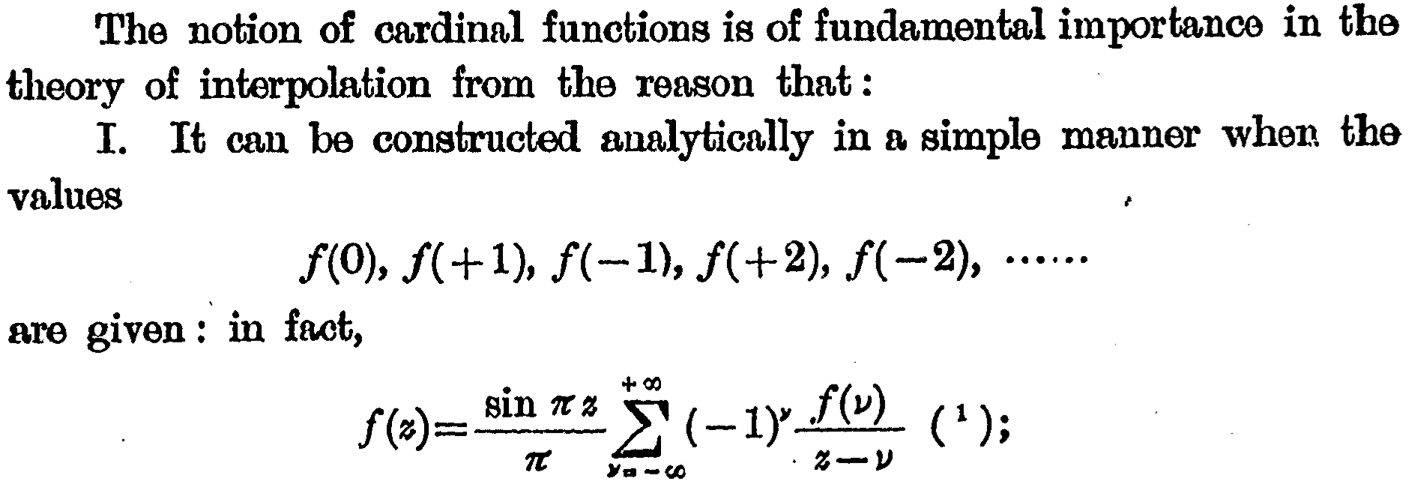
Le théorème d'échantillonnage... par Ogura pour une fonction entière $f(z)$ de la variable complexe $z$. Si on pose $z=t$ réel, alors $(-1)^k \frac{\operatorname{sin} \pi z }{ z-k}=(-1)^k \frac{\operatorname{sin} \pi t }{ t-k}=\frac{\operatorname{sin} \pi (t-k) }{ t-k}=\operatorname{sinc} (t-k)$ de sorte que sa formule se réécrit bien sous la forme usuelle $f(t)=\sum_{k=-\infty}^{+\infty} f(k) \operatorname{sinc}(t-k)$.
Ogura considère que $f$ est une fonction entière de la variable complexe $z$, de type exponentiel $\lt\pi$, c'est-à-dire telle que pour tout $z\in\mathbb{C}$, $$ |f(z)|\leq c \;e^{\sigma |\mathrm{Im}\, z|} $$ pour des constantes $c>0$ et $\sigma\lt\pi$. Il énonce alors que $f$ peut être reconstruite « analytiquement » à partir de ses échantillons $f(k)$ par la formule $$ f(z)=\frac{\operatorname{sin} \pi z}{\pi} \sum_{k\in\mathbb{Z}} (-1)^k \frac{f(k)}{z-k}. $$ À première vue, le lien avec le théorème d'échantillonnage classique n'est pas clair, en particulier en ce qui concerne la condition de bande limitée en fréquence. Mais l'hypothèse que $f$ est une fonction entière de type exponentiel est effectivement naturelle lorsque $f$ est un signal à bande limitée contenue dans l'intervalle $]\!-\frac{1}{2},\frac{1}{2}[$, car $f(z)$ peut être alors représentée par l'intégrale de Fourier $$ f(z)= \int_{-1/2}^{+1/2} \hat{f}(x) e^{-2i\pi x z} \operatorname{dx} $$ qui implique une inégalité du type $|f(z)|\leq c \;e^{\pi |\mathrm{Im}\, z|}$ (la condition d'Ogura est à peine plus restrictive9). Ogura, dans un autre article publié la même année 1920, démontre d'ailleurs la réciproque du théorème d'échantillonnage en montrant qu'une fonction donnée par la formule $\frac{\operatorname{sin} \pi z}{\pi} \sum_{k\in\mathbb{Z}} (-1)^k \frac{f(k)}{z-k}$ est bien représentable par cette intégrale de Fourier, donc à bande limitée. Quant à cette formule, elle se réécrit bien pour $z=t$ réel sous la forme classique : $$ f(t)= \sum_{k\in\mathbb{Z}} \frac{\operatorname{sin} \pi t}{\pi} (-1)^k \frac{f(k)}{t-k} = \sum_{k\in\mathbb{Z}} f(k) \frac{\operatorname{sin} \pi (t-k)}{\pi(t-k)} = \sum_{k\in\mathbb{Z}} f(k) \operatorname{sinc}(t-k). $$
Ogura ne semble pas réaliser l'importance de son résultat; il n'en donne même pas vraiment de démonstration en l'attribuant entièrement à Whittaker, ce qui, comme on va le voir ci-dessous, est contestable. Il se contente de dire qu'une preuve simple et rigoureuse utilise le théorème des résidus à une fonction du type $f(z) \frac{\pi}{\operatorname{sin} \pi z}$ comme décrit dans un manuel d'Ernst Lindelöf sur le calcul des résidus, sans donner plus de détails.
Bien qu'Ogura était un mathématicien reconnu en France (il rencontre Émile Borel à Paris et est invité à la conférence internationale des mathématiciens à Strasbourg en 1920), son œuvre est restée assez ignorée en dehors du Japon où il était surtout connu comme historien et pédagogue. Pour toutes ces raisons, la contribution d'Ogura est restée confidentielle jusqu'à ce qu'elle soit mise en lumière par le travail historique de Paul Leo Butzer et Rudolf Leonhard Stens dans les années 1990.
Démontrons le résultat d'Ogura en appliquant le théorème des résidus, appliqué à la fonction $\frac{f(z)}{t-z}\frac{\pi}{\operatorname{sin}\pi z}$ : $$ \frac{1}{2i\pi}\oint_{\mathcal{C}} \frac{f(z)}{t-z}\frac{\pi}{\operatorname{sin}\pi z} \operatorname{dz} = \sum \text{Rés}\bigl( \frac{f(z)}{t-z}\frac{\pi}{\operatorname{sin}\pi z}\bigr) $$ où la somme porte sur les pôles situés à l'intérieur du cercle $\mathcal{C}$ centré à l'origine contenant $x\in\mathbb{C}$ et des entiers $0,\pm1,\pm2,...$ aussi grands que l'on veut. Le résidu de $\frac{\pi}{\operatorname{sin}\pi z}\sim \frac{1}{z}$ au pôle $z=0$ est $=1$ et puisque $\operatorname{sin} \pi(z-k)=(-1)^k\operatorname{sin} \pi z$, celui en $z=k$ entier est égal à $(-1)^k$. Enfin le résidu de $\frac{f(z)}{t-z}$ en $z=t$ vaut $-f(t)$. On obtient ainsi $$ \frac{1}{2i}\int_{|z|=R}\frac{f(z)}{\operatorname{sin}\pi z} \frac{\operatorname{dz}}{t-z}= \sum_{|k|\lt R} \frac{f(k)}{t-k}(-1)^k - f(t) \frac{\pi}{\operatorname{sin}\pi t} $$ où $R$ est le rayon du cercle. On trouve facilement que $|\operatorname{sin} \pi z|\geq c' \cdot e^{\pi |\mathrm{Im} z|}$ et $|f(z)|\leq c \;e^{\sigma |\mathrm{Im}\, z|}$, l'intégrande est donc uniformément borné et tend vers zéro lorsque $|z|=R\to+\infty$. Par convergence dominée l'intégrale tend vers zéro, d'où la formule voulue.
Edmund Whittaker, 1915
Shannon, mais aussi Watson, en 1949, fait le lien entre les approches des ingénieurs et des mathématiciens, en citant John Macnaghten Whittaker et son livre Interpolatory Function Theory (Théorie des fonctions interpolatoires) de 1935 comme origine mathématique du théorème d'échantillonnage. En réalité, ce livre ne fait que reprendre des travaux antérieurs, et c'est bien Edmund Taylor Whittaker (le père de John Macnaghten) qui en 1915, dans son article On the functions which are represented by the expansions of the interpolation theory (Sur les fonctions qui sont représentées par les formules de la théorie de l'interpolation), a donné l'essentiel du théorème. De ce fait, l'article de 1915 de Whittaker père est rapidement devenu la référence mathématique citée dans la littérature des ingénieurs des années 1950, et le théorème d'échantillonnage est parfois connu sous le nom de « théorème de Whittaker » ou « théorème de Whittaker-Shannon » en référence à Whittaker père.
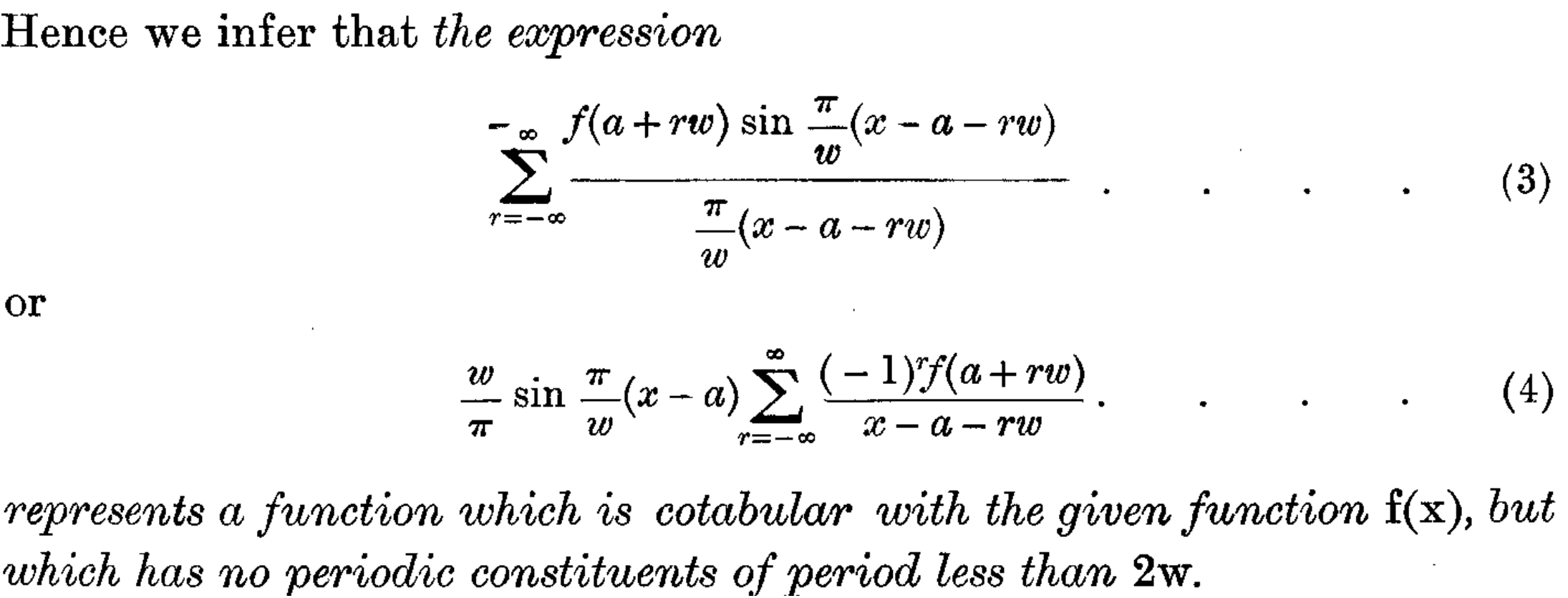
Le théorème d'échantillonnage (ou plutôt d'interpolation) par Whittaker père. Ici $w=T$ est l'intervalle séparant deux « échantillons » consécutifs, et la fonction $f$ résultant de l'interpolation avec des sinus cardinaux (appelée fonction cardinale par Whittaker) « n'a pas de composantes périodiques inférieures à $2w=2T$ », c'est-à-dire de fréquences supérieures à $\frac{1}{2T}$.
À première vue, l'article de Whittaker contient l'intégralité de théorème d'échantillonnage : sa « fonction cardinale » $\sum_{k\in\mathbb{Z}} f(k) \operatorname{sinc}(t-k)$ permet d'interpoler les $f(k)$ par une fonction à bande limitée. C'est la première fois que la notion de limitation fréquentielle est étudiée dans ce cadre.
À y voir de plus près cependant, Whittaker ne démontre pas le théorème d'échantillonnage. Il n'énonce d'ailleurs aucun théorème et se contente d'indiquer quelques intentions parfois assez vagues. En réalité, il s'intéresse plutôt au problème (dual) de l'interpolation des valeurs $f(k)$ par une fonction $f(t)$ dont la solution n'est en général pas unique. Il cherche initialement une solution compatible avec une interpolation polynomiale (nous y reviendrons) puis effectue diverses transformations sur les solutions $f(t)$ pour arriver à sa solution « cardinale » dont il montre qu'elle est analytique et n'admet aucune composante de période inférieure au double de la période des $f(k)$ (par une analyse d'intégrale de Fourier particulière). Whittaker ne mentionne aucun travail antérieur sur le sujet.
Charles-Jean de La Vallée Poussin, 1908
L'idée d'interpolation à l'aide de sinus cardinaux était déjà présent dans un article de 1908 de Charles-Jean de La Vallée Poussin, Sur la convergence des formules d’interpolation entre ordonnées équidistantes. Il utilise bien la « formule d'interpolation fondamentale » qui est celle du théorème d'échantillonnage : $$ \sum_{k\in\mathbb{Z}} f(kT)\operatorname{sinc} \bigl(\frac{t}{T}-k\bigr) $$ mais pour une fonction $f(t)$ à durée limitée, dont le support est dans un intervalle $(a,b)$. Il en résulte la formule d'interpolation n'est qu'approximative et de La Vallée Poussin établit les conditions pour que qu'elle converge vers $f$ lorsque $T\to 0$. Bien qu'aucun lien avec la transformée de Fourier de $f$ n'est établi, on peut en déduire une borne sur l'erreur de repliement de spectre dans le théorème d'échantillonnage due au fait que le signal est à durée limitée (et non à bande limitée).
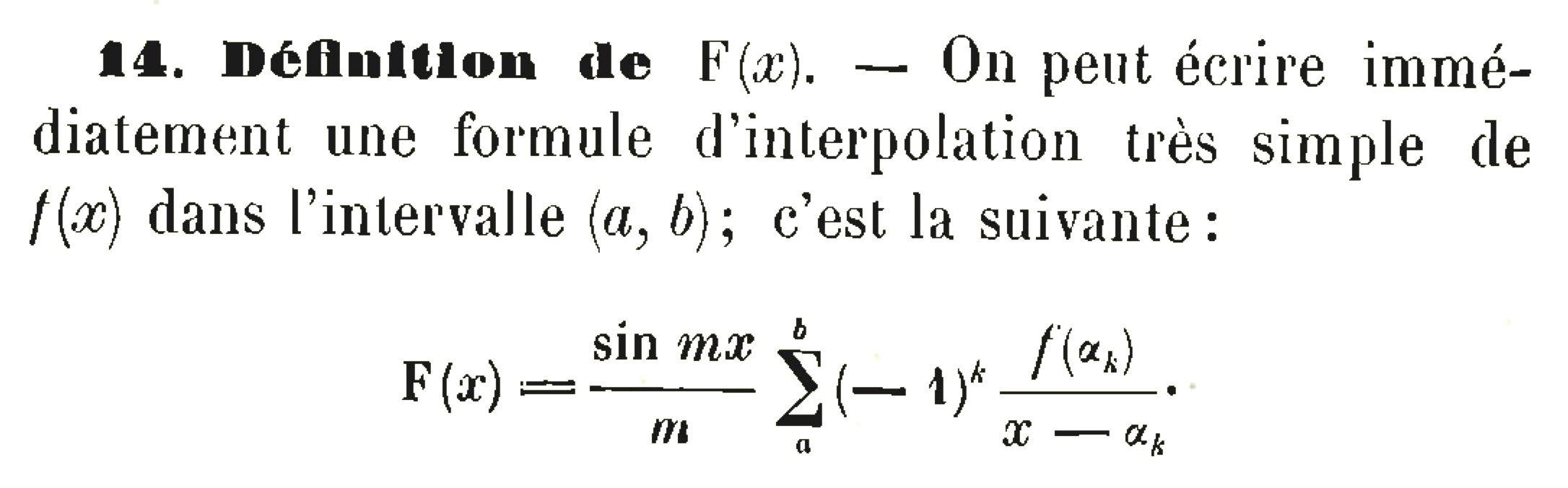
L'interpolation de La Vallée Poussin, où $\alpha_k=\frac{k\pi}{m}$, correspond à la formule d'interpolation du théorème d'échantillonnage pour $m=\pi/T$, où la somme n'est prise que pour les valeurs de $\alpha_k$ comprises entre deux extrémités $a$ et $b$. Si la dérivée de $f$ est à variation bornée, de La Vallée Poussin établit que cette formule tend vers $f$ avec une rapidité de convergence en $\frac{1}{m}$ lorsque $m\to+\infty$.
Comment de La Vallée Poussin est arrivé à cette formule d'interpolation avec les sinus cardinaux sans passer par les propriétés fréquentielles de $f$? Dans son article, après avoir exposé certains défauts de la formule d'interpolation polynomiale de Lagrange, Il explique que « Cette formule n'est pas aussi éloignée de celle de Lagrange qu'elle pourrait le paraître à première vue : elle en est seulement un cas-limite. En effet, que I'on détermine, par la formule de Lagrange, le polynôme qui prend des valeurs données pour des valeurs données de $x$ en progression arithmétique depuis $a$ jusque $b$, et qui s'annule pour toutes les autres valeurs de $x$ appartenant à la même progression et comprises entre $-N$ et $+N$; ce polynôme a pour limite une fonction entière quand $N$ tend vers I'infini; cette limite est notre formule d'interpolation fondamentale. »
Détaillons en le poursuivant le raisonnement de La Vallée Poussin : le polynôme d'interpolation de Lagrange aux points entiers $-N,-N+1,...,N-1,N$ est de la forme : $$ \sum_{k=-N}^N f(k) L_k(t) $$ où $L_k$ est le polynôme de degré $2N$ s'annulant en tous ces points $-N,...,N$ sauf en $k$ où il prend la valeur $L_k(k)=1$. En particulier pour $k=0$ : $$ L_0(t) = \prod_{k=1}^N \bigl(1+\frac{t}{k}\bigr) \prod_{k=1}^N \bigl(1-\frac{t}{k}\bigr) = \prod_{k=1}^N \bigl(1-\frac{t^2}{k^2}\bigr) $$ Faisons $N\to+\infty$. Le polynôme $L_0(t)$ devient un produit infini : $$ \lim_{N\to\infty} L_0(t) = \prod_{k=1}^{+\infty} \bigl(1-\frac{t^2}{k^2}\bigr) =\frac{\operatorname{sin} \pi t }{ \pi t }= \operatorname{sinc} t $$ égal au sinus cardinal par la formule d'Euler des compléments de la fonction $\Gamma$. Puisqu'on interpole à la limite sur tous les entiers, dont l'ensemble est stable par translation, les autres polynômes limites sont simplement les versions translatées $\lim L_k(t)=\lim L_0(t-k)=\operatorname{sinc}(t-k)$, d'où on retrouve la formule d'interpolation du théorème d'échantillonnage : $$ \lim_{N\to\infty}\sum_{k=-N}^N f(k) L_k(t) = \sum_{k\in\mathbb{Z}} f(k) \operatorname{sinc}(t-k). $$
Émile Borel, 1897
Dans sa note Sur l'interpolation de 1897, Émile Borel énonce une version étonnamment précise du théorème d'échantillonnage : il suppose que la transformée de Fourier $\hat{f}(x)$ est à support dans $]-\frac{1}{2},\frac{1}{2}[$ et vérifie les « conditions de Dirichlet » (typiquement de classe $C^1$ par morceaux) et affirme alors que $f(t)$ est « connue sans ambiguïté » par ses valeurs en $t=0,\pm1,\pm2,...$, autrement dit, entièrement déterminée par ses échantillons $f(k)$ pour tout $k$ entier !

Le théorème d'échantillonnage... par Borel, qui utilise la notation des mathématiciens pour la transformée de Fourier, ici sous la forme de sa formule d'inversion : $\varphi(x)$ est la transformée de Fourier de $f(z)$, considérée comme une fonction entière de la variable complexe $z$.
Pour Borel, cette petite remarque anodine semble aller de soi dans le cadre de la théorie des séries de Fourier, et son raisonnement correspond exactement à celui que détaillera Shannon en 1949. Mais il ne donne pas la formule d'interpolation permettant de reconstruire $f$ à partir de ses valeurs en les entiers, alors que son article est précisément consacré à l'interpolation. Pourtant, la formule générale qu'il donne au début de son article, ce qu'il appelle la « formule d'interpolation de Lagrange » : $$ f(z)= \sum_k f(a_k)\frac{ \phi(z)}{(z-a_k)\phi'(a_k)} $$ permet de trouver $f(z)$ pour tout $z\in\mathbb{C}$ par interpolation à partir de ses valeurs en un nombre infini de points $a_k\in \mathbb{C}$ en choisissant judicieusement une fonction entière $\phi(z)$ qui s'annule en ces points. Il annonce qu'il « espère revenir prochainement sur ce sujet dans un Mémoire plus étendu » et c'est ce qu'il fait deux ans plus tard en 1899 dans son Mémoire sur les séries divergentes, où il donne bien en illustration pour $a_k=k$ la série des sinus cardinaux $$ f(z) =\frac{1}{\pi}\sum_{k\in\mathbb{Z}} \frac{\operatorname{sin} \pi z}{z-k} (-1)^k f(k) $$ et des conditions de sa convergence, sans mentionner cependant la contrainte de bande limitée en fréquence. On est donc là encore dans un contexte d'interpolation qui ne correspond pas au problème de la reconstruction après échantillonnage. Ainsi Borel est passé tout près du théorème d'échantillonnage, sans vraiment l'expliciter tout à fait !
Augustin-Louis Cauchy, 1826
On peut dire qu'Augustin-Louis Cauchy a donné dès 1826, dans son exercice de mathématiques intitulé Sur diverses relations qui existent entre les résidus des fonctions et les intégrales définies, une méthode générale qui contient le théorème d'échantillonnage comme cas particulier. Il expose en effet plusieurs exemples de sa méthode des résidus où une certaine fonction d'une variable complexe est décomposée de la façon suivante : $$ \varphi(z) = \sum \text{Rés}\bigl( \frac{\varphi(z)}{t-z}\bigr), $$ la somme des résidus portant sur les pôles de $\varphi$. Comme le fera plus tard Ogura en 1920, le théorème d'échantillonnage sur $f$ en résulte en appliquant cette méthode à $\varphi(z)=f(z)/\operatorname{sin}\pi z$. Mais Cauchy ne l'identifie pas explicitement. Il donne cependant les deux formules d'interpolation pour les fonctions sinusoïdales $\operatorname{cos} a t$ et $\operatorname{sin} a t$ (où $|a|\lt\pi$), qu'il redonnera d'ailleurs dans deux autres articles l'année suivante.
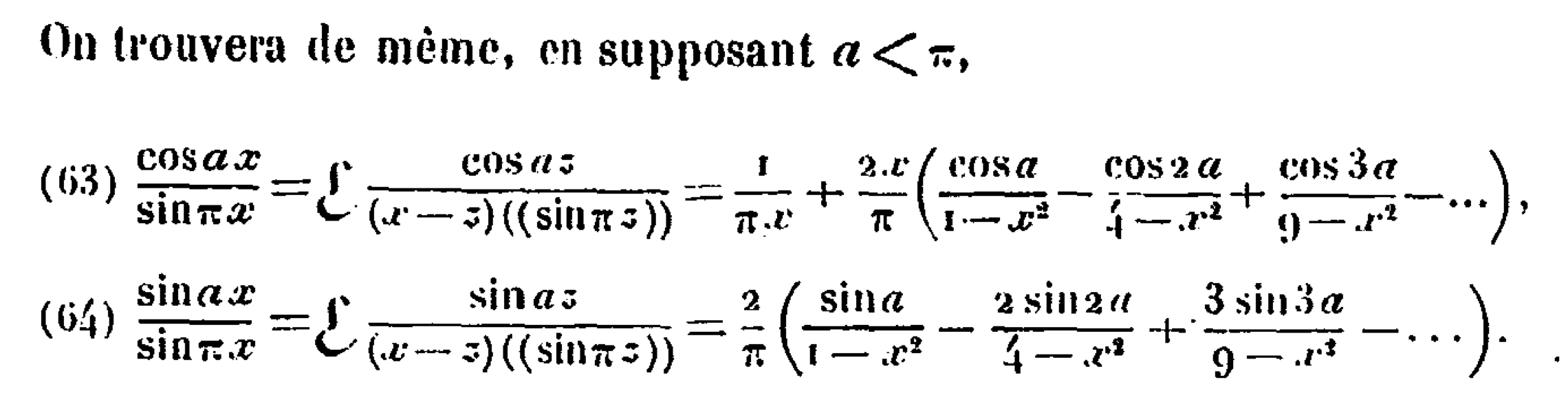
Le théorème d'« échantillonnage »... par Cauchy pour les fonctions $\operatorname{cos} a t$ et $\operatorname{sin} a t$. On peut facilement les réécrire sous la forme classique $\operatorname{cos} at=\sum_{k\in\mathbb{Z}} \operatorname{cos} at \operatorname{sinc}(t-k)$ et $\operatorname{sin} at=\sum_{k\in\mathbb{Z}} \operatorname{sin} at \operatorname{sinc}(t-k)$.
En combinant ces deux formules on obtiendrait $e^{iat}=\sum_{k\in\mathbb{Z}} e^{iak} \operatorname{sinc}(t-k)$ pour tout $|a|\lt\pi$, d'où on pourrait, en multipliant par la transformée de Fourier de $f$ en $a$ et en intégrant sur $a\in(-\pi,+\pi)$, en déduire le théorème d'échantillonnage pour toute fonction $f$ à bande limitée !
Cauchy est un peu plus explicite en 1827 où il revient sur sa Méthode pour développer des fonctions d'une ou plusieurs variables en séries composées de fonctions de même espèce, ces dernières « fonctions de même espèce » renfermant une variable qui prend des valeurs « respectivement égales aux diverses racines d'une équation transcendante », ce qu'on pourrait interpréter comme des échantillons de la fonction en question. La formule des résidus utilisée par Cauchy prend ici la forme $$ f(z) = F(z) \sum \text{Rés}\bigl( \frac{f(z)}{(t-z)F(z)}\bigr), $$ la somme des résidus porte sur les zéros de $F$. Il mentionne le cas $F(z)=\operatorname{sin} az$ (ce qui donnerait le théorème d'échantillonnage), mais là encore revient sur les mêmes formules particulières pour les fonction sinus et cosinus sans donner le cas général. Ce qu'il l'intéresse est plutôt de multiplier les exemples de formules particulières. Il exploite notamment d'autres exemples de fonctions $F(z)$ qui correspondent à des échantillonnages irréguliers, où les instants d'échantillonnage ne sont pas en progression arithmétique.
Leonhard Euler, 1783
Cauchy redonne encore les formules d'échantillonnage pour les fonctions cosinus et sinus dans son Usage du calcul des résidus pour la sommation ou la transformation des séries dont le terme général est une fonction paire du nombre qui représente le rang de ce terme de 1827, en les attribuant cette fois-ci à Leonhard Euler :
« Les formules [...] coincident avec deux équations données par Euler, dans le tome II des opuscules analytiques »
Effectivement, dans le 32e paragraphe son article intitulé Investigatio valoris integralis $\int \frac{x^{m-1} \mathrm{d}x }{1-2x^k \operatorname{cos} \theta + x^{2k}}$ a termino $x=0$ ad $x=\infty$ extensi (Recherche sur la valeur de l'intégrale $\int_0^{+\infty} \frac{x^{m-1} \mathrm{d}x }{1-2x^k \operatorname{cos} \theta + x^{2k}}$) on y trouve bien ces formules, en relation avec des développements en série représentant l'intégrale étudiée. Mais cependant, rien qui s'apparente au théorème d'échantillonnage.

La formule d'interpolation du théorème d'« échantillonnage »... par Euler pour les fonctions de cosinus et sinus, des « sommations dignes de mémoire » selon l'auteur.
Certains auteurs remontent également à Joseph-Louis Lagrange et son cours de 1795 à l'École normale de l'an III (qui n'était pas encore l'ENS), intitulé Sur l'usage des courbes dans la solution des Problèmes, où il expose sa formule d'interpolation polynomiale (uniquement avec un nombre fini de termes) qui permettrait par un passage à la limite de retrouver le théorème d'échantillonnage. On trouve également une démonstration complète de cette formule d'interpolation polynomiale par Edward Waring : Problems concerning Interpolations dès 1779. On est cependant là très loin de l'idée du théorème d'échantillonnage. D'autres auteurs ont également faussement attribué le théorème d'échantillonnage à Cauchy dans un article de 1841, à Poisson (à cause de sa formule sommatoire?), ou à Hadamard (dans un article proche de celui de Borel).

En résumé de tout cela, si l'on voulait être précis en mentionnant tous les inventeurs possibles, le théorème d'échantillonnage devrait s'appeler
théorème de Euler-Cauchy-Borel-de La Vallée Poussin-Whittaker-Ogura-Küpfmüller-Nyquist-Kotel'nikov-Raabe-Bennett-Gabor-Someya-Weston-Shannon !
Plus sérieusement, l'attribution de ce théorème suscite débat. Pour ce qui concerne les noms les plus cités :
- l'appeler « théorème de Nyquist » est sans doute une erreur historique car celui-ci n'a pas réellement considéré la problématique de l'échantillonnage, mais plutôt de la transmission de symboles sans interférences ;
- l'appeler « théorème de Shannon » est justifié dans une certaine mesure seulement, car si son article a contribué à populariser ce résultat dans le domaine de l'ingénierie, Shannon lui-même ne s'en attribue pas le mérite. L'héritage de Shannon réside plutôt dans ses théorèmes de codage en théorie de l'information, qui sont au moins aussi importants en ce qu'ils ont permis l'avènement du monde du numérique.
Si, en revanche, on veut insister sur les premiers découvreurs du théorème en étant le plus juste possible, ce travail tend à montrer qu'il faudrait surtout citer Kotel'nikov côté ingénieurs, et Ogura, dans une moindre mesure Borel, côté mathématiciens.






