La contribution d'un des premiers ordinateurs à une conjecture célèbre.
Dans un article (écrit en latin en 1778 et publié en 1802, que l'on fournit ci-dessous, pour les plus classiques de nos lecteurs), Euler conjecture, sur les entiers, le résultat suivant:
Deux cubes ne peuvent pas s'additionner pour former un cube, trois quatrièmes puissances ne peuvent pas s'additionner pour former une quatrième puissance, et, en général, la somme de ($n-1$) puissances $n$-ièmes ne peut pas être une puissance $n$-ième.
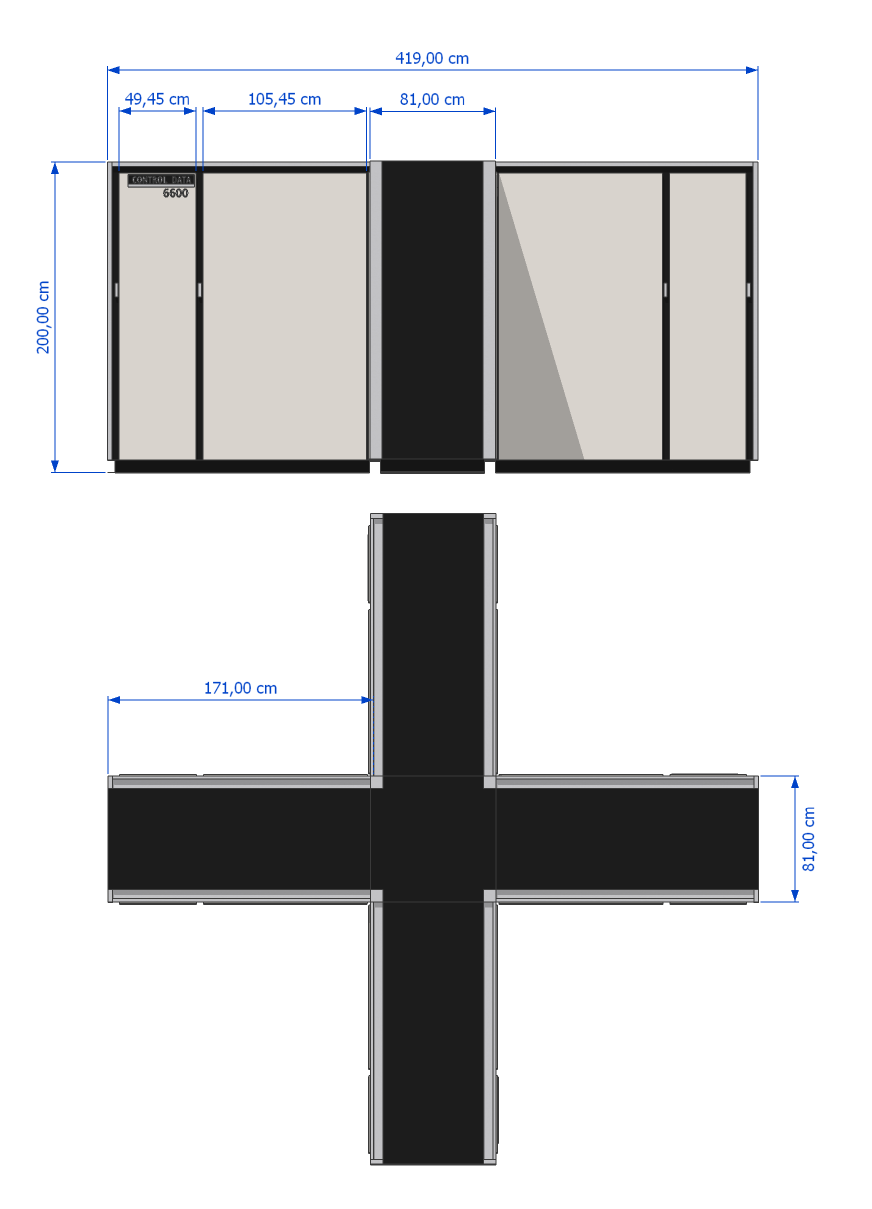
Le premier cas ($n=3$) est vrai d'après le théorème de Fermat-Wiles; en revanche, cela n'est pas vrai en général, puisque qu'en 1966, par la force brute d'un ordinateur CDC 6600 — un ordinateur de taille imposante constitué de quatre panneaux d'environ deux mètres sur deux mètres positionnés debout et formant une sorte de croix (voir figure 2) — les mathématiciens L. J. Lander et T. R. Parkin arrivent à fournir, pour $n=5$, le contre-exemple suivant: $$27^5 + 84^5 + 110^5 + 133^5 = 144^5 $$
Ce qui donnera lieu, par la même occasion, probablement au plus petit article de l'histoire des mathématiques:

Par la suite des contres-exemples ont été trouvés pour $n=4$, mais pour le moment aucun pour $n>5$...





