Le chiffrement au cœur du programme de Mathématiques Expertes.
Quels enfants ne se sont jamais amusés à échanger des messages codés ? … n’ont jamais pratiqué sans le savoir le code de César, utilisé jadis par le célèbre empereur ? Nul doute que les élèves inscrits en Maths Expertes en Terminale prendront plaisir à découvrir l’arithmétique sous-jacente aux distractions de leur jeunesse et à programmer des machines à (dé)coder, occasion inespérée de réinvestir les notions au programme 1 : congruences, calcul matriciel, théorèmes de Gauss et de Bézout, petit théorème de Fermat…
De César à Vigenère, en passant par le chiffrement affine
Le codage de César, qui consiste à déplacer les lettres d’un message à pas constant, est un cas particulier du codage affine, où $$y \equiv ax + b \; [26] $$ $x$ désignant le rang de la lettre en clair, $y$ celui de la lettre à coder et où $(a;b)$ constitue la clé de chiffrement choisie.
Une clé de chiffrement n’est valide que si le décodage est possible, c'est-à-dire si la fonction de codage constitue une bijection de l’alphabet sur lui-même. Le théorème de Gauss permet d’affirmer que c’est le cas si $a$ est premier avec $26$, et le théorème de Bézout permet d’affirmer qu’il existe alors une clé permettant le déchiffrement. En effet, si $a$ est premier avec $26$, il existe un couple $(u;v) \in \mathbb{Z}^2$ tel que $au+26v = 1$, et $u$ est donc un inverse de $a$ modulo $26$, qui vérifie $au \equiv 1 \; [26]$. De $y \equiv ax + b \; [26]$, on déduit successivement $uy \equiv aux + ub \; [26]$ et $x \equiv uy - ub \; [26]$, cette dernière égalité permettant le déchiffrement du code.
Un chiffrement affine se décode donc à l’aide d’un chiffrement affine : c’est le même algorithme et donc la même fonction informatique qui permettent le codage et le décodage. En raisonnant modulo $26$, il n’y a que $12$ valeurs possibles pour $a$ et $26$ valeurs possibles pour $b$, donc il n’existe que $312$ clés1 de chiffrement valides, ce qui est bien peu pour assurer la confidentialité des échanges !
| Lettre à coder |
| Rang de la lettre à coder : $x$ |
| Rang de la lettre codée : $y$ |
| Lettre codée |
### CHIFFREMENT AFFINE
Alphabet="ABCDEFGHIJKLMNOPQRSTUVWXYZ" # mise en mémoire de l'alphabet
def codage_affine(a,b,message):
"""
Fonction effectuant le codage affine du message
avec la clé de chiffrement (a,b)
"""
code=""
for caractere in message: # pour chaque caractère du message :
if caractere in Alphabet: # si ce caractère est dans l'alphabet, alors :
x = Alphabet.index(caractere) # on récupère l'entier correspondant à cette lettre
y = (a*x+b)%26 # on calcule y
code += Alphabet[y] # on complète le code avec la lettre correspondant à y
else: # sinon :
code += " " # on complète le code avec un espace
return code # on renvoie le message codé
def inverse_cle(a,b):
"""
Fonction renvoyant (si elle existe) la clé de déchiffrement (u,v)
associée à la clé de chiffrement (a,b)
"""
for u in range(26): # pour chaque entier u jusqu'à 25 :
if (a*u)%26==1: # si u est inverse de a modulo 26 alors:
return u,(-b*u)%26 # on renvoie la clé composée de u
# et du reste de la division euclidienne de -bu par 26
Blaise de Vigenère (1523-1596) propose une version dérivée du chiffrement affine, qui consiste à utiliser un mot-clé à la place de la formule affine pour déterminer le décalage : $$y \equiv x+c \; [26]$$ où $c$ est le rang de la lettre du mot clé correspondant à l'emplacement de la lettre à coder.
De cette façon, le codage d’une lettre dépend de sa place dans le message, ce qui rend la méthode bien plus robuste, résistante notamment aux méthodes d’analyse des fréquences d’apparition des lettres, quoique des méthodes de piratage de ce code aient été publiées depuis1.
Évidemment, si le mot clé de chiffrement est connu, le déchiffrement se fait sans difficulté puisque $x \equiv y-c \; [26]$.
| Message à coder |
| Rang de la lettre à coder : $x$ |
| Répétition de la clé |
| Rang de la lettre de la clé : $c$ |
| Rang de la lettre codée : $y$ |
| Message codé |
### CHIFFREMENT DE VIGENERE
Alphabet="ABCDEFGHIJKLMNOPQRSTUVWXYZ" # mise en mémoire de l'alphabet
def codage_Vigenere(message,cle,sens=True):
"""
Fonction effectuant le codage de Vigenere du message avec la cle
(le décodage de Vigenere si sens vaut False)
"""
l_cle = len(cle) # longueur de la clé
j=0 # on initialise rang de la lettre de la clé utilisée
code=""
for caractere in message: # pour chaque caractère du message :
if caractere in Alphabet: # si c'est une lettre de l'alphabet :
x = Alphabet.index(caractere) # on stocke dans x le rang de cette lettre
c = Alphabet.index(cle[j]) # on stocke dans c le rang de la lettre de la clé
y = (x+ (1 if sens else -1)*c ) %26 # on calcule le rang y de la lettre codée correspondante
code += Alphabet[y] # on complète le code avec la lettre de rang y
j = (j+1) %l_cle # on avance d'un rang dans la clé
else: # sinon:
code += " " # on complète le code avec un espace
return code # on renvoie le code
Les apports de Hill
Lester S. Hill (1891-1961) a perfectionné le principe du chiffrement affine en proposant un codage matriciel par blocs, qui peut être abordé par les élèves de Terminale Math Expertes puisque les bases du calcul matriciel sont au programme.
Étant donné une matrice carrée $H$ d'ordre $n$ à coefficients entiers, il s’agit de coder le message par blocs de $n$ caractères, de telle sorte que $$Y \equiv H X \; [26]$$ où $X$ est la matrice colonne dont les coefficients correspondent aux caractères du bloc à coder et $Y$ à ceux du bloc codé.
$H$ constitue la clé du chiffrement, et comme dans le cas du chiffrement affine, cette clé n'est valide que si le message peut être décodé sans ambiguïté, ce qui équivaut à dire que la matrice $H$ est inversible dans $\mathcal{M}_n (\mathbb{Z}/26\mathbb{Z})$.
$H \in \mathcal{M}_n (\mathbb{Z}/26\mathbb{Z})$ inversible $\Longleftrightarrow \mathrm{det}{\left(H\right)}$ est inversible dans $\mathbb{Z}/26\mathbb{Z} \Longleftrightarrow \mathrm{det}{\left(H\right)}$ est premier avec $26$.
Dans le cas où $d=\mathrm{det}(H)$ est premier avec $26$, on note $u$ son inverse modulo $26$ et $D=u \times {}^t \mathrm{com}(H)$.
Alors $DH = u \times {}^t \mathrm{com}(H) H = u \times d I_n \equiv I_n \; [26]$ et $D$ est donc la matrice inverse de $H$ dans $\mathcal{M}_n (\mathbb{Z}/26\mathbb{Z})$, ce qui permet d'établir :
$$Y \equiv HX \; [26] \Longleftrightarrow X \equiv DY \; [26]$$
Le chiffrement matriciel de Hill de clé $H$ se décode donc à l’aide du chiffrement matriciel de Hill de clé $D$ où $D$ est la matrice inverse de $H$ dans $\mathcal{M}_n\ (\mathbb{Z}/26\mathbb{Z})$. On peut également établir que, modulo $26$, il y a $448508$ matrices de chiffrement valides d’ordre $2$.
| Message à coder |
| Colonne à coder : $X$ |
| Colonne codée : $Y$ |
| Message codé |
### CHIFFREMENT DE HILL
import numpy as np
Alphabet="ABCDEFGHIJKLMNOPQRSTUVWXYZ" # mise en mémoire de l'alphabet
def codage_Hill(message,H):
"""
fonction réalisant le codage du message
à l'aide de la matrice de chiffrement H
"""
code=""
if len(message)%2 !=0: # s'il n'y a pas un nombre pair de lettres :
message += "A" # on complète le message avec un A
for k in range(len(message)//2): # pour chaque couple de lettres du message :
X = np.array([[ Alphabet.index(message[2*k])], # on crée la matrice X
[ Alphabet.index(message[2*k+1]) ]])
Y = np.dot( H , X ) %26 # on calcule la matrice Y
code += Alphabet[Y[0][0]]+Alphabet[Y[1][0]] # on complète le code avec les deux lettres obtenues
return code # on renvoie le message codé
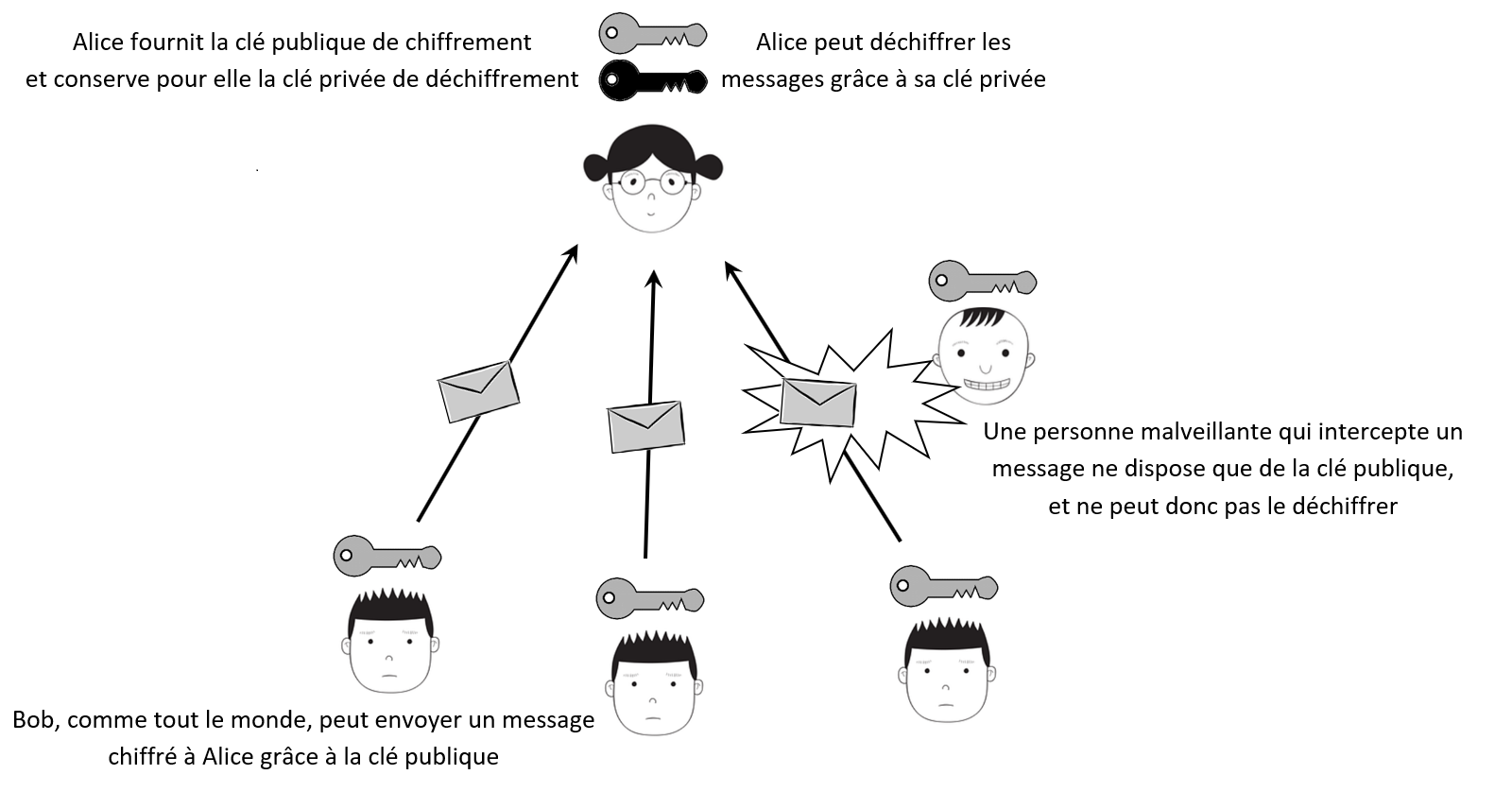
Vers un chiffrement asymétrique : le RSA
Au-delà de la nécessité d’avoir un grand nombre de clés distinctes, le souci de confidentialité impose de pouvoir fournir la clé de chiffrement à toutes les personnes susceptibles de nous envoyer un message, sans que celles-ci soient en mesure elles-mêmes de décoder ces messages. Les méthodes de chiffrement exposées précédemment ne permettent pas de répondre à cette contrainte, car tout mathématicien qui se respecte disposant de la clé de chiffrement sera à même de construire la clé de déchiffrement. Il faut donc, pour cela, mettre en œuvre une méthode de chiffrement asymétrique.
Le RSA1 est une méthode de cryptographie qui permet de répondre à cette problématique : À partir de deux nombres premiers distincts $p$ et $q$, on construit les entiers $n=pq$ ; $m=(p-1)(q-1)$ et on choisit un entier $c$ strictement inférieur à $m$ et premier avec $m$. La formule de chiffrement qui permet d'associer à un message une liste d'entiers est $$y \equiv x^c \; [n]$$ où le couple $(n;c)$ constitue la clé publique de chiffrement.
| Message à coder |
| Rang de la lettre à coder : $x$ |
| Entier codé : $y$ |
Construisons maintenant la clé privée de déchiffrement : On note $d$ l'inverse de $c$ modulo $m$, vérifiant $1 \leq d < m$ et $cd \equiv 1 \; [m]$. Il existe donc un entier $k$ positif tel que $cd=1+km$.
On va établir que pour tout entier $x$, on a $x^{cd} \equiv x \; [n]$. Ce résultat découle d'un cas particulier du théorème d'Euler, portant sur l'indicatrice d'Euler, mais il peut également être démontré à grand renfort du petit théorème de Fermat et de conséquences du théorème de Gauss, au programme de Terminale Mathématiques Expertes.
Les seuls diviseurs de $n=pq$ étant $1$ ; $p$ ; $q$ et $pq$, on raisonne par disjonction des cas sur la valeur du $PGCD$ de $x$ et $n$ :
- Si $PGCD(x;n)=1$ :
Comme $p$ divise $n$, il ne peut pas diviser $x$ et n'apparaît donc pas dans la décomposition en produits de facteurs premiers de $x$ et donc pas non plus dans celle de $x^{q-1}$. En appliquant le petit théorème de Fermat1 à $p$ et $x^{q-1}$, il vient $x^{(q-1)(p-1)} \equiv 1 \; [p]$. En inversant les rôles de $p$ et $q$ dans le raisonnement, on peut également établir que $x^{(q-1)(p-1)} \equiv 1 \; [q]$.
$p$ et $q$ étant deux nombres premiers distincts qui divisent $x^{(p-1)(q-1)}-1$, leur produit $pq$ divise aussi ce nombre. On a donc $x^{(q-1)(p-1)} \equiv 1 \; [pq]$, c'est à dire $x^m \equiv 1 \; [n]$.
Finalement, on a $x^{cd} = x^{km+1} = (x^m)^k x \equiv x \; [n]$.
- Si $PGCD(x;n)=p$ :
$q$ étant un diviseur de $n$, il ne divise pas $x$ et le petit théorème de Fermat donne $x^{q-1} \equiv 1 \; [q]$. On en déduit que : $$x^{cd}=x^{km+1}=x^{k(q-1)(p-1)+1}=(x^{q-1})^{k(p-1)}x \equiv x \; [q]$$ D'autre part $p$ est un diviseur de $x$ donc comme $cd \geq 1$, $p$ divise aussi $x^{cd}-x$.
$p$ et $q$ étant deux nombres premiers distincts qui divisent $x^{cd}-x$, leur produit $n=pq$ divise aussi ce nombre, ce qui donne $x^{cd} \equiv x \; [n]$.
Le cas où $PGCD(x;n)=q$ se traite de la même façon, par symétrie des rôles de $p$ et $q$.
- Si $PGCD(x;n)=pq$ alors $n=pq$ divise $x$ et donc $x \equiv 0 \; [n]$, d'où on déduit immédiatement $x^{cd} \equiv 0 \; [n]$ et $x^{cd} \equiv x \; [n]$.
Dans tous les cas $x^{cd} \equiv x \; [n]$, ce qui permet d'expliciter la méthode de décodage : $$y \equiv x^c \; [n] \Longrightarrow y^d \equiv x^{cd} \; [n] \Longrightarrow x \equiv y^d \; [n]$$
Pour décoder le message, il convient de pouvoir construire $d$ et donc de connaître $m$, et comme $m=(p-1)(q-1)$ cela nécessite la connaissance des nombres premiers $p$ et $q$ initiaux. Leur produit $n$ étant fourni dans la clé publique, la sécurité du codage RSA réside dans la difficulté (idéalement l'impossibilité) de redécomposer cette valeur $n$ en produit de facteurs premiers.
Des valeurs modestes de $p$ et $q$ peuvent évidemment facilement être retrouvées, c'est pourquoi la cryptographie RSA actuelle est basée sur des nombres premiers gigantesques qui peuvent être composés de plus de $200$ chiffres ! Ainsi, imaginé en 1977, le RSA résiste encore aujourd'hui aux attaques2 et est couramment utilisé dans les échanges internet et/ou commerciaux.
| Entier codé : $y$ |
| Rang de la lettre décodée : $x$ |
| Message décodé |
### CHIFFREMENT RSA
Alphabet="ABCDEFGHIJKLMNOPQRSTUVWXYZ" # mise en mémoire de l'alphabet
def chiffrage(message):
"""
Fonction qui renvoie la liste des valeurs correspondantes aux caractères du message
(A->0 , B->1 , ...)
"""
return [ Alphabet.index(caractere) for caractere in message ]
def chiffrement_RSA(n,c,liste_nombres):
"""
Fonction effectuant le codage RSA de la liste de valeurs avec la clé publique (n,c)
"""
code = []
for x in liste_nombres: # pour chaque valeur x de la liste donnée
y = x**c %n # on calcule y correspondant à x
code.append(y) # on complète la liste de valeurs avec y
return code # on renvoie le code
def inverse(m,c):
"""
Fonction qui renvoie (s’il existe) l’inverse de c modulo m
"""
for d in range(m): # on parcourt les entiers d jusqu'à m-1 :
if (c*d)%m==1 : return d # si d est inverse de c modulo m : on renvoie d
def dechiffre_RSA(p,q,c,code):
"""
Fonction effectuant le décodage RSA du code à partir de c et des nombres premiers p et q
"""
n = p*q ; m = (p-1)*(q-1) ; d = inverse(m,c) # calculs de n, m et d
return [y**d %n for y in code] # on renvoie la liste des valeurs correspondantes aux valeurs y du code
def lettrage(code):
"""
Fonction qui convertit une liste de valeurs (comprises entre 0 et 25) en chaine de caractères
(0->A , 1->B , ...)
"""
message = ""
for y in liste: # pour chaque valeur de la liste :
message += Alphabet[y] # on ajoute au message la lettre correspondante
return message # on renvoie le message
Pour faire découvrir les notions détaillées dans cet article à des élèves de Terminale Math Expertes, vous trouverez ici trois activités de programmation Python sur le chiffrement, accessibles directement en ligne sans téléchargement préalable.
Pour plus de détails, on pourra voir également le livre Codage et Cryptographie de Joan Gómez 1.
Les passionnés de cryptographie pourront consulter cet autre article publié sur Culture Math : Le chiffrement de Rabin de Robert Cabane.
Documents à télécharger